Главная

Задача 1. Расчет плоских статически неопределимых рам методом перемещений

Для заданной статически неопределимой рамы (рис.1) с выбранными из табл.1 размерами и нагрузкой построить эпюры изгибающих моментов, поперечных и продольных сил.

Таблица 1

Номер cтроки	Номер схемы по рис.1	l1, м	l2, м	h1, м	h2, м	q, кН/м	P1, кН	P2, кН	P3, кН	I1/I2
1	1	4	10	3	11	1,1	4	0	0	0,5
2	2	5	11	9	8	1,3	0	4	0	2,0
3	3	6	8	4	5	0,8	0	0	4	0,6
4	4	3	12	7	6	1,7	5	0	0	1,5
5	5	7	5	5	3	1,8	0	5	0	0,3
6	6	12	4	6	4	1,2	0	0	5	3,0
7	7	10	3	8	9	0,9	6	0	0	0,8
8	8	8	7	12	10	1,4	0	6	0	1,3
9	9	9	6	11	7	1,0	0	0	6	4,0
10	10	11	9	10	6	1,5	7	0	0	0,2
11	11	6	8	5	6	1,6	0	7	0	0,4
12	12	7	5	11	10	1,3	0	0	7	1,8
13	13	12	11	7	9	1,1	7	0	0	0,9
14	14	4	3	6	4	1,5	0	6	0	1,0
15	15	10	9	13	8	1,0	0	0	6	1,2
16	16	8	13	10	12	1,4	6	0	0	1,4
17	17	6	4	9	11	0,9	0	5	0	1,6
18	18	9	7	4	5	1,2	0	0	5	1,9
19	19	11	10	8	7	1,8	5	0	0	2,5
20	20	5	6	12	13	1,7	0	4	0	2,2
21	1	7	5	5	3	1,8	0	5	0	0,3
22	2	12	4	6	4	1,2	0	0	5	3,0
23	3	10	3	8	9	0,9	6	0	0	0,8
24	4	8	7	12	10	1,4	0	6	0	1,3
25	5	9	6	11	7	1,0	0	0	6	4,0
26	6	11	9	10	6	1,5	7	0	0	0,2
27	7	6	8	5	6	1,6	0	7	0	0,4
28	8	7	5	11	10	1,3	0	0	7	1,8
29	9	12	11	7	9	1,1	7	0	0	0,9
30	10	12	11	7	9	1,1	7	0	0	0,9
31	11	4	3	6	4	1,5	0	6	0	1,0
32	12	10	9	13	8	1,0	0	0	6	1,2
33	13	8	13	10	12	1,4	6	0	0	1,4
34	14	6	4	9	11	0,9	0	5	0	1,6
35	15	9	7	4	5	1,2	0	0	5	1,9
36	16	11	10	8	7	1,8	5	0	0	2,5
	в	а	г	б	а	г	б	в	а	б

Примечание: I₁ – момент инерции ригеля, I₂ – момент инерции стойки.

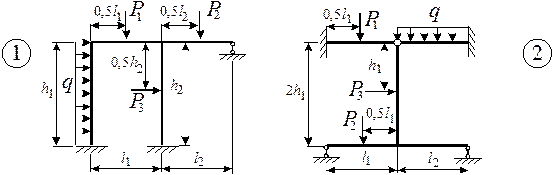
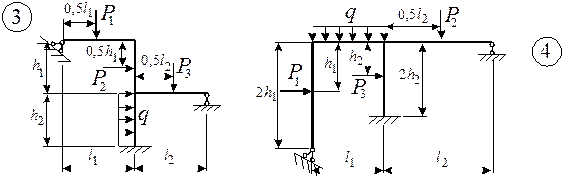
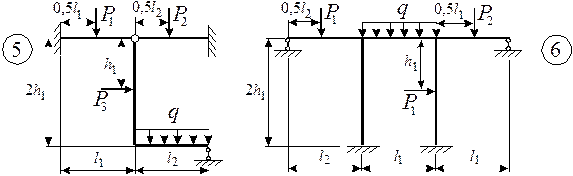
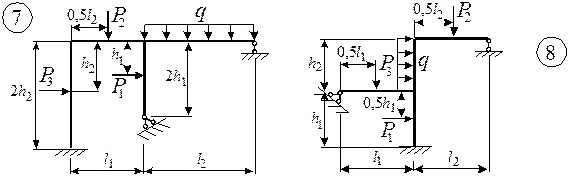
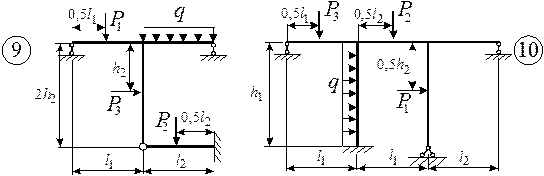
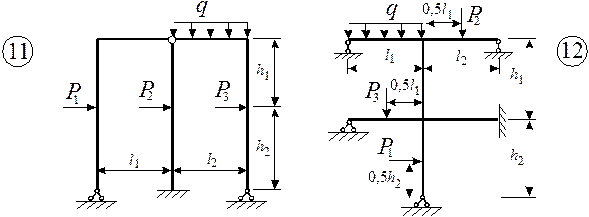
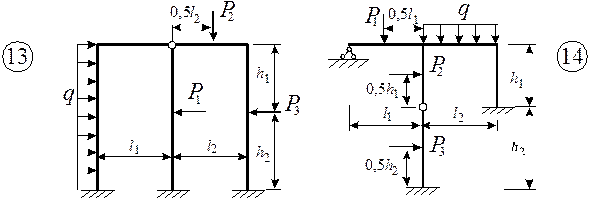
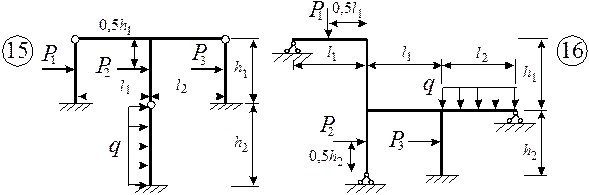
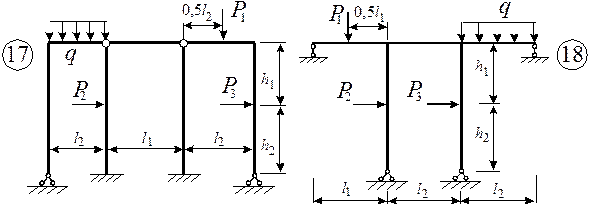
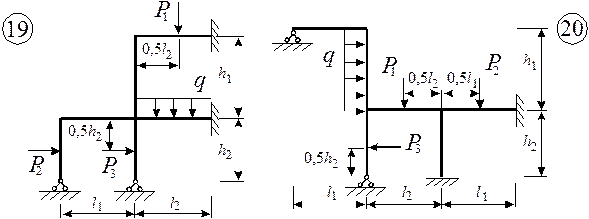
Рис.1

Пояснения к решению задачи

При выборе основной системы метода перемещений необходимо учитывать, что линейные связи должны быть поставлены не только по направлению возможных линейных перемещений, но и для устранения мгновенной изменяемости системы, образованной после постановки шарниров во все узлы (включая опорные).

Прежде чем приступать к подсчету коэффициентов канонических уравнений, необходимо значения ординат на всех единичных эпюрах выразить через какую-либо одну жесткость (EI₁ или EI₂). Удобно также перейти к погонным жесткостям стержней i=EI/l. При определении коэффициентов следует внимательно следить за их знаками.

Задача 2. Расчет плоских статически неопределимых рам методом сил и методом перемещений

Для рамы (рис. 2) с выбранными по шифру из табл. 2 размерами и нагрузкой требуется:

1) выполнить расчет рамы с использованием метода сил, построить эпюры изгибающих моментов, поперечных и продольных сил;

2) выполнить расчет рамы с использованием метода перемещений, построить эпюру изгибающих моментов и сравнить с результатами предыдущего расчета.

Таблица 2

Номер cтроки	Номер схемы по рис.2	b, м	h, м	q1, кН/м	q2, кН/м	F1, кН	F2, кН	I1/I2
1	1	3,0	6,0	2	0	8	0	1:2
2	2	3,5	7,2	0	2	0	5	2:3
3	3	4,0	8,1	4	0	6	0	1:3
4	4	4,5	9,0	0	4	0	8	3:2
5	5	5,0	5,4	6	0	7	0	2:1
6	6	3,0	7,5	0	6	0	6	3:1
7	7	3,5	8,7	4	0	5	0	1:2
8	8	4,0	6,3	0	4	0	7	3:2
9	9	4,5	7,8	6	0	8	0	2:1
10	0	5,0	9,6	0	6	0	5	1:3
11	1	3,0	6,0	2	0	8	0	1:2
12	2	3,5	7,2	0	2	0	5	2:3
13	3	4,0	8,1	4	0	6	0	1:3
14	4	4,5	9,0	0	4	0	8	3:2
15	5	5,0	5,4	6	0	7	0	2:1
16	6	3,0	7,5	0	6	0	6	3:1
17	7	3,5	8,7	4	0	5	0	1:2
18	8	4,0	6,3	0	4	0	7	3:2
19	9	4,5	7,8	6	0	8	0	2:1
20	0	5,0	9,6	0	6	0	5	1:3
21	1	3,0	6,0	2	0	8	0	1:2
22	2	3,5	7,2	0	2	0	5	2:3
23	3	4,0	8,1	4	0	6	0	1:3
24	4	4,5	9,0	0	4	0	8	3:2
25	5	5,0	5,4	6	0	7	0	2:1
26	6	3,0	7,5	0	6	0	6	3:1
27	7	3,5	8,7	4	0	5	0	1:2
28	8	4,0	6,3	0	4	0	7	3:2
29	9	4,5	7,8	6	0	8	0	2:1
30	0	5,0	9,6	0	6	0	5	1:3
31	1	3,0	6,0	2	0	8	0	1:2
32	2	3,5	7,2	0	2	0	5	2:3
33	3	4,0	8,1	4	0	6	0	1:3
34	4	4,5	9,0	0	4	0	8	3:2
35	5	5,0	5,4	6	0	7	0	2:1
36	6	3,0	7,5	0	6	0	6	3:1
	в	а	г	г	а	б	в	б

Примечание: I₁ – момент инерции ригеля, I₂ – момент инерции стойки.

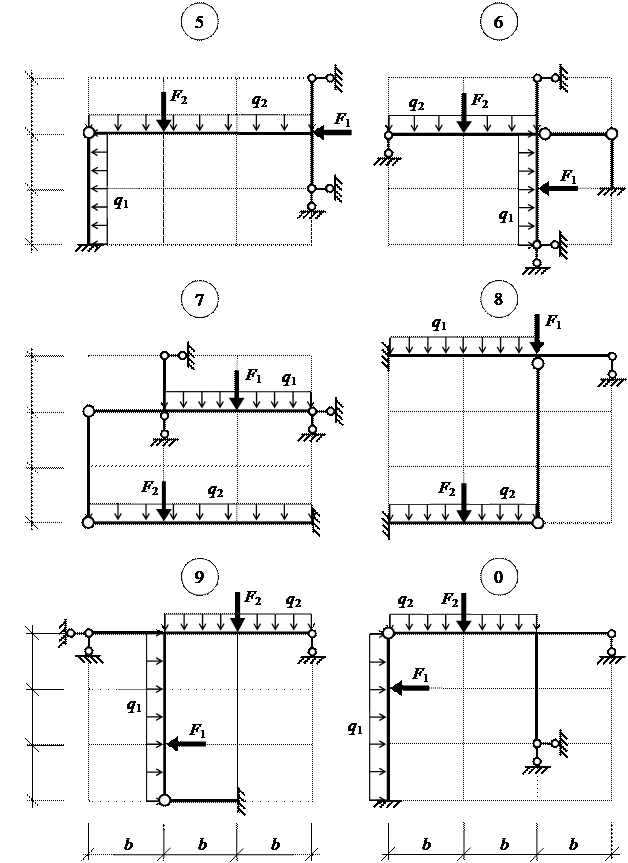
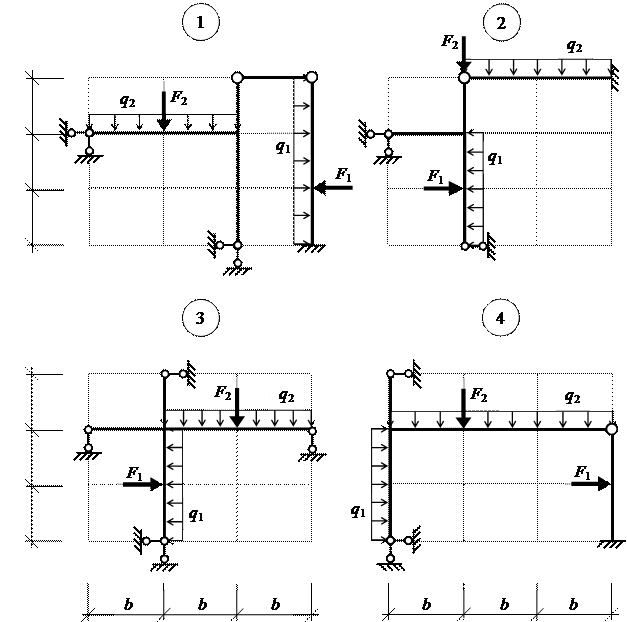
Рис.2

Пояснения к решению задачи

Порядок расчета статически неопределимой рамы методом сил:

1. Определяется число «лишних» неизвестных (равное степени статической неопределимости рамы) и выбирается основная система (ОС) метода сил. Желательно, чтобы выбранная ОС была проста для дальнейших расчетов. Например, если при отбрасывании связей (включая «разрезание» рамы по шарнирам или иным внутренним связям) заданная рама распадается на несколько простых рам или балок, являющихся статически определимыми и геометрически неизменяемыми системами, то полученная таким образом ОС будет наиболее эффективна.

2. Строятся грузовая и единичные эпюры изгибающих моментов.

3. Определяются коэффициенты и свободные члены канонических уравнений (единичные δ_ij и грузовые ∆_iF перемещения в ОС): где – единичная эпюра (от X_i = 1), M_F – эпюра изгибающих моментов от заданной нагрузки, EI – жесткость сечения. При «перемножении» эпюр следует пользоваться способами Верещагина или Симпсона.

4. Выполняется проверка коэффициентов и свободных членов: где – суммарная единичная эпюра. В результате решения системы канонических уравнений определяются значения неизвестных метода сил: X₁, X₂, …, X_i, … .

5. Строится окончательная эпюра изгибающих моментов: . Выполняется кинематическая проверка – путем «умножения» M на суммарную эпюру , результат умножения должен быть равен нулю (или быть близким к нулю): .

6. Строятся эпюры поперечных и продольных сил. Ординаты эпюры Q определяются по формуле: . Эпюра N строится по эпюре Q путем вырезания узлов, начиная с узла, в котором число неизвестных продольных сил не превышает двух. При вырезании каждого узла необходимо учитывать, что положительная поперечная сила вращает узел по ходу часовой стрелки, а отрицательная – против часовой стрелки.

7. После построения всех окончательных эпюр выполняется статическая проверка расчета – путем проверки равновесия всей рамы: ΣF_x = 0; ΣF_y = 0; ΣM = 0.

Порядок расчета статически неопределимой рамы методом перемещений:

1. Определяется число неизвестных метода перемещений (равное степени кинематической неопределимости рамы) и выбирается основная система метода перемещений. В основной системе связи должны быть поставлены не только по направлению возможных линейных перемещений, но и для устранения угловых перемещений.

2. Строятся грузовая и единичные эпюры изгибающих моментов, при этом используются таблицы реакций, имеющиеся в учебниках.

3. Определяются коэффициенты канонических уравнений – единичные r_ij и грузовые R_ij реакции в ОС, при этом значения ординат на всех единичных эпюрах должны быть выражены через какую-либо одну жесткость (EI₁ или EI₂). При определении коэффициентов следует внимательно следить за их знаками, а также использовать теорему о взаимности реакций.

4. Выполняется проверка коэффициентов канонических уравнений: где – грузовая эпюра изгибающих моментов в основной системе метода сил. В результате решения системы канонических уравнений определяются значения неизвестных метода перемещений: Z₁, Z₂, …, Z_i. Окончательная эпюра изгибающих моментов строится путем суммирования грузовой эпюры с эпюрами моментов от Z_i: . Суммирование эпюр рекомендуется производить по характерным точкам. Эпюры поперечных и продольных сил могут быть построены по эпюре моментов так же, как и при расчете рамы методом сил.

Задача 4. Расчет плоских статически неопределимых рам методом перемещений

Для заданной статически неопределимой рамы (рис.3), с выбранными по шифру из таблицы 3 размерами и нагрузкой, требуется построить эпюры изгибающих моментов, поперечных и продольных сил.

Таблица 3

Номер cтроки	Номер схемы по рис.3	ℓ1, м	ℓ2, м	h1, м	h2, м	P1, кН	P2, кН	I1/I2
1	1	4	6	3	5	4	2	1:2
2	2	5	5	4	4	5	3	2:1
3	3	6	4	5	5	4	3	2:3
4	4	3	3	9	6	5	4	3:2
5	5	7	8	6	6	3	5	1:3
6	6	8	7	7	7	2	4	3:1
7	7	9	10	8	6	6	3	3:4
8	8	10	9	2	8	3	4	4:3
9	9	12	2	12	9	7	6	4:1
10	0	2	12	10	7	7	2	1:4
11	1	4	6	3	5	4	2	1:2
12	2	5	5	4	4	5	3	2:1
13	3	6	4	5	5	4	3	2:3
14	4	3	3	9	6	5	4	3:2
15	5	7	8	6	6	3	5	1:3
16	6	8	7	7	7	2	4	3:1
17	7	9	10	8	6	6	3	3:4
18	8	10	9	2	8	3	4	4:3
19	9	12	2	12	9	7	6	4:1
20	0	2	12	10	7	7	2	1:4
21	1	4	6	3	5	4	2	1:2
22	2	5	5	4	4	5	3	2:1
23	3	6	4	5	5	4	3	2:3
24	4	3	3	9	6	5	4	3:2
25	5	7	8	6	6	3	5	1:3
	в	а		г	а	б	в	б

Примечание: EI₁ – изгибная жесткость ригеля, EI₂ – изгибная жесткость стойки.

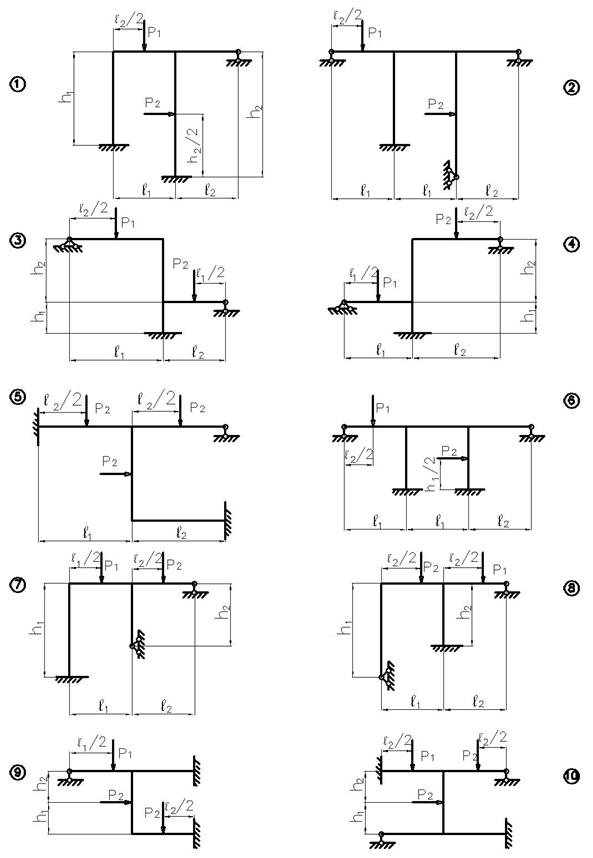
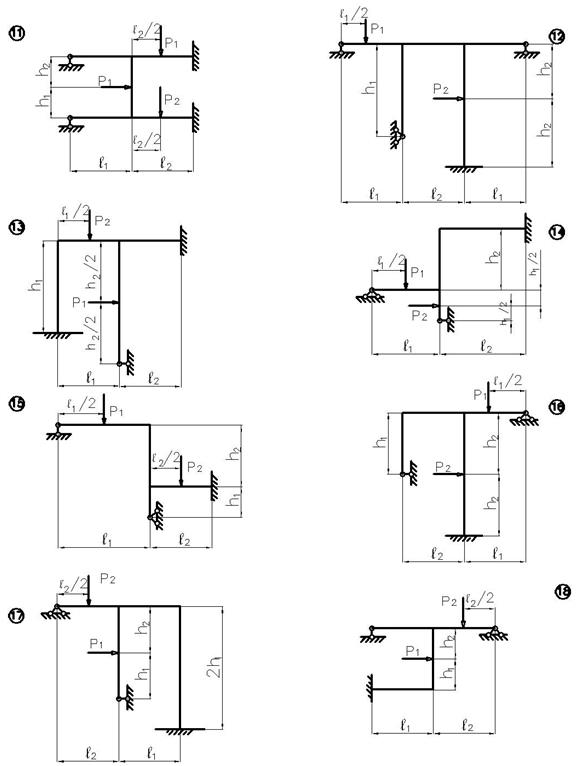
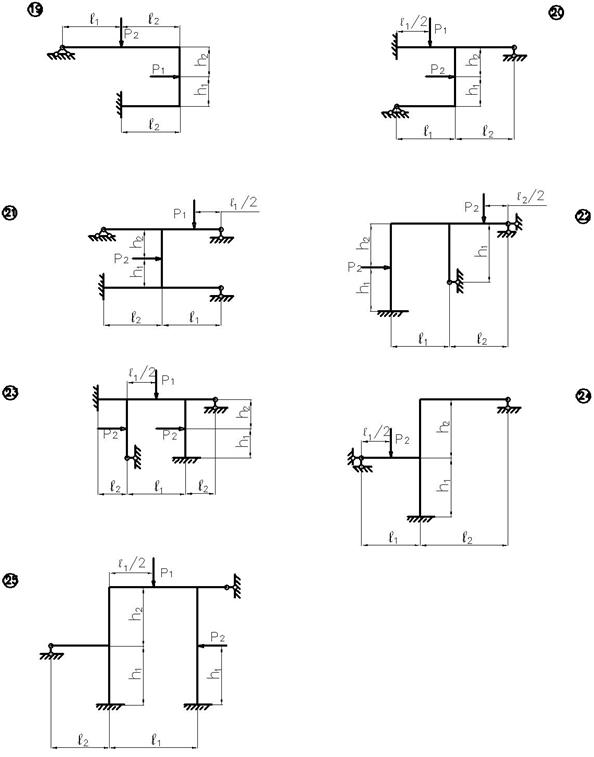
Рис.3

Задача 4. Расчет плоских статически неопределимых рам методом перемещений

Для заданной рамы (рис. 4) с выбранными по шифру из табл. 4 размерами и нагрузкой требуется:

1) раскрыть степень кинематической неопределимости рамы, построить эпюры M, Q и N;

2) произвести проверку правильности построения эпюр.

Таблица 4

Номер cтроки	Номер схемы по рис.4	l, м	h, м	q1, кН/м	q2, кН/м	P1, кН	P2, кН	I1/I2
1	1	6	6	30	0	40	0	1:2
2	2	8	8	50	30	0	0	2:3
3	3	10	8	20	0	0	40	1:3
4	4	4	4	10	0	50	0	3:2
5	5	10	8	40	20	0	50	2:1
6	6	8	6	70	0	0	60	3:1
7	7	6	4	50	20	60	0	1:2
8	8	4	8	40	0	0	70	3:2
9	9	4	7	30	0	0	50	2:1
10	10	6	4	20	0	30	0	1:3
11	11	6	6	30	0	40	0	1:2
12	12	8	8	50	30	0	0	2:3
13	13	10	8	20	0	0	40	1:3
14	14	4	4	10	0	50	0	3:2
15	15	10	8	40	20	0	50	2:1
16	16	8	6	70	0	0	60	3:1
17	17	6	4	50	20	60	0	1:2
18	18	4	8	40	0	0	70	3:2
19	19	4	7	30	0	0	50	2:1
20	20	6	4	20	0	30	0	1:3
21	21	6	6	30	0	40	0	1:2
22	22	8	8	50	30	0	0	2:3
23	23	10	8	20	0	0	40	1:3
24	24	4	4	10	0	50	0	3:2
25	25	10	8	40	20	0	50	2:1
26	26	8	6	70	0	0	60	3:1
27	1	6	4	50	20	60	0	1:2
28	2	4	8	40	0	0	70	3:2
29	3	4	7	30	0	0	50	2:1
30	4	6	4	20	0	30	0	1:3
31	5	6	6	30	0	40	0	1:2
32	6	8	8	50	30	0	0	2:3
33	7	10	8	20	0	0	40	1:3
34	8	4	4	10	0	50	0	3:2
35	9	10	8	40	20	0	50	2:1
36	10	8	6	70	0	0	60	3:1
	а	а	г	б	а	б	в	а

Примечание: I₁ – момент инерции вертикальных стержней,

I₂ – момент инерции горизонтальных и наклонных стержней.

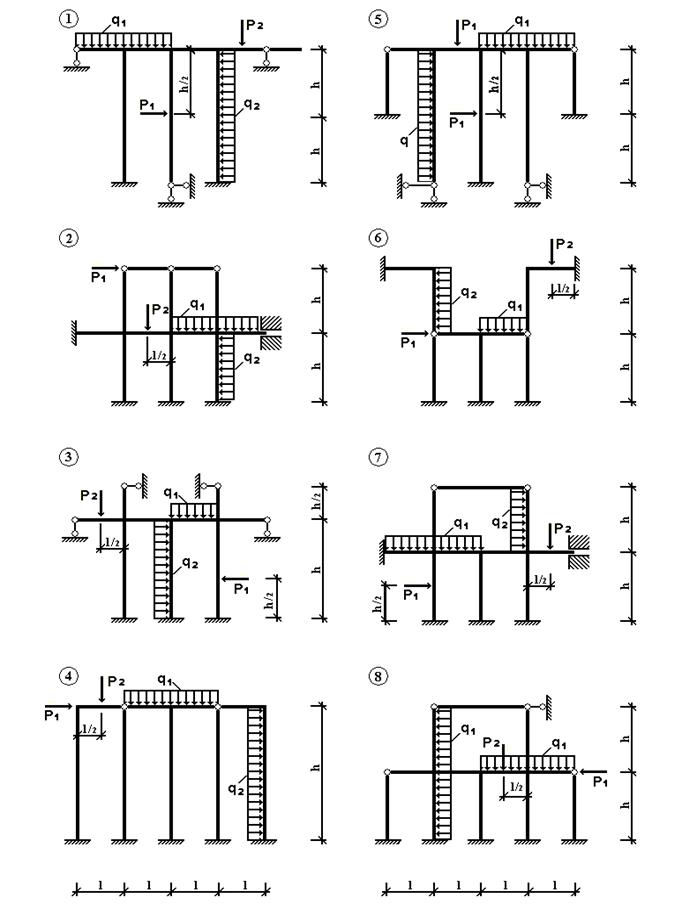
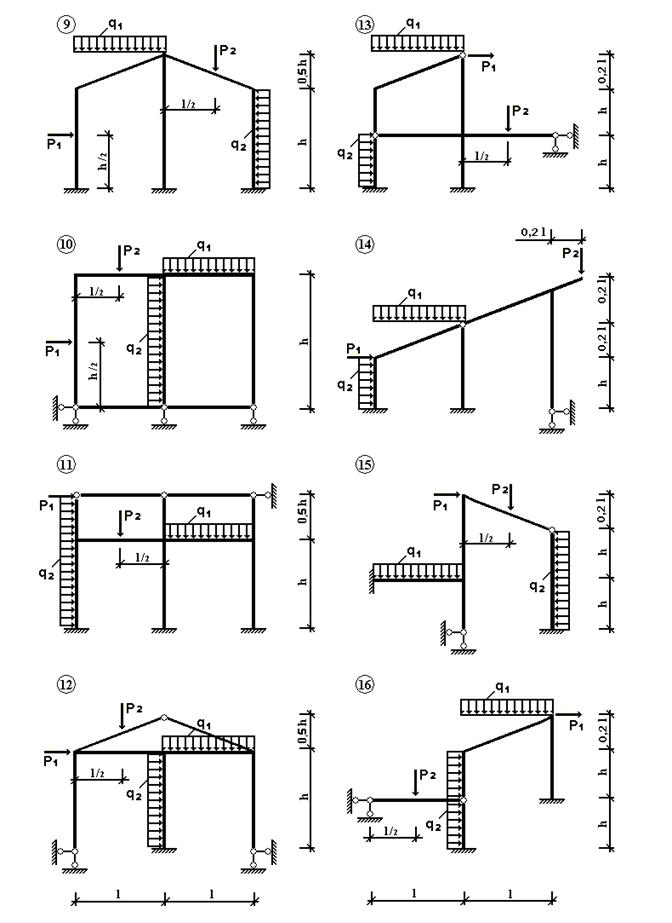
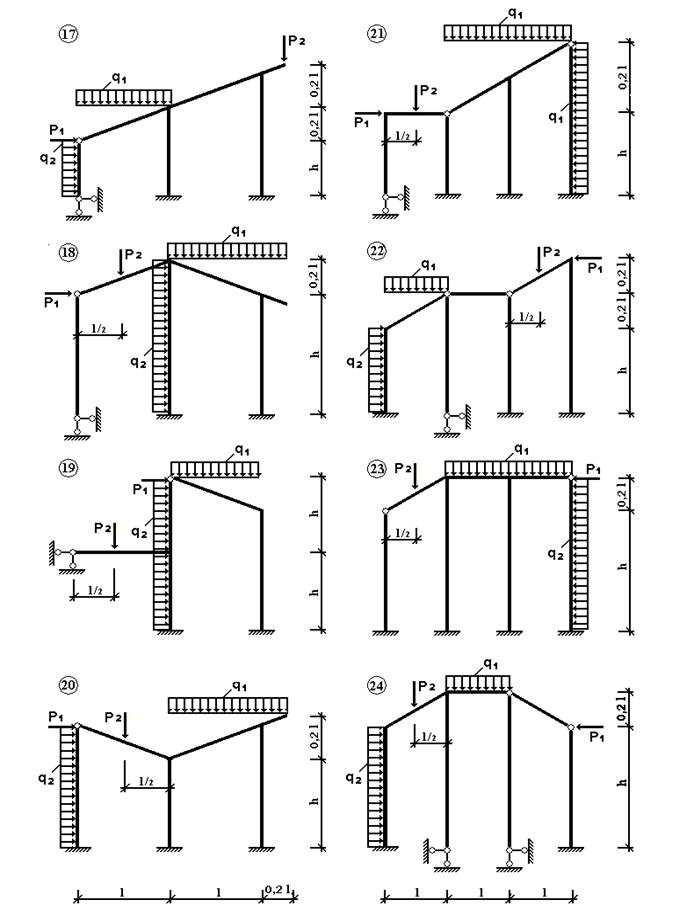
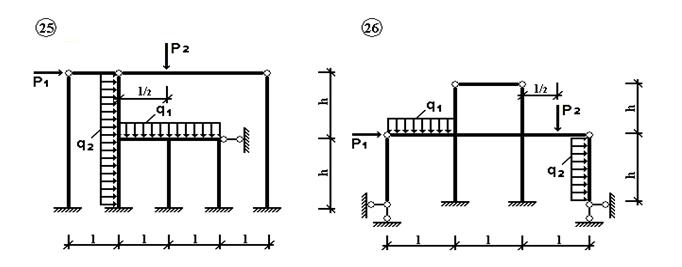
Рис.4

Пояснения к решению задачи

Метод перемещений наряду с методом сил является также точным методом.

В методе перемещений в качестве основных неизвестных принимаются характерные перемещения системы – перемещения ее узлов. Узлы – места сопряжения стержней, как правило, бывают шарнирными или жесткими. Шарнирный узел может иметь линейное перемещение, которое можно разложить на вертикальную и горизонтальную составляющие. Жесткий узел, кроме линейных перемещений может получить и угловое перемещение. Жестким считается узел, в котором не менее двух стержней соединены между собой жестко. Полагается, что перемещения узлов малы и происходят за счет изгибных деформаций стержней системы. Степень кинематической неопределимости системы подсчитывается по формуле

n = n_y + n_л, (1)

где n_у – число неизвестных углов поворота, равное числу жестких узлов рамы;

n_л – число неизвестных линейных смещений узлов, равное степени геометрической неизменяемости системы, полученной из заданной путем введения во все жесткие узлы полных шарниров (включая опоры).

После определения количества неизвестных n следует приступить к выбору основной системы. Последняя при расчете рам методом перемещений получается из заданной введением во все «жесткие» узлы защемлений, препятствующих их повороту. Кроме того, необходимо закрепить систему достаточным количеством стержней, препятствующих линейному смещению узлов. Общее число закреплений укажет на число неизвестных при данном расчете.

Основная система при этом представляет собой ряд статически неопределимых балок, защемленных на одном конце и свободно опертых на другом или защемленных с двух концов.

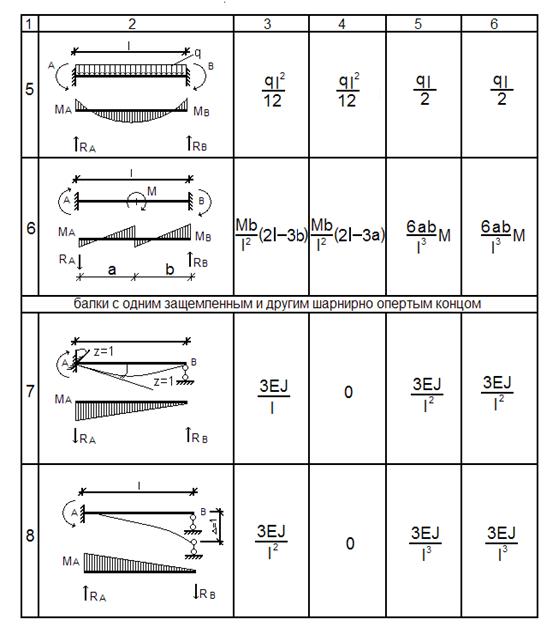
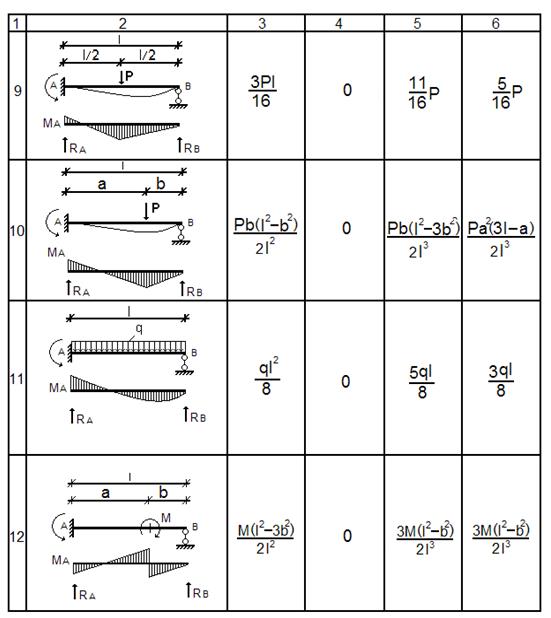
Эти балки заранее рассчитаны на все виды нагрузок (в табл. 5 приведены результаты таких расчетов, необходимые для расчета рамы на действие силовой нагрузки).

Таблица 5

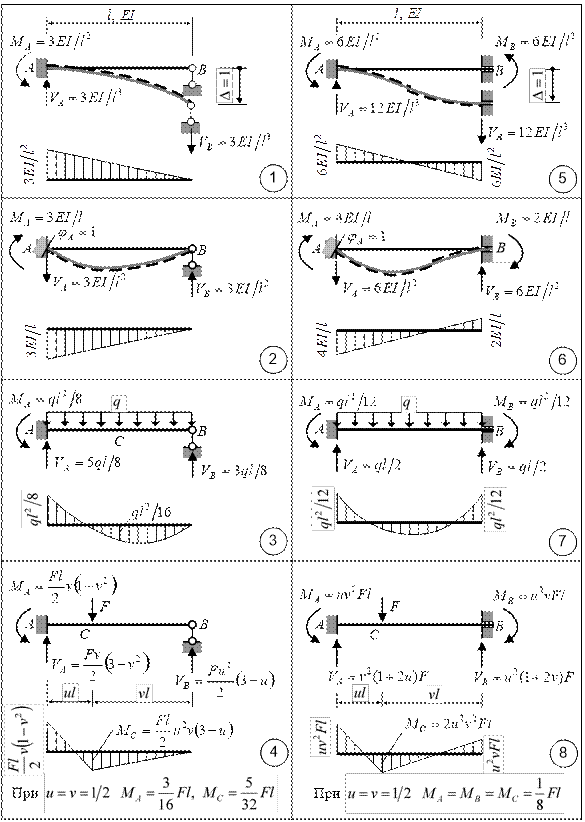
Поскольку в заданной раме узлы могут иметь перемещения, основную систему надо рассчитать на смещение этих узлов по направлению введенных связей.

Следующим этапом расчета является составление системы канонических уравнений. Физический смысл системы канонических уравнений метода перемещений состоит в том, что суммарная реакция в каждой дополнительной связи должна быть равна нулю. В общем виде система уравнений запишется так:

r₁₁∙z₁+ r₁₂∙z₂ + r₁₃∙z₃ + r₁₄∙z₄ +…+ r_1n∙z_n + R_1p = 0;

r₂₁∙z₁+ r₂₂∙z₂ + r₂₃∙z₃ + r₂₄∙z₄ +…+ r_2n∙z_n + R_2p = 0;

r₃₁∙z₁+ r₃₂∙z₂ + r₃₃∙z₃ + r₃₄∙z₄ +…+ r_3n∙z_n + R_3p = 0; (2)

………………………………………

r_n1∙z₁+ r_n2∙z₂ + r_n3∙z₃ +…+ r_nn∙z_n + R_np = 0.

где r_in – реактивная сила или реактивный момент во введенном стержне или в заделке i от смещения или поворота связи n на величину z_n = 1;

R_1p, R_2p, R_3p,… R_np – реактивное усилие или реактивный момент во введенном стержне или заделке n, вызванные действием данной нагрузки.

Для определения коэффициентов и свободных членов канонических уравнений необходимо построить эпюры изгибающих моментов от единичных перемещений и от заданной нагрузки в основной системе, т.е. эпюры от z₁ = 1; от z₂ = 1; от z₃ = 1 и т.д., а также М_р от заданной нагрузки.

Таких единичных эпюр будет столько, сколько дополнительных связей введено в систему. При их построении следует пользоваться таблицей 5.

Рекомендуется для каждого единичного смещения вычертить деформированную схему рамы с указанием растянутых волокон, что поможет правильно воспользоваться указанной таблицей.

Коэффициенты при неизвестных и свободные члены уравнений, представляющие реактивные усилия во введенных стержневых связях, могут быть определены из условий равновесия некоторой отсеченной части основной системы, содержащей эти связи. Реактивный момент считается положительным, если его направление совпадает с направлением поворота узла. Реактивное усилие считается положительным, если его направление совпадает с направлением линейного смещения закрепления. Определив коэффициенты при неизвестных и свободные члены канонических уравнений, необходимо выполнить их проверку. Проверка коэффициентов при неизвестных производится по следующей формуле:

где – сумма всех коэффициентов при неизвестных в канонических уравнениях;

Используя правило Верещагина, r_ss можно определить по выражению:

Проверка свободных членов уравнений производится следующим образом:

ΣR=R_sp, (5)

где ΣR=R_1p + R_2p + R_3p + R_np .

Применяя правило Верещагина, можно определить сумму всех свободных членов канонических уравнений по формуле

или

Здесь – суммарная эпюра изгибающих моментов от единичных перемещений, определяемая из уравнения:

– эпюра изгибающих моментов от действия нагрузки на статически определимую и геометрически неизменяемую систему, полученная от заданной статически неопределимой системы путем удалений лишних связей.

Изложенная выше проверка называется универсальной.

Если условия (4), (5) не выполняются, необходимо для отыскания ошибки провести построчные проверки:

где – сумма коэффициентов при неизвестных в первом уравнении;

По правилу Верещагина

аналогично

и т.д.

В развернутом виде это можно записать следующим образом:

r₁₁+ r₁₂ + r₁₃ + … + r_1n = r_1s ;

r₂₁ + r₂₂ + r₂₃ + … + r_2n = r_2s; (9)

..……………………………

r_n1 + r_n2 + r_n3 + … + r_nn = r_ns.

После определения и проверки коэффициентов при неизвестных и свободных членах канонических уравнений приступают к решению системы уравнений. Если уравнений больше двух, то рекомендуется решать их с помощью сокращенного алгоритма Гаусса. Сущность его сводится к последовательному исключению неизвестных. Если, например, имеем систему уравнений с n неизвестными, то в результате преобразования получаем сначала одно уравнение с n – 1 неизвестным, затем с n – 2 неизвестным, с n – 3 неизвестным и т.д. – до тех пор, пока не получим одно уравнение с одним неизвестным, которое будет легко решаться.

Найденное значение первого неизвестного подставляется во второе уравнение, содержащее два неизвестных. Определив их, подставляют значение в уравнение – и так до последнего уравнения, пока не будут определены значения всех неизвестных в системе. Решение производится в табличной форме (табл. 6). Разберем принцип решения на примере системы из трех уравнений.

Таблица 6

Номер уравнения	Неизвестные			Переходный коэффициент	Свободные члены
	z1	z2	z3	α	Rip
I	r11	r12	r13	α12=-r12/r11 α13=-r13/r11	R1p
2	r21	r22	r23		R2p
I∙α12	r11∙α12	r12∙α12	r13∙α12		R2p∙α12
Уравнение II=I∙α12+ 2
II	r12+r11∙α12=0	r22+r12∙α12=	r23+r13∙α12=	α23=-	R2p+R1p∙α12=

Получили уравнение II:

3	r31	r32	r33	R3p
I∙α13	r11∙α13	r12∙α13	r13∙α13	R1p∙α13
II∙α23	0	∙α13	∙α23	∙α23

Уравнение III получим, если суммируем уравнения 3+(I∙α₁₃)+(II∙α₂₃)

r13∙α13+∙α23+r33=

R1p∙α13+∙α23+R3p=

Получили уравнение III:

В результате преобразований получаем одно уравнение (III) с одним неизвестным, из которого определим z₃. Определив z₃ и подставив его значение в уравнение (II), найдем значение z₂. Подставляя в уравнение (1) значения z₂ и z₃, определяем значение z₁.

После решения системы канонических уравнений и определения неизвестных строят эпюры изгибающих моментов от найденных значений неизвестных (исправленные эпюры), т.е.

Сложив исправленные эпюры с эпюрой от нагрузки (M_p), получим окончательную эпюру изгибающих моментов в заданной системе от заданной нагрузки:

Производится статическая и кинематическая проверки полученной окончательной эпюры изгибающих моментов.

Первая заключается в проверке равновесия всех узлов эпюры М. Она имеет большое значение, так как у всех слагаемых эпюр узлы не уравновешены. Невыполнение условий равновесия узлов указывает на неправильность построения окончательной эпюры изгибающих моментов.

Кинематическая проверка состоит в выполнении следующего условия:

т.е. проинтегрировав окончательную эпюру M с единичной , построенной в статически определимой системе по направлению отброшенной связи; если в заданной системе эта связь была неподвижная, мы должны получить ноль. Можно также воспользоваться правилом Верещагина и перемножить указанные эпюры, после этого должен получиться ноль:

По полученной окончательной эпюре изгибающих моментов М, как и при расчете рам, методом сил строится эпюра поперечных сил Q, а по ней – эпюра нормальных сил N.

Статическая проверка эпюры моментов

Статическая проверка заключается в проверке равновесия узлов рамы.

Построение расчетной эпюры поперечных сил

Эпюра поперечных сил на каждом участке строится по уже проверенной расчетной эпюре моментов так же, как и в методе сил.

Построение расчетной эпюры продольных сил

Эпюра продольных сил строится, как и в методе сил по расчетной эпюре поперечных сил методом вырезания узлов.

Статическая проверка рамы в целом

В заданной системе отбрасываются опоры, их действие на раму заменяется усилиями согласно построенным эпюрам M, Q, N; проверяется выполнение уравнений равновесия рамы в целом.

Примеры расчет рамы методом перемещений

Пример 1.

Для заданной рамы (рис. 5) требуется:

а) раскрыть кинематическую неопределимость рамы;

б) построить эпюры M, Q и N;

в) произвести проверку правильности построения эпюр.

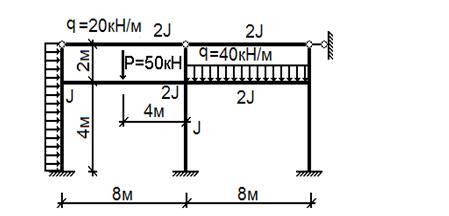
Рис.5. Заданная система

Решение:

I. Определяется число неизвестных перемещений:

а) число угловых перемещений n_y равно числу жестких узлов рамы n_y =3;

б) для определения количества независимых линейных смещений узлов рамы следует построить шарнирную схему рамы (рис.6) и воспользоваться формулой:

n_л=2y-C_ш; n_л=9∙2-17=1.

Итак, имеем 3 угловых перемещения и 1 линейное. Их можно представить схемой, изображенной на рис. 7.

II. Выбирается основная система путем введения дополнительных жестких и линейных связей (рис.8). В результате получим систему, состоящую из пяти балок, защемленных двумя концами, и трех балок, защемленных одним концом и с шарнирным опиранием другого конца.

III. Записывается система канонических уравнений:

r₁₁∙z₁+ r₁₂∙z₂ + r₁₃∙z₃ + r₁₄∙z₄ + R_1p = 0;

r₂₁∙z₁+ r₂₂∙z₂ + r₂₃∙z₃ + r₂₄∙z₄ + R_2p = 0;

r₃₁∙z₁+ r₃₂∙z₂ + r₃₃∙z₃ + r₃₄∙z₄ + R_3p = 0;

r₄₁∙z₁+ r₄₂∙z₂ + r₄₃∙z₃ + r₄₄∙z₄ + R_4p = 0.

IV. Для определения коэффициентов и свободных членов канонических уравнений для основной системы строятся единичные и грузовая эпюры моментов (рис.9).

V. Определяются коэффициенты и свободные члены канонических уравнений, т.е. реакции, возникающие в дополнительных связях в основной системе (табл.7).

VI. Выполняется проверка правильности определения коэффициентов и свободных членов уравнения. Для этого строится суммарная эпюра (рис.9):

Используя формулу =, производим проверку правильности определения коэффициентов при неизвестных:

Σr =3,5+4,5+1,6875+2∙(0,5+0,375+0,5+0,375+0,375)=17.437;

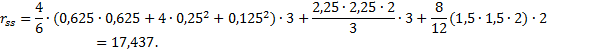
Используя формулу производим проверку правильности определения свободных членов:

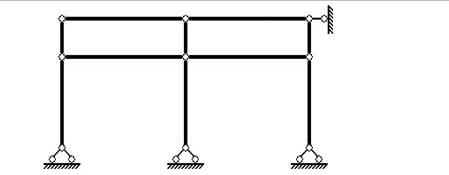
Рис.6. Шарнирная система

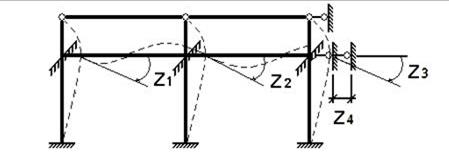
Рис.7. Деформированная система

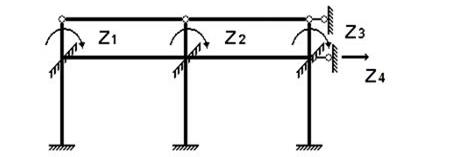
Рис.8. Основная система

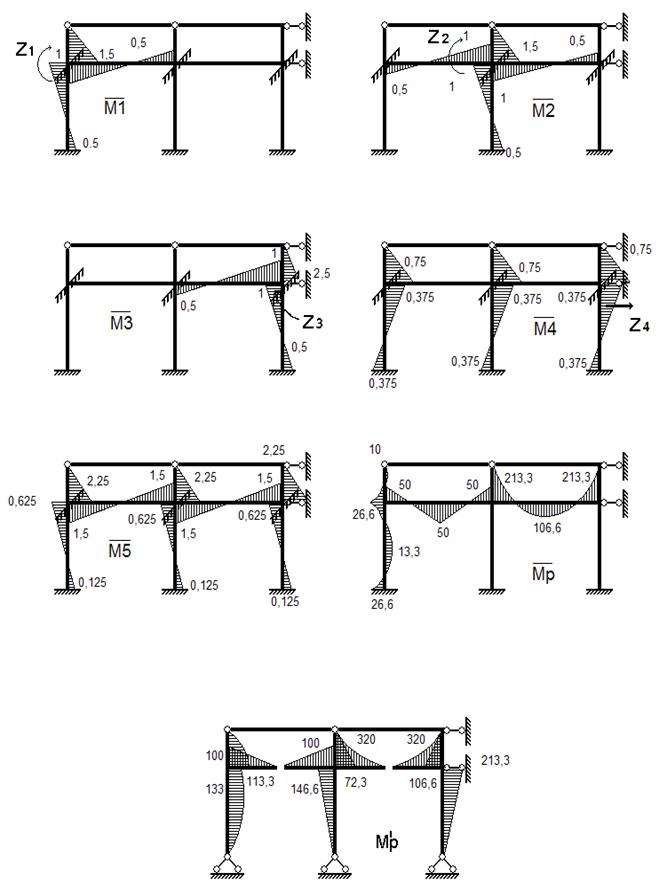
Рис.9. Исходные эпюры

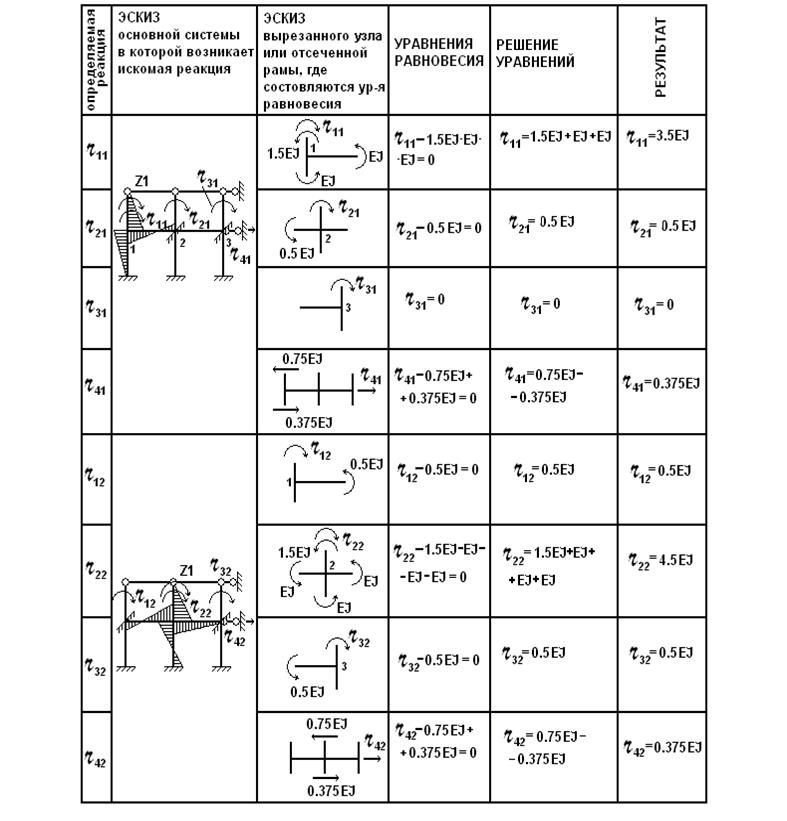
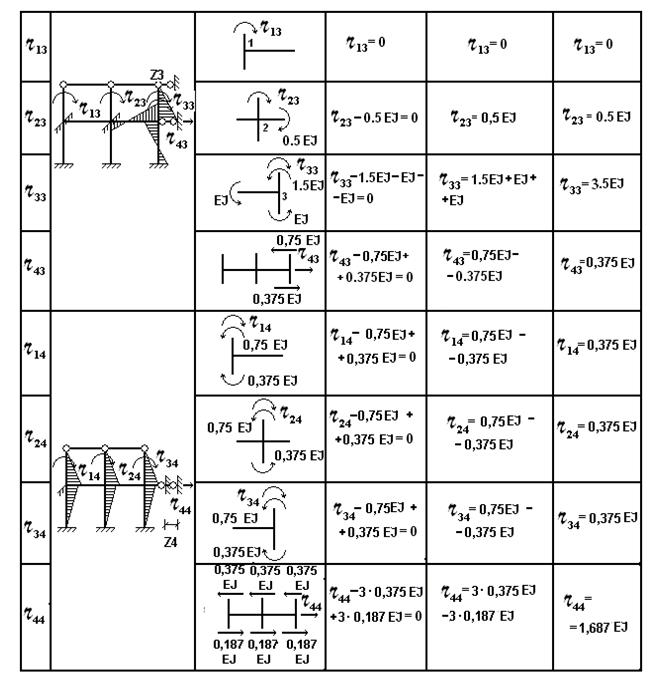
Таблица 7. Определение коэффициентов и свободных членов уравнений

ΣR=R_1p+R_2p+R_3p+R_4p.

=-33,333-163,333+213,333-65=-48,333.

VII. В систему канонических уравнений подставляются найденные цифровые значения коэффициентов и свободных членов уравнений:

3,5∙z₁+ 0,5∙z₂ + 0∙z₃ + 0,375∙z₄ -33,333 = 0;

0,5∙z₁+ 4,5∙z₂ + 0,5∙z₃ + 0,375∙z₄ -163,333 = 0;

0∙z₁+ 0,5∙z₂ + 3,5∙z₃ + 0,375∙z₄ -213,333 = 0;

0,375∙z₁+ 0,375∙z₂ + 0,375∙z₃ + 1,687∙z₄ -65 = 0.

VIII. Решается система канонических уравнений. Получены следующие значения неизвестных:

z₁= - 1,167; z₂= 40,579;

z₃= - 71,643; z₄=45,681.

Для проверки правильности решения полученные значения неизвестных подставляются во все канонические уравнения:

3,5∙(-1,167)+0,5∙40,579+0∙(-71,643)+0,375∙45,681-33,333=0,

откуда 0 = 0;

0,5∙(-1,167)+4,5∙40,579+(-71,643)∙0,5+0,375∙45,681-163,333=0,

откуда 0 = 0;

0∙(-1,167)+0,5∙40,579+3,5∙(-71,643)+0,375∙45,681-213,333=0,

откуда 0 = 0;

0,375∙(-1,167)+0,375∙40,579+0,375∙(-71,643)+1,687∙45,681-65=0,

откуда 0 = 0.

Построим эпюры (рис.10).

IX. Строится окончательная эпюра изгибающих моментов (рис.10):

Ординаты эпюр откладываются в сторону растянутых волокон.

X. Выполняется проверка правильности построения эпюры изгибающих моментов.

1. Статическая проверка.

Для ее осуществления достаточно проверить равновесие каждого узла (рис.11): ΣM=0.

2. Кинематическая проверка может быть выполнена или по замкнутому контору, или перемножением эпюр.

а) По замкнутому контуру: суммарная площадь эпюры М, деленная на I в любом замкнутом контуре, должна равняться нулю:

б) Перемножением эпюр: выбирается система для расчета рамы методом сил и строятся любые единичные эпюры от сил по направлению отброшенных связей (рис.12). Для любой выбранной системы необходимо получить, например,

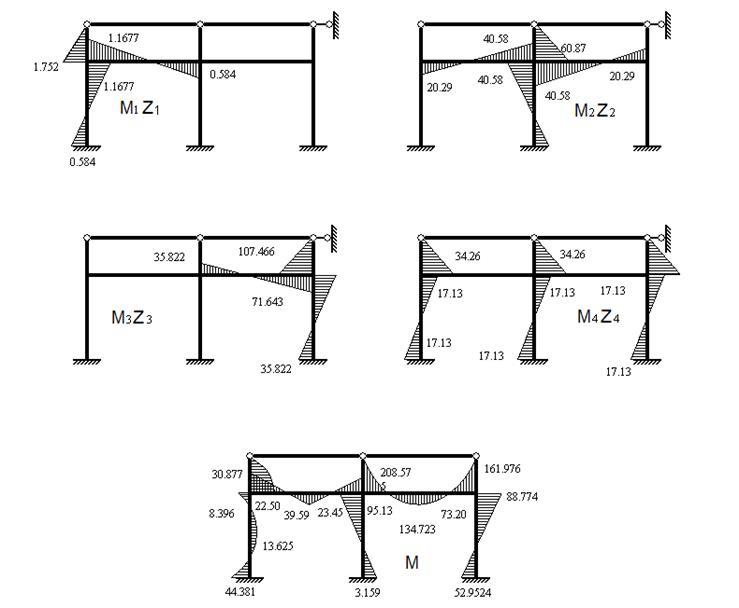
Рис.10. Исправленные и окончательные эпюры

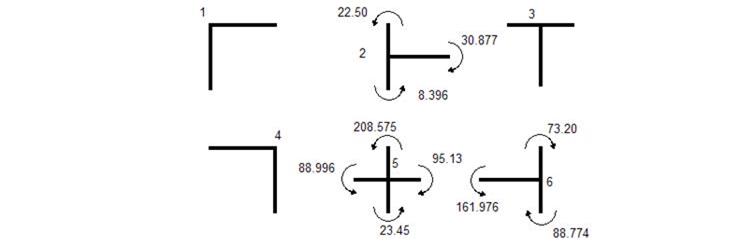
Рис.11. Проверка равновесия узлов

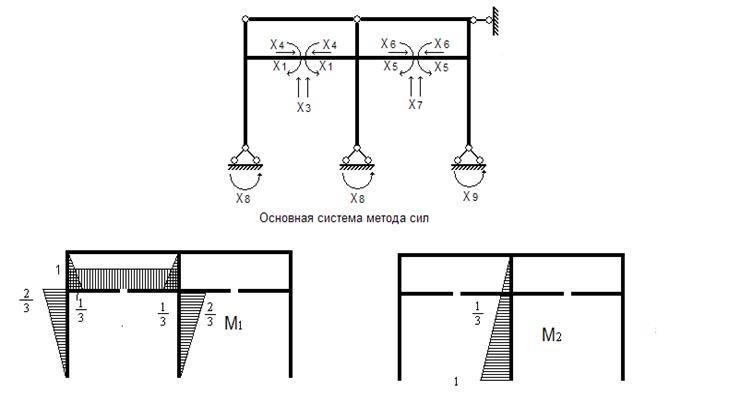
Рис.12. Единичные эпюры

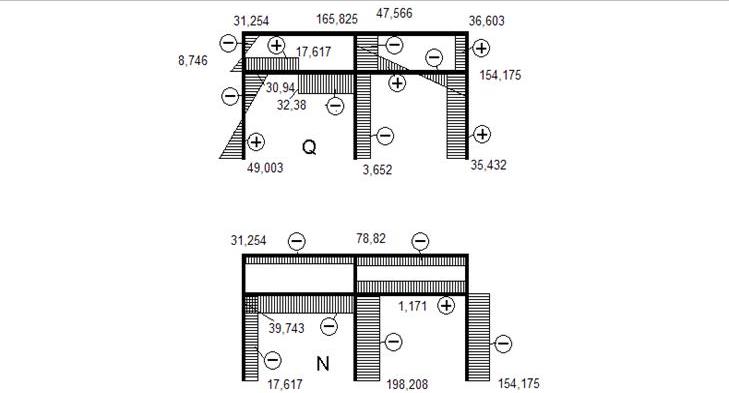
Рис.13. Эпюры поперечных и продольных сил

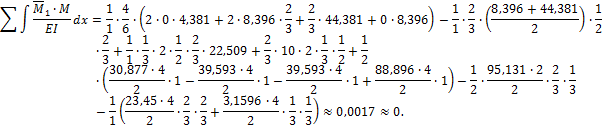
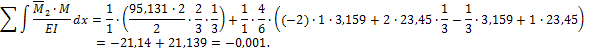
Погрешность: (0,001/21,13)∙100%=0,05%.

XI. По полученной эпюре изгибающих моментов строятся сначала эпюра поперечных сил, а затем эпюра продольных сил (рис.13).

XII. Выполняется статическая проверка вычислений, для этого рассматривается равновесие системы в целом (рис.14).

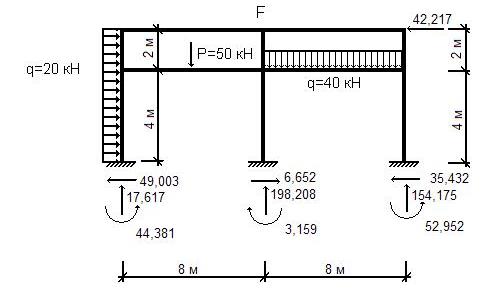
Рис.14. Равновесие системы в целом

Σx=0; 20∙6-49,003+6,652-35,432-42,217=0.

Σy=0; -50-40∙8+17,617+198,208+154,175=0.

ΣM_F=0; -20∙6∙3-50∙4+40∙8∙4+49,003∙6+17,617∙8-6,652∙6+35,432∙6-154,175∙8+3,159-52,952-44,381=-1930,652+1930,705≈0,053.

Погрешность: (0,053/1930,652)∙100%=0,003%.

Таблица 8. Приложение

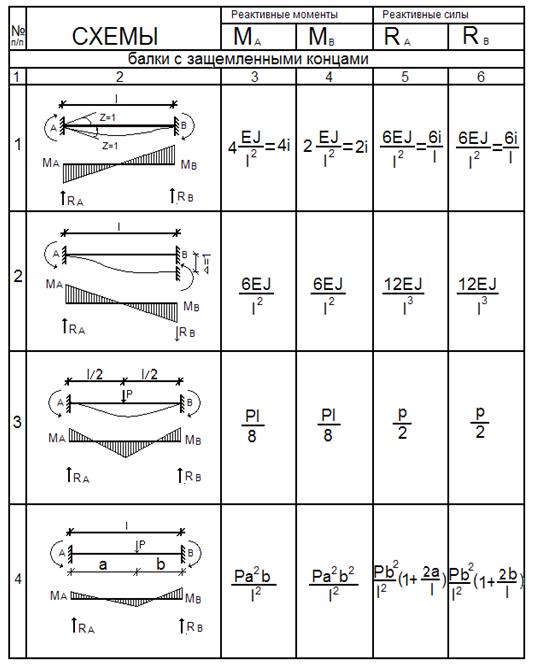
Пример 2.

Для рамы, изображенной на рис. 15, а, требуется построить эпюру изгибающих моментов и сравнить с результатами расчета методом сил.

1. Кинематический анализ, определение степени кинематической неопределимости n

Число угловых перемещений n_y=1 – один жесткий узел В. Для определения числа линейных перемещений во все жесткие узлы системы (узлы B, D, E) врезаем шарниры (рис. 16, а) и подсчитываем число степеней свободы получившейся системы:

n₀=3D-2Ш-C₀=3∙4-2∙3-5=1,

где D=4 – диски AB, BC, BD, CE; Ш=3 – шарниры В (двукратный) и С; С₀=5, поскольку имеются по две связи в шарнирах D, E и одна связь в шарнирно подвижной опоре A. Таким образом, имеем механизм с одной степенью свободы. На рис. 16, б показана схема малых перемещений этого механизма без деформации его элементов. Число линейных перемещений n_л=n₀=1. Степень кинематической неопределимости n=n_у+n_л=1+1=2.

Рис. 15. Расчет рамы методом перемещений

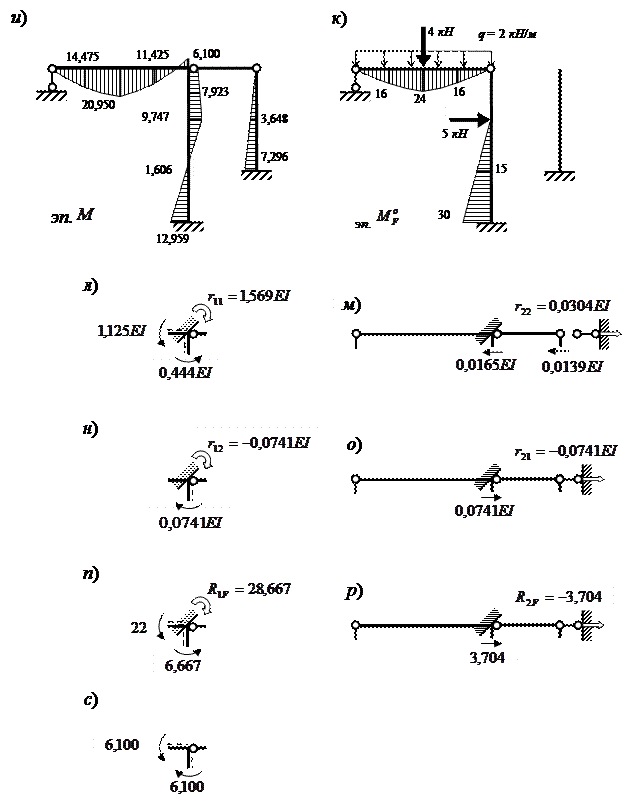
Рис. 15. Окончание

2. Выбор основной системы

Основная система получается из заданной введением защемляющей связи в узле В и линейной связи в узле С (рис. 15, б). В качестве неизвестных принимаются угол поворота z₁ жесткого узла и линейное перемещение z₂ горизонтальных элементов рамы.

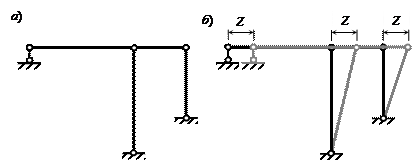
Рис. 16. К определению числа линейных перемещений

3. Формирование системы канонических уравнений метода перемещений

Для нашей задачи система канонических уравнений имеет вид

Здесь:

– реактивный момент в защемляющей связи, вызванный поворотом этой связи на единицу (реакция в связи 1 от );

– реактивный момент в защемляющей связи от действительного значения поворота z₁;

– реактивный момент в защемляющей связи, вызванный единичным линейным смещением (реакция в связи 1 от );

– реактивный момент в защемляющей связи от действительного значения линейного смещения z₂;

– реактивный момент в защемляющей связи от заданной нагрузки;

– реакция в линейной связи от поворота защемляющей связи (реакция в связи 2 от );

– реакция в линейной связи от действительного значения поворота z₁;

– реакция в линейной связи, вызванная единичным линейным смещением (реакция в связи 2 от );

– реакция в линейной связи от действительного значения линейного смещения z₂;

– реакция в линейной связи от заданной нагрузки.

Смысл первого уравнения состоит в требовании равенства нулю реакции в защемляющей связи 1, смысл второго уравнения – в требовании равенства нулю реакции в линейной связи 2. Именно при этих условиях основная система (рис. 15, б) будет работать эквивалентно заданной (рис. 15, а).

3.1. Построение единичных эпюр моментов

Единичные эпюры моментов и строятся в основной системе от и соответственно (рис. 15, в, г) с использованием табл. 9. Рекомендуется изобразить деформированную схему рамы и отметить на ней растянутые волокна (показаны пунктиром на рис. 15, в, г).

Таблица 9

Покажем подробнее построение эпюры от (рис. 15, в). В основной системе (рис. 15, б) стержень АВ представляет собой балку, шарнирно опертую с одной стороны и жестко заделанную с другой стороны. Кинематическим воздействием является единичный поворот жесткой заделки.

В табл. 9 этому случаю соответствует схема 2 (номер схемы в табл. 1 заключен в кружок). Для построения эпюры моментов на участке АВ следует схему 2 таблицы расположить на раме так, чтобы совпали растянутые волокна на схеме из таблицы и на деформированной схеме рамы.

Этого можно добиться зеркальным отражением схемы 2 относительно оси 1 – 1 и зеркальным отражением получившейся схемы относительно оси 2 – 2 (рис. 17, а). Значение момента в защемляющей связи подсчитывается с учетом заданной жесткости рассматриваемого элемента рамы: 3EI₁/l_AB=3∙3EI/8=1,125EI. Стержень BD в основной системе представляет собой балку, защемленную с обеих сторон. Кинематическим воздействием является единичный поворот заделки В. В табл. 9 этому случаю соответствует схема 6.

Совпадение растянутых волокон на схеме 6 и на деформированной схеме рамы достигается поворотом схемы 6 на 90⁰ по часовой стрелке (рис. 17, б). Эпюра строится аналогичным образом. Кинематическое воздействие приводит к единичному смещению: жесткой заделки для балки BD (схема 5 табл. 9); шарнирной опоры – для балки СЕ (схема 1 табл. 9). В обоих случаях табличные схемы следует повернуть на 90⁰ против часовой стрелки.

При этом

Суммарная единичная эпюра от перемещений и , действующих одновременно, строится суммированием единичных эпюр () и показана на рис. 15, д.

На рис. 15, в, г, д ординаты эпюр в начале участков выделены более крупным шрифтом в сравнение с ординатами в середине участков.

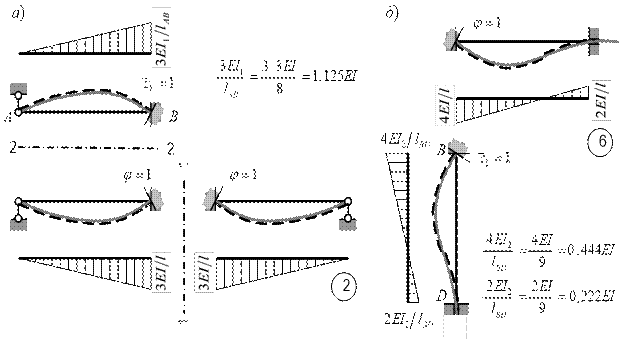
Рис.17. Построение единичных эпюр моментов

3.2. Определение коэффициентов системы канонических уравнений

Коэффициент r₁₁ – реакцию в связи 1 от – определяем из условия равновесия узла В (рис. 15, л). Для этого рассматриваем эп.  (единичную эпюру от ) и проводим процедуру метода сечений: 1) вырезаем узел В; 2) отбрасываем оставшуюся часть рамы; 3) действие отброшенной части заменяем силами взаимодействия (на рис. 1, л показаны только моменты, необходимые в дальнейшем при составлении уравнения равновесия); 4) из условия равновесия ΣM=0: r₁₁-1,125EI-0,444EI=0 определяем r₁₁=1,125EI+0,444EI=1,569EI.

Остановимся подробнее на п. 3 метода сечений. Согласно эп. для стержня AB в точке В, момент равен 1,125EI и растягивает верхние волокна (ординаты эп. отложены сверху, см. также деформированную схему на рис. 1, в). Для стержня BD в точке В момент равен 0,444EI и растягивает левые волокна (ординаты эп. отложены слева, см. также деформированную схему на рис. 15, в).

На рис. 1, л растянутые волокна в стержнях узла В отмечены пунктиром; моменты 1,125EI и 0,444EI направлены так, чтобы растягивать отмеченные пунктиром волокна.

Реакцию в связи 1 от линейного смещения определяем аналогично из условия равновесия узла В (рис. 15, н), рассматривая эп. : r₁₂= -0,0741EI.

Реакцию в связи 2 от поворота определяем из условия равновесия фрагмента рамы, показанного на рис. 15, о, рассматривая эп. . Из сил взаимодействия с отброшенной частью рамы показаны только горизонтальные силы (поперечные силы для балок из таблицы), необходимые в дальнейшем для составления уравнения равновесия ΣF_x=6EI/9²+r₂₁=0, где x – горизонтальная ось. Из указанного уравнения равновесия находим

r₂₁=6EI/9²=-0,0741EI.

Аналогично, рассматривая эп. , находим реакцию r₂₂ (рис. 15, м): r₂₂=12EI/9³+3EI/6³=0,0165EI+0,0139EI=0,0304EI

3.3. Проверка коэффициентов канонических уравнений

Поскольку , то можно переходить к следующему пункту алгоритма.

3.4. Построение грузовой эпюры изгибающих моментов

Грузовая эпюра моментов M_F строится в основной системе от заданной нагрузки с использованием табл. 9 (рис. 15, е). В нашем случае для балки АВ эта процедура показана на рис. 18 (схема 4 при u=v=0,5 плюс схема 3).

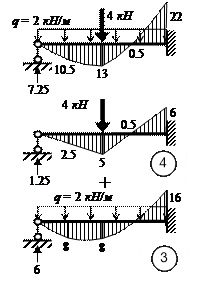
Рис. 18. Построение грузовой эпюры

В случае действия на балку нескольких нагрузок грузовая эпюра получается суммированием эпюр от каждой нагрузки в отдельности. Для балки DB согласно табл. 9 (схема 8) имеем:

u=2/3; v=1/3;

момент под силой равен

Реакция

3.5. Определение свободных членов канонических уравнений

Коэффициент R_1F – реакцию в связи 1 от заданной нагрузки (рассматриваем, следовательно, эп. M_F) – определяем из условия равновесия узла В (рис. 15, п): R_1F=22+6,667=28,667.

R_2F – реакцию в связи 2 от заданной нагрузки – определяем из условия равновесия ΣF_x=3,704+R_2F=0 фрагмента рамы, изображенного на рис. 15, р: R_2F= -3,704.

3.6. Проверка свободных членов канонических уравнений

Построим эп.  – эпюру моментов от заданной нагрузки в любой основной системе метода сил. Можно в качестве эп.  принять эп. M_F метода сил (рис. 9.15, е, см. раздел «Расчет рам методом сил»). Рекомендуется, однако, выбрать такую основную систему метода сил, чтобы эп.  была как можно проще – см. рис. 15, к. Тогда

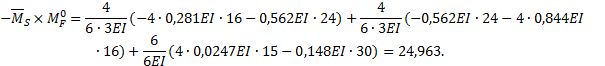
Поскольку

то переходим к следующему пункту алгоритма.

4. Решение системы канонических уравнений

Система канонических уравнений с учетом подсчитанных значений коэффициентов приобретает вид:

Решая эту систему уравнений каким-либо способом (например, так, как это показано в п. 4 алгоритма метода сил) получаем:

z₁= -14,134/EI; z₂=87,538/EI.

5. Построение расчетных эпюр изгибающих моментов, поперечных и продольных сил

5.1. Построение расчетной эпюры моментов

Строим исправленные эпюры ∙z₁, ∙z₂ (рис. 15, ж, з). Расчетная эпюра моментов (рис. 15, и) получается сложением грузовой эпюры (рис. 15, е) с единичными исправленными: M=M_F+∙z₁+∙z₂. Данная процедура подробно описана в алгоритме метода сил.

5.2. Статическая проверка эпюры моментов

Проверяем равновесие жесткого узла В (рис. 15, с). Узел уравновешен: ΣM=6,100-6,100=0.

Последующие пп. 5.3 – 5.5 алгоритма метода перемещений выполняются так же, как и в методе сил.

Пример 3.

Для статически неопределимой рамы (рис. 19) с заданными размерами и нагрузкой требуется построить эпюры изгибающих моментов, поперечных и продольных сил.

Примечание. На ригеле осевой момент инерции I₁, на стойке I₂.

Обозначим . Тогда

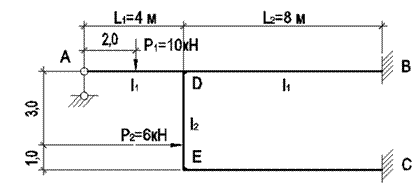
Рис. 19. Заданная рама

Решение:

Находим степень кинематической неопределимости рамы:

n=n_y+n_л,

Здесь n_y=2 (рамные узлы D и E).

Число независимых линейных смещений узлов n_л находим как степень свободы шарнирно-стержневой системы, полученной введением шарниров во все узлы рамы.

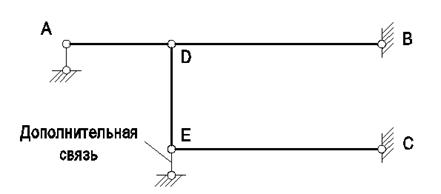
Рис. 20

n_л=2У-С-С₀=2∙5-4-5=1.

Для геометрической неизменяемости системы необходима дополнительная опорная связь в узле Е (или в узле D) (рис.20).

Отметим, что узлы D и E могут смещаться только по вертикали.

Таким образом,

n=2+1=3.

Образуем основную систему (рис.21), введя связи, препятствующие возможным перемещениям узлов. Выбираем направления неизвестных перемещений и записываем систему канонических уравнений:

r₁₁∙Z₁+ r₁₂∙Z₂ + r₁₃∙Z₃ + R_1p = 0;

r₂₁∙Z₁+ r₂₂∙Z₂ + r₂₃∙Z₃ + R_2p = 0;

r₃₁∙Z₁+ r₃₂∙Z₂ + r₃₃∙Z₃ + R_3p = 0.

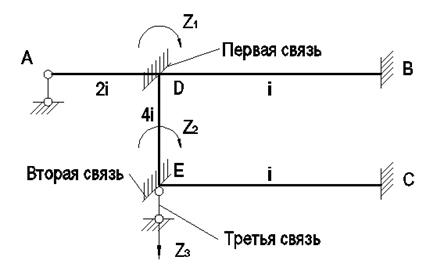
Рис. 21. Основная система

Вычислим погонные жёсткости на каждом участке рамы:

Примем за , тогда

Найденные значения покажем на участках рамы.

Построим эпюры моментов от единичных перемещений введённых связей и от нагрузки, используя таблицы реакций (рис.22)

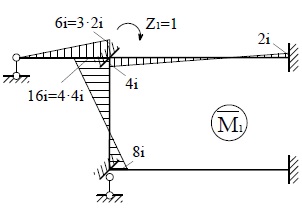
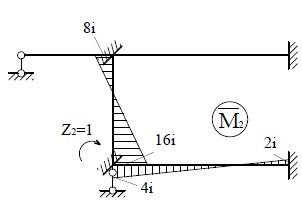
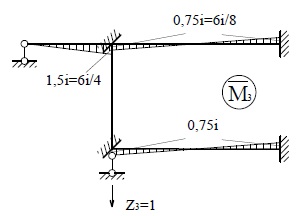
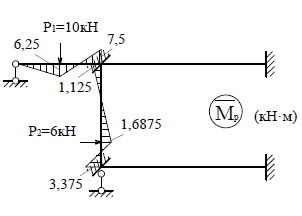
Рис.22

Реактивные моменты в первой и второй связях определяются вырезанием узлов D и E с введёнными связями, а реактивное усилие в третьей связи способом разреза элементов рамы и рассмотрения уравнений равновесия отсечённой части.

Неизвестную реакцию (момент или силу) будем считать положительной, если её направление совпадает с принятым направлением поворота или линейного смещения узла.

Вырезаем узлы D и E на эпюрах и из уравнений равновесия узла вида ΣM=0 находим коэффициенты и свободные члены первых двух канонических уравнений.

Покажем, например, определение и .

Узел D (рис.23,а) (эпюра )

Узел Е (рис.23,б) (эпюра ) .

следовательно,

а)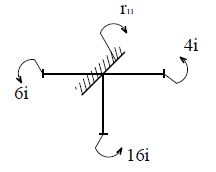 б)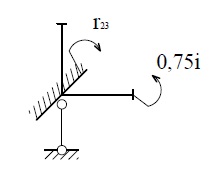

Рис.23

Аналогично определяются и другие реактивные моменты в связях 1 и 2. Выпишем результаты вычислений:

По теореме о взаимности реакций имеем:

Усилия и в 3-й связи находим с помощью сечения I - I, которое при разрезании участков рамы выявляет поперечные силы, лежащие на одной оси с определяемой реакцией.

Эпюра , сечение I – I (рис.24).

Уравнение равновесия отсечённой части рамы:

следовательно,

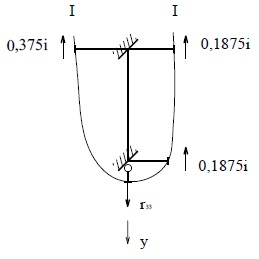
Рис.24

Эпюра M_p (рис.25)

откуда кН.

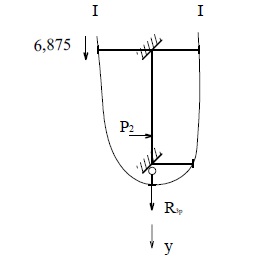
Рис.25

Система уравнений примет вид:

Решение этой системы даёт:

Для получения окончательной эпюры М воспользуемся соотношением:

На заданной раме наметим расчётные сечения (рис.26).

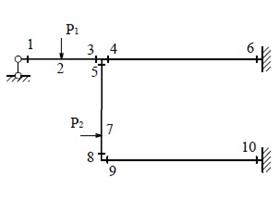
Рис.26

Построим эпюры моментов M₁, M₂ и M₃ от найденных значений неизвестных («исправленные эпюры») (рис.27). Сложив эти эпюры с эпюрой M_{р ,} получим окончательную эпюру моментов (рис.28). Результаты расчёта представим в табл.10.

Таблица 10

Номер сечения	M1	M2	M3	Mр	M
1	0	0	0	0	0
2	0,0224	0	7,0	6,25	13,27
3	0,0449	0	14,0	-7,5	6,55
4	-0,0299	0	7,0	0	6,97
5	0,12	1,424	0	-1,125	0,42
6	0,015	0	-7,0	0	-6,98
7	-0,015	-1,78	0	1,6875	-0,108
8	-0,06	-2,848	0	-3,375	-6,28
9	0	-0,712	7,0	0	6,28
10	0	0,356	-7,0	0	-6,64

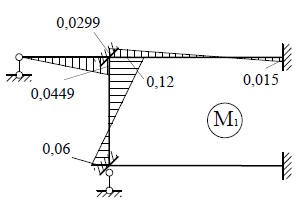
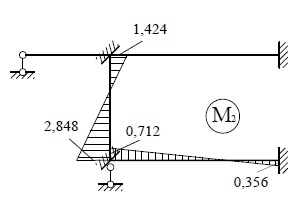
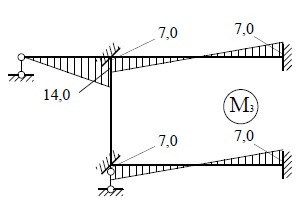
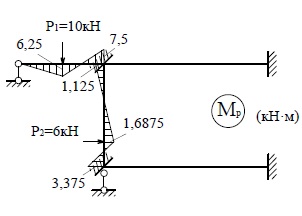
Рис.27

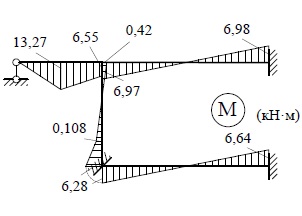
Рис.28

Статическая проверка эпюры М на рис.29.

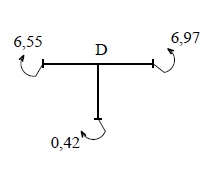
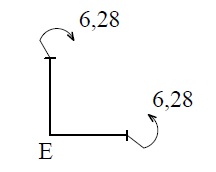
Рис.29

Дополнительно сделаем кинематическую проверку подобно тому, как это делается в методе сил (рис.30).

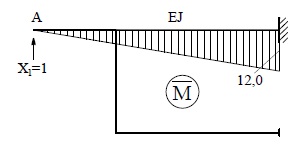
Рис.30. Основная система метода сил

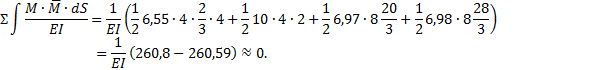
Следовательно, расчёт верный.

Эпюры Q и N строим так же, как в методе сил (рис.31).

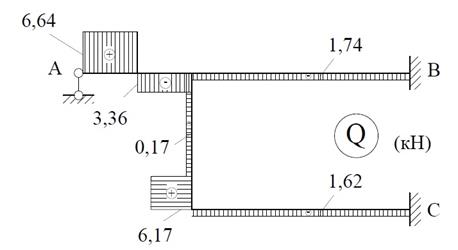
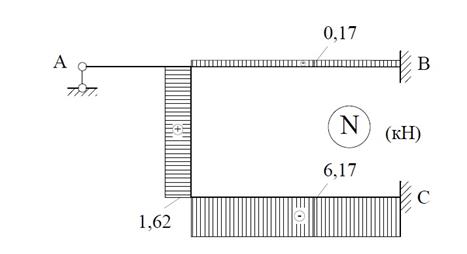
Рис.31

Проверкой эпюр Q и N служит проверка равновесия сил для всей рамы (рис.32).

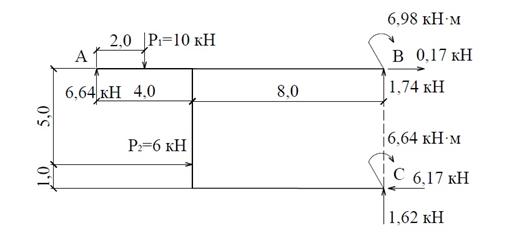
Рис.32

ΣY=6,64 – 10 + 1,74 + 1,62 = 10 - 10=0

ΣX=6 + 0,17 - 6,17 = 6,17 - 6,17=0

ΣM_B=-6,64∙12 + 10∙10 +6∙3 – 6,17∙4 – 6,98 – 6,64 = 118 - 117,98 ≈0.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00