29. Расчет статически неопределимых систем методом
перемещений на температурные и кинематические воздействия
29.1. Стандартные задачи метода перемещений при расчете на
температурное воздействие
Для расчета сооружений методом перемещений на температурные воздействия необходимо иметь эпюры внутренних усилий для отдельных стержней, составляющих набор стандартных задач, от изменения температуры со стороны их краевых волокон.
Будем считать постоянными вдоль оси любого к-го стержня
величины жесткостей EJk, EAk поперечного
сечения, высоты поперечного сечения hk, коэффициента
линейного температурного расширения материала 
и
приращения температуры 
.
Считая эпюру приращений температур по высоте поперечного сечения линейной, представим ее в виде суммы двух эпюр, одна из которых характеризует неравномерные приращения температур (рис. 29.1,б), а другая – равномерные (рис. 29.1,в).
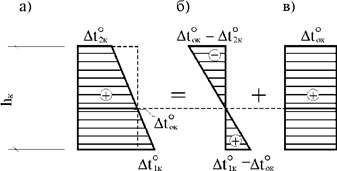
Рис. 29.1
Напоминаем, что характеристикой
неравномерного приращения температуры является величина 
– перепад приращений температуры по высоте поперечного
сечения, а равномерного 
–
приращение температуры на уровне центра тяжести поперечного сечения. Величина определяется по эпюре приращений температуры при известном положении центра тяжести
поперечного сечения. В частности, для поперечных сечений с двумя осями
симметрии
Рассмотрим решение одной из стандартных задач
методом сил на температурное воздействие, в частности, построение, эпюры
изгибающих моментов для стержня, показанного на рис. 29.2,а. Для любого сечения стержня примем 
Основная система метода сил показана на рис. 29.2,б. Усилие в лишней связи X1 получим из уравнения
Используя эпюру изгибающих моментов М1
от X1=1
(рис. 29.2,в) и условную эпюру
изменения величины 
по
длине стержня, ординаты которой откладываются со стороны более «теплых» волокон
(рис. 29.2,г), получим:
так как в основной системе метода сил от X1=0 N1=0.
Из уравнения (1) найдем неизвестное метода сил
где 
Окончательную эпюру М построим, используя соотношение
М = М1X1 (рис. 29.2,д).
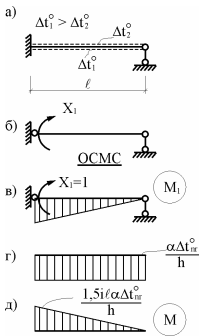
Рис.29.2
Результат решения аналогичной задачи для стержня, защемленного с двух концов, приведен на рис. 29.3,а. Ординаты полученных эпюр изгибающих моментов (рис.29.2,д и 29.3,а) от изменения температуры откладываются со стороны более «холодных» волокон.
На рис. 29.3,б приведена эпюра продольных сил для стержня, ограниченного по
концам цилиндрическими шарнирами, от равномерного нагрева всех волокон на 
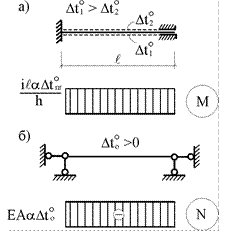
Рис.29.3
29.2. Расчет стержневых статически
неопределимых систем на температурное воздействие
В плоской n раз кинематически неопределимой стержневой системе краевые
волокна всех или части элементов испытывают воздействие температурного поля
(рис. 29.4,а). Характеристиками
этого поля для k-го стержня сооружения
являются: перепад приращения температуры по высоте поперечного сечения 
и
приращение температуры на уровне его центра тяжести
(см. п. 29.1).
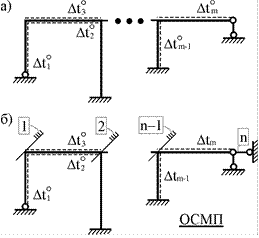
Рис.29.4
Наложением n угловых и линейных связей образуем основную систему метода перемещений заданного сооружения (рис. 29.4,б). Неизвестные угловые и линейные перемещения его узлов Z1, Z2,…, Zi,…, Zj,…, Zn определим из условий равенства нулю реакций в наложенных связях от их смещения на величины Z1, Z2,…, Zi,…, Zj,…, Zn и от заданного изменения температуры.
Используя принцип независимости действия, получим систему канонических уравнений метода перемещений для определения неизвестных Z1, Z2,…, Zi,…, Zj,…, Zn в случае температурного воздействия на сооружение
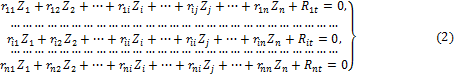
Величины главных rii и побочных rij коэффициентов системы уравнений (8.29) не зависят от вида воздействия на сооружение.
Свободные члены системы канонических уравнений (2) Rit – это реакции в i-х наложенных связях от изменения температуры в основной системе метода перемещений. Они определяются по эпюрам внутренних усилий (в рамках и балках – по эпюрам изгибающих моментов), построенным в основной системе от температурного воздействия статическим способом, т.е. из условий равновесия узлов и отдельных частей сооружения.
Эпюра изгибающих моментов 
от
изменения температуры в основной системе метода перемещений складывается из
двух эпюр: – от
неравномерных приращений температуры и эпюры
– от равномерных.
Для построения эпюры изгибающих моментов от
неравномерных приращений температуры используются стандартные задачи, приведенные в
п. 29.1 настоящей главы (см. рис. 29.2,д
и 29.3,а).
Равномерное приращение температуры в
основной системе метода перемещений вызывает линейные смещения узлов сооружения
и, следовательно, перекосы его элементов, численные значения которых можно
получить, используя план перемещений. В данном случае при построении этого
плана необходимо учитывать продольные перемещения стержней, вызванные их
равномерным нагреванием или охлаждением. Зная перекосы стержней, эпюру
изгибающих моментов в
основной системе метода перемещений построим с помощью стандартных задач,
полученных от линейных кинематических воздействий.
Окончательную эпюру изгибающих моментов Mt в заданном сооружении от температурного воздействия после решения системы уравнений (2) получим, используя соотношение:
В формуле (3)
.
Эпюры поперечных и продольных сил Qt и Nt построим по эпюре изгибающих моментов Mt , используя условия равновесия отдельных элементов и узлов заданного сооружения.
Эпюры внутренних усилий Mt, Qt и Nt, полученные методом перемещений, построены правильно, если выполнена статическая проверка решения задачи, т.е. если все узлы и любые части заданного сооружения находятся в равновесии.
29.3. Расчет стержневых статически
неопределимых систем на смещение опорных связей
В плоской n раз кинематически
неопределимой стержневой системе (рис. 29.5,а) m угловых и
линейных опорных связей получили смещения, численные значения которых
соответственно равны 
По-прежнему изгибные жесткости поперечных
сечений элементов сооружений будем считать постоянными.
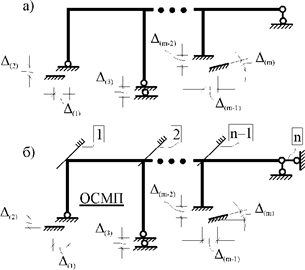
Рис. 29.5
Наложением n угловых и линейных связей на узлы сооружения образуем основную систему метода перемещений (рис. 29.5,б). Неизвестные перемещения узлов Z1, Z2,…, Zi,…, Zj,…, Zn определим, отрицая в основной системе реакции в наложенных связях от их смещения на величины Z1, Z2,…, Zi,…, Zj,…, Zn и от заданного кинематического возмущения опорных связей, т.е. из системы канонических уравнений
Свободные члены Ric системы
уравнений (4) – это реакции в i-х
наложенных связях в основной системе метода перемещений от заданного смещения
опорных связей. В рамах и балках они определяются статическим способом по эпюре
изгибающих моментов 
, построенной в основной системе метода
перемещений от заданных кинематических воздействий. Для построения эпюры
изгибающих моментов используются стандартные задачи.
После решения системы уравнений (4) окончательную эпюру изгибающих моментов Мс в заданном сооружении от смещения опорных связей получим, используя принцип независимости действия сил:
Решение задачи завершается построением эпюр поперечных и продольных сил Qc и Nc по известной эпюре изгибающих моментов Мс и статической проверкой правильности расчета.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Теория машин и механизмов
