Главная
30. Учет симметрии статически неопределимых сооружений при
их расчете методом перемещений
30.1. Общие положения
В этой главе рассматриваются стержневые системы, геометрия и распределение жесткостей поперечных сечений элементов которых обладают хотя бы одной осью симметрии.
Как и в методе сил для расчета симметричных
сооружений будем использовать симметричную основную систему метода перемещений,
а также группировку неизвестных угловых и линейных перемещений симметрично
расположенных узлов.
Если в основной системе метода перемещений все эпюры внутренних усилий от единичных перемещений узлов (в том числе и групповых) имеют симметричный или обратно симметричный характер, то система канонических уравнений метода перемещений при произвольном внешнем воздействии (силовом, температурном или кинематическом) распадается на две независимых друг от друга системы уравнений, одна из которых содержит только симметричные неизвестные, а другая – только обратно симметричные (по аналогии с методом сил).
Если во всех единичных состояниях симметричной основной системы метода перемещений эпюры внутренних усилий симметричны или обратно симметричны, то в случае симметричных внешних воздействий обратно симметричные неизвестные метода перемещений будут равны нулю, а в случае обратно симметричных воздействий равны нулю симметричные неизвестные.
30.2. Группировка угловых перемещений
узлов
Рассмотрим расчет рамы с вертикальной осью
симметрии на произвольную нагрузку (рис. 30.1,а). Соотношение между погонными жесткостями симметрично
расположенных ригелей 1А, 2В 
и
стоек 1С, 2D ic, а также
центрального ригеля 12 
, задано. Степень кинематической
неопределимости рамы равна двум. На рис. 30.1,б показана основная система метода перемещений для этой рамы.
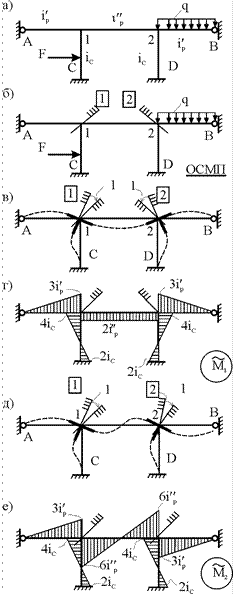
Рис.30.1
Неизвестные углы поворотов узлов 1 и 2 рассматриваемой рамы от заданной нагрузки Z1 и Z2 определяются из системы канонических уравнений
Нетрудно убедиться в том, что в нашем случае, принимая за неизвестные углы поворота отдельных узлов, мы будем иметь полную систему уравнений (1), т.е. ни один из коэффициентов при неизвестных Z1 и Z2 не будет равен нулю (предлагаем читателям самостоятельно проверить это).
Используем симметрию рамы и произведем группировку угловых перемещений симметрично расположенных узлов 1 и 2. Каждое из уравнений системы (1) отрицает в основной системе метода перемещений реакции R1 и R2 в наложенных угловых связях 1 и 2 от их поворота на углы, равные Z1 и Z2, и от заданной нагрузки, т.е. первое уравнение удовлетворяет условию R1 = 0, а второе – R2 = 0. Эти условия будут выполнены, если в основной системе метода перемещений будем одновременно отрицать разность и сумму реакций в наложенных связях 1 и 2, т.е. если будем отрицать групповые реакции
Групповым реакциям 
и 
соответствуют групповые угловые перемещения
узлов 1 и 2 
, которые в дальнейшем будем называть
групповыми неизвестными метода перемещений.
В единичном состоянии
основной системы метода перемещений неизвестному групповому перемещению 
соответствует одновременный поворот угловой
связи, наложенной на узел 1, по часовой стрелке на угол, величина которого
равна единице, и угловой связи, наложенной на узел 2, – против часовой стрелки
на такой же угол – другими словами, симметричная деформационная схема элементов
рамы и симметричная групповая эпюра изгибающих моментов 
(рис. 30.1,в,г). Аналогично,
групповому неизвестному перемещению 
в
основной системе метода перемещений соответствует обратно симметричная схема
деформаций и обратно симметричная групповая эпюра изгибающих моментов 
(рис. 30.1,д,е).
При построении групповых эпюр изгибающих
моментов и для
всех элементов рамы, кроме центрального ригеля 12, использованы стандартные
задачи метода перемещений. На ригеле 12 эпюры изгибающих моментов можно
получить суммированием соответствующих эпюр от симметричного поворота двух
угловых связей на угол 
(рис. 30.2,а) и от обратно симметричного поворота этих же связей на такой же
угол (рис. 30.2,б).
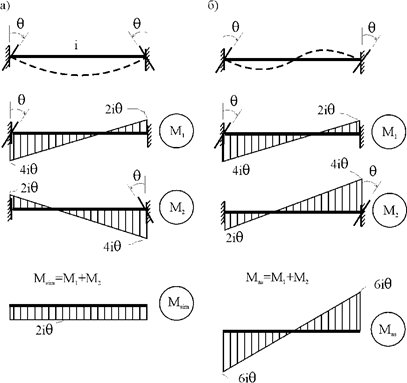
Рис. 30.2
Система канонических уравнений (1) для групповых неизвестных метода перемещений перепишется:
Коэффициенты при неизвестных 
и свободные члены 
системы уравнений (2) можно вычислить
сопряжением соответствующих эпюр изгибающих моментов, либо из условия
равновесия одновременно двух узлов, содержащих симметрично расположенные связи.
Так как групповые эпюры и носят
соответственно симметричный и обратно симметричный характер, то
С учетом последнего обстоятельства система уравнений (2) распадается на два независимых друг от друга уравнения:
При построении эпюр внутренних усилий в заданном сооружении групповые неизвестные метода перемещений используются как обычные. В частности, для рамы, показанной на рис. 30.1,а имеем:
где MF – эпюра изгибающих моментов в основной системе метода перемещений от заданной нагрузки.
30.3. Группировка линейных перемещений
узлов
Группировка линейных перемещений симметрично расположенных узлов целесообразна, если при выборе основной системы метода перемещений наложение линейных связей на узлы производится без нарушения симметрии сооружения.
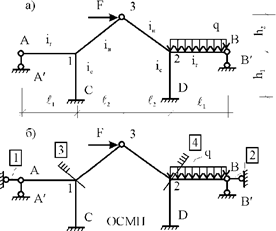
Рис. 30.3
Поясним это на примере рамы, имеющей
вертикальную ось симметрии (рис. 30.3,а).
Степень кинематической неопределимости этой рамы равна четырем (
=2, 
=2). Для ее расчета предлагается
симметричная основная система метода перемещений, показанная на рис. 30.3,б. Рассмотрим группировку линейных
перемещений узлов А и В рамы, приняв за неизвестные
групповые линейные перемещения, а именно: сумму и
разность 
линейных перемещений этих узлов Z1 и Z2, т.е.
В единичном состоянии основной системы
метода перемещений неизвестному групповому перемещению соответствует одновременное смещение линейных
связей 1 и 2, наложенных на узлы А и В, направо на
величину, равную единице, другими словами, обратно симметричная деформационная
схема элементов рамы и обратно симметричная групповая эпюра изгибающих моментов
(рис. 30.4).
Неизвестному групповому перемещению в
основной системе метода перемещений соответствует одновременное единичное
смещение связей 1 и 2 в разные стороны, т.е. симметричная деформационная схема
и симметричная групповая эпюра изгибающих моментов 
(рис. 30.5).
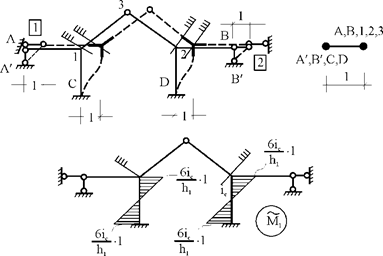
Рис. 30.4
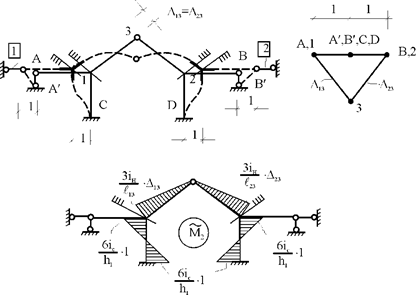
Рис. 30.5
Учитывая обратно симметричный характер
групповой эпюры изгибающих моментов 
и
симметричный – 
, получим
Следствием группировки линейных и угловых перемещений симметрично расположенных узлов сооружения является упрощение системы канонических уравнений метода перемещений за счет исключения из нее нулевых побочных коэффициентов.
30.4. Расчет статически неопределимых систем методом
перемещений в матричной форме
30.4.1. Теорема о работе концевых
усилий и ее приложение к плоским стержневым системам
В основе расчета статически неопределимых систем методом перемещений в матричной форме лежит теорема о работе концевых усилий. Поясним сначала содержание и доказательство этой теоремы в общем виде.
Пусть требуется определить реакцию Rik в i-й связи заданного сооружения (рис. 30.6,а), испытывающего в k-м равновесном состоянии любые внешние воздействия (силовые, температурные, кинематические).
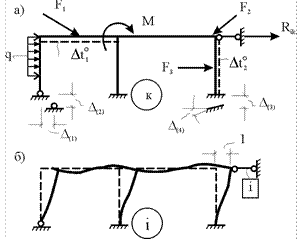
Рис.30.6
Рассмотрим вспомогательное i-е состояние сооружения, в котором i-я связь получила единичное перемещение (рис. 30.6,б) и введем следующие обозначения:
g – число узлов сооружения;
m – число его стержней (элементов);
Wext,j – возможная работа внешних сил, приложенных к j-му элементу в k-м состоянии сооружения, на перемещениях этого элемента, вызванных единичным смещением i-й связи;
Wint,j – возможная работа внутренних сил j-го элемента в k-м состоянии сооружения на тех же перемещениях (напоминаем читателям о том, что эта работа отрицательна);
Wext,h – возможная работа внешних сил, приложенных к узлу h в k-м состоянии сооружения, на тех же перемещениях.
Используем принцип Лагранжа для k-го равновесного состояния всего сооружения (рис. 30.6,а), приняв за возможные перемещения, имеющие место в i-м состоянии (рис. 30.6,б)
Рассмотрим отдельный j-й элемент сооружения (рис. 30.7,а). В его концевых сечениях действуют силы, которые в дальнейшем будем называть концевыми усилиями. Обозначим через Aj возможную работу концевых усилий j-го элемента k-го равновесного состояния сооружения на перемещениях концов этого элемента в i-м состоянии (рис. 30.7,б). Запишем условие равновесия отдельного j-го элемента в форме Лагранжа, приняв, по-прежнему, за возможные – перемещения в i-м состоянии сооружения
Из зависимости (4) для отдельного элемента следует, что
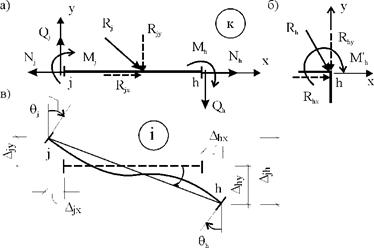
Рис. 30.7
Для полного ансамбля разобщенных друг от друга элементов сооружения, используя (5), имеем:
Подставив выражение (6) в соотношение (3), окончательно получим математическую формулировку теоремы о работе концевых усилий:
В общей форме теорема о работе концевых усилий может быть прочитана так: реакция i-й связи k-го равновесного состояния сооружения равна работе концевых усилий его элементов и взятой с обратным знаком работе узловых сил на перемещениях, вызванных единичным смещением i-й связи.
Конкретизируем
эту теорему для плоских стержневых систем.
Концевое сечение отдельного элемента,
примыкающее к узлу h, обозначим через h (рис. 30.7,а), а противоположное концевое сечение –
через j (в
соответствии с номером рассматриваемого элемента). Нагрузку, действующую на j-й элемент, заменим
равнодействующей Rj. Проекции этой
равнодействующей на оси y и
x обозначим соответственно
через Rjy и Rjx (рис. 30.7,а).
На узел h (рис. 30.7,б) действуют сосредоточенный момент 
и
произвольная сосредоточенная сила Rh (ее проекции на оси y и x – Rhy и Rhx).
В концевых сечениях элемента j действуют концевые усилия: концевые изгибающие моменты Mj и Mh, концевые поперечные силы Qj и Qh и концевые продольные силы Nj и Nh. На рис. 30.7,а показаны положительные концевые усилия. Особо следует подчеркнуть, что концевой изгибающий момент считается положительным, если он элемент вращает по часовой стрелке, и отрицательным, – если против часовой стрелки.
Из условий равновесия j-го элемента получим:
На рис. 30.7,в показаны угловые и линейные перемещения концевых сечений j-го элемента в i-м состоянии. Повороты концевых сечений элементов будем считать положительными, если они происходят по часовой стрелке, и отрицательными, – если против часовой стрелки. Взаимное смещение концов j и h в направлении, перпендикулярном оси стержня до его деформации (в направлении оси y), называется перекосом j-го элемента. Из рис. 30.7,в видно, что
Перекос j-го элемента считается положительным, если в результате линейных перемещений концов j и h его поворот совершается по часовой стрелке, и отрицательным, – если против часовой стрелки.
Так как в расчетах стержневых систем методом перемещений пренебрегают изменениями длин их элементов под воздействием продольных сил, то взаимное смещение концов j и h j-го элемента в направлении его оси (в направлении оси x) равно нулю, т.е.
Вернемся к соотношению (7) и вычислим его правую часть для плоских стержневых систем.
Для отдельного j-го элемента имеем:
С учетом соотношений (8)–(10) возможная работа концевых усилий j-го элемента на перемещениях, имеющих место в i-м состоянии (рис. 30.7,б) перепишется:
Для всех элементов заданного сооружения работа концевых усилий суммируется
причем
составляющие Rjy и Rjx
равнодействующей нагрузки, приложенной к j-му элементу, работу
совершают на линейных перемещениях узла h (
и
), происходящих в i-м
состоянии (рис. 30.7,в). Как
видно из рис. 30.7,а, узел h расположен
в стороне, противоположной концевому сечению
j, т.е. сечению, в
котором зафиксирована концевая поперечная сила Qj.
Работа узловых сил, действующих на отдельный узел h (рис. 30.7,б), на перемещениях этого узла, совпадающих с перемещениями концевого сечения h j-го элемента в i-м состоянии, будет равна:
Для всех узлов стержневой системы выражение (14) суммируется от h до g
Подставив соотношения (13) и (15) в формулу (7), окончательно получим математическую формулировку теоремы о работе концевых усилий для плоских стержневых систем:
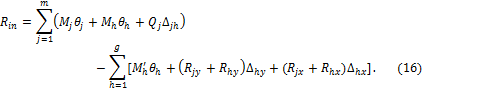
В матричной форме выражение (16) перепишется:
Поясним смысл матриц, входящих в соотношение (17):
Rk – матрица искомых реакций в связях стержневой системы, находящейся в k-м равновесном состоянии при любых заданных внешних воздействиях (силовых, температурных, кинематических);
Sk – матрица концевых усилий элементов сооружения (изгибающих моментов Mj и Mh и поперечных сил Qj), возникающих в k-м состоянии от заданных внешних воздействий;
– матрица нагрузок (сосредоточенных моментов
и сосредоточенных
сил (Rjy + Rhy), (Rjx + Rhx), действующих
на узлы сооружения в k-м равновесном
состоянии;
a –
матрица концевых перемещений элементов стержневой системы (углов поворота
концевых сечений 
и 
отдельных стержней и их перекосов
) от единичного смещения связей, в которых
определяются реакции от заданных внешних воздействий;
с – матрица угловых θh и линейных перемещений и узлов
от единичного смещения связей, где определяются реакции в k-м равновесном состоянии
сооружения.
Число столбцов в матрицах Rk, Sk и равно
числу вариантов внешних воздействий, а в матрицах a и с – числу
связей, в которых определяются реакции от заданных воздействий. Число строк в
матрице Rk соответствует числу связей, где необходимо определить
реакции в k-м равновесном состоянии
сооружения.
30.4.2. Определение реакций в наложенных
связях в основной системе метода перемещений
от различных воздействий в матричной
форме
В дальнейшем за k-е равновесное состояния сооружения будем принимать его основную систему метода перемещений. Рассмотрим сначала определение в матричной форме реакций в наложенных связях основной системы метода перемещений от внешних воздействий (силовых, температурных, кинематических). Используем для решения этой задачи матричное соотношение (8.52), опуская в нем индекс «k»
Элементы матриц R, 
, 
, a, c, входящих в выражение (18),
имеют прежний смысл (см. п. 30.4.1), но теперь они определяются для основной
системы метода перемещений. Конкретизируем содержание элементов перечисленных
матриц для нашего случая.
R – матрица реакций в наложенных связях основной системы метода перемещений от внешних воздействий
Здесь RF, Rt, Rc – реакции в наложенных связях соответственно от силовых, температурных и кинематических воздействий. Число столбцов матричных блоков RF, Rt, Rc определяется числом комбинаций указанных типов воздействий.
– матрица концевых усилий элементов
сооружения в основной системе метода перемещений от внешних силовых,
температурных и кинематических воздействий
– матрица узловых нагрузок в основной
системе метода перемещений. В этой матрице отличными от нуля будут элементы
только блока F, описывающего силовое
воздействие на сооружение. Блоки, соответствующие температурным и
кинематическим воздействиям, будут нулевыми. В общем случае матрица имеет
вид:
Напоминаем читателям: равнодействующие Rjy и Rjx нагрузок, приложенные к отдельным элементам, передаются на
узлы h, т.е. узлы,
расположенные противоположно по отношению к тем сечениям j, где при формировании матрицы фиксировались концевые поперечные силы Qj. Число
столбцов в матричных блоках 
матриц и соответствует числу столбцов в блоках RF, Rt и Rc матрицы R.
a – матрица концевых перемещений стержней в основной системе метода перемещений, вызванных смещением наложенных угловых и линейных связей на величину, равную единице.
с – матрица углов поворота и линейных перемещений узлов в основной системе метода перемещений от смещения наложенных на узлы сооружения связей на величину, равную единице.
Число столбцов в матрицах a и с равно числу угловых и линейных связей, накладываемых на узлы сооружения при образовании его основной системы метода перемещений, т.е. равно степени кинематической неопределимости сооружения.
Далее рассмотрим определение в матричной форме реакций в наложенных угловых и линейных связях в основной системе метода перемещений от смещения этих связей на величину, равную единице. Если степень кинематической неопределимости сооружения равна n, то матрица реакций в наложенных связях запишется в общем виде:
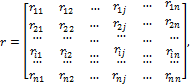
где rij – реакция в i-й наложенной связи от смещения j-й наложенной связи на величину, равную единице, в основной системе метода перемещений.
Для вычисления элементов матрицы r используем соотношение (8.53). Теперь в нем 
, так как в рассматриваемом равновесном
состоянии узловые силы отсутствуют. Введя другие обозначения (r вместо R и 
вместо ), получим:
В матричной зависимости (19)
– матрица
концевых усилий стержней сооружения в основной системе метода перемещений от
смещения наложенных на узлы связей на величину, равную единице. Эту матрицу
можно представить в виде произведения
где K – матрица концевых усилий стержней от единичных перемещений их концевых сечений в основной системе метода перемещений. Так как в основной системе метода перемещений мы имеем набор ограниченного количества стандартных стержней, элементы матрицы K для каждого стержня из этого набора могут быть получены заранее. Матрица K для всего сооружения запишется
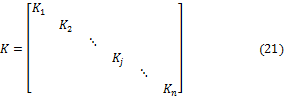
В матрице (21) блок Кj – это стандартная матрица внутренней жесткости j-го стержня.
После подстановки соотношения (20) в матричную зависимость (19) получим
Квазидиагональная матрица K называется матрицей внутренней жесткости сооружения.
30.4.3. Стандартные матрицы внутренней
жесткости элементов сооружений
Рассмотрим подробно формирование матрицы K, т.е. матрицы концевых
усилий, вызванных единичными перемещениями концевых сечений, для стержня,
защемленного с одного конца и шарнирно опертого – с другого (рис. 30.8,а). В соответствии с теоремой о работе
концевых усилий для любого стержня необходимо фиксировать оба концевых
изгибающих моментов и в одном из концов (по выбору) концевую поперечную силу.
Так как для рассматриваемого стержня изгибающий момент в сечении около
шарнирной опоры равен нулю, то можно ограничиться вычислением только двух
концевых усилий: концевого изгибающего момента и концевой поперечной силы в
сечении 1. Условимся вычисление этих концевых усилий производить сначала от
положительного поворота угловой связи заделки на величину, равную единице
(первое воздействие – рис. 30.8,б),
затем – от положительного единичного перекоса стержня (второе воздействие –
рис. 30.8,в). Для вычисления
концевых усилий от рассматриваемых воздействий используем стандартные задачи
метода перемещений, при =1 и 
=1 (рис. 30.8,б,в).
С учетом установленного порядка фиксации концевых усилий и единичных концевых перемещений стандартная матрица внутренней жесткости для рассматриваемого стержня запишется:
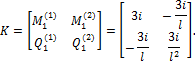
Если концевую поперечную силу, как и прежде, фиксировать во вторую очередь, но теперь уже в сечении 2 (рис. 30.8,г), то вид матрицы внутренней жесткостей для рассматриваемого стержня не изменится
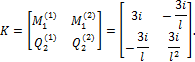
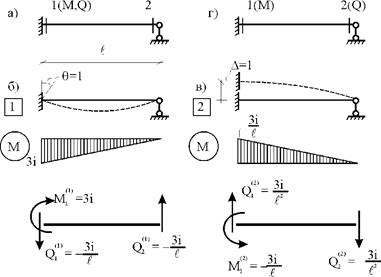
Рис. 30.8
Аналогично может быть получена матрица внутренней жесткости для стержня, защемленного с двух концов (рис. 30.9,а). С учетом установленного порядка записи концевых усилий (рис. 30.9,а) и нумерации единичных концевых перемещений (рис. 30.9,б,в,г) получим:
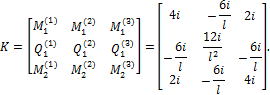
Самостоятельно можно убедиться в том, что вид матрицы K для защемленного с двух концов стержня не изменится, если, не меняя порядка записи ее строк и столбцов, поперечную силу будем брать в сечении 2, а не в сечении 1 (рис. 30.9,д).
Наконец, для шарнирно опертого с двух концов стержня концевая поперечная сила в любом из его сечений около шарнирной опоры от единичного перекоса будет равна нулю, т.е. для такого стержня матрица внутренней жесткости примет вид:
K = [0].
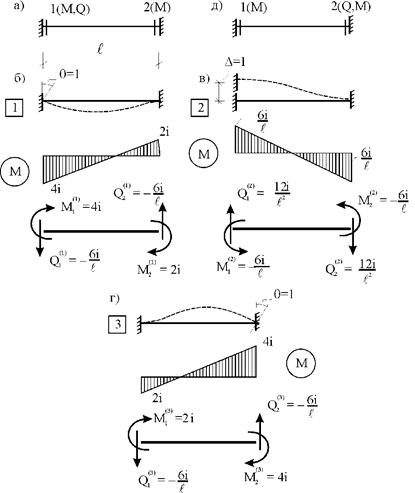
Рис. 30.9
30.4.4. Матричная форма расчета статически
неопределимых систем методом перемещений
Систему канонических уравнений метода перемещений представим в матричной форме:
rZ + R = 0. (23)
r – матрица коэффициентов при неизвестных системы канонических уравнений (23), или матрица реакций в наложенных связях от их смещения на величину, равную единице, в основной системе метода перемещений. Эта матрица называется матрицей внешней жесткости сооружения.
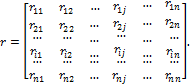
Число строк и столбцов матрицы внешней
жесткости сооружения равно степени его кинематической неопределимости nkin, т.е.
матрица r –
квадратная матрица. В силу теоремы о взаимности реакций матрица r симметрична. Так как система уравнений
(23) разрешима, то определитель матрицы r не равен нулю (det r
0). Это значит, что матрица внешней
жесткости является невырожденной матрицей.
Z – матрица неизвестных метода перемещений, или матрица угловых и линейных перемещений узлов сооружения от заданных внешних воздействий (силовых, температурных, кинематических).
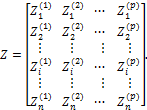
R – матрица свободных членов системы канонических уравнений метода перемещений (23), или матрица реакций в наложенных связях от заданных внешних воздействий в основной системе метода перемещений.
Число строк в матрицах Z и R равно степени кинематической неопределимости сооружения, а число столбцов – суммарному числу заданных независимых силовых, температурных и кинематических воздействий на сооружение.
Ранее на базе теоремы о работе концевых усилий были получены матричные соотношения (18) и (22) для вычисления элементов матриц r и R. Напомним их:
.
Смысл элементов матриц, включенных в формулы
(18) и (22) подробно изложен в п. 30.4.2 и 30.4.3.
Решая систему уравнений (23), получим матрицу неизвестных метода перемещений:
– матрица, обратная по отношению к матрице
внешней жесткости сооружения.
где E – единичная матрица.
После подстановки соотношений (18) и (22) в матричное выражение (24) получим:
Используем принцип независимости действия сил для определения концевых усилий в элементах заданного сооружения при силовых, температурных и кинематических воздействиях:
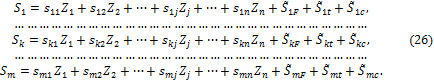
m – число концевых усилий (концевых изгибающих моментов и концевых поперечных сил), определяемых при решении конкретной задачи.
Группа
соотношений (26) в матричной форме перепишется:
S – матрица концевых усилий элементов заданного сооружения от внешних силовых, температурных и кинематических воздействий.
Напомним, что – это
матрица концевых усилий элементов сооружения в основной системе метода
перемещений от внешних силовых, температурных и кинематических воздействий, а
матрица –
матрица концевых усилий в основной системе метода перемещений от единичных
смещений наложенных связей (см. п. 30.4.2).
=
.
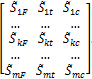
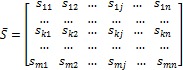Ранее было показано, что матрица выражается через матрицу внутренней жесткости
сооружения K и
матрицу перемещений концевых сечений стержней в основной системе от единичных
смещений наложенных связей a (см. п. 30.4.2)
следующим образом:
После подстановки матричных выражений (20) и (25) в матричную формулу (27) получим матричное соотношение для расчета стержневых систем методом перемещений
При силовом воздействии на сооружение, когда
S =
SF, 
, структура матричной зависимости (28)
сохраняется:
В случае температурного воздействия S = St, 
и,
следовательно,
При кинематическом воздействии, в частности, при смещении опорных связей, матричная зависимость для определения концевых усилий в стержнях заданного сооружения аналогична матричной зависимости (30):
Проверка правильности расчета заданного сооружения методом перемещений производится на основе теоремы о работе концевых усилий. Подставив значения концевых усилий S, вычисленных по формуле (29), в матричное выражение (17), мы должны получить нулевые значения реакций в несуществующих в заданном сооружении наложенных связях. Таким образом, в общем случае внешних воздействий имеем:
Матричное соотношение (32) при силовых воздействиях перепишется:
В случае температурных или кинематических
воздействий в матричной зависимости (32) следует принять S =
St или S = Sс,
. Проверочные матричные соотношения для этих
видов внешних воздействий примут вид:
или 
.
30.4.5. Пример расчета плоской рамы методом
перемещений на силовое воздействие в матричной форме
Для концевых сечений элементов статически неопределимой рамы (рис. 30.10) вычислить расчетные изгибающие моменты и соответствующие им поперечные и продольные силы. Постоянная нагрузка показана на рис. 30.10,а, временная – на рис. 30.10,б. Соотношение между изгибными жесткостями поперечных сечений стержней рамы известно:
EJab : EJeС : EJaе : EJAa = 2 : 2 : 1 : 1,25.
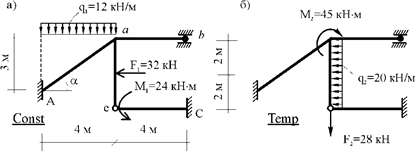
Рис. 30.10
Порядок расчета рамы в матричной форме на заданное силовое воздействие определяется соотношением (29):
1. Подготовительный этап расчета:
определение степени кинематической неопределимости рамы (
), выбор основной системы метода перемещений
(рис. 30.11,а), построение в
основной системе метода перемещений деформационных схем элементов рамы от
единичных смещений наложенных связей (рис. 30.11,б,в) и эпюр изгибающих моментов от
постоянной и временной нагрузок (рис. 30.11,г,д). Читателям предлагается все операции подготовительного этапа
выполнить самостоятельно, повторив, при необходимости, основные положения
девятнадцатой лекции.
2. Нумерация стержней рамы и их
концевых сечений (рис. 30.12). В скобках около номеров концевых сечений
указаны концевые усилия (изгибающие моменты и поперечные силы), которые в
дальнейшем будут вычисляться при формировании матрицы 
. Указанный порядок вычисления концевых
усилий позволяет использовать для расчета рамы стандартные матрицы внутренней
жесткости ее элементов, полученные в п. 30.4.3.
3. Вычисление погонных жесткостей стержней рамы. Сохраняя соотношение между изгибными жесткостями поперечных сечений элементов рамы, будем считать:
EJab = EJeС = 8, EJae = 4, EJAa = 5.
Относительные погонные жесткости стержней рамы в этом случае примут следующие значения:
4. Формирование матриц K и
a и
вычисление матрицы коэффициентов при неизвестных системы канонических уравнений метода
перемещений. Используем стандартные матрицы
внутренней жесткости элементов рамы, полученные в п. 30.4.3.
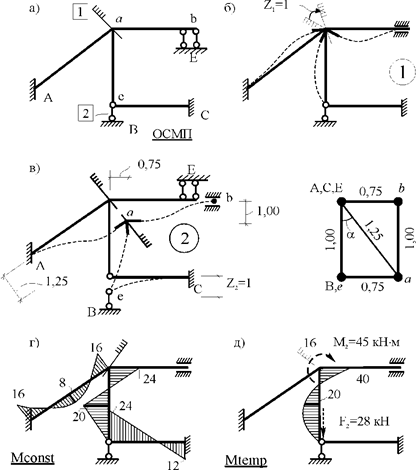
Рис. 30.11
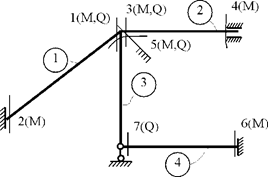
Рис.
30.12
Для первого (наклонного) стержня (рис. 30.12) при i = 1
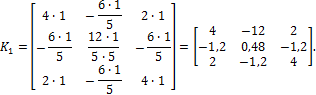
Для второго (верхнего горизонтального) стержня при i = 2
Для третьего (вертикального) стержня при i = 1
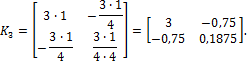
Для четвертого (нижнего горизонтального) стержня при i = 2
Матрица внутренней жесткости рамы в целом запишется:
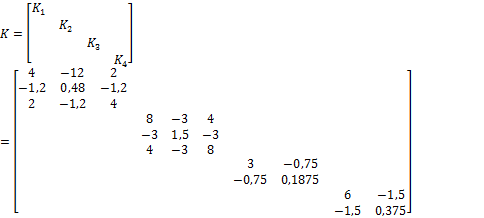
Для формирования матрицы а – матрицы концевых перемещений стержней от единичных смещений наложенных связей в основной системе метода перемещений, используем деформационные схемы, показанные на рис. 30.11,б,в.
В соответствии с принятой нумерацией стержней рамы и их концевых сечений (рис. 30.12) в первом столбце матрицы а фиксируем повороты концевых сечений и перекосы стержней от единичного смещения угловой связи по часовой стрелке (рис. 30.11,б), а во втором – эти же перемещения, но от единичного смещения линейной связи, наложенной на узел e, вниз (рис. 30.11,в). При этом полезно помнить, что в основной системе метода перемещений от смещения угловых связей отсутствуют перекосы стержней, а от смещения линейных связей – повороты концевых сечений стержней.
Напомним читателям правило знаков для концевых перемещений (см. п. 30.4.1): повороты концевых сечений считаются положительными, если они происходят по часовой стрелке, и отрицательными, – если против часовой стрелки; перекос стержня считается положительным, если его поворот совершается по часовой стрелке, и отрицательным, – если против.
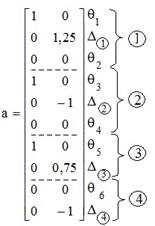
Транспонированная матрица имеет вид:
Имея матрицы ат, K, а, вычислим матрицу внешней жесткости сооружения, или матрицу коэффициентов при неизвестных системы канонических уравнений метода перемещений.
5. Обращение матрицы внешней жесткости сооружения.
6. Формирование матриц , F, с и вычисление матрицы свободных членов системы канонических уравнений метода
перемещений RF.
Элементы матрицы концевых усилий стержней
рамы получим, используя эпюры изгибающих моментов Mconst (рис. 30.11,г)
и Mtemp (рис. 30.11,д),
полученные в основной системе метода перемещений от заданных нагрузок. Концевые
изгибающие моменты и поперечные силы фиксируем в порядке, установленном
нумерацией концевых сечений стержней рамы и последовательностью их записи.
Правило знаков для концевых усилий было установлено в п. 30.4.1: концевой
изгибающий момент и концевая поперечная сила считаются положительными, если они
вращают стержень по часовой стрелке, и отрицательными, – если против часовой
стрелки. Для вычисления концевых поперечных сил используются уравнения
равновесия для отдельных стержней. В первом столбце матрицы записываются концевые усилия от постоянной
нагрузки, во втором – от временной нагрузки.
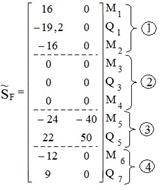
Формированию
матрицы узловых нагрузок F предшествует перенос равнодействующих нагрузок, приложенных к отдельным
стержням, на узлы, расположенные противоположно концевым сечениям, в которых
при формировании матрицы фиксировались концевые поперечные силы
(рис. 30.13). Обход узлов производится в строго установленном порядке,
например, узлы А, а, b, e, C
(рис. 30.13). С целью сокращения числа строк
в матрице F можно не принимать во внимание узлы, к которым во
всех сочетаниях нагрузок не приложены сосредоточенные силы и сосредоточенные
моменты, т.е. можно не фиксировать нулевые значения этих узловых воздействий. В
нашем примере – это узлы b и С (рис. 30.13). В дополнение к этому в матрицу F не следует включать сосредоточенные силы,
действующие на узлы, не имеющие в заданном сооружении линейных перемещений, так
как работа этих сил на перемещениях таких узлов равна нулю (см. формулировку
теоремы о работе концевых усилий в п. 30.4.1 настоящей лекции). В
рассматриваемом примере – это узел А (рис. 30.13),
на который действует вертикальная сосредоточенная сила 
кН. Таким образом, при формировании матрицы F в нашем
случае можно ограничиться описанием узловых нагрузок, действующих на узлы a и e (рис. 30.13).
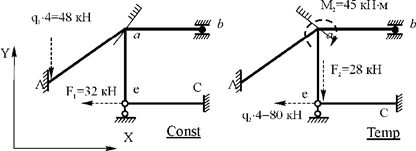
Рис.
30.13
Знаки сосредоточенных узловых сил, включаемых в матрицу F, привязываются к принятой системе координат (оси x и y на рис. 30.13). Сосредоточенные узловые моменты считаются положительными, если они вращают узлы по часовой стрелке, и отрицательными, – если против часовой стрелки.
Условимся для каждого узла сначала записывать горизонтальную сосредоточенную силу, затем – вертикальную сосредоточенную силу, и в последнюю очередь – узловой сосредоточенный момент. При отсутствии во всех сочетаниях внешних силовых воздействий какой-либо из перечисленных компонент ее нулевые значения в матрицу F для рассматриваемого узла можно не включать. Первый столбец матрицы F описывает постоянную узловую нагрузку, второй – временную узловую нагрузку.
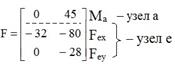
Элементы матрицы c должны описывать перемещения узлов в основной системе метода перемещений в направлении узловых сосредоточенных сил и сосредоточенных моментов, включенных в матрицу F, от единичных смещений наложенных связей. Для формирования матрицы c используем деформационные схемы рамы в основной системе метода перемещений, полученные от смещения наложенных связей на величину, равную единице (рис. 30.11,б,в). Первый столбец этой матрицы включает в себя угол поворота узла а, горизонтальное и вертикальное перемещение узла e от единичного поворота угловой связи (рис. 30.11,б), второй – эти же перемещения от единичного смещения линейной связи (рис. 30.11,в). Поворот узла по часовой стрелке в соответствии с принятым знаком для узловых сосредоточенных моментов считается положительным, знаки же линейных перемещений узлов привязываются к ранее принятой системе координат (рис. 30.13).
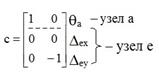
Транспонированная матрица запишется:
После формирования матриц ат, , ст
и F получим матрицу свободных членов
системы канонических уравнений метода перемещений RF.
7. Вычисление элементов матрицы неизвестных метода перемещений по формуле (8.59).
8. Вычисление матрицы концевых усилий в заданной раме по формуле (29).
9. Проверка решения по формуле (33).
т.е. реакции в наложенных связях в основной системе метода перемещений равны нулю, что соответствует заданному состоянию рамы, где эти связи отсутствуют.
10. Построение эпюр внутренних усилий в заданной раме от постоянной нагрузки (рис. 30.14) и временной нагрузки (рис. 30.15).
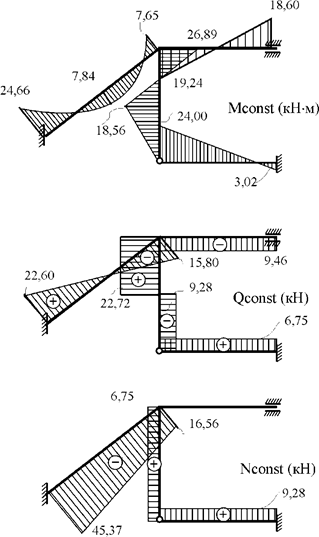
Рис.
30.14
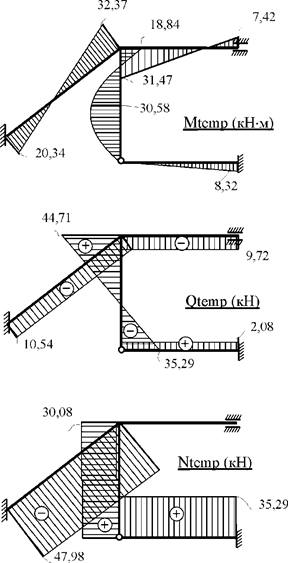
Рис. 30.15
Матрица SF содержит ординаты эпюр изгибающих моментов для всех концевых сечений стержней рамы и ординаты эпюр поперечных сил для сечений 1, 3, 5, 7. Недостающие ординаты эпюр поперечных сил для первого и третьего элементов рамы от постоянной нагрузки и для третьего элемента от временной нагрузки (рис. 30.12) определяются из условий равновесия перечисленных элементов. Ординаты эпюр продольных сил вычисляются из условий равновесия узлов рамы. Вычисление недостающих ординат эпюры Q и построение эпюры N предлагается выполнить самостоятельно.
11. Вычисление расчетных изгибающих моментов и соответствующих им поперечных и продольных сил (см. таблицу ниже).
|
|
Номера концевых сечений |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Mconst |
–7,65 |
–24,66 |
19,24 |
–18,60 |
26,89 |
3,02 |
|
Mtemp |
–32,37 |
20,34 |
31,47 |
–7,42 |
18,84 |
8,32 |
|
Qconst |
–15,80 |
22,60 |
–9,46 |
–9,46 |
22,72 |
6,75 |
|
Qtemp |
–10,54 |
–10,54 |
–9,72 |
–9,72 |
44,71 |
2,08 |
|
Nconst |
–16,56 |
–45,37 |
0 |
0 |
6,75 |
9,28 |
|
Ntemp |
–47,98 |
–47,98 |
0 |
0 |
30,08 |
35,29 |
|
|
– |
– |
50,71 |
– |
45,73 |
11,34 |
|
Qсоотв |
– |
– |
–19,18 |
– |
67,43 |
8,83 |
|
Nсоотв |
– |
– |
0 |
– |
36,83 |
44,57 |
|
|
–40,02 |
–24,56 |
– |
–26,02 |
– |
– |
|
Qсоотв |
–26,34 |
22,60 |
– |
–19,18 |
– |
– |
|
Nсоотв |
–64,54 |
–45,37 |
– |
0 |
– |
– |
|
Примечание. 1. Изгибающие моменты, приведенные в таблице, имеют размерность кНм, поперечные и продольные силы – кН. |
||||||
2. На горизонтальных и наклонном элементах рамы положительными зафиксированы изгибающие моменты, растягивающие нижние волокна, а на вертикальном – изгибающие моменты, растягивающие правые волокна.
3. «Прочерк» в таблице означает, что расчетные изгибающие моменты с указанным знаком («плюс» или «минус») при любых сочетаниях постоянной и временной нагрузки будут отсутствовать. В этом случае теряет смысл вычисление соответствующих поперечных и продольных сил.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Теория машин и механизмов
