Главная
9.2.
Основные определения метода конечных элементов
Метод
конечных элементов (МКЭ) - основной метод современной строительной
механики, лежащий в основе подавляющего большинства современных программных
комплексов, предназначенных для выполнения
расчетов строительных конструкций на ЭВМ.
Но диапазон его применения чрезвычайно широк: строительство и машиностроение, гидро- и аэродинамика, горное дело и новейшая техника, а также различные задачи математической физики – теплопроводности, фильтрации, распространения волн и т. д.
Метод конечных элементов впервые был применен в инженерной практике в начале 50-х гг. XX в. Первоначально он развивался по двум независимым один от другого направлениям – инженерному и математическому. На раннем этапе формулировки МКЭ основывались на принципах строительной механики, что ограничивало сферу его применения. И только когда были сформулированы основы метода в вариационной форме, стало возможным распространение его на многие другие задачи. Быстрое развитие МКЭ шло параллельно с прогрессом современной компьютерной техники и ее применением в различных областях науки и инженерной практики.
Значительный вклад в разработку МКЭ был сделан Дж. Аргирисом. Им впервые дана общая матричная формулировка расчета стержневых систем на базе фундаментальных энергетических принципов, определена матрица податливости, а также введено понятие матрицы жесткости (как обратной матрице податливости). Работы Дж. Аргириса и его сотрудников, опубликованные в период 1954–1960 гг., дали отправную точку для матричной формулировки известных численных методов и применения ЭВМ в расчетах конструкций.
Для развития МКЭ особое значение имели вариационные принципы механики и математические методы, основанные на этих принципах. Дискретизацию задачи на основе вариационного метода Ритца впервые в 1943 г. применил Р. Курант. Лишь в 50-е гг. появились аналогичные работы Ж. Поли, Ж. Герша и др.
Первая работа, в которой была изложена современная концепция МКЭ, относится к 1956 г. Американские ученые М. Тэрнер, Р. Клафф, Г. Мартин и Л. Топп, решая плоскую задачу теории упругости, ввели элемент треугольного вида, для которого сформировали матрицу жесткости и вектор узловых сил. Название – метод конечных элементов ввел в 1960 г. Р. Клафф. В период 1960–1965 гг. опубликованы работы, в которых на основе вариационных принципов получены конечные элементы для решения задач изгиба плит, тонких оболочек, массивов. Среди них можно отметить работы Р. Мак-Лейа, Р. Мелоша, Дж. Бесселина, Ф. де Веубеке, М. Джонса, Т. Пиана. В 1967 г. издана первая монография о МКЭ О. Зенкевича и И. Чанга, в которой изложены основы метода и области его применения.
К семидесятым годам относится появление математической теории конечных элементов. Здесь можно выделить труды И. Бабушки, Р. Галлагера, Ж. Дек-лу, Дж. Одена, Г. Стренга, Дж. Фикса. Значительный вклад в разработку теоретических основ МКЭ внесли и российские ученые. В. Г. Корнеев указал на совпадение математической сущности МКЭ и ВРМ. Сопоставление МКЭ с рядом вариационных методов приведено в трудах Л. А. Розина. Под руководством А. С. Сахарова разработана моментная схема конечных элементов.
Период последних десятилетий особенно характерен для развития и применения МКЭ в таких областях механики сплошных сред, как оптимальное проектирование, учет нелинейного поведения, динамика конструкций и т. п.
Метод конечных элементов, как и многие другие
численные методы, основан на представлении реальной континуальной конструкции ее
дискретной моделью и замене дифференциальных уравнений, описывающих
НДС сплошных тел, системой алгебраических
уравнений. Вместе с тем МКЭ допускает
ясную геометрическую, конструктивную и физическую интерпретацию.
Суть метода заключается в том, что область
(одно- , двух- или трехмерная), занимаемая конструкцией, разбивается на
некоторое число малых, но конечных по размерам подобластей (рис. 9.3). Последние носят название конечных элементов (КЭ), а сам процесс
разбивки – дискретизацией.
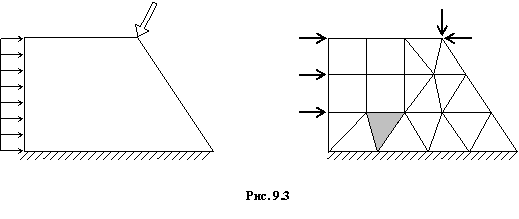
В зависимости от типа конструкции и характера
ее деформации КЭ могут иметь различную форму.
Так, при расчете стержневых систем (фермы, балки,
рамы) КЭ представляют собой участки стержней;
для двумерных континуальных конструкций (пластины, плиты, оболочки) чаще
всего применяют треугольные и прямоугольные (плоские или изогнутые) КЭ; а для трехмерных областей (толстые плиты, массивы) – КЭ в
форме тетраэдра или параллелепипеда.
В отличие от реального сооружения в дискретной модели конечные элементы связываются между собой только в
отдельных точках (узлах) определенным
конечным числом узловых параметров.
МКЭ – это вариационный метод. Функционал энергии для всей рассматриваемой
области здесь представляется в виде суммы функционалов отдельных ее частей – конечных элементов. По области каждого элемента, независимо от
других, задается свой закон распределения искомых функций. Такая кусочно-непрерывная аппроксимация
выполняется с помощью специально подобранных аппроксимирующих функций,
называемых также координатными или интерполирующими. С их помощью искомые непрерывные величины
(перемещения, напряжения и т.д.) в пределах каждого КЭ выражаются через значения
этих величин в узловых точках, а произвольная заданная нагрузка заменяется системой
эквивалентных узловых сил.
При такой кусочно-непрерывной аппроксимации
обеспечивается условие совместности лишь в узлах, а в остальных точках по
границам КЭ это условие удовлетворяется в общем случае приближенно (в связи с
этим различают КЭ разной степени совместности).
Наибольшее распространение получил метод
конечных элементов в перемещениях, имеющий много общего с методом Ритца и вариационно-разностным
методом (в дальнейшем мы будем в основном рассматривать именно этот вариант
МКЭ). Различие между традиционной схемой
метода Ритца и МКЭ в форме метода перемещений заключается в выборе системы
аппроксимирующих функций. Если в методе
Ритца аппроксимация перемещений производится по всей области их определения, то
в МКЭ – по каждому конечному элементу в отдельности, что позволяет использовать
аппроксимирующие функции более простого вида.
В первом случае функционал полной потенциальной энергии варьируется по
неопределенным коэффициентам 
, во втором – по
перемещениям в узлах сетки, что приводит к системе алгебраических уравнений
метода перемещений (основными неизвестными являются непосредственно узловые
перемещения). При этом использование кусочно-непрерывной
аппроксимации позволяет получить редко заполненную или ленточную структуру
матрицы коэффициентов системы уравнений и таким образом дает возможность
применения более эффективных методов ее решения.
Число узлов и число перемещений в узле (степень свободы узла), принятые для
конечного элемента, могут быть различными, однако не должны быть меньше
минимально необходимых для описания напряженно-деформированного состояния КЭ в
рамках принятой физической модели. Число независимых перемещений во всех узлах
элемента определяет степень свободы КЭ. Степень
свободы всей конструкции и
соответственно порядок системы разрешающих уравнений определяется суммарным
числом перемещений всех ее узлов.
Поскольку основными неизвестными МКЭ в форме метода перемещений
считаются узловые перемещения, степень свободы КЭ и всей конструкции в целом
является чрезвычайно важным понятием в МКЭ.
Понятия о степени свободы узла, КЭ и конструкции и степени их же кинематической неопределимости идентичны.
Способ разбивки рассматриваемой области на
конечные элементы, их число и число степеней свободы, а также вид
аппроксимирующих функций в конечном итоге предопределяют точность расчета конструкции.
Следует отметить, что простым увеличением числа конечных элементов не
всегда удается достичь повышения точности расчетов. Вопросы устойчивости и сходимости решения, а
также оценки точности полученных результатов являются основными при использовании
МКЭ.
По сравнению с другими численными методами
МКЭ в лучшей степени алгоритмизирован и более гибок
при описании геометрии и граничных условий рассчитываемой области. Кроме того, к достоинствам метода следует
отнести его физическую наглядность и универсальность.
Применительно к стержневым системам МКЭ в
форме метода перемещений может рассматриваться как матричная форма классического
метода перемещений, отличающаяся только более глубокой формализацией алгоритма
и ориентацией его на использование ЭВМ.
Метод конечных элементов позволяет практически полностью автоматизировать расчет стержневых систем, хотя, как правило, требует выполнения значительно большего числа вычислительных операций по сравнению с классическими методами строительной механики. Однако, в современных условиях большой объем вычислений не является серьезной проблемой, и, в связи с этим, при внедрении ЭВМ в инженерную практику МКЭ получил широчайшее распространение. Поэтому, знание основ метода конечных элементов и современных программных средств, позволяющих на его основе решать разнообразные задачи, в наше время для инженера является абсолютно необходимым.
Виды
МКЭ
По способу получения основных, т. е. разрешающих, уравнений различают четыре основных вида метода конечных элементов: прямой, вариационный, взвешенных невязок и энергетического баланса.
Прямой метод аналогичен матричному методу перемещений для стержневых систем, в основе его лежат положения, которые использовались на ранней стадии развития МКЭ. Этот метод удобен своей простотой и очевидным геометрическо-физическим значением отдельных шагов аппроксимации. Соотношения для КЭ здесь строятся непосредственно на основе трех групп уравнений (трех сторон задачи): статической, геометрической и физической. Однако область применения прямого метода весьма ограничена: его можно использовать лишь для конечных элементов простой геометрии с малым числом степеней свободы в узле.
Вариационный метод основан на принципах стационарности некоторой переменной, зависящей от одной или нескольких функций (такая переменная носит название функционала). Применительно к механике деформируемого твердого тела эта переменная представляет собой потенциальную (функционал Лагранжа) или дополнительную (функционал Кастилиано) энергию системы или формируется на основе этих двух энергий (функционалы Хеллингера-Рейсснера, Ху-Вашицу). Если в функционал подставить аппроксимирующие выражения искомых функций и применить к нему экстремальные принципы (соответственно принцип Лагранжа, принцип Кастилиано и т. д.), получим систему алгебраических уравнений, решением которой будут значения узловых неизвестных. В отличие от прямого вариационный метод может одинаково успешно применяться как к простым, так и сложным задачам.
Метод невязок представляет собой наиболее общий подход к построению основных соотношений МКЭ. Этот метод целесообразно применять при решении задач, у которых трудно или невозможно сформулировать вариационное уравнение, т.е. функционал. Суть метода взвешенных невязок заключается во введении некоторой невязки – отклонении приближенного аппроксимативного решения от точного решения дифференциальных уравнений для данной задачи. Чтобы получить ”наилучшее” решение, необходимо минимизировать некоторый интеграл от невязок по расчетной области. Для повышения эффективности в подынтегральное выражение наряду с самой невязкой обычно вводится так называемая весовая функция, в этом случае метод называется методом взвешенных невязок. Выбор схемы минимизации и весовых функций определяет различные варианты метода невязок. Наиболее часто применяемые из них – это метод Галеркина, который приводит к тем же уравнениям, что и вариационный подход, а также метод наименьших квадратов.
Метод энергетического баланса (метод Одена) основан на балансе различных видов энергии, записанном в интегральной форме. Этот метод успешно применяется при решении нелинейных и динамических задач.
Из приведенных видов МКЭ в строительной механике особенно актуальны вариационный метод и метод взвешенных невязок Галеркина, которые для рассматриваемой задачи представляют собой два взаимно дополняющих метода одинаковой точности. Широкое применение этих методов обусловлено тем, что выражения в функционале или во взвешенном интеграле, как правило, имеют низший порядок производных по сравнению с производными в соответствующем дифференциальном уравнении для данной задачи. Это позволяет выбирать аппроксимирующие функции из более широкого семейства простых функций. Можно сказать, что вариационный вид МКЭ вышел из классического метода Ритца, а метод Галеркина – из обобщенного метода Бубнова-Галеркина. В принципе, из других методов также выводятся соответствующие виды МКЭ, однако их применяют значительно реже.
Формы
МКЭ
В МКЭ, аналогично классическим методам строительной механики, за основные неизвестные могут приниматься величины разного типа: кинематические (перемещения, деформации), статические (внутренние силы, напряжения и др.) или смешанные кинематические и статические параметры. В зависимости от выбора узловых неизвестных различают три формы МКЭ: метод перемещений, метод сил и смешанный метод. С этой точки зрения МКЭ можно рассматривать как обобщение традиционных методов строительной механики стержневых систем применительно к расчету континуальных систем.
Метод перемещений – в настоящее время наиболее распространенная форма МКЭ. Это объясняется тем, что для заданной конструкции легче получить кинематически определимую основную систему метода перемещений, нежели статически определимую основную систему метода сил. Кроме того, матрица жесткости метода перемещений составляется без особых затруднений и, как правило, имеет разряженную или ленточную структуру.
В основе математической формулировки МКЭ в форме метода перемещений лежит вариационный принцип Лагранжа, т. е. принцип минимума потенциальной энергии системы. Основными неизвестными здесь являются перемещения узловых точек дискретной схемы, напряжения же вторичны и определяются путем численного дифференцирования перемещений.
К достоинствам метода относятся: простота реализации; удовлетворительные точность и устойчивость решения с гарантированной сходимостью к нижней границе. Минусы: точность определения напряжений намного ниже, чем перемещений, хотя именно значения напряжений важны при прочностных расчетах, к тому же поскольку приближенное решение отвечает нижней границе, то значения и перемещений, и напряжений оказываются заниженными.
Принцип минимума дополнительной энергии и
связанные с ним схемы МКЭ в форме
метода сил, а также
вариационный
принцип
Рейсснера (смешанный
метод) не получили такого широкого распространения. Однако во многих случаях они могут быть
эффективны, особенно в отношении вычисления напряжений. К тому же выполнение двойственных расчетов на
основе альтернативных форм МКЭ позволяет, как правило, получить двухстороннюю
оценку точного решения соответствующей задачи.
Главным плюсом МКЭ в форме метода сил является то, что основные неизвестные здесь – напряжения. И если бы в реализации метода сил не было определенных сложностей, значения напряжений можно было получать той же степени точности, что и перемещения в методе перемещений. Кроме того, использование принципа Кастилиано дает верхнюю границу приближенного решения (т. е. напряжения завышены), что в принципе лучше при расчетах на прочность, нежели заниженная оценка. Тем не менее, пока нет алгоритмов, в той же степени простых и устойчивых, имеющих гарантированную сходимость в обширном классе задач, подобно МКЭ в форме метода перемещений.
В основе вариационной формулировки смешанного метода лежит принцип стационарности различных форм функционала Рейсснера. При данном подходе перемещения и напряжения в пределах каждого КЭ аппроксимируются одновременно, поэтому нет необходимости завышать требования к непрерывности искомых функций и их производных. Напротив, можно задавать именно нужные аппроксимации, а поскольку смешанные вариационные принципы приводят и к смешанному виду соотношений между напряжениями и перемещениями для конечного элемента, можно получать более точное решение.
Однако имеются и большие минусы. Так, функционал Рейсснера не является выпуклым, поверхность его в точке стационарности имеет вырожденную седлообразную форму. Система разрешающих уравнений, отвечающая формулировке смешанного метода, не является положительно определенной. Эти обстоятельства значительно затрудняют прямое использование функционала Рейсснера в методе конечных элементов.
Также существуют различные гибридные формы как метода перемещений, так и метода сил. По сути гибридные подходы схожи со смешанным методом. Отличает их то, что в гибридных моделях внутри конечного элемента за основные неизвестные принимаются величины одного типа, а на границах элемента независимо и в другой форме – величины другого или же обоих типов.
Как правило, гибридные формулировки приводят к значительному усложнению алгоритма, поэтому эффективны лишь для ограниченного класса задач. Например, если в гибридном методе сил внутри элемента задать аппроксимацию компонент напряжений, в традиционной форме метода сил это бы привело к решению, соответствующему верхней границе. Однако аппроксимация перемещений вдоль контура элемента накладывает некоторые ограничения на математическую модель, уменьшает податливость и тем самым смещает получаемое решение в сторону точного. Сложность в том, что имеется возможность перегрузить ограничениями функционал дополнительной энергии и легко проскочить точное решение в сторону нижней границы.
Аппроксимация
МКЭ относится к методам дискретного анализа. Однако в отличие от численных методов, основывающихся на математической дискретизации дифференциальных уравнений, МКЭ базируется на физической дискретизации рассматриваемого объекта. Реальная конструкция как сплошная среда с бесконечно многим числом степеней свободы заменяется дискретной моделью связанных между собой элементов с конечным числом степеней свободы. Так как число возможных дискретных моделей для континуальной области неограниченно велико, то основная задача заключается в том, чтобы выбрать такую модель, которая лучше всего аппроксимирует данную область.
Сущность аппроксимации сплошной среды по МКЭ состоит в следующем:
1)
рассматриваемая область разбивается на определенное число КЭ, семейство элементов по всей области
называется системой или сеткой
конечных элементов;
2)
предполагается, что КЭ соединяются между собой в конечном числе точек – узлов,
расположенных по контуру каждого из элементов;
3) искомые функции в пределах каждого КЭ (например, распределение перемещений, деформаций, напряжений и т. д.) с помощью аппроксимирующих функций выражаются через узловые значения, представляющие собой основные неизвестные МКЭ;
4) для анализа и расчета полученной системы конечных элементов действительны все принципы и методы, применяемые для любых дискретных систем.
Аппроксимирующие
функции
Аппроксимация, как правило, дает приближенное, а не точное, описание действительного распределения искомых величин в элементе. Поэтому результаты расчета конструкции в общем случае также являются приближенными. Закономерно может быть поставлен вопрос о точности, устойчивости и сходимости решений, полученных МКЭ.
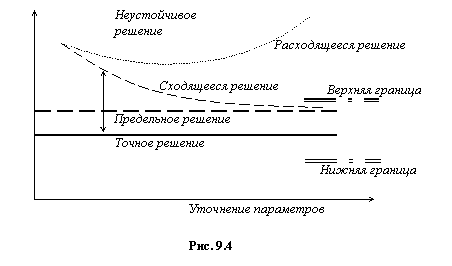
Под точностью понимается отклонение приближенного решения от точного или истинного решения. Устойчивость, прежде всего, определяется ростом ошибок при выполнении отдельных вычислительных операций. Неустойчивое решение является результатом неудачного выбора аппроксимирующих функций, «плохой» разбивки области на КЭ, некорректного представления граничных условий и т. п. Под сходимостью подразумевается постепенное приближение последовательных решений к предельному, по мере того как уточняются параметры дискретной модели, такие как размеры элементов, степень аппроксимирующих функций и т. п. В этом смысле понятие сходимости аналогично тому значению, которое оно имеет в обычных итерационных процессах. Таким образом, в сходящейся процедуре различие между последующими решениями уменьшается, стремясь в пределе к нулю.
Перечисленные выше понятия иллюстрируются рис. 9.4. Здесь абсцисса обозначает степень уточнения параметров дискретной модели, а ордината определяет полученное при этом уточнении приближенное решение. На графике показан монотонный тип сходимости, при котором точность решения повышается плавно.
Ошибки метода конечных элементов
Как следует их вышеизложенного, критерии устойчивости, сходимости и точности в основном определяются погрешностями различного рода операций, проводимых в МКЭ. Наряду с обычными ошибками округления и погрешностью приближенных методов линейной алгебры, применяемых в МКЭ, есть и ошибки, имеющие непосредственное отношение к методу конечных элементов:
– ошибки дискретизации, являющиеся результатом различий между действительной геометрией рассчитываемой области и ее аппроксимацией системой конечных элементов;
– ошибки аппроксимации, обусловленные разностью между действительным распределением искомых функций в пределах КЭ и их представлением с помощью аппроксимирующих функций.
Ошибки дискретизации уменьшаются с увеличением числа
конечных элементов и соответственно с уменьшением их размеров, причем они
стремятся к нулю, когда размер элемента стремится к нулю. Эти ошибки уменьшаются и с применением криволинейных элементов на
соответствующих границах области.
Ошибки аппроксимации не обязательно уменьшаются по мере уменьшения размеров
элементов или повышения степени аппроксимации, поэтому могут ухудшать
сходимость к точному решению или даже приводить
к расходимости. Однако эти ошибки
можно свести к минимуму, если при
построении аппроксимирующих функций обеспечить:
1) непрерывность искомой функции и ее производных в области КЭ до степени m–1 включительно (m – наибольший порядок производных искомой функции, используемых в качестве основных неизвестных в эрмитовых элементах);
2) выполнение условий полноты, т. е. при уменьшении размеров КЭ аппроксимирующие функции должны обеспечить стремление значений искомой функции, а также ее производных к постоянным значениям;
3) выполнение условий совместности искомой функции и частично ее производных на границе между смежными элементами;
4) приближенное удовлетворение условий совместности не основных переменных (например, напряжений, если основные неизвестные – перемещения) на границах КЭ, а также граничных условий в рассматриваемой области;
5) исключение концентрации напряжений в КЭ, если в рассматриваемой области такие концентрации заведомо отсутствуют;
6) при перемещениях КЭ как жесткого целого в нем не должны возникать деформации.
Требование полноты аппроксимирующих функций необходимо для учета смещения КЭ как жесткого целого и обеспечения состояния постоянных деформаций в элементе. Механический смысл совместности заключается в непрерывности основных неизвестных на смежных границах соседних КЭ. В сложных эрмитовых элементах выполнение условий совместности достигается сложнее. Между тем имеются случаи, когда несовместные элементы дают очень хорошие результаты при быстрой сходимости решения к точному.
9.3.
Общий алгоритм статического расчета МКЭ
В принципе общий алгоритм расчета МКЭ сводится к последовательности шагов (матричных операций), в результате выполнения которых определяются необходимые параметры решения задачи (перемещения, деформации, напряжения). На практике расчеты по МКЭ всегда выполняются с применением компьютерных технологий, реализующих известные матричные формулы и выражения для получения промежуточных и конечных результатов.
Ниже приведены основные этапы статического расчета конструкции МКЭ.
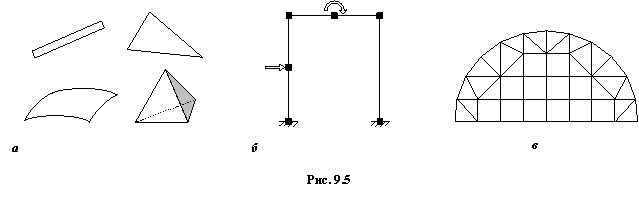
1.Дискретизация конструкции. Рассматриваемая область представляется в виде совокупности конечных элементов, соединенных между собой в узловых точках. Сами элементы могут иметь различную форму и размеры, например, в виде стержня, треугольной пластинки, прямоугольной в плане оболочки, пространственного тетраэдра (рис. 9.5, а). Выбор типа КЭ и общего их числа зависит от вида и формы конструкции, от требуемой точности, от характера внешней нагрузки и наложенных связей. Например, при расчете стержневых систем каждый стержень постоянного сечения принимается за отдельный элемент (рис. 9.5, б). Решение в этом случае получается точным.
Дискретизация континуальных систем (пластины, оболочки, массивы) является более сложной задачей. Общих рекомендаций по нанесению сетки или разбивке области на отдельные элементы нет. Обычно руководствуются предварительными представлениями о характере ожидаемого результата и в местах предполагаемых высоких градиентов искомых величин сетку КЭ сгущают. Однако следует помнить, что применение неравномерной разбивки может вызвать дополнительные трудности, связанные с ухудшением обусловленности системы разрешающих уравнений. Вообще рациональная разбивка требует некоторых практических навыков. Она может быть самой разнообразной. При решении двумерных задач (балка-стенка, изгиб плиты) дискретизация области обычно производится треугольными и прямоугольными элементами (рис. 9.5, в). Предполагается, что вся действующая нагрузка приводится к узловой, поэтому, например, в случае распределенной нагрузки для ее более точного моделирования бывает необходимо вводить дополнительные узлы и элементы. Заданные перемещения, жесткие или упругие связи также должны быть отнесены к узлам.
Таким образом, первый этап заключается в составлении конечно-элементной схемы – дискретной модели конструкции. Здесь можно выделить следующие действия:
а) выбор типа КЭ (по геометрии, виду аппроксимации и т. п.);
б) разбивку области на КЭ (с нумерацией узлов и элементов);
в) описание каждого элемента: топологические (номера узлов в сетке), физико-механические (модуль упругости и т. п.), геометрические характеристики;
г) описание каждого узла (координаты в общей системе координат);
д) описание
заданных узловых нагрузок и перемещений.
Несмотря на то, что перечисленные выше действия не опираются на строгие теоретические рекомендации и во многом выполняются интуитивно, первый этап имеет большое значение для дальнейшего расчета конструкции.
2. Построение глобальных матрицы жесткости и вектора узловых сил. Процедура основана на формировании МЖ и ВН отдельных элементов и их размещении в глобальных МЖ и ВН путем обхода по всем конечным элементам дискретной модели.
Расчеты по МКЭ различных конструкций отличаются принципиально только применяемыми элементными МЖ, ВН и матричными операторами для определения внутренних усилий и напряжений. Данные матрицы и векторы строятся на основе вариационных принципов с учетом принятой геометрии КЭ и выбранных аппроксимаций. В случае если МЖ и ВН конечного элемента построены в локальной (местной) системе координат, не совпадающей с глобальной, необходимо преобразовать их для глобальной системы.
Размещение элементных МЖ (ВН) в глобальной МЖ (ВН) может быть выполнено одним из следующих способов:
1) непосредственного сложения жесткостей;
2) конгруэнтного преобразования;
3) при помощи конечно-разностных операторов.
Способ непосредственного сложения жесткостей, используемый в большинстве случаев, реализуется следующим образом:
– МЖ отдельного элемента представляется в блочной форме, где число блоков (в строке или в столбце) определяется количеством узлов КЭ, размерность каждого блока соответствует числу степеней свободы в узле;
– каждая строка или столбец блочной МЖ элемента соответствует глобальному номеру узла в конечно-элементной модели конструкции;
– глобальная МЖ также представляется в виде блоков, аналогично элементной, число блоков соответствует общему числу узлов дискретной модели;
– МЖ каждого элемента размещается поблочно в глобальной МЖ согласно адресам блоков, т. е. глобальным номерам узлов.
На рис. 9.6 изображена схема размещения МЖ треугольного элемента (три узла, две степени свободы в узле) в глобальной МЖ. Здесь 1, 2, 3 – локальные номера узлов в элементе, i, j, k – глобальные номера узлов.
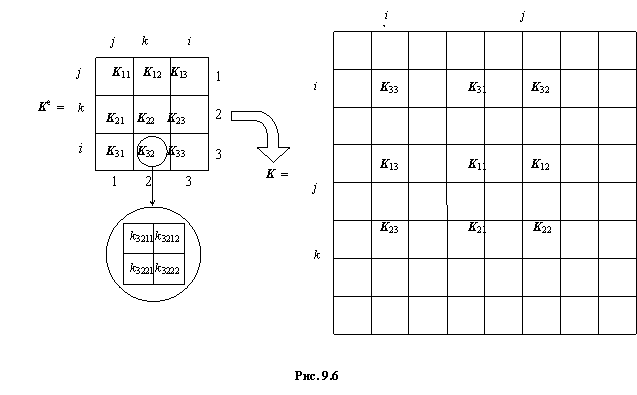
По аналогичной схеме из элементных ВН формируется глобальный ВН для всей конструкции.
Таким образом, данный этап включает следующие основные действия, выполняемые в цикле для каждого из конечных элементов:
а) составление элементных МЖ и ВН в локальной системе координат;
б) преобразование элементных МЖ и ВН из локальной в глобальную систему координат – в том случае, если локальная система не совпадает с глобальной;
в) размещение элементных МЖ и ВН в глобальных МЖ и ВН.
Сформированная на этом этапе МЖ системы является вырожденной или особенной. Она может быть преобразована в невырожденную при учете кинематических граничных условий (внешних связей, наложенных на некоторые узлы и исключающих перемещение конструкции как абсолютно твердого тела).
3. Учет заданных граничных условий. Пусть в результате выполнения второго этапа система разрешающих уравнений имеет вид
K q = P, (9.1)
где глобальная матрица жесткости K содержит коэффициенты kij; вектор узловых перемещений q – компоненты перемещений qi; вектор узловой нагрузки P – узловые силы pi. (i = 1, …, n; j = 1, …, n; n – число степеней свободы системы).
Статические граничные условия учитываются при формировании вектора нагрузки P. Проблема решается просто, если внешние нагрузки заданы непосредственно в узловых точках. Распределенные же нагрузки заменяются эквивалентными обобщенными узловыми силами Pузл, при этом с целью уменьшения погрешности расчета часто приходится разбивать конструкцию на более мелкие элементы. Эти узловые силы добавляются к тем, что получены при формировании (на 2-м этапе) вектора P из элементных нагрузок Pэл:
Pl = Pl эл + Pl узл; (l = 1, … , np),
где np – число компонент узловой нагрузки.
Кинематические граничные условия, как правило, представляются в виде заданных узловых перемещений (равных и не равных нулю). Нулевые перемещения соответствуют абсолютно жестким опорным связям, наложенным на некоторые узлы дискретной модели конструкции. Отличные от нуля заданные перемещения могут быть обусловлены неточностью изготовления (монтажа), регулированием усилий, смещением (осадкой) опор и т. п.
Пусть qm – заданное перемещение по направлению m-й степени свободы (m = 1, … , nq). Тогда корректировка системы уравнений (9.1) может быть произведена следующим образом (в цикле по всем компонентам заданных узловых перемещений nq):
1) из вектора P вычитается m-й столбец матрицы K, умноженный на qm:
pi = pi – kim qm, (i
= 1, … , n);
2) обнуляются m-я строка и m-й столбец матрицы K:
kim = 0; kmi = 0, (i = 1, … , n);
3) m-й коэффициент главной диагонали принимается равным единице: kmm = 1;
4) m-ю компоненту вектора P следует положить равной qm, т. е. pm = qm.
Если заданное перемещение qm 
0, то выполняются все
перечисленные пункты, если qm = 0 –
выполняются только 2, 3 и 4-й пункты. Во
втором случае также можно вычеркнуть m-ю строку и
m-й столбец из матрицы K и m-ю компоненту из векторов P и q, тем самым уменьшив
размерность системы алгебраических уравнений МКЭ на число компонент заданных
смещений – nq.
Помимо жестких связей и смещений опор в реальной конструкции могут иметь место упругие связи (упругое основание). Наиболее простой является дискретная модель основания, когда упругие связи приложены в отдельных узлах. В этом случае к МЖ всей системы просто добавляется диагональная матрица, состоящая из коэффициентов жесткости упругих связей:
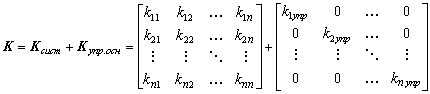. (9.2)
Учет распределенного упругого основания будет более точным, если при его дискретизации использовать вариационные принципы (например, принцип Лагранжа). При таком подходе для каждого конечного элемента, подобно МЖ, строится так называемая матрица реакций основания. Последняя добавляется к МЖ элемента, и далее расчет производится в обычном порядке.
Последовательность действий при учете заданных граничных условий:
а) замена произвольной внешней нагрузки на эквивалентные узловые силы и добавление их в глобальный ВН;
б) дополнение МЖ при учете заданного упругого основания;
в) корректировка глобальной системы уравнений (МЖ и ВН) при учете заданных ненулевых смещений узлов;
г) преобразование глобальной системы уравнений при учете жестких опорных связей (нулевых перемещений).
В результате учета граничных условий глобальная система разрешающих уравнений будет сформирована в окончательном и в то же время достаточном для получения искомого решения виде.
4. Решение системы разрешающих уравнений. Окончательная система разрешающих уравнений МКЭ для статической задачи представляет собой систему линейных алгебраических уравнений с симметричной, положительно определенной матрицей коэффициентов, как правило, ленточной структуры.
Прежде всего следует выбрать метод решения СЛАУ. Для небольших и средних задач – от несколько десятков до несколько десятков тысяч неизвестных – обычно используются известные прямые методы: Гаусса, разложения Холесского, LDLT–факторизации и т. п. Для более сложных систем, требующих огромного объема вычислений и значительной памяти, приходится искать и, если необходимо, создавать специально подходящие для данной задачи эффективные алгоритмы, основанные как на прямых, так и на итерационных методах. Помимо перечисленных, для решения систем разрешающих уравнений МКЭ эффективны такие прямые методы, как метод быстрого преобразования Фурье, методы Гивенса, Хаусхолдера, блочного разложения. В ряде случаев целесообразно применять методы, учитывающие разреженность матриц, а также плохую обусловленность систем уравнений.
Касаясь итерационных методов, отметим следующее. Классические из них – методы Якоби, Гаусса-Зейделя, несмотря на сравнительную простоту, при решении даже средних задач характеризуются крайне медленной сходимостью. Более эффективными (в которых при меньшем числе итераций достигается такая же точность решения) являются следующие итерационные методы: метод последовательной верхней релаксации (модификация процедуры Гаусса-Зейделя с ускорением сходимости), некоторые градиентные методы, в частности, сопряженный метод Ньютона, метод Шелдона, а также ряд блочных итерационных методов.
Можно применять и комбинированные подходы. Так, точность решения, полученного прямым методом, может быть значительно улучшена с помощью дополнительных вычислений, называемых итерационным уточнением.
Отметим некоторые особенности, присущие системе разрешающих уравнений МКЭ. Эти особенности могут значительно влиять на точность получаемого решения, объем вычислений и режим работы вычислительной техники.
Во-первых, при рациональной нумерации узлов матрица коэффициентов СЛАУ имеет ленточную структуру. Это означает, что ненулевые коэффициенты матрицы содержатся только в пределах некоторой полосы – ленты, занимающей диагональное положение в матрице (рис. 9.7).
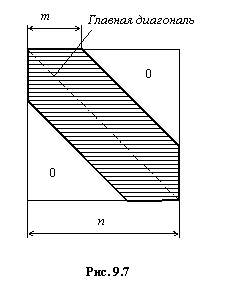
Внутри ленты могут находиться и нулевые коэффициенты. Важным моментом является то, что область нулевых элементов матрицы, расположенная выше и ниже ленты, остается нулевой и в процессе решения системы уравнений. Очевидно, что с уменьшением ширины ленты уменьшается и объем производимых вычислений. Ширина ленты определяется по формуле
m = (rmax + 1) ns.
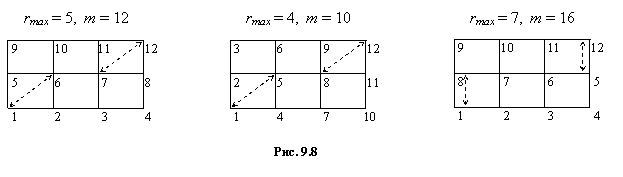
Здесь rmax – величина наибольшей разности между глобальными номерами узлов в пределах каждого КЭ, определяемая при обходе по всем элементам системы; ns – число степеней свободы узла. Для уменьшения ширины ленты следует стремиться к оптимальной нумерации узлов, при которой параметр rmax принимает минимальное значение. Пример разбивки двумерной области на прямоугольные элементы с разными вариантами нумерации узлов приведен на рис. 9.8. Рациональная нумерация узлов дает m = 10, а нерациональная – m = 16 (при ns = 2).
Во-вторых, при решении больших СЛАУ (свыше тысячи уравнений) важным фактором является значительное накопление ошибок округления, возникающих в процессе огромного количества арифметических операций.
Так, например, при использовании метода Гаусса число умножений примерно равно 1/3mn2, где n – порядок системы, m – ширина «ленты». В этом случае уже при нескольких сот уравнений рекомендуется применять двойную точность вычислений (16 знаков после запятой), иначе следует считаться с неизбежной погрешностью получаемого решения.
Основная доля задач в строительстве (исключение составляют крупные сооружения, сложные и ответственные в инженерном плане конструкции и т. п.) относится к задачам средней технической сложности, для которых, как уже было сказано выше, используются прямые методы решения систем уравнений. К тому же при практических расчетах часто бывает необходимо учитывать различные виды нагрузок, к примеру, собственный вес, временную нагрузку от кранового и другого оборудования, снеговую и ветровую нагрузки и т. д. Решение системы уравнений по каждому виду загружения также удобнее всего выполнять с помощью прямых методов. Такое утверждение основывается на том, что любой из прямых методов можно представить в виде двух независимых процедур:
а) приведения матрицы коэффициентов СЛАУ к
треугольному виду посредством последовательных исключений или же факторизацией
(разложением исходной матрицы на
несколько треугольных);
б) решения систем с треугольными матрицами коэффициентов
для каждого вектора нагрузки – вида загружения.
5. Определение внутренних усилий (напряжений). Результатом решения системы разрешающих уравнений МКЭ в форме метода перемещений будут компоненты узловых перемещений дискретной модели конструкции.
Вычисление же необходимых компонент напряженного состояния конструкции производится поэлементно в следующем порядке:
а) формируется вектор узловых перемещений для каждого конечного элемента qe (посредством выборки из глобального вектора узловых перемещений q соответствующих компонент);
б) если локальная система координат для отдельного КЭ не совпадает с глобальной, производится преобразование вектора узловых перемещений qe данного элемента;
в) на основе геометрических и физических соотношений формируется матрица усилий (напряжений) для КЭ – G;
г) вычисляется вектор узловых значений внутренних усилий (напряжений) для КЭ – S e, который связан с узловыми перемещениями в общем случае следующим соотношением:
S e = G q e.
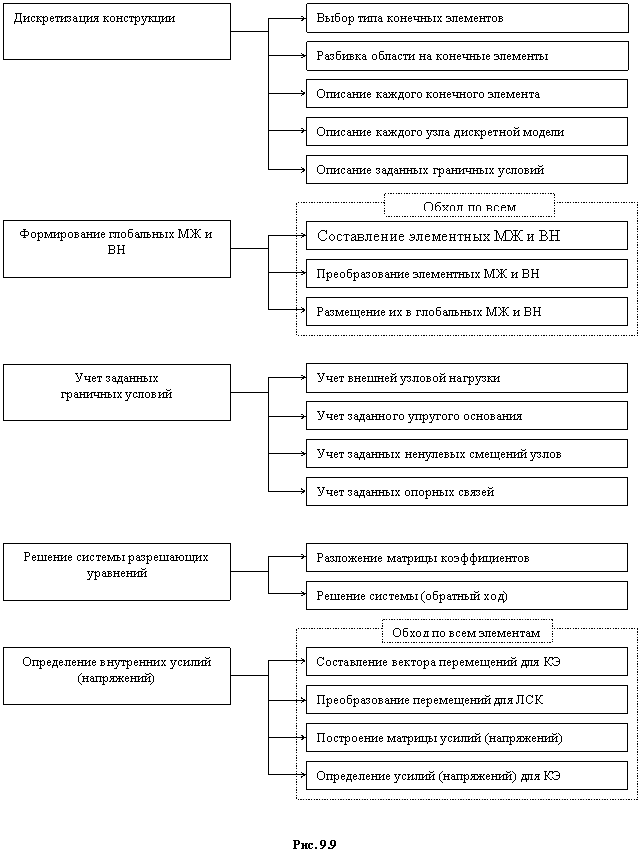
Основные этапы статического расчета конструкций МКЭ и последовательность их выполнения приведены в виде схемы на рис. 9.9.
Понятие о суперэлементном подходе
Сложная структура современных инженерных сооружений: многоэтажных высотных зданий, производственных объектов и т. д., с одной стороны, и стремление к использованию все более точных дискретных схем, с другой стороны, приводят к системам разрешающих уравнений очень большого порядка. Несмотря на то, что современные вычислительные средства и имеющиеся алгоритмы позволяют решать такие системы, возникают определенные трудности с хранением глобальной матрицы жесткости, с точностью решения из-за накопления ошибок округления при огромном числе арифметических операций, с большими затратами «ручного» труда при подготовке исходной информации для расчета и значительными затратами машинного времени.
Разделение системы разрешающих уравнений МКЭ на несколько систем меньшего порядка может быть выполнено уже на этапе построения конечно-элементной модели. Это достигается с помощью введения в дискретную модель конструкции так называемых суперэлементов (СЭ). СЭ – это укрупненный элемент, включающий в себя некоторую группу обычных (базисных) конечных элементов. Суперэлементы обычно повторяют форму и размеры естественных частей реальных конструкций и сооружений: этажи и фрагменты зданий, блоки корпусов, различные конструктивные части сооружений. В основе объединения базисных элементов в СЭ лежит процедура конденсации, применяемая здесь для исключения неизвестных во внутренних узлах суперэлемента.
9.4.
Применение МКЭ при расчете стержневых систем
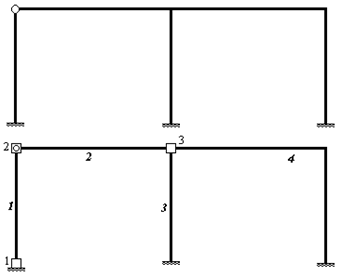
Рис.9.10
В МКЭ стержневая система мысленно разбивается на отдельные части - конечные элементы, соединяющиеся между собой в узлах (рис.9.10). Узлы могут быть жесткими и шарнирными. Совокупность соединенных между собой и прикрепленных к основанию конечных элементов образует расчетную схему метода, называемую конечно-элементной схемой или конечно-элементной моделью или просто системой элементов. Элементы и узлы конечно-элементной схемы нумеруются.
Внешняя нагрузка считается приложенной только в узлах конечно-элементной схемы. В общем случае переход от заданной нагрузки к узловой осуществляется следующим образом. На основании принципа суперпозиций рассматриваемое состояние стержневой системы может быть представлено как сумма двух состояний (рис.9.11). В первом состоянии (задача 1) вводятся связи, препятствующие всем возможным смещениям узлов системы, аналогично тому, как образуется основная система в методе перемещений. При этом, однако, продольными деформациями стержней не пренебрегают. От действия заданных нагрузок во введенных связях возникают реакции. Во втором состоянии (задача 2) узлы конечно-элементной схемы не закреплены от смещений, но к ним прикладываются усилия равные по модулю реакциям в связях, определенным в первом состоянии, но противоположные им по направлению (рис.9.11). Расчет системы в первом состоянии не представляет труда. В частности, если конечно-элементная схема создается таким образом, чтобы элементы представляли собой отдельные стержни (элементы 1, 2 и 3 на рис.9.11), то для каждого из таких элементов имеется табличное решение, позволяющее определить реакции в связях и построить эпюры внутренних усилий по их длине. Для расчета же системы во втором состоянии, т.е. для решения задачи 2, и применяется метод конечных элементов. Окончательное решение задачи будет представлять собой сумму решений этих двух задач.
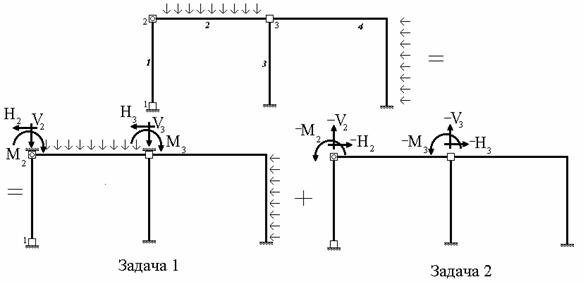
Рис.9.11
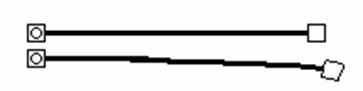
Рис.9.12
В задаче 2 усилия, действующие на любой элемент приложены исключительно в узлах. В этом случае перемещения узлов любого элемента, взятого в отдельности (рис.9.12), однозначно определяют усилия и перемещения в любой точке этого элемента. Как известно, для стержневых систем решение такой задачи может быть найдено точно.
Каждый, взятый отдельно от системы, конечный элемент должен быть достаточно простым, чтобы имелась возможность легко определить перемещения и усилия в любом сечении стержней элемента по заданным перемещениям его узлов. Связь между перемещениями узлов элемента и усилиями в них задается при помощи матрицы жесткости элемента. Количество перемещений узлов элемента, которые однозначно определяют состояние данного элемента называют числом степеней свободы элемента. Оно определяется по формуле:
(9.3)
где 
-число шарнирных узлов в элементе, а 
- число жестких узлов в элементе. Действительно, если узел
представляет собой шарнир, то его положение на плоскости можно охарактеризовать
двумя линейными перемещениями, например в вертикальном и горизонтальном
направлениях. В случае жесткого узла необходимо еще дополнительно к линейным
смещениям задать его поворот.
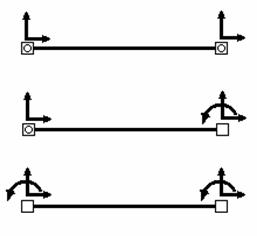
Рис.9.13
На рис.9.13 первый элемент характеризуется четырьмя степенями свободы, т.к. он содержит два шарнирных узла. При отсутствии нагрузки, кроме приложенной в самих узлах, положение на плоскости любой точки этого элемента определяется четырьмя параметрами - двумя вертикальными и двумя горизонтальными перемещениями узлов элемента. У второго элемента на рис.9.9 - пять степеней свободы - к четырем линейным смещениям добавляется поворот в одном из узлов. У третьего элемента - шесть степеней свободы, которым соответствуют четыре линейных и два угловых перемещения.
Аналогично, для всей конечно-элементной схемы
вводятся матрица жесткости системы или глобальная
матрица жесткости, устанавливающая связь между перемещениями узлов системы
и усилиями в них, а также число степеней
свободы системы или глобальное число
степеней свободы - количество
перемещений узлов системы, которые достаточно знать, чтобы однозначно
определить состояние всей системы. Оно также определяется по формуле (9.3), в
которой -число шарнирных узлов, а - число жестких узлов во всей конечно-элементной схеме.
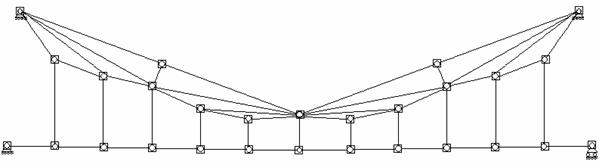
Рис.9.14
Например, конечно-элементная схема висячей системы, изображенной на рис.9.14 содержит в себе 28 шарнирных узлов, следовательно характеризуется 56 степенями свободы.
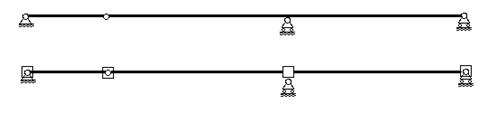
Рис.9.15
В конечно-элементной схеме балки (рис.9.15) используется один жесткий и три шарнирных узла. Следовательно, в соответствии с (9.3) эта схема характеризуется 3×2+1×3=9 степенями свободы.
Для всех элементов, из которых состоит конечно-элементная схема, должны быть построены матрицы жесткости элементов. В программных комплексах, реализующих алгоритм метода конечных элементов, хранятся готовые матрицы жесткости для элементов различных типов.
На практике, при расчете плоских стержневых систем используют готовые матрицы жесткости для элементов только трех типов: простых стержней с двумя жесткими узлами, двумя шарнирными узлами, одним жестким и одним шарнирным узлом (рис.913). В этом случае при разбивке стержневой системы на элементы узлы вводятся в местах соединения и изломов стержней, в опорах, шарнирах и на свободных концах консольных стержней. В принципе узел может быть введен и в любых других точках, например, в точках приложения сосредоточенных сил.
В учебных целях могут использоваться и элементы других типов (рис.9.16), в том числе и включающие в себя опорные закрепления.
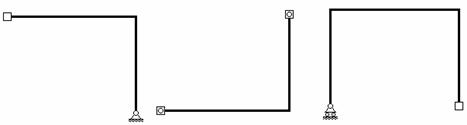
Рис.9.16
Из построенных матриц жесткости элементов формируется матрица жесткости системы. Для этого все матрицы жесткости элементов и матрица жесткости системы должны быть сформированы в единой системе осей координат, называемой глобальной системой осей координат. При расчете плоских стержневых систем традиционно используется следующая глобальная система осей координат (рис.9.17): ось 1 направлена вправо, ось 2 - вверх, ось 3 - против часовой стрелки.
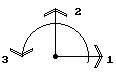
Рис.9.17
Матрицы жесткости элементов могут формироваться и храниться в памяти ЭВМ в своих, локальных системах осей координат, в общем случае отличных от глобальной системы осей координат. В данной ситуации при помощи специальной процедуры эти матрицы должны быть перестроены для глобальной системы осей координат.
Так как матрица жесткости системы устанавливает связь между усилиями, приложенными к ее узлам и перемещениями ее узлов, то имея построенную матрицу жесткости системы и зная внешнюю узловую нагрузку, можно найти перемещения всех узлов конечно-элементной схемы. Для этого требуется решить систему линейных алгебраических уравнений. Порядок этой системы равен числу ее степеней свободы.
По известным перемещениям узлов системы для каждого элемента при помощи имеющихся матриц жесткости элементов можно найти внутренние усилия в элементах от действия нагрузки, приложенной в узлах (задача 2). Окончательное решение задачи, как уже упоминалось, ищется как сумма решений задачи 1 и задачи 2.
Таким образом, метод конечных элементов в данном виде аналогичен методу перемещений, так как сначала определяются перемещения узлов системы, а затем по ним - деформации и усилия в стержнях. Возможна реализация метода конечных элементов и в форме метода сил, однако она имеет ряд существенных недостатков и поэтому представляет большей частью чисто научный, но не практический интерес.
Итак, расчет стержневой системы методом конечных элементов в форме метода перемещений состоит из следующих этапов:
1.Создание конечно-элементной схемы (разбивка системы на элементы и их нумерация).
2.Сведение заданной внешней нагрузки к узловой.
3.Формирование матриц жесткости всех элементов системы в локальных системах координат и их преобразование в глобальную систему координат.
4.Формирование глобальной матрицы жесткости, системы уравнений метода конечных элементов и ее решение.
5.Определение усилий в элементах от действия узловой нагрузки.
6.Определение окончательных значений усилий в элементах путем сложения решений задач 1 и 2.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
