Главная
9.5.
Понятие о конечных элементах
Как было отмечено, метод конечных элементов представляет собой наиболее распространенный приближенный метод в механике твердого тела и может быть интерпретирован с физической или математической точки зрения.
Основа физической концепции МКЭ – это разбиение математической модели конструкции на непересекающиеся компоненты (подобласти) простой геометрии, называемые конечными элементами или просто элементами для краткости. Множество элементов, на которые разбита конструкция, называется конечно-элементной сеткой. Механическое поведение каждого элемента выражается с помощью конечного числа степеней свободы или значений искомых функций во множестве узловых точек. Поведение математической модели, таким образом, аппроксимируется поведением дискретной модели, полученной путем сборки или ансамблирования всех элементов. Заметим, что концепция разбиения-сборки естественно возникает при исследовании многих искусственных или живых систем. Например, легко представить мост, здание, двигатель или скелет, как сложную систему, составленную из простых компонентов. Заметим также, что в отличие от метода конечных разностей, конечные элементы не накладываются друг на друга в пространстве.
9.5.1.
Атрибуты элемента
Рассмотрим основные типы конечных элементов и их свойства, называемые атрибутами элементов (Рис. 9.14).
Рис. 9.14. Основные типы конечных элементов для одно-, дву- и трехмерных задач механики.
Собственная размерность. Конечные элементы могут описываться одной, двумя или тремя пространственными координатами в зависимости от размерности задачи, для решения которой они предназначены. Соответствующее число внутренних или локальных координат называется собственной размерностью элемента. В динамическом анализе время рассматривается как дополнительная размерность. Отметим, что в расчетах используются также специальные элементы с нулевой размерностью, такие как, точечные массы или сосредоточенные упругие элементы (пружины).
Узловые точки. Каждый элемент описывается множеством характерных точек, называемых узловыми точками или узлами для краткости. Узлы предназначены для описания геометрии элемента и для задания физических степеней свободы (числа неизвестных функций). Узлы обычно находятся в угловых или крайних точках элемента, но могут быть также расположены между угловыми узлами и внутри элемента. Данное различие связано с порядком аппроксимации, который обеспечивает данный конечный элемент. Элементы, имеющие только угловые узлы, называются линейными и обеспечивают линейную интерполяцию геометрии и функций. Элементы, имеющие дополнительные узлы на своих границах между угловыми точками, могут обеспечивать квадратичную или даже кубичную интерполяцию (Рис. 9.14). В первом случае такие элементы называются квадратичными. Отметим также, что существуют элементы, имеющие внутренние узлы. Теоретически такие элементы обеспечивают более точное описание геометрии тела и искомых функций, однако широкого распространения данный тип элементов не получил. При наличии современных автоматических генераторов конечно-элементных сеток часто бывает проще и удобнее разбить конструкцию на большое число линейных элементов простой формы, чем использовать элементы высокого порядка, требующие для построения сетки значительной работы вручную. Элементы, не имеющие внутренних узлов, относятся к так называемому серендипову семейству.
Геометрия элемента. Геометрия элемента определяется расположением узловых точек. Большинство элементов, используемых в расчетах, имеют достаточно простую геометрическую форму. Например, в одномерном случае элементы обычно представляют собой прямолинейные отрезки или сегменты кривых линий; в двумерном случае элементы имеют трехстороннюю или четырехстороннюю форму; в трехмерных задачах наиболее распространены такие геометрические фигуры, как тетраэдры, призмы и гексаэдры (Рис. 9.14).
Степени свободы. Степени свободы определяют физическое состояние элемента, т.е. физическое поле, которое описывает данный элемент. Благодаря общим степеням свободы в соседних элементах осуществляется сборка модели и формирование глобальной системы конечно-элементных уравнений. В качестве степеней свободы могут фигурировать как узловые значения неизвестной функции, так и ее производные по пространственным координатам в узлах. В первом случае элементы относятся к типу лагранжевых элементов; во втором случае – типу эрмитовых элементов. Например, в простейшей задаче о растяжении стержня неизвестной функцией является продольное перемещение стержня. Соответственно в качестве степеней свободы выступают узловые значения данной функции и, следовательно, конечный элемент относится к лагранжевому типу. Наоборот, в задаче об изгибе стержня неизвестной функцией является поперечное перемещение центральной оси стержня, а в качестве степеней свободы используются как узловые значения самой функции, так и ее производной по продольной координате. Физический смысл этой производной – угол поворота поперечного сечения стержня. Таким образом, конечный элемент, применяемый в расчетах стержня на изгиб, относится к типу эрмитовых элементов. Заметим также, что данные обозначения происходят от названия полиномов Лагранжа и Эрмита, широко используемых в прикладной математике для интерполяции функций по узловым значениям.
Узловые силы. Система узловых сил полностью соответствует степеням свободы элемента и выражается с помощью глобального вектора узловых сил.
Определяющие соотношения. Для
конечных элементов, используемых в механических расчетах, определяющее
соотношение задает поведение материала, из которого изготовлена конструкция.
Например, в качестве такого соотношения во многих случаях используется
обобщенный закон Гука, связывающий тензор деформаций и тензор напряжений в
точке. Для линейного упругого стержневого элемента
достаточно задать один модуль Юнга Е и один коэффициент
температурного расширения 
.
Свойства сечения. К свойствам сечения относятся площади и моменты инерции одномерных и двумерных конечных элементов, таких как балки, стержни, пластины. В эту группу также входит толщина пластин и оболочек. При построении конечного элемента свойства сечений считаются заданными и входят в результирующую матрицу жесткости элемента.
9.5.2.
Классификация конечных элементов, используемых в механике
Простейшие конструкционные элементы. К простейшим структурным элементам относятся элементы типа стержень, балка, труба, брус, панель, работающая на сдвиг (Рис. 9.15). Уравнения, описывающие данные элементы, выводятся из теоретических положений сопротивления материалов, т.е. из упрощенных механических формулировок. Исторически первыми стали использоваться именно эти типы конечных элементов.
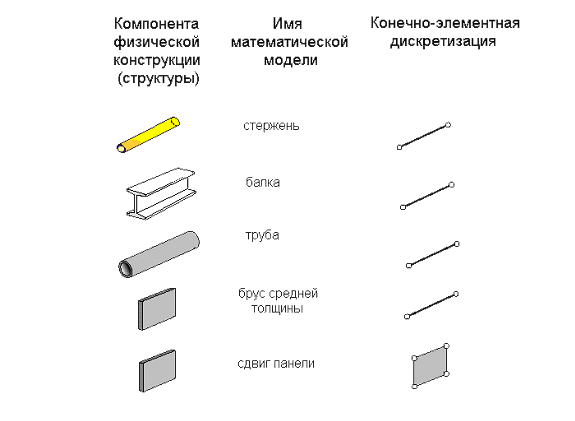
Рис. 9.15. Простейшие конструкционные элементы
Континуальные элементы. Континуальные элементы представляют собой конечные объемы или площади сплошной среды (континуума). Например, к континуальным элементам относятся пластины, оболочки, осесимметричные элементы, трехмерные твердотельные элементы (Рис. 9.16). Уравнения, описывающие данный тип конечных элементов, получаются из общих соотношений механики сплошной среды и, в частности, теории упругости.
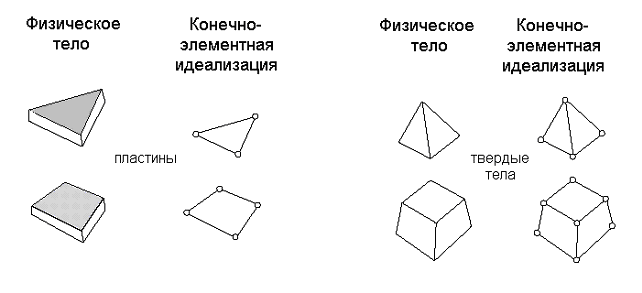
Рис. 9.16. Континуальные конечные элементы.
Специальные элементы. Специальные элементы обладают свойствами как конструкционных, так и континуальных элементов. Они выводятся из уравнений механики сплошной среды, но включают в себя некоторые особенности непосредственно связанные с физическими особенностями решаемых задач. В качестве примера можно привести следующие специальные элементы: элемент с трещиной для задач механики разрушения; многослойная панель; бесконечные и полубесконечные элементы; контактные и штрафные элементы; абсолютно твердотельные элементы (Рис. 9.17).
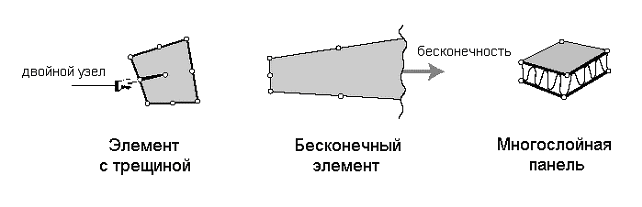
Рис.9.17. Специальные конечные элементы.
Макроэлементы. Макроэлементы представляют собой более сложный тип конечных элементов. Как правило, они получаются путем сборки из более простых конструкционных элементов. Число таких элементов, входящих в макроэлемент, как правило, невелико (Рис. 9.18).
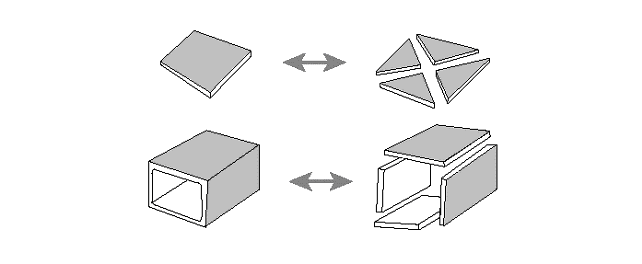
Рис.9.18. Макроэлементы
Подструктуры. Подструктуры можно определить как макроэлементы с явно выраженными структурными особенностями или функциями. Как правило, они получаются путем разделения полной конструкции на функциональные компоненты. Например, крылья и фюзеляж самолета, пролет и тросы подвесного моста. Заметим, что различия между понятиями полной конструкции, подструктур и макроэлементов не всегда очевидны и четко определены. Поэтому часто используется понятие суперэлемента как обобщенного названия для всех типов макроэлементов или подструктур, представляющих собой комбинацию простейших конструкционных элементов.
9.5.3.
Ансамблирование
Ансамблирование или сборка представляет собой объединение отдельных элементов в конечно-элементную сетку. С математической точки зрения ансамблирование состоит в объединении матриц жесткости отдельных элементов в одну глобальную матрицу жесткости всей конструкции. При этом существенно используются две системы нумерации узлов элементов: локальная и глобальная. Локальная нумерация представляет собой фиксированную нумерацию узлов для каждого типа конечных элементов в соответствии с введенной локальной системой координат на элементе. Глобальная нумерация узлов всей конструкции может быть совершенно произвольной, также как и глобальная нумерация конечных элементов. Однако, между локальными номерами и глобальными номерами узлов существует взаимнооднозначное соответствие, на основе которого и формируется глобальная система конечно-элементных уравнений.
9.5.4.
Граничные условия
Согласно терминологии математической физики, рассматривающей различные дифференциальные уравнения, описывающие физические поля, с единой математической точки зрения, граничные или краевые условия для данных дифференциальных уравнений делятся на два основных типа: существенные и естественные. Обычно, существенные условия накладываются на искомую функцию, а естественные на ее производные по пространственным координатам. В математической физике естественные граничные условия получаются «естественным» образом вместе с исходными дифференциальными уравнениями (уравнениями Эйлера) из соответствующего вариационного принципа, в то время как существенные граничные условия должны выполняться независимо.
С позиции метода конечных элементов существенные граничные условия – это такие, которые непосредственно влияют на степени свободы модели и накладываются на компоненты глобального вектора неизвестных U. Наоборот, естественные граничные условия – это такие, которые опосредованно влияют на степени свободы через глобальную систему конечно-элементных уравнений и накладываются на правую часть системы – вектор F.
В задачах механики, как правило, к существенным граничным условиям относят те, которые включают в себя перемещения (но не деформации, представляющие собой производные перемещений по пространственным координатам). Согласно терминологии теории упругости такие граничные условия называются кинематическими. Например, заделка и шарнирное опирание в стержневых задачах представляют собой существенные, или кинематические, граничные условия, наложенные на прогиб или продольные перемещения точек стержня. Заметим, что в задаче изгиба стержня к существенным условиям относится также условия, наложенные на первую производную по продольной координате от прогиба стержня, которая имеет механический смысл угла поворота сечения стержня. Тоже можно сказать об углах поворота сечений в теории изгиба пластин.
К естественным граничным условиям в механических приложениях МКЭ относят условия, наложенные на различные внешние силовые факторы, действующие на точки поверхности тела – сосредоточенные силы и моменты в стержневых задачах; распределенные силы в двумерных и трехмерных задачах. Такие ограничения носят название силовых граничных условий.
В постановках задач механики сплошной среды, и в частности теории упругости, широко используются смешанные граничные условия. Это означает, что в данной точке поверхности тела одновременно заданы некоторые компоненты перемещений и поверхностных сил. Например, такие условия возникают при решении геометрически симметричных задач. Если остальные граничные условия и внешние силы также зеркально симметричны относительно некоторой плоскости, то смешенные граничные условия на плоскости симметрии представляют собой равенство нулю нормальных перемещений и равенство нулю касательных сил.
Перечисленные три варианта граничных условий наиболее распространены в чисто механических приложениях МКЭ. Однако, в междисциплинарных приложениях МКЭ, и в частности, при расчете температурных напряжений, граничные условия накладываются на различные физические переменные и зависят от особенностей математической постановки соответствующих задач.
9.5.5.
Стержневой конечный элемент. Матрица жесткости конечного элемента
Рассмотрим произвольный конечный элемент с числом степеней свободы nст.
Вектором узловых перемещений конечного элемента называется вектор, складывающийся из значений перемещений его узлов по направлению всех его степеней свободы. Очевидно, размерность вектора узловых перемещений равна числу степеней свободы элемента nст.
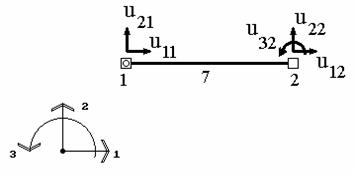
Рис.9.19
Например,
для двухузлового элемента, имеющего в
конечно-элементной схеме номер 7, характеризующегося тремя степенями свободы
(рис.9.19), вектор узловых перемещений будет иметь следующий вид: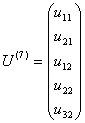 
.
Здесь введены следующие обозначения: 
- перемещение узла k по направлению j, 
-вектор узловых перемещений узла е. Понятно, что если узел k шарнирный, то j может быть равно 1 или 2. Если же узел k жесткий, то j может быть равно 1, 2 или 3.
Аналогично
вводится вектор узловых усилий, действующих на элемент. Его компонентами
являются усилия, приложенные к элементу в узлах и действующие по направлению
всех его степеней свободы. Для приведенного на рис.9.19 элемента этот вектор
будет иметь вид (рис.9.20):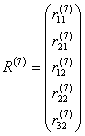 
.
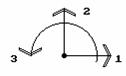
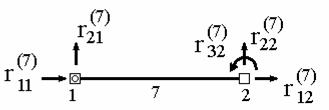
Рис.9.20
Здесь вводятся обозначения: 
- усилие, действующее
на узел k
элемента е по направлению j, 
- вектор узловых сил, действующих на элемент е.
Вектора R(e) и U(e) являются блочными,
т.е. в них можно выделить блоки 
и 
соответственно,
содержащие усилия и перемещения, относящиеся к i-ому узлу элемента.
Если узел i - жесткий, то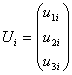 
, если шарнирный, то 
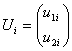. Аналогично выглядят и блоки вектора R(e).
Например, для рассматриваемого элемента (рис.9.19 и рис.9.20):
, 
.
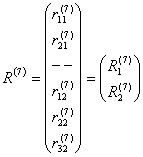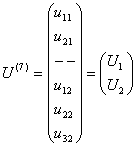Понятно, что при деформировании элемента в результате смещения одного из его узлов по направлению одной из степеней свободы на узлы элемента должны действовать внешние силы, препятствующие возвращению элемента в недеформируемое состояние. Подобная ситуация может возникнуть, например, при неравномерных осадках в опорах статически неопределимой стержневой системы (рис.9.21), реакции, возникшие в опорах, препятствуют возвращению конструкции в недеформированное состояние.
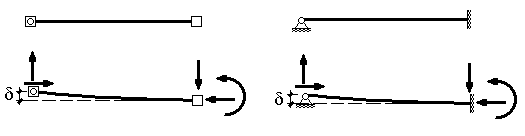
Рис.9.21
В рамках гипотезы линейного деформирования связь между перемещениями узлов элемента и силами, действующими при этом на него, должна быть линейной. Например, с увеличением смещения d вдвое, все усилия, действующие на узлы элемента также должны увеличиться вдвое.
Основной характеристикой конечного элемента
является матрица жесткости элемента 
. Она связывает вектор узловых перемещений и вектор приложенных к элементу узловых усилий соотношением:
,
(9.4)
выражающим линейный характер связи между действующими на
узлы силами и узловыми перемещениями. Матрица жесткости элемента играет роль,
аналогичную коэффициенту жесткости пружины К, связывающего приложенное к ней
усилие R, и вызванное этим усилием
перемещение U соотношением (рис.9.22)
.
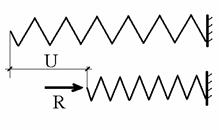
Рис.9.22
Поскольку вектора и имеют размерность 
, число строк и столбцов в матрице тоже должно быть равным :
.
Введем обозначение 
- усилие, действующее на узел m элемента e по направлению i, от единичного
перемещения узла k
этого же элемента е
по направлению j при условии, что перемещения по направлению всех остальных
степеней свободы в элементе равны нулю. Например, 
- усилие, действующее
на узел 1 элемента 5 по направлению 1 при
единичном перемещении узла 2 этого же элемента 5 по направлению 3, а 
- усилие, действующее
на узел 1 элемента 3 по направлению 1 от единичного смещения этого же узла по
этому же направлению. Последнее значение, как и любое значение 
в соответствии с
теоремой Клапейрона всегда положительно, аналогично
коэффициентам 
в уравнениях
классического метода перемещений.
Важно четко помнить порядок индексов, стоящих при k. Верхний индекс - это номер элемента. Первые два нижних индекса - направления, причем первый из них - номер направления определяемого усилия, а второй - номер направления, в котором произошло единичное перемещение. Вторые два нижних индекса - номера узлов элемента, причем первый из них - номер узла, в котором определяется усилие, второй - в котором задано единичное перемещение.
Для рассматриваемого элемента (рис.9.19 и рис.9.20) матрица жесткости элемента имеет следующий вид:
.
Легко увидеть, что каждый столбец этой матрицы состоит из усилий, действующих на узлы элемента при единичном смещении по направлению какой-либо из его степеней свободы при условии, что перемещения по направлению остальных степеней свободы равны нулю.
Например, первый столбец представляет собой усилия, действующие на узлы элемента при единичном смещении узла 1 (4-ый индекс при коэффициентах) по направлению 1 (2-ой индекс при коэффициентах) при условии, что перемещения по направлению остальных степеней свободы равны нулю. Второй столбец представляет собой усилия, действующие на узлы элемента при единичном смещении узла 1 (4-ый индекс при коэффициентах) по направлению 2 (2-ой индекс при коэффициентах) при условии, что перемещения по направлению остальных степеней свободы равны нулю (рис.9.23). И так далее.
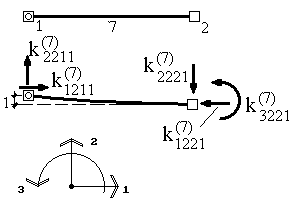
Рис.9.23
Докажем, что это действительно так, например, для первого столбца матрицы жесткости.
Зададим перемещение узла 1 по направлению 1
элемента равным 1, в то время как все его остальные узловые перемещения будем считать
равными нулю. В этом случае вектор узловых перемещений приобретает вид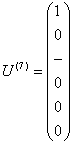 
, и равенство (9.4) становится следующим:
.
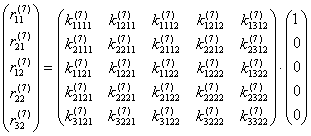Отсюда:
,
т.е. компоненты первого столбца матрицы жесткости на самом деле оказались равными компонентам вектора усилий, действующих на узлы элемента при заданном смещении.
Придавая соответствующий вид вектору узловых перемещений, можно выполнить аналогичное доказательство для любого другого столбца матрицы жесткости элемента.
Для рассматриваемого элемента (рис.9.19) запишем матричное равенство (9.4) в развернутом виде:
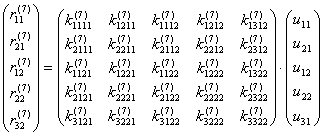
или:
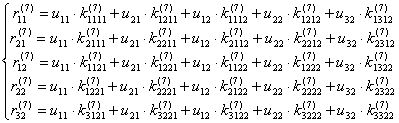
Физический смысл любого из уравнений данной системы очевиден.
Если узел k элемента е получает по направлению j единичное перемещение, то усилие,
действующее при этом на узел m по направлению i равно. Если же это перемещение будет равно не единице, а , то в соответствии с линейным законом связи между усилиями и
перемещениями, рассматриваемое усилие увеличится также в раз и составит 
.
Пусть теперь все узлы элемента получают смещения
по направлению всех имеющихся у элемента степеней свобод. Тогда, в соответствии
с принципом суперпозиций, усилие 
, т.е. усилие, действующее на какой- либо узел m по какому-либо
направлению i,
будет представлять собой сумму усилий, вызванных смещениями всех узлов элемента
по направлению всех имеющихся степеней свобод (рис.9.24). Поскольку, как мы
только что выяснили, при перемещении какого-либо узла k по направлению j на величину на узел m по направлению i будет
действовать усилие , суммарное усилие, действующее на узел m по направлению j, будет
представлять собой сумму величин для всех степеней
свободы элемента (рис.9.24).
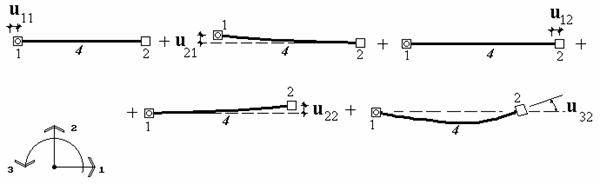
Рис.9.24
Формально это можно записать следующим образом:
,
(9.5)
где
t- номер
узла, входящего в элемент е, запись 
означает, что суммирование
производится по всем узлам, входящим в элемент е, nt
- число степеней свободы в узле t. Причем, nt=2,
если узел t
- шарнирный, и nt=3, если
узел t
жесткий.
Как мы уже выяснили, элементы, стоящие на
главной диагонали матрицы жесткости элемента должны быть положительными. Кроме
того, матрица жесткости элемента должна быть симметричной. Действительно, в
соответствии с теоремой взаимности реакций, усилие, действующее на узел m по направлению i, от единичного
перемещения узла k
этого же элемента по направлению j должно
равняться усилию, действующему на узел k по направлению j, от единичного перемещения узла m этого же элемента по
направлению i,
т.е. 
.
Аналогично векторам и матрица жесткости
элемента также является
блочной. Она состоит из блоков 
, каждый из которых содержит коэффициенты, связывающие
перемещения k-го узла элемента и
реакции, возникающие при этом, в m-ом узле данного элемента.
Например, для рассматриваемого элемента (рис.9.19):
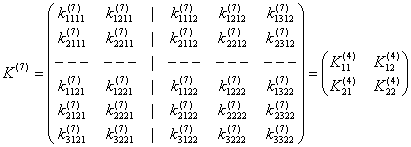
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
