Главная
9.5.6.
Преобразование матрицы жесткости при переходе от одной
системы
координат к другой
Обычно матрицу жесткости строят в удобной для данного элемента системе координат, которую принято называть локальной или местной. При переходе от отдельных элементов к системе элементов необходимо осуществить переход от локальных систем координат к общей для всех элементов системе координат, которую принято называть глобальной.
Пусть известны перемещения какого-либо жесткого узла k элемента в локальной системе координат, оси которой 1` и 2` повернуты на угол j относительно осей 1 и 2 глобальной системы координат. Оси 3 и 3`, очевидно, будут совпадать, т.к. в обоих случаях рассматривается одна и та же плоскость (рис.9.25).
Пусть 
и 
- перемещения узла k по направлению 1 в глобальной и локальной системах
координат соответственно, а 
и 
- перемещения по направлению 2 в глобальной и локальной системах
координат соответственно.
Из рис.9.25 следует:
,
.
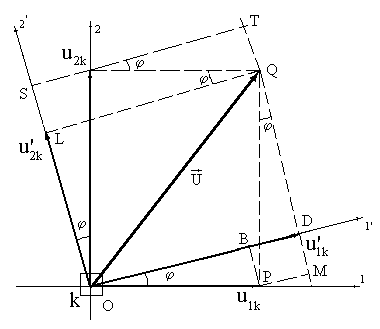
Рис.9.25
Очевидно, угловое смещение в обоих системах осей координат будет одинаковым, т.е. 
. Полученные соотношения, связывающие перемещения узла в
локальной и в глобальной системах координат, в матричной форме будут выглядеть
следующим образом:
.
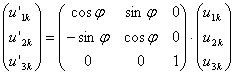Матрица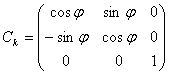 
называется матрицей
направляющих косинусов для k-го узла.
Легко убедиться, что элемент, стоящий в ее i-ой
строке и j-ом
столбце равен косинусу угла между i-ой
осью в локальной системе координат и j-ой
осью в глобальной системе координат.
Для шарнирного элемента связь между перемещениями в локальной и глобальной системах осей будет аналогичной:
.
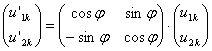Для элемента, содержащего несколько узлов, связь между вектором узловых перемещений U в глобальной системе осей координат и вектором узловых перемещений U` в локальной системе осей координат осуществляется при помощи квазидиагональной матрицы направляющих косинусов C(e) элемента, составленной из матриц направляющих косинусов входящих в элемент узлов:
.
(9.6)
Например, для элемента, изображенного на рис.9.19, выражение (9.6) будет выглядеть следующим образом:
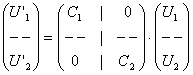
или
.
Легко убедиться, что это равенство соответствует уравнениям, связывающим перемещения в локальной и глобальной системах осей координат:
,
,
,
,
.
Повторив те же рассуждения для усилий,
действующих на узлы элемента, получим аналогичную (9.6) зависимость между
векторами усилий, действующих на элемент, построенных для глобальной системы
координат 
и для локальной
системы координат 
:
.
(9.7)
Усилия, действующие на узлы элемента и узловые перемещения связаны зависимостью (9.3). Запишем ее также и для локальной системы осей координат:
.
(9.8)
Заменим в (9.8) вектора усилий и перемещений согласно зависимостям (9.6) и (9.7):
и умножим получившееся равенство слева на матрицу 
, т.е. на матрицу, обратную матрице направляющих косинусов
элемента: 
. Сопоставляя это выражение с (9.3),
получим зависимость, связывающую матрицы жесткости, построенные в глобальной и
локальной системах координатных осей: 
. Известно, что
у матрицы направляющих косинусов 
обратная матрица
совпадает с транспонированной матрицей. Поэтому, окончательно получаем:
.
(9.9)
Итак, если матрица жесткости элемента построена в локальной системе осей координат, то по формуле (9.9) можно получить из нее матрицу жесткости элемента в глобальной системе осей координат.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
