Главная
9.5.7.
Примеры построения матрицы жесткости конечного элемента
Построим матрицу жесткости элемента на рис.9.26. Пусть L - длина элемента, EF - жесткость стержня на растяжение-сжатие, EI - жесткость стержня на изгиб.
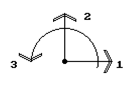
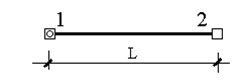
Рис.9.26
Рассматриваемый элемент имеет 5 степеней свободы - две степени свободы в узле 1 и три в узле 2. Соответственно, матрица жесткости элемента имеет размер 5´5 и блочную структуру:
.
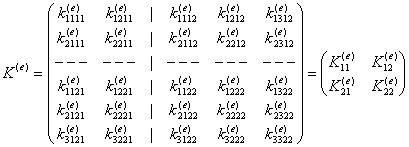Как известно, каждый столбец матрицы жесткости элемента представляет собой усилия, действующие на элемент в узлах при единичном смещении по направлению какой-либо степени свободы. Поэтому, для построения любого столбца матрицы жесткости элемента следует задать единичное смещение по направлению соответствующей степени свободы элемента и найти усилия, действующие при этом на его узлы. Выполнив последовательно эту операцию для всех степеней свободы элемента, по столбцам построим всю матрицу жесткости элемента.
Закрепим от смещения все узлы рассматриваемого элемента (рис.9.27). Тогда, задавая единичное смещение в одной из опорных связей, наложенных на полученную систему, мы обеспечим отсутствие перемещений по направлению остальных связей. Реакции в опорах при этом будут представлять собой искомые усилия.
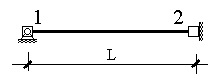
Рис.9.27
Первый столбец матрицы жесткости
рассматриваемого элемента представляет собой усилия в узлах элемента при
единичном смещении узла 1 по направлению 1. При этом на элемент со стороны опорных связей будут
действовать только усилия по направлению 1 (рис.9.28), вызывающие его
сжатие, причем усилие в узле 1 совпадает
по направлению с осью 1, а в узле 2 оно направлено в обратную сторону. Величина
этого усилия будет равна 
. Действительно, продольное усилие N, возникающее в стержне при его растяжении или сжатии, связано с
продольной деформацией (относительным удлинением) 
посредством закона
Гука:
. При 
отсюда имеем
. Таким образом, с учетом знака
элементы первого столбца матрицы жесткости элемента будут равны:
;
;
;
;
.
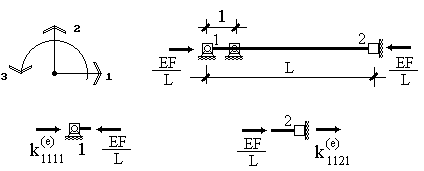
Рис.9.28
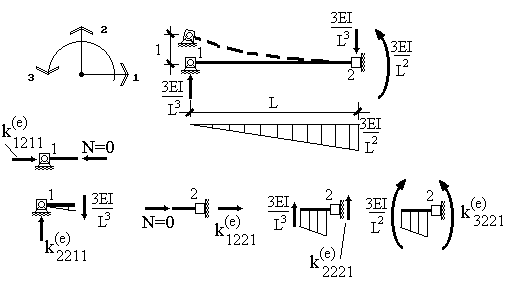
Рис.9.29
Для построения второго столбца зададим единичное смещение в узле 1 по направлению 2 (рис.9.29). Для данной задачи существует известное табличное решение, на основании которого путем рассмотрения равновесия вырезанных из элемента узлов (рис.9.29) определяются элементы второго столбца матрицы жесткости элемента:
;
;
;
;
.
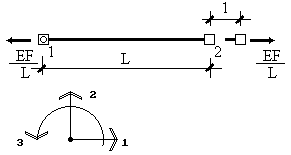
Рис.9.30
Теперь зададим единичное смещение узла 2 по направлению 1 (рис.9.30) и построим третий столбец матрицы жесткости элемента. В этом состоянии элемент будет испытывать продольное растяжение. Повторяя рассуждения аналогичные сделанным при построении первого столбца матрицы жесткости, получим:
;
;
;
;
.
Рис.9.31
Для построения четвертого столбца матрицы жесткости зададим единичное смещение узла 2 по направлению 2 (рис.9.31):
;
;
;
;
.
И наконец, для
построения пятого столбца матрицы жесткости зададим единичное смещение узла 2
по направлению 3 (рис.9.32):
;
;
;
;
.
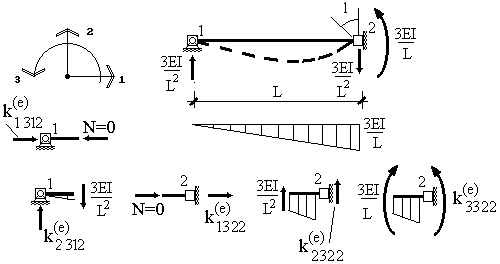
Рис.9.32
Итак, матрица жесткости рассматриваемого элемента принимает вид:
.
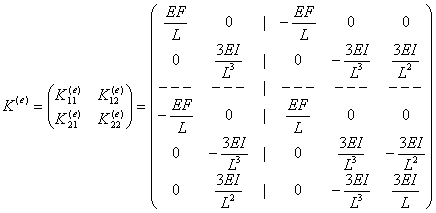Как и следовало ожидать, построенная матрица оказалась симметричной, а элементы, стоящие на ее главной диагонали, оказались положительными. Проверка выполнения этих условий - одно из средств контроля правильности построения матрицы жесткости.
Рассмотрим теперь Г-образный элемент (рис.9.33). Будем считать, что жесткости обоих стержней элемента равны. Ограничимся построением для него только пятого столбца матрицы жесткости, предоставив построение остальных столбцов читателю.
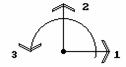
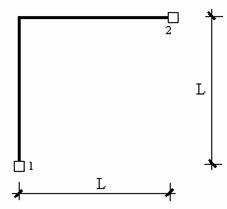
Рис.9.33
В данном элементе два жестких узла, следовательно, элемент имеет шесть степеней свободы, а матрица жесткости элемента имеет следующую блочную структуру:
.
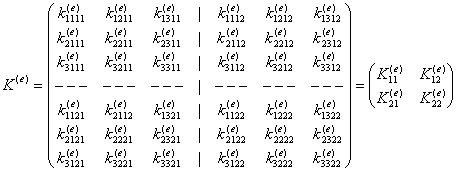Элементы интересующего нас пятого столбца матрицы жесткости представляют собой усилия, действующие на узлы элемента при единичном смещении узла 2 по направлению 2. Для их определения нужно найти опорные реакции в стержневой системе, полученной при наложении связей по направлению всех степеней свободы элемента (рис.9.34), при единичном смещении ее верхней опоры по направлению 2.
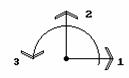
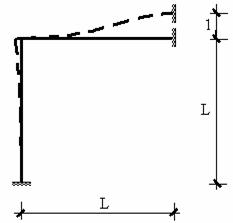
Рис.9.34
Данная задача три раза статически неопределима nст=6+3∙0-3-0=3 и один раз кинематически неопределима nкин=1+0, следовательно, для ее решения выгоднее использовать метод перемещений. При этом, как обычно в методе перемещений, будем пренебрегать продольными деформациями стержней по сравнению с их изгибными деформациями.
Основную систему метода перемещений образуем введением в жесткий узел связи, препятствующей его повороту. Потребовав, чтобы при повороте этого узла на величину Z реакция R во введенной связи равнялась нулю, получим задачу эквивалентную исходной (рис.9.35).
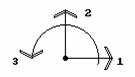
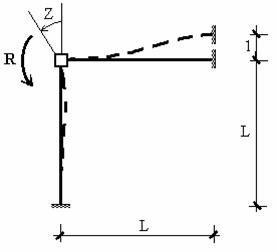
Рис.9.35
Далее построим основное и вспомогательное
состояния основной системы (рис.9.36). Из равновесия узла (рис.9.36) находим
реакции во введенной связи в основном и вспомогательном состояниях:
, 
. Из уравнения, выражающего условие отсутствия реакции во
введенной связи в эквивалентной задаче 
, находим: 
.
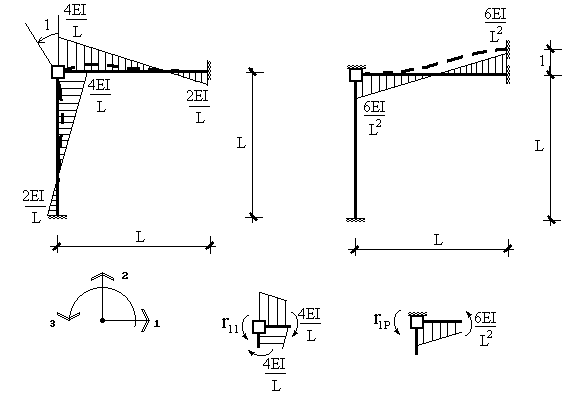
Рис.9.36
Найдя лишнее неизвестное, можем построить окончательную
эпюру моментов (рис.9.37), пользуясь формулой 
. По построенной эпюре моментов путем вырезания узлов легко
определить действующие в стержнях продольные и поперечные силы, а по ним и
реакции в опорах (рис.9.37). Таким образом, по реакциям в опорах определяются элементы искомого столбца
матрицы жесткости:
;
;
;
;
;
.
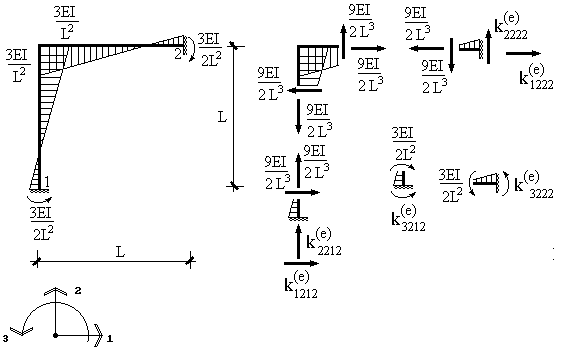
Рис.9.37
Важно иметь в виду, что продольные деформации в стержнях при определении этих значений не учитывались, поэтому использование построенной подобным образом матрицы жесткости элемента в расчетах будет приводить к погрешностям в решении. В элементах, представляющих собой один стержень (рис.9.6), учет продольных деформаций проблем не вызывает. Поэтому использование в конечно-элементной схеме только таких элементов позволит получить точное решение задачи, если не учитывать погрешностей округления.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
