Главная
9.5.8.
Формирование и решение системы уравнений МКЭ.
Определение
внутренних усилий в элементах
Обозначим ![]() -внешнее усилие, приложенное к узлу m и действующее
по направлению i.
Введем для каждого из n
узлов конечно-элементной схемы вектор внешних узловых усилий, приложенных к
узлу m.
Если узел m
- жесткий, то
-внешнее усилие, приложенное к узлу m и действующее
по направлению i.
Введем для каждого из n
узлов конечно-элементной схемы вектор внешних узловых усилий, приложенных к
узлу m.
Если узел m
- жесткий, то 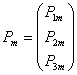 , если шарнирный, то
, если шарнирный, то 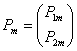 .
.
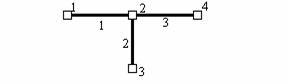
Рассмотрим равновесие любого свободного узла (т.е. такого узла, на перемещения которого не наложены связи) конечно-элементной сетки. Пусть это будет узел под номером 2 конечно-элементной сетки, изображенной на рис.9.38. Будем считать пока, что все узлы этой сетки свободны, т.е. на узлы не наложено связей. Об учете связей речь пойдет далее.
На
узел действует внешняя узловая нагрузка, характеризующаяся вектором 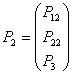 , передаваемая на элементы, которые соединяются в этом узле.
Пусть это будут три элемента под номерами 1, 2 и 3 (рис.9.38).
, передаваемая на элементы, которые соединяются в этом узле.
Пусть это будут три элемента под номерами 1, 2 и 3 (рис.9.38).
![]()
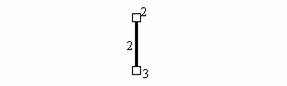
Рис.9.38
Усилия, передаваемые на элемент е
в узле 2, в соответствии с введенным ранее
обозначением образуют вектор ![]() . Соответственно, со
стороны элементов на узел передаются равные, но противоположно направленные
усилия. Т.е. со стороны элемента е на узел действует система усилий, образующих вектор -
. Соответственно, со
стороны элементов на узел передаются равные, но противоположно направленные
усилия. Т.е. со стороны элемента е на узел действует система усилий, образующих вектор -![]() . Узел элемента должен находиться в равновесии под действием
внешних усилий и усилий, приложенных к узлу со стороны элементов.
Следовательно, можно записать:
. Узел элемента должен находиться в равновесии под действием
внешних усилий и усилий, приложенных к узлу со стороны элементов.
Следовательно, можно записать:
![]() .
(9.10)
.
(9.10)
Следует помнить, что данное равенство - матричное равенство и соответствует системе равенств, каждое из которых представляет собой уравнение равновесия усилий, действующих на узел по одному из направлений. Так как узел 2 - жесткий, это равенство принимает следующий вид (рис.9.39):
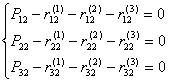 .
.
В дальнейшем, для упрощения выкладок будем пользоваться матричной формой записи, не раскладывая равенства покомпонентно.
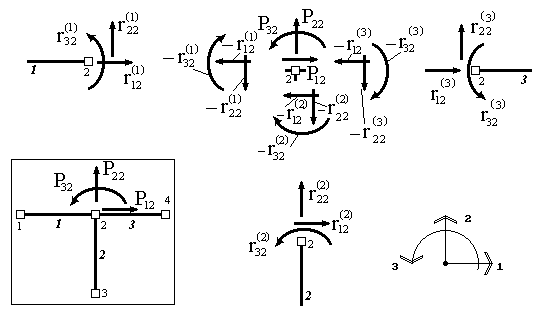
Рис.9.39
В соответствии с (9.4) для элемента 1
справедливо соотношение ![]() или
или 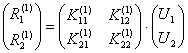 . Из него вектор усилий, действующих на узел 2 со стороны
элемента 1, окажется равным
. Из него вектор усилий, действующих на узел 2 со стороны
элемента 1, окажется равным ![]() .
.
Аналогично, для элемента 2 будем иметь: ![]() или
или 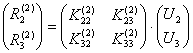 . Из него вектор усилий, действующих на
узел 2 со стороны элемента 2 окажется равным
. Из него вектор усилий, действующих на
узел 2 со стороны элемента 2 окажется равным ![]() .
.
Аналогично,
для элемента 3 будем иметь: ![]() или
или 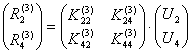 . Из него вектор усилий, действующих на
узел 2 со стороны элемента 3 окажется равным
. Из него вектор усилий, действующих на
узел 2 со стороны элемента 3 окажется равным ![]() .
.
Подставив полученные выражения в (9.8), получим:
![]() ,
,
откуда:
![]() .
.
Отсюда видно, что в уравнение равновесия для узла входят компоненты матриц жесткости только тех элементов, которые примыкают к этому узлу. Кроме того, в это уравнение входят перемещения только тех узлов, которые принадлежат элементам, примыкающим к рассматриваемому узлу.
Повторив аналогичные операции для всех узлов конечно-элементной схемы, изображенной на рис.9.38, получим:
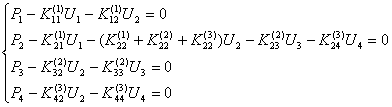 .
.
Запишем эту систему в матричной форме:
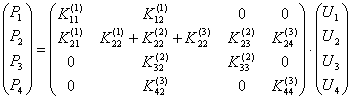 .
(9.11)
.
(9.11)
Введем вектор перемещений узлов конечно-элементной
сетки U, компонентами которого
являются перемещения по направлению всех степеней свободы системы. Очевидно,
этот вектор состоит из блоков - векторов перемещений ![]() всех n узлов системы:
всех n узлов системы:
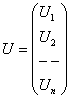 .
.
Аналогично, введем вектор внешних узловых усилий P, действующих на конечно-элементную схему. Этот вектор также будет состоять из блоков - векторов усилий Рi, действующих на каждый узел системы:
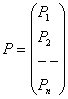 .
.
Тогда полученная выше система уравнений (9.11) может быть записана в виде:
![]() .
(9.12)
.
(9.12)
Зависимость (9.12) устанавливает связь между перемещениями узлов конечно-элементной сетки и приложенными к ним узловыми воздействиями. Зависимость (9.12) аналогична зависимости (9.4), но она построена не для отдельного элемента, а для всей конечно-элементной схемы. Матрица К, как и матрица жесткости элемента, связывает перемещения узлов и приложенные к ним воздействия, но не для одного элемента, а сразу для всей системы. Поэтому ее называют матрицей жесткости конечно-элементной схемы или глобальной матрицей жесткости.
Глобальная матрица жесткости - квадратная матрица, размером равным числу степеней свободы системы, имеющая, как видно из (9.11) блочную структуру.
Из (9.11) легко заключить, что блок ![]() глобальной матрицы
жесткости формируется из блоков
глобальной матрицы
жесткости формируется из блоков ![]() матриц жесткости
элементов е, входящих в
конечно-элементную схему, причем представляет собой сумму блоков
матриц жесткости
элементов е, входящих в
конечно-элементную схему, причем представляет собой сумму блоков ![]() для тех элементов конечно-элементной схемы, в состав которых
входит узел i:
для тех элементов конечно-элементной схемы, в состав которых
входит узел i:
![]() ,
(9.13)
,
(9.13)
где
запись ![]() означает, что элемент е должен принадлежать множеству
элементов, в состав которых входит узел i.
означает, что элемент е должен принадлежать множеству
элементов, в состав которых входит узел i.
Действительно, в рассмотренном примере
(рис.9.38) узел 2 входит в состав трех элементов 1, 2 и 3, значит
блок ![]() формируется из
соответствующих блоков матриц жесткости этих трех элементов путем их прямого
суммирования. Но ни один элемент не соединяет, например, узлов 1 и 3, следовательно блок
формируется из
соответствующих блоков матриц жесткости этих трех элементов путем их прямого
суммирования. Но ни один элемент не соединяет, например, узлов 1 и 3, следовательно блок ![]() глобальной матрицы
жесткости представляет собой нулевую матрицу.
глобальной матрицы
жесткости представляет собой нулевую матрицу.
В системе (9.12) вектор внешних сил Р задается, глобальная матрица жесткости К, как мы только что выяснили, формируется из матриц жесткости элементов, входящих в конечно-элементную сетку. Неизвестными в этой системе являются перемещения узлов сетки, составляющие компоненты вектора U.
Таким образом, после построения вектора внешних нагрузок и формирования глобальной матрицы жесткости конечно-элементной схемы перемещения ее узлов определяются посредством решения системы линейных алгебраических уравнений МКЭ (9.12).
Легко показать, что в силу симметрии матриц жесткости элементов и в соответствии с (9.13) глобальная матрица жесткости также будет симметричной.
Если на перемещения какого-либо из узлов конечно-элементной схемы наложены ограничения (рис.9.40), то уравнения равновесия для этого узла теряют смысл. Действительно, все приложенные к этому узлу силы, как внешняя нагрузка, так и усилия, действующие со стороны стержней, будут восприниматься опорными связями. Зато, заранее известны перемещения по направлениям закрепленных степеней свободы такого узла. Поэтому, в системе уравнений (9.12) для тех степеней свободы, на которые наложены ограничения, соответствующие уравнения равновесия заменяются уравнениями, в которых перемещениям присваиваются заданные значения.
На практике глобальная матрица жесткости строится в соответствии с вышеописанной процедурой, без учета ограничений на перемещения, что и было проделано выше. И только после этого, в матрицу и систему уравнений (9.12) вносятся изменения, позволяющие учесть наличие связей.
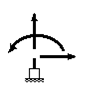
Рис.9.40
Рассмотрим в качестве примера систему, изображенную на рис.9.6. Очевидно, она имеет 8 степеней свободы.
Предположим, что нам удалось построить матрицы
жесткости всех входящих в нее элементов и в соответствии с (9.13) сформировать
из них глобальную матрицу жесткости и систему линейных алгебраических уравнений
![]() или
или
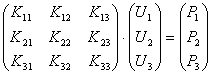 .
.
Поскольку узел 1 закреплен от смещений, все
три его перемещения равны нулю.
Следовательно, уравнения равновесия первого узла в данной системе (они
выражаются матричным равенством ![]() ) должны быть заменены условиями равенства нулю перемещений
по направлению всех степеней свободы
узла 1. Эти условия характеризуются матричным равенством
) должны быть заменены условиями равенства нулю перемещений
по направлению всех степеней свободы
узла 1. Эти условия характеризуются матричным равенством ![]() . В результате система разрешающих уравнений МКЭ приобретет
вид:
. В результате система разрешающих уравнений МКЭ приобретет
вид:
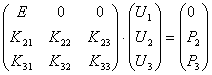 ,
,
где Е - единичная матрица.
При перемножении матриц блоки ![]() и
и ![]() должны быть умножены
на блок
должны быть умножены
на блок ![]() , о котором заранее известно, что он является нулевым.
Поэтому над данной системой можно выполнить еще одно преобразование:
, о котором заранее известно, что он является нулевым.
Поэтому над данной системой можно выполнить еще одно преобразование:
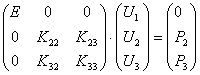 .
.
Подобная замена не изменит решение системы уравнений, но сделает матрицу симметричной, что выгодно с точки зрения ее хранения в памяти компьютера и решения системы.
В развернутой форме полученная система будет иметь вид:
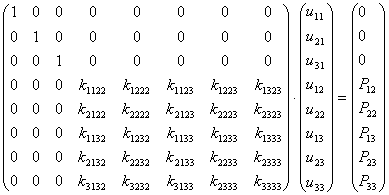 .
.
Таким образом, если перемещение по направлению одной из степеней свободы заранее задано равным нулю, все элементы матрицы системы разрешающих уравнений метода конечных элементов в соответствующей данному перемещению строке и столбце с тем же номером задаются равными нулю, за исключением элемента, стоящего на главной диагонали, который задается равным единице. Кроме того, элемент, стоящий в этой строке в векторе свободных членов также задается равным нулю.
В случае, если
заданные смещения в узле оказываются равными ненулевым величинам, например, для
рассматриваемого случая ![]() ,
, ![]() ,
, ![]() система уравнений
метода конечных элементов приобретет следующий вид:
система уравнений
метода конечных элементов приобретет следующий вид:
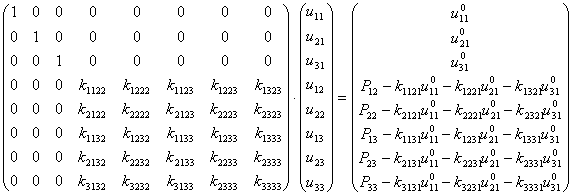 .
.
В результате решения системы уравнений МКЭ
определяются все перемещения узлов конечно-элементной схемы. А значит, в
формуле (9.4) для каждого элемента системы становятся известными вектора ![]() . Зная их и матрицы жесткости элементов по
этой формуле легко определяются усилия, действующие на каждый элемент со
стороны узлов (т.е. вектора
. Зная их и матрицы жесткости элементов по
этой формуле легко определяются усилия, действующие на каждый элемент со
стороны узлов (т.е. вектора ![]() ). Зная их значения, построить эпюры внутренних усилий на
элементах не составит труда.
). Зная их значения, построить эпюры внутренних усилий на
элементах не составит труда.
При необходимости определить усилия,
действующие на элементы, в локальных системах координат, для каждого элемента
следует по формуле (9.6) осуществить переход от найденных векторов ![]() к векторам
к векторам ![]() , и затем, найти искомые усилия (т.е. вектора
, и затем, найти искомые усилия (т.е. вектора ![]() ) по формуле (9.8).
) по формуле (9.8).
На этом расчет системы на узловые воздействия заканчивается. Для получения окончательных значений внутренних усилий в стержнях системы, как уже упоминалось, необходимо сложить полученные от узловых воздействий внутренние усилия с усилиями, определенными при условии закрепления всех узлов (сложить решения задачи 1 и задачи 2).
При решении задачи методом конечных элементов на ЭВМ после задания исходных данных, а именно геометрии стержневой системы, жесткостных характеристик стержней, нагрузок и закреплений, от человека не требуется вмешательства для выполнения каких-либо промежуточных операций, например, создания основной системы или построения вспомогательных состояний. ЭВМ способна автоматически выполнить все вышеописанные процедуры: построение матриц жесткости элементов на основании хранящихся в памяти формул для библиотечных элементов, формирование глобальной матрицы жесткости, решение системы, определение усилий в стержнях элементов.
Алгоритм метода универсален, т.е. не зависит от того, является ли рассматриваемая система статически или кинематически определимой или неопределимой, а также от степени ее статической или кинематической неопределимости. Более того, МКЭ позволяет рассчитывать системы, состоящие не только из стержневых элементов, но и пластинчатых, оболочечных, трехмерных, разнообразных элементов на винклеровском основании и других элементов, матрицы жесткости которых учитываются в глобальной матрице жесткости системы также, как и матрицы жесткости стержневых элементов. Это, в частности, позволяет сразу подвергать расчету весь комплекс “сооружение-фундамент-основание”.
Современные программные комплексы, как правило, содержат мощные графические средства, позволяющие быстро и легко задать все исходные данные для расчета (препроцессор), а также просмотреть и проанализировать полученные результаты, выполнить подбор сечений стержней или арматуры в соответствии с нормативной документацией (постпроцессор). То есть работа с такими программными продуктами практически осуществляется по принципу “нажми на кнопку - получишь результат”. Тем не менее, при всей развитости и разнообразии препроцессорных и постпроцессорных средств в подобных программных комплексах, в основе их ядра (процессора) лежит программная реализация одного и того же алгоритма - алгоритма метода конечных элементов
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21