Главная

58. Расчет статически неопределимых арок

Арки могут быть трехшарнирными – статически определимые (рассмотрели ранее); двухшарнирные – один раз статически неопределимы; одношарнирными – дважды статически неопределимы и бесшарнирные. К бесшарнирной арке можно свести задачу о своде – пространственной распорной системе. Для перехода от свода к арке следует вырезать из свода (мысленно, естественно) полосу двумя параллельными плоскостями, отстоящими друг от друга на расстоянии единица.

В мостовых конструкциях чаще применяются двух- и бесшарнирные арки.

58.1. Двухшарнирные арки

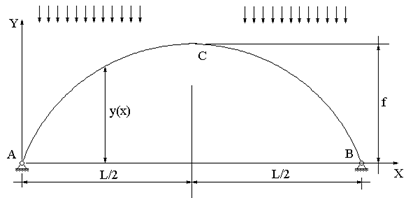
Рис. 58.1

Двухшарнирная арка представляет собой шарнирно опертый криволинейный стержень, причем обе его опоры являются неподвижными (рис.58.1).

Такая арка является один раз статически неопределимой. Действительно, в ее опорах возникают четыре реакции - две вертикальных и две горизонтальных, а уравнений равновесия для арки можно составить только три.

Как показал опыт расчета, наибольшие внутренние усилия и напряжения возникают в середине пролета арок такого типа. Поэтому двухшарнирные арки часто конструируют таким образом, чтобы жесткость в центре пролета была выше, чем на опорах (рис. 58.2).

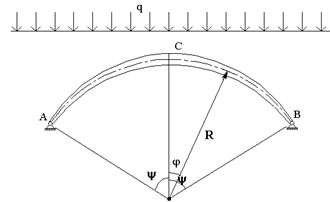
Рис. 58.2

Например, для арок кругового очертания закон изменения момента инерции сечения по длине криволинейного стержня можно задать следующим:

где - момент инерции сечения на оси симметрии арки, n - некоторый положительный параметр. Очевидно, при n=0 жесткость арки оказывается постоянной по ее длине.

Здесь значения угла меняются от до и являются отрицательными на левой половине арки и положительными на правой. Расчет двухшарнирных арок будем выполнять методом сил. Основную систему образуем отбрасыванием горизонтальной связи на одной из опор и заменой ее действия неизвестным усилием (рис.58.3).

Задачу, эквивалентную исходной, получим из основной системы, поставив дополнительное условие - отсутствие перемещений по направлению отброшенной связи . Неизвестное усилие найдем из канонического уравнения метода сил:

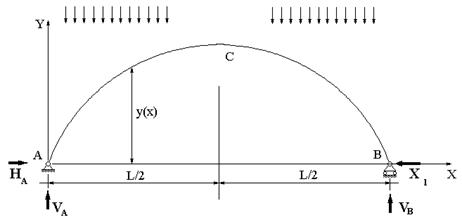
Рис. 58.3

коэффициенты которого определяются по формулам Максвелла-Мора:

Здесь интегралы берутся по длине L криволинейного стержня арки, а остальные обозначения - стандартные, принятые в методе сил.

Таким образом, при расчете двухшарнирной арки используется алгоритм классического метода сил для один раз статически неопределимой стержневой системы, т.е. определяются законы изменения изгибающих моментов в основной системе для грузового и вспомогательного состояний и соответственно, по формулам (58.3) и (58.4) вычисляются коэффициенты разрешающего уравнения метода сил (58.2), решением которого является неизвестное усилие в одной из опор.

Окончательные эпюры моментов в арке строятся по формуле:

Остальные реакции в опорных связях находятся из уравнений равновесия.

Так, составив условие равенства нулю суммы проекций всех сил на горизонтальную ось, получим:

где - сумма проекций внешних сил на горизонтальную ось х. Если горизонтальная составляющая нагрузки отсутствует, то горизонтальные реакции в обеих опорах оказываются равными, а сами эти реакции, как известно, представляют собой возникающий в системе распор.

Вертикальные реакции определяются из условия равенства нулю суммы проекций всех сил на вертикальную ось y и суммы моментов всех сил относительно точки А:

где - сумма проекций всех внешних сил на вертикальную ось, а - сумма моментов всех внешних сил относительно точки А.

После того, как определены опорные реакции, перерезывающие и продольные усилия в арке находятся точно также, как в статически определимой трехшарнирной арке по формулам:

где угол наклона касательной к оси арки в данной точке (рис. 58.4). Для арок кругового очертания .

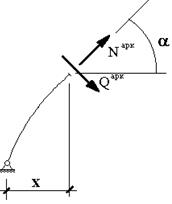
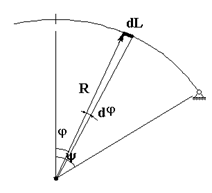
Рис. 58.4 Рис. 58.5

Наибольшие сложности при выполнении расчета возникают при вычислении криволинейных интегралов в (58.3) и (58.4). В случае арки кругового очертания длина бесконечно малого участка арки dL связана с бесконечно малым приращением угла зависимостью (рис. 58.5).

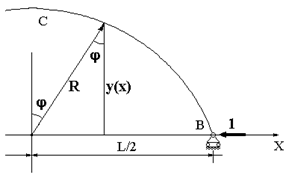
Рис. 58.6

Рассмотрим вспомогательное состояние основной системы (рис. 58.6). Легко убедиться, что вертикальные реакции в опорах арки будут отсутствовать, а изгибающий момент в сечениях арки определяется по формуле . Таким образом, выражения (58.3) и (58.4) приобретают вид:

Интегралы (58.11) и (58.12) могут быть вычислены различными способами. В случае арки постоянной жесткости и достаточно простой нагрузки (т.е. при простом виде функции ) может быть использовано аналитическое вычисление интегралов. В более сложных случаях - численное интегрирование, например при помощи математических пакетов типа MathCad.

В качестве примера рассмотрим расчет полукруглой арки постоянной по длине жесткости, изображенной на рис. 58.7.

В грузовом состоянии в опорах арки возникают вертикальные реакции величиной P/2 каждая (рис. 58.8).

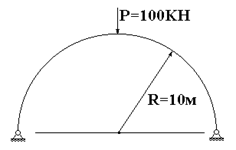
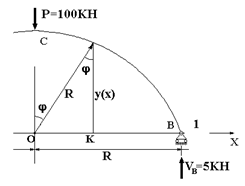
Рис. 58.7 Рис. 58.8

В результате, изгибающий момент на правой половине арки составит:

На левой половине арке с учетом того, что угол φ отрицательный, изгибающий момент окажется равным

После подстановки этого выражения в (58.11) и (58.12), с учетом того, что , получим: и

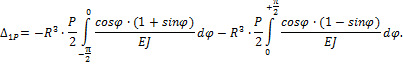
Т.к. жесткость арки постоянна, внутренние усилия в ней не зависят от величины EJ. Задав EJ=1 с помощью пакета MathCad получим: и

Отсюда следует: и , и, в соответствии с (58.3), величина распора составит кН.

Далее, в соответствии с (58.5) получим выражение для изгибающего момента на правой половине арки:

и на левой половине арки:

Зная теперь все реакции в опорах арки (горизонтальный распор кН, вертикальная реакция кН), найдем продольное и перерезывающее усилия по формулам (58.9) и (58.10) (рис. 58.9).

Напомним, что при выводе формул (58.9) и (58.10) положительными направлениями и считаются такие направления, при которых соответствующие им внутренние усилия будут положительными.

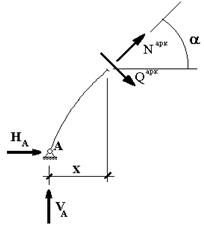
Рис. 58.9

Результаты расчетов для левой половины арки приведены в таблице 58.1. Решение на правой половине арки можно построить, исходя из симметрии задачи.

Таблица 58.1

Угол , град.	Изгибающий момент	Перерезывающее усилие	Продольное усилие
-90	0	-31,83	-50,00
-75	-65,34	-17,80	-56,53
-60	-92,16	-2,57	-59,21
-45	-78,63	12,85	-57,86
-30	-25,66	27,39	-52,57
-15	+63,1	40,06	-43,69
0	+181,7	50,00	-31,83

Эпюры внутренних усилий для рассматриваемой арки приведены на рис. 58.10 - 58.12.

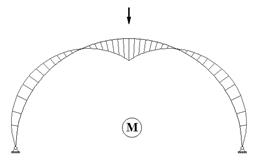
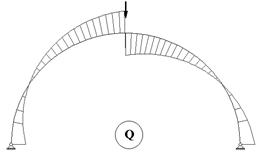
Рис. 58.10 Рис. 58.11

Рис. 58.12

Как и следовало ожидать, на опорах значение перерезывающего усилия равно распору, а продольных усилий - вертикальным реакциям опор. В то же время значение продольного усилия на оси арки равно распору.

Величина максимального изгибающего момента в простой балке на двух опорах, перекрывающей тот же пролет 10 м и находящейся под действием такой же нагрузки (рис.58.13) составит кН∙м, что заметно выше, чем в арке. Как и в трехшарнирной арке, это связано с положительным влиянием арочного распора.

Рис. 58.13

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00