Главная
60.
Кольцевые системы
Кольцевыми системами называют замкнутые системы криволинейных стержней. Расчетные схемы кольцевых систем используются при расчетах трубопроводов, сосудов высокого давления, силосных башен и других подобных систем.
Кольцевая система, изображенная на рис. 60.1,
представляет собой три раза статически неопределимую систему. Действительно,
если рассечь ее в каком-либо сечении, т.е. удалить три связи, получим
статически определимую систему. Действие отброшенных связей заменим тремя
неизвестными 
и 
, построив таким
образом основную систему. Рассмотрим дальнейший расчет этой системы (рис. 60.1).
Зададим P=10 кН, R=1 м. Изгибную жесткость EJ криволинейного стержня будем считать неизменной по длине, что даст возможность задать EJ=1 при расчете внутренних усилий в системе.
Сечение выполним на оси симметрии системы, заменив силу Р системой из двух сил величиной P/2, которые приложены слева и справа от сечения бесконечно близко к нему. Тогда основная система останется симметричной, как и исходная система, и можно будет ограничиться расчетом ее половины (рис. 60.2).
Как известно, на оси симметрии перерезывающая
сила должна равняться нулю, поэтому в задаче остаются только две неизвестные -
продольное усилие 
и
изгибающий момент 
на оси
симметрии. Задача, эквивалентная исходной получится из основной системы путем
постановки условий отсутствия перемещений по направлению отброшенных связей, из
которых следует классическая система разрешающих уравнений метода сил,
коэффициенты которой определяются по формулам Максвелла-Мора.
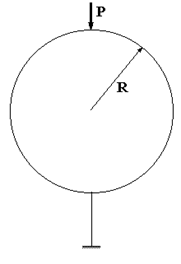
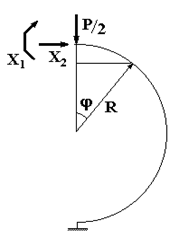
Рис.
60.1
Рис. 60.2
Выражения для изгибающих моментов, очевидно будут иметь следующий вид:
-в первом вспомогательном состоянии: 
;
-во втором вспомогательном состоянии: 
;
-в
грузовом состоянии: 
.
Вычислим далее значения коэффициентов системы разрешающих уравнений метода сил. Воспользовавшись, например, пакетом MathCad, получим:
Система канонических уравнений метода сил имеет вид:
Решением этой системы являются 
кН, 
.
Вообще говоря, вывод о том, что продольное усилие на оси системы нулевое, можно было сделать и раньше из следующих соображений. Со стороны опоры на кольцо действует только вертикальная реакция величиной Р, направленная вверх. В этом легко убедиться или составив уравнения равновесия для системы или исходя из того, что наличие момента и горизонтальной реакции в опоре опять-таки противоречило бы условию симметрии задачи. Следовательно, горизонтальная ось, проходящая через центр окружности, тоже является осью симметрии, а значит перерезывающее усилия в крайней левой и правой точках кольца равны нулю. Из условия равенства нулю суммы проекций всех действующих на систему сил на горизонтальную ось для фрагмента системы, приведенного на рис. 60.3, легко увидеть, что продольное усилие в крайней верхней точке кольца, а значит и в крайней нижней его точке должны равняться нулю.
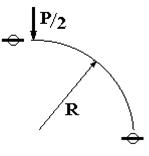
Рис.
60.3
Кстати, сразу же можно сделать вывод о том, что продольное усилие в крайней левой и правой точках системы должны равняться –P/2.
Изгибающий момент в сечениях криволинейного
стержня определяется по формуле 
. Результаты расчета по этой формуле сведены
в таблицу 60.1. В силу наличия в системе двух осей симметрии построить эпюру
изгибающих моментов достаточно для одной четверти кольца. На остальной части
построение производится, исходя из симметрии задачи.
Таблица 60.1
|
Угол град. |
Изгибающий момент, кНм
|
|
0 |
3,1831 |
|
15 |
1,889 |
|
30 |
0,6831 |
|
45 |
-0,35243 |
|
60 |
-1,14703 |
|
75 |
-1,64653 |
|
90 |
-1,8169 |
Формулы для определения в сечениях криволинейного стержня продольного и перерезывающего усилий читателю предлагается получить и проверить (значения этих усилий на осях симметрии уже известны) самостоятельно. Эпюры внутренних усилий приводятся на рис.60.4 – 60.6.
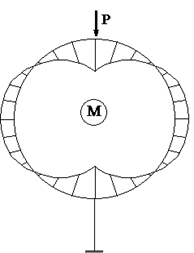
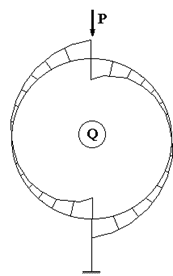
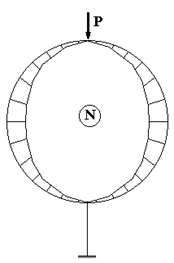
Рис. 60.4
Рис. 60.5 Рис.
60.6
Теперь рассмотрим кольцевую систему радиусом R (рис. 60.7), находящуюся под действием внутренней равномерно распределенной нагрузки q. Подобная ситуация возникает, например, при расчете трубопровода высокого давления, если q - давление находящегося внутри трубопровода газа.
Очевидно, равнодействующая приложенной к системе нагрузки равна нулю, следовательно, реакции опор в системе также будут нулевыми. Значит любая прямая, проходящая через центр окружности, в данной системе будет являться осью ее симметрии. Следовательно, во всех сечениях перерезывающая сила Q будет равна нулю.
Из равенства нулю перерезывающей силы
следует, что изгибающий момент должен быть постоянным 
. Докажем, что он должен быть равен нулю.
Доказательство будем вести от противного. Пусть изгибающий момент во всех
сечениях рассматриваемой системы постоянный и отличный от нуля. Выполним для
данной ситуации деформационную проверку.
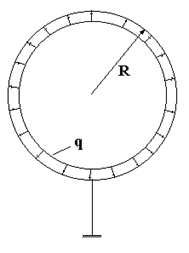
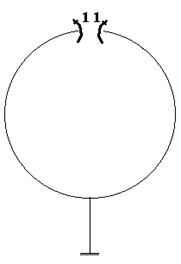
Рис.
60.7
Рис. 60.8
Как известно, если построить любое вспомогательное состояние для любой основной системы, образованной из исходной, то должно выполняться равенство
(60.1)
где L
- длина интегрирования, 
-
окончательный закон изменения изгибающего момента, полученный в результате
расчета, 
-
закон изменения изгибающего момента во вспомогательном состоянии.
Образуем основную систему также,
как в предыдущей задаче, отбросив три связи на вертикальной оси системы
в ее крайней верхней точке. В качестве вспомогательного состояния возьмем,
например, состояние, изображенное на рис. 60.8. В этом состоянии будет =1. Следовательно, равенство (60.1) не может
быть верным, т.к. имеет
один знак по всей длине интегрирования L.
Значит наше предположение, что отличен от нуля неверно.
Итак, мы доказали, что изгибающий момент во всех сечениях рассматриваемой системы отсутствует. Кстати, в этом случае равенство (60.1) выполняется автоматически для любого вспомогательного состояния любой основной системы.
Итак, при действии внутренней равномерно распределенной нагрузки на кольцевые системы единственным ненулевым усилием в них оказывается продольное усилие. Для его определения рассмотрим равновесие, например верхней половины кольца (рис. 60.9). В силу симметрии по вертикальной оси продольные усилия в местах, где выполнены сечения должны быть одинаковыми и равными N.
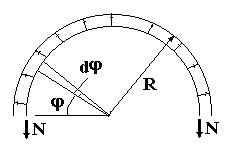
Рис. 60.9
Составим уравнение проекций всех сил на
вертикальную ось. Нагрузка, действующая на бесконечно малый участок
криволинейного стержня длиной 
даст
на вертикальную ось проекцию величиной 
. Интегрируя эту величину по 
от 0
до 
, получим проекцию равнодействующей нагрузки
на вертикальную ось: 
. Из условия равенства нулю суммы проекций
всех действующих на рассматриваемую часть системы сил
на вертикальную ось получим: 
, следовательно:
Аналогичный результат получится, если рассмотреть равновесие любой другой части системы. То есть продольные усилия в данной задаче являются растягивающими, одинаковы по всей длине криволинейного стержня и определяются по формуле (60.2). Эта формула известна в инженерном деле как котельная формула.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
