Главная

11.2. Построение линий влияния опорных моментов
кинематическим методом

Для построения линии влияния какого-либо усилия кинематическим методом необходимо в сооружении нарушить ту связь, которая передает это усилие, и заменить нарушенную связь усилием . В полученной основной системе перемещение по направлению нарушенной связи от действия подвижной одиночной силы и усилия должно равняться нулю:

, (11.7)

откуда .

Учитывая, что на основании теоремы о взаимности перемещений , окончательно получим:

, (11.8)

где - перемещение по направлению подвижной единичной нагрузки от усилия S_i = 1.

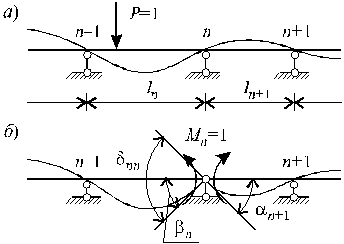
Рис.11.3

Например, если необходимо определить линию влияния опорного момента в n-ом опорном сечении многопролетной балки, расчетная схема заданной и основной системы принимает вид, показанный на рис.11.3.

Если подвижная единичная сила занимает произвольное положение, то представляет собой эпюру перемещений (упругую линию) основной системы от усилия = 1.

Перемещение от усилия = 1 по направлению этого же усилия является величиной постоянной и называется масштабом эпюры перемещений.

Изобразив примерный вид упругой линии основной системы от усилия , получим очертание линии влияния усилия , так называемую модель линии влияния . Таким образом, кинематический метод дает возможность быстро получить внешний вид (модель) любой линии влияния.

Для построения линии влияния усилия необходимо вычислить ординаты упругой линии основной системы от усилия и поделить их на постоянную величину (-).

Рассмотрим примеры построения линий влияния усилий в неразрезной балке кинематическим методом. Применим кинематический метод к построению линии влияния опорного момента М₂ неразрезной балки (рис.11.4, а).

Для получения основной системы в сечение балки над опорой 2 введем шарнир и заменим нарушенную связь парными моментами М₂ = 1 (рис.11.4, в). Уравнение совместности деформаций имеет вид , из которого следует, что

. (11.9)

В основной системе каждый пролет можно представить как балку на двух шарнирных опорах, нагруженную одним или двумя опорными моментами. 

Уравнения прогибов и углов поворота для балки на двух опорах с одним опорным моментом М = 1 (см. рис.11.5) можно легко рассчитать методом начальных параметров. Вводя обозначение , получим:

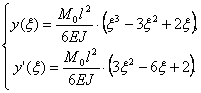(11.10)

Для облегчения подсчета ординат эпюры прогибов М_P2 на рис.11.5 показана упругая линия балки на двух шарнирных опорах, нагруженной одним опорным моментом М = 1, и указаны углы поворота на опорах и прогибы через 0,2l.

Как видно из рис.11.4, б, (n = 2) перемещение представляет собой взаимный угол поворота двух смежных сечений основной системы на опоре n = 2. Этот угол можно подсчитать также, используя упругую линию балки на двух опорах, показанную на рис.11.5. 

Запишем систему уравнений трех моментов (исключая для опоры 2) для определения изгибающих моментов на опорах от действия М₂ = 1:

(11.11)

Учитывая, что М₀ = М₅ = 0, а также, что M₂ = 1, получаем: 

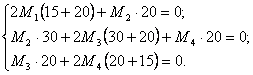
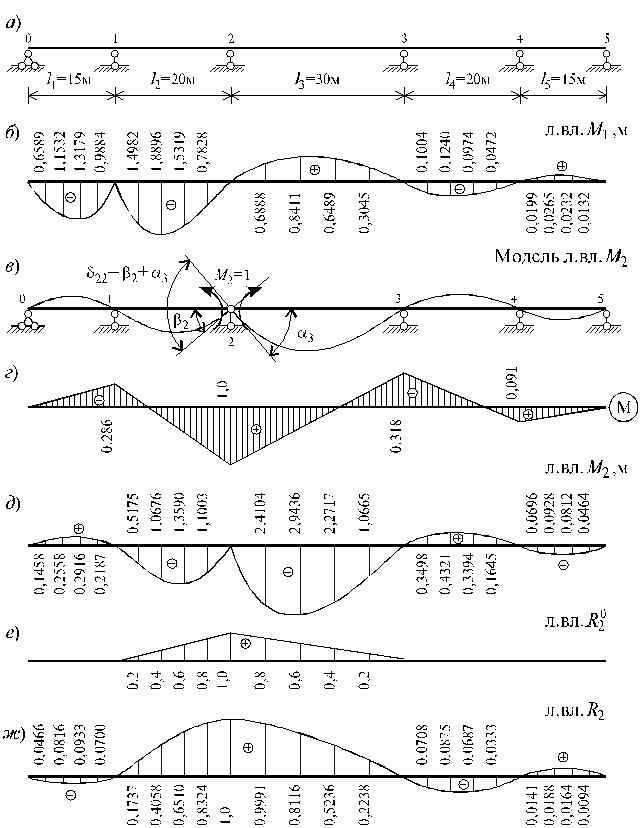
Рис.11.4

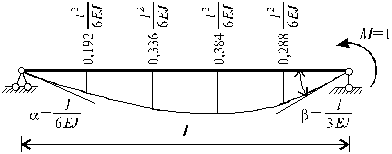
Рис.11.5

Решив эту систему, получим М₁ = -20/70 = -0,286кН×м. Подставим значение М₁ во второе и третье уравнения и умножим последнее на -5 и сложим со вторым, получим последовательно:

3 - 33×М₄ = 0 , т.е. М₄ = 3/33 = 0,091 кН×м и 2М₃ = -7/11, или М₃ = -7/22 = -0,318 кН×м.

По данным рис.11.3 подсчитаем взаимный угол поворота смежных сечений основной системы на опоре 2:

Используя рис.11.5, вычислим для каждого пролета ординаты эпюры моментов (упругой линии) основной системы . Расчеты будем вести в табличной форме (см. табл.11.1, где следует учесть, что ординаты линии влияния умножены на EJ).

Поясним методику заполнения таблицы.

Основная система расчленяется на балки на двух опорах при действии двух опорных моментов М_лев и М_прав.. По принципу независимости деформаций Бетти, прогибы балки подсчитываются независимо, как сумма прогибов от действия одного опорного момента (см. рис.11.5 или формулы 11.3):

,

где .

Таким образом, заполняются столбцы 3, 4 и 5 таблицы 11.1. В столбце 6 записываются ординаты линии влияния М₂, подсчитанные по формуле (11.10). На рис.11.5, д приведена линия влияния М₂.

Для построения линий влияния изгибающих моментов и поперечных сил в сечении неразрезной балки используются зависимости:

; (11.12)

(11.13)

где и - ординаты эпюр М_k и Q_k от внешней нагрузки в сечении к балки пролетом l_n на двух шарнирных опорах; M_n и M_n-1 - линии влияния опорных моментов неразрезной балки.

Таблица 11.1

Часть балки	Сечение	Момент на опоре приложен слева, M^лев^.	Момент на опоре приложен справа, M^прав^.	Момент на опоре приложен и слева и справа	Ординаты линии влияния, М2
Пролет 0-1	0 0,2 0,4 0,6 0,8 1,0	0 0 0 0 0 0	0 -2,0592 -3,6063 -4,1184 -3,0888 0	0 -2,0592 -3,6063 -4,1184 -3,0888 0	0 0,1458 0,2551 0,2916 0,2187 0
Пролет 1-2	0 0,2 0,4 0,6 0,8 1,0	0 -5,4912 -7,3216 -6,4046 -3,6608 0	0 12,800 22,400 25,600 19,200 0	0 7,3083 15,078 19,194 15,539 0	0 -0,1575 -1,0676 -1,3590 -1,1003 0
Пролет 2-3	0 0,2 0,4 0,6 0,8 1,0	0 43,200 57,600 50,400 28,800 0	0 -9,158 -16,027 -18,317 -13,738 0	0 34,042 41,573 32,083 15,062 0	0 -2,4104 -2,9436 -2,2717 -1,0665 0
Пролет 3-4	0 0,2 0,4 0,6 0,8 1,0	0 -6,1056 -8,1408 7,1232 4,0704 0	0 1,1648 2,0384 2,3296 1,7472 0	0 -4,9408 -6,1024 -4,7936 -2,3232 0	0 0,3498 0,4321 0,3394 0,1645 0
Пролет 4-5	0 0,2 0,4 0,6 0,8 1,0	0 0,9828 1,3104 1,1466 0,6552 0	0 0 0 0 0 0	0 0,9828 1,3104 1,1466 0,6552 0	0 -0,0696 -0,0928 -0,0812 -0,0464 0

Ординаты линии влияния опорной реакции R_n подсчитываются по формуле:

, (11.14)

где - линия влияния реакции шарнирной балки n, если эту эпюру рассматривать как общую для двух простых балок пролетом l_n и l_n+1.

На рис.11.3, е, ж приведены линии влияния опорных реакций и для неразрезной балки, приведенной на рис.11.3, а.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00