Лекции

 

 

Главная

 

64. Балка на упругом основании

 

64.1. Дифференциальное уравнение оси изогнутой балки,

лежащей на сплошном упругом основании

 

В инженерной практике часто встречаются балочные элементы конструкций, лежащие на сплошном упругом основании. К таким конструкциям могут быть отнесены шпалы железнодорожного пути, ленточные фундаменты зданий, фундаменты плотин, опирающиеся на грунты, разного рода трубопроводы, уложенные на грунт или внутрь его и др. Кроме того, к таким конструкциям относятся также и рельсы, у которых число опор бесконечно вели­ко, а расстояние между ними мало по сравнению с длиной.

В машиностроении и различных других областях техники для многих конструкций в эксплуатационном режиме, находящихся в условиях сплошного контакта с другими изделиями, можно применить расчетную схему балки на упругом основании.

При расчетах таких элементов предполагается, что грунт обладает упругими свойствами и его деформация пропорциональна приложенной нагрузке. Кроме этой основной предпосылки, при расчете балок на упругом основании принимаются и другие допущения:

- трение между основанием и балкой отсутствует;

- между опорной поверхностью балки и основанием имеется неразрывная связь, вследствие чего в основании могут возникнуть растягивающие усилия;

- упругое основание по всей длине балки однородно и ширина постели балки постоянная;

Расчет балки на упругом основании в строгой постановке сводится к решению контактной задачи между конструкцией и осно­ванием. Сложность решения контактных задач в строгой постановке общеизвестна. Поэтому для решения инженерных задач, связанных с расчетом балки применяются приближенные подходы, суть которых заключается в следующем.

Предварительно устанавливается зависимость между реактивным отпором и осадкой поверхности основания. Одной из наиболее распространенных гипотез является гипотеза о пропорциональной зависимости между реакцией и осадкой - гипотеза Винклеровского основания.

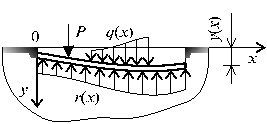
Рис. 64.1

 

На рис.64.1 показана деформация балки от внешней нагрузки, распределенной по произвольному закону. Реакция со стороны ос­нования в произвольной точке, при соблюдении условий проскальзывания  на контактной поверхности между подошвой балки и основанием, принимается пропорциональной прогибу:

где r(x) - реакция основания, приходящаяся на единицу длины балки, (Н/м); y(x) - просадка основания; ; b - ширина подошвы балки; k1 - коэффициент, характеризующий жесткость ос­нования и называемый коэффициентом податливости ос­нования или коэффициентом постели, [Па/м].

Этот коэффициент представляет собой отпор основания, при­ходящийся на 1 м2 площади при просадке, равной единице. Знак минус в выражении (64.1) означает, что реакция противоположна направлению просадки.

Значения коэффициента постели k1 для некоторых грунтовых и скальных оснований приведены в таблице 64.1.

Балка, лежащая на сплошном упругом основании, представляет собой статически неопределимую систему, так как одного условия равновесия – равенства внешней нагрузки всей общей реакции основания – недостаточно для установления закона распределения этой реакции по длине балки и для определения усилий в сечениях. Интенсивность реакции в каждой точке связана с прогибом балки, поэтому для решения задачи необходимо найти уравнение изогнутой оси балки, затем по этому уравнению определить закон распределения реактивных сил.

Таким образом, со стороны основания на балку действует сплошная распределенная нагрузка интенсивностью r(x). Суммар­ная интенсивность распределенной нагрузки, приложенной к балке при произвольном значении x определяется:

где q(x) - приложенная к балке, заданная распределенная нагрузка (например, вес погонной длины балки).

                                                                                                                        

Таблица 64.1. Значения коэффициента постели k1 для различных грунтов

№

Материал основания

k1, МПа/м

1

Песок свеженасыпанны

Глина мокрая, размягченная

1-5

2

Грунты средней плотности:

песок слежавшийся;

гравий насыпной;

глина влажная

5-50

3

Грунты плотные:

песок и гравий, плотно слежавшийся;
щебень;

глина малой влажности

50-100

4

Грунты весьма плотные:

грунт песчано-глинистый,

искусственно уплотненный;

глина твердая;

100-200

5

Известняк, песчаник, мерзлота

200-1000

6

Твердая скала

10000-15000

 

Дифференциальное уравнение изгиба упругой балки в данном случае принимает вид:

или после подстановки (64.2) в (64.3) получим:

Физический смысл модели, приводящий к уравнению (64.4), может быть различен. Так, если основание принимать в виде упругого полупространства, взамен модели Винклеровского основания, из приближенных решений контактных задач, то коэффициент k имеет вид:

где Eo - модуль деформации грунта основания; m - коэффициент Пуассона.

В случае балки постоянного сечения интегрирование уравнения (64.4) не представляет особых затруднений. Вводится обозначение:

где β - называется коэффициентом относительной жесткости осно­вания, [1/м].

Тогда дифференциальное уравнение (64.4) принимает вид:

Решение уравнения (64.5) можно получить общими методами решения дифференциальных уравнений с постоянными коэффици­ентами, и оно имеет следующую структуру:

где Сj - произвольные постоянные, j = 1, 2, 3, 4; yj (x) - частное линейно - независимое решение соответствующего (17.5) однородно­го уравнения

y*(x) - частное решение неоднородного уравнения (64.5), зависящее от характера внешней нагрузки q(x).

Частное решение однородного уравнения (64.7) представляется в виде , подставляя которое в (64.7), получим характе­ристическое уравнение

Используя формулы Муавра для корней из комплексных чисел найдем четыре корня уравнения (64.8):

где i - мнимая единица (i = ).

Следовательно, решение вида (64.6) будет таким

Произвольные постоянные С1, С2, С3 и С4 находятся из гранич­ных условий для конкретной задачи, как и при расчете обычной балки.

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

 

Теоретическая механика   Сопротивление материалов

Прикладная механика  Детали машин  Теория машин и механизмов

 

 

 

 

00:00:00

 

Top.Mail.Ru