Главная
64.2. Анализ общего решения
дифференциального
уравнения изгиба балки на упругом основании
Как нетрудно
видеть из (64.9), общее решение включает выражения для затухающей и
возрастающей гармоник или, иными словами, для двух затухающих гармоник, одна из
которых затухает по направлению к правому концу балки, а другая - к
левому. Затухание здесь довольно быстрое. Чтобы установить его степень,
увеличим x на
π/β. Тогда
получим
Анализируя
полученный результат, приходим к выводу, что первое слагаемое получило
множитель 
,
а второе слагаемое 
.
Таким образом, при переходе к следующей полуволне значение первого слагаемого (64.10)
уменьшаются в 23,14 раза, а второго слагаемого - увеличивается во столько
же раз.
В случае
длинной балки члены уравнения, содержащие множитель 
,
для правого ее конца становятся очень большими. Так как в действительности там
деформации и внутренние силы имеют конечную величину,
то коэффициенты С3 и С4 при членах, содержащих множитель ,
должны быть очень малыми и для достаточно длинной балки практически обращаться
в нуль. В этом случае общее решение упрощается и получает вид
На расстоянии
трех полуволн 
от левого конца балки члены общего решения с
постоянными интегрирования С1 и С2
практически исчезнут. Поэтому балку длиной 
можно считать бесконечно длинной. Точнее ее
можно рассчитывать, как бесконечно длинную, поскольку уже в середине ее влияние
концевых граничных условий будет сказываться очень мало.
Практически принимают, что если 
,
то балка принимается бесконечно длинной (бесконечно
длинная балка).
К общему
решению (64.9) надо добавить частное решение 
,
зависящее от нагрузки 
.
Если нагрузка представляет собой алгебраический полином от x, то частное решение можно найти в виде
полинома той же степени методом неопределенных коэффициентов. В частности, для
линейной функции вида 
(рис.64.2), частное решение уравнения (64.5)
имеет вид
Рис. 64.2
При отсутствии
приложенной к балке нагрузки, т.е. при q = 0,
момент и поперечная сила на них равны нулю; этому вполне удовлетворяет частное
решение (64.12) и добавлять к нему общее решение не требуется. Следовательно, (64.12)
будет полным решением, и балка не будет изгибаться. Очевидно, что внутренние
силы в ней везде равны нулю.
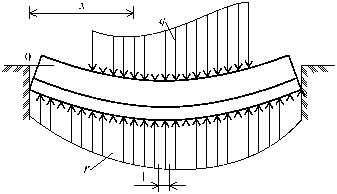
Рис. 64.3
Если балка
имеет на концах какие-либо закрепления, например опоры (рис.64.3), то в ней
появляются изгибающие моменты и кривизна оси, которые можно определить общим
методом нахождения произвольных постоянных общего решения по граничным условиям.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Теория машин и механизмов
