Главная

64.3. Расчет бесконечно длинной балки, нагруженной
сосредоточенной силой

Рассмотрим балку бесконечной длины, простирающуюся в области , нагруженную в сечении с абсциссой x сосредоточенной силой P (рис.64.4). Дифференциальное уравнение изогнутой оси балки записывается аналогично (64.4):

где δ(x) - единичная функция Дирака.

Общее решение (64.13) записывается аналогично (64.9). Произвольные постоянные С₁, С₂, С₃ и С₄ определяются из граничных условий задачи:

при

при x=0, ;

C учетом (64.14) следует, что

Рис. 64.4

Из первого из условий (64.15) получим:

или

Следовательно, решение (64.13) запишется в виде:

Из (64.19) легко установить, что

C учетом второго условия (64.15) можно записать, что

откуда окончательно получим:

Подставляя (64.22) в (64.19), получим окончательную формулу по определению прогибов балки на упругом основании при действии сосредоточенной силы P в следующем виде:

Последовательно определяем выражение изгибающего момента и поперечной силы:

Если в выражениях (64.23)¸(64.25) принять Р = 1 кН, то эпюры y (0), M_z(0) и Q_y(0) можно трактовать, как линии влияния, соответственно, деформаций, изгибающих моментов и поперечных сил для сечения балки х = 0. Соответствующие эпюры приведены на рис.64.4.

Обратим внимание на тот факт, что согласно (64.25) наибольший изгибающий момент , возникающий под силой P при заданной жесткости балки EI_z , в большей степени зависит от жесткости основания k, т.к. коэффициент относительной жесткости основания β зависит от соотношения k и EI_z . Например, в случае, если балка лежит на жестком основании (k), то ; и, наоборот, в случае, если балка лежит на мягком основании (k), то . Простым подтверждением этого явления может служить то, что железнодорожные рельсы, уложенные на жесткое основание, могут безболезненно выдерживать довольно значительные поездные нагрузки. В то же время, те же рельсы, уложенные на слабое основание, либо, если рельс "провисает" (т.е. пространство между шпалами содержит пустоты), могут разрушиться при значительно меньших нагрузках.

64.4. Расчет балки бесконечной длины, нагруженной
системой сосредоточенных сил

Рассмотрим решение следующей задачи. Предположим, что на балку бесконечной длины в точках с абсциссами x_j (j = 1, 2,..., N) приложена система сосредоточенных сил P₁, P₂, P₃,...,P_n (рис.64.5).

Рис. 64.5

Рассматривая решение поставленной задачи, на примере рельса верхнего строения пути в качестве балки, лежащей на сплошном упругом основании при действии системы сосредоточенных грузов P₁, P₂, P₃, ... , P_n , передающихся на путь от подвижного состава.

Железнодорожный путь должен отвечать требованиям прочности, жесткости и устойчивости при воздействии на него подвижного состава.

Напряжения и деформации, возникающие в опасных сечениях конструкции верхнего строения пути должны удовлетворять условиям прочности и жесткости, т.е.

где , y_max - соответственно, максимально возможное значение напряжений и прогибов конструкции в опасных сечениях; , - предельно допустимые величины напряжений и прогибов.

В данном случае формулы по определению прогибов, изгибающих моментов и поперечных сил в сечениях с координатами x_n (n = 1, 2, ... , N) на основании теоремы о независимости действия внешних сил в упругих системах и теоремы о взаимности можно записать в виде

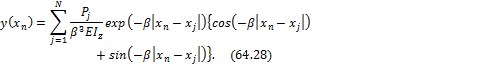
Последовательно определяем выражение изгибающего момента и поперечной силы:

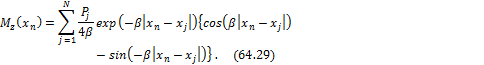
По максимальному значению момента, вычисляемому по (64.29):

в опасном поперечном сечении рельса в опасных точках вычисляется максимальное значение нормальных напряжений:

где W_z - момент сопротивления поперечного сечения рельса пути.

Прочность рельса пути считается обеспеченной, если выполняется условие

где R - расчетное сопротивление материала конструкции инвентарного верхнего строения пути.

Основные геометрические характеристики стандартных рельсов приведены в таблице 64.2.

Таблица 64.2. Основные геометрические характеристики стандартных рельсов

Геометрические характеристики		Тип рельсов
		Р38	Р43	Р50	Р65	Р75
		ГОСТ
		3542-47	7173-54	7174-75	8161-75	16210-77
Моменты инерции, 10^-8 м^4	Jz Jy	1222,5 209,3	1489,0 260,0	2011,0 375,0	3548,0 569,0	4490,0 661,0
Масса пог.м, кг	q	38,4	44,7	51,7	64,7	74,4
Моменты сопротивления относительно осей, 10^-6 м^3	Wz^низ Wz^гол Wy^под	182,0 180,3 36,7	208,3 217,3 45,6	248,0 286,0 57,1	358,0 435,0 76,3	509,0 432,0 88,0
Основные размеры сечения рельса, мм	H bпод hгол bгол 𝛿	135,0 114,0 40,0 68,0 13,0	140,0 114,0 42,0 70,0 14,5	152,0 132,0 42,0 71,9 16,0	180,0 150,0 45,0 75,0 18,0	192,0 160,0 48,5 75,0 20,0
Площадь сечения, 10^-4 м^2	A	49,1	57,0	65,9	82,6	95,1

64.5. Расчет элементов верхнего строения железнодорожного пути как

балки бесконечной длины на упругом основании

Пусть требуется определить прогибы и внутренние усилия в элементах железнодорожного пути. Характеристика пути: рельсы типа Р43; шпалы сосновые: длина шпалы 2,7 м, ширина 0,25 м; балласт песчаный с коэффициентом постели k₁ = 50 МПа (см. табл.64.1), площадь подкладки ω= 4,64∙10^-2 м^{2 ;} локомотив -тепловоз серии ТЭЗ с нагрузками от колес на рельс (105 + 105 + 105 + 105 + 105 + 105) кН с расстояниями между колесами (2,1 + 2,1 + 4,4 + 2,1 + 2,1) м (рис.64.6).

Рис. 64.6

Решение:

1. Определение прогибов и внутренних усилий

Последовательно вычисляем или находим по таблицам все необходимые геометрические и жесткостные расчетные характеристики для заданной системы:

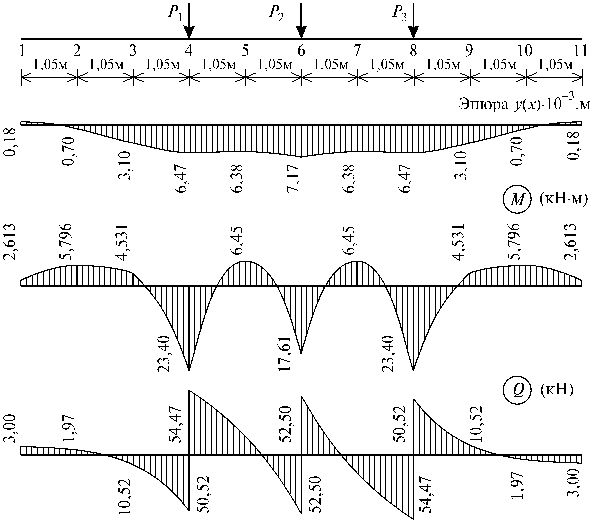
Рис. 64.7

I_z = 1,489∙10^-5 м⁴; W_z = 2,083∙10^-4 м³; (см. табл.64.2)

EI_z = 2,1∙10¹¹∙1,489∙10^-5 = 3,127∙10⁶ Нм²;

k = k₁∙b = 50∙10⁶∙0,14 = 7,0∙10⁶ Па.

Площадь полушпалы Ω = l×b/2 = 2,7×0,25/2 = 0,3375 м².

Определим м. Таким образом, в расчете будем учитывать нагрузки лишь от трех колес локомотива.

Разбиваем балку на участки в точках 1, 2,..., 11. На балку действует система сосредоточенных грузов Р₁ = Р₂ = Р₃ = 105 кН, приложенных в сечениях 4, 6 и 8 системы (рис.64.7, а).

Расчеты будем вести в табличной форме (см. табл.64.4 - 64.6), по формулам (64.28)¸(64.30), для чего в каждом сечении определяется параметр βx. По этому параметру в табл.64.3 находятся соответствующие значения специальных функций от действия отдельно каждой из нагрузок. Остальное ясно из таблиц 64.4 - 64.6.

Таблица 64.3

βx
0,0	1,0000	1,0000	1,0000
0,1	0,9907	0,8100	0,9003
0,2	0,9651	0,6398	0,8024
0,3	0,9267	0,4888	0,7077
0,4	0,8784	0,3564	0,6174
0,5	0,8231	0,2415	0,5323
0,6	0,7628	0,1431	0,4530
0,7	0,6997	0,0599	0,3708
p/4	0,6448	0,0000	0,3224
0,8	0,6354	-0,0093	0,3131
0,9	0,5712	-0,0657	0,2527
1,0	0,5083	0,1108	0,1988
1,1	0,4476	-0,1457	0,1510
1,2	0,3899	0,1716	0,1091
1,3	0,3355	-0,1897	0,0729
1,4	0,2849	-0,2011	0,0419
1,5	0,2384	-0,2068	0,0158
p/2	0,2079	-0,2079	0,0000
1,6	0,1959	-0,2077	-0,0059
1,7	0,1576	-0,2047	-0,0235
1,8	0,1234	-0,1985	-0,0376
1,9	0,0932	-0,1899	-0,0484
2,0	0,0667	-0,1794	-0,0563
2,1	0,0439	-0,1675	-0,0618
2,2	0,0244	-0,1548	-0,0652
2,3	0,0080	-0,1416	-0,0668
3π/4	0,0000	-0,1340	-0,0670
2,4	-0,0056	-0,1282	-0,0669
2,5	-0,0166	0,1149	-0,0658
2,6	-0,0254	-0,1019	-0,0636
2,7	-0,0320	-0,0895	-0,0608
2,8	-0,0369	-0,0777	-0,0573
2,9	0,0403	-0,0666	-0,0534
3,0	-0,04226	-0,05632	-0,04929
3,1	-0,04314	-0,04688	-0,04501
π	-0,04321	-0,04321	-0,04321
3π/2	-0,00898	0,00898	0,0000
2π	0,00187	0,00187	0,00187

Таблица 64.4

№ сеч.	Расстояние x до сечения от нагрузки, м (в скобках значение аргумента βx			Значения функции ηi в соответствующих точках от действия нагрузки				10^-3 м
	P1	P2	P3	P1	P2	P3
1	-3,15 (2,7)	-5,25 (4,5)	-7,35 (6,3)	-0,0334	-0,0123	0,0019	-0,0438	-0,2845
2	-2,10 (1,8)	-4,20 (3,6)	-6,30 (5,4)	0,1181	-0,0357	-0,0003	0,0821	0,5323
3	-1,05 (0,9)	-3,15 (2,7)	-5,25 (4,5)	0,5659	-0,0334	-0,0123	0,5202	3,3738
4	0,00 (0,0)	-2,10 (1,8)	-4,20 (3,6)	1,0000	0,1181	-0,0357	1,0823	7,0194
5	1,05 (0,9)	-1,05 (0,9)	-3,15 (2,7)	0,5659	0,5659	-0,0334	1,0985	7,1240
6	2,10 (1,8)	0,00 (0,0)	-2,10 (1,8)	0,1181	1,0000	0,1181	1,2363	8,0177
7	3,15 (2,7)	1,05 (0,9)	-1,05 (0,9)	-0,0334	0,5659	0,5659	1,0985	7,1240
8	4,20 (3,6)	2,10 (1,8)	0,00 (0,0)	-0,0357	0,1181	1,0000	1,0824	7,0194
9	5,25 (4,5)	3,15 (2,7)	1,05 (0,9)	-0,0123	-0,0334	0,5659	0,5202	3,3737
10	6,30 (5,4)	4,20 (3,6)	2,10 (1,8)	-0,0003	-0,0357	0,1181	0,0821	0,5323
11	7,35 (6,0)	5,25 (4,5)	3,15 (2,7)	0,0019	-0,0123	-0,0334	-0,0438	-0,2845

Таблица 64.5

№ сеч.	Расстояние x до сечения от нагрузки, м (в скобках значение аргумента βx			Значения функции ψi в соответствующих точках от действия нагрузки				кНм
	P1	P2	P3	P1	P2	P3
1	-3,15 (2,7)	-5,25 (4,5)	-7,35 (6,3)	-0,0865	0,0087	0,0016	-0,0762	-2,312
2	-2,10 (1,8)	-4,20 (3,6)	-6,30 (5,4)	-0,1972	-0,0108	0,0061	-0,2020	-6,130
3	-1,05 (0,9)	-3,15 (2,7)	-5,25 (4,5)	-0,0699	-0,0865	0,0087	-0,1477	-4,481
4	0,00 (0,0)	-2,10 (1,8)	-4,20 (3,6)	1,0000	-0,1972	-0,0108	0,7919	24,031
5	1,05 (0,9)	-1,05 (0,9)	-3,15 (2,7)	-0,0699	-0,0699	-0,0865	-0,2263	-6,866
6	2,10 (1,8)	0,00 (0,0)	-2,10 (1,8)	-0,1972	1,0000	-0,1972	0,6054	18,374
7	3,15 (2,7)	1,05 (0,9)	-1,05 (0,9)	-0,0865	-0,0699	-0,0699	-0,2262	-6,866
8	4,20 (3,6)	2,10 (1,8)	0,00 (0,0)	-0,0108	-0,1972	1,0000	0,7919	24,031
9	5,25 (4,5)	3,15 (2,7)	1,05 (0,9)	-0,0087	-0,0865	-0,0699	-0,1477	-4,481
10	6,30 (5,4)	4,20 (3,6)	2,10 (1,8)	0,0061	-0,0108	-0,1972	-0,2020	-6,130
11	7,35 (6,0)	5,25 (4,5)	3,15 (2,7)	0,0016	-0,0087	-0,0865	-0,0762	-2,312

Таблица 64.6

№ сеч.	Расстояние x до сечения от нагрузки, м (в скобках значение аргумента βx			Значения функции ψi в соответствующих точках от действия нагрузки				кН
	P1	P2	P3	P1	P2	P3
1	-3,15 (2,7)	-5,25 (4,5)	-7,35 (6,3)	0,0599	0,0018	-0,0017	0,0600	3,151
2	-2,10 (1,8)	-4,20 (3,6)	-6,30 (5,4)	0,0395	0,0233	-0,0029	0,0599	3,148
3	-1,05 (0,9)	-3,15 (2,7)	-5,25 (4,5)	-0,2480	0,0599	0,0018	-0,1863	-9,779
4	0,00 (0,0)	-2,10 (1,8)	-4,20 (3,6)	-1,0000	0,0395	0,0233	-0,9371	-49,199
4'	0,00 (0,0)	-2,10 (1,8)	-4,20 (3,6)	1,0000	0,0395	0,0233	1,0628	55,797
5	1,05 (0,9)	-1,05 (0,9)	-3,15 (2,7)	0,2480	-0,2480	0,0599	0,0599	3,1448
6	2,10 (1,8)	0,00 (0,0)	-2,10 (1,8)	-0,0395	-1,0000	0,0395	-1,0000	-52,500
6'	2,10 (1,8)	0,00 (0,0)	-2,10 (1,8)	-0,0395	1,0000	0,0395	1,0000	52,500
7	3,15 (2,7)	1,05 (0,9)	-1,05 (0,9)	-0,0599	0,2480	-0,2480	-0,0599	-3,1448
8	4,20 (3,6)	2,10 (1,8)	0,00 (0,0)	-0,0233	-0,0395	-1,0000	-1,0628	-55,797
8’	4,20 (3,6)	2,10 (1,8)	0,00 (0,0)	-0,0233	-0,0395	1,0000	0,9371	49,199
9	5,25 (4,5)	3,15 (2,7)	1,05 (0,9)	-0,0018	-0,0599	0,2480	0,1863	9,779
10	6,30 (5,4)	4,20 (3,6)	2,10 (1,8)	0,0029	-0,0233	-0,0395	-00599	-3,148
11	7,35 (6,0)	5,25 (4,5)	3,15 (2,7)	0,0017	-0,0018	-0,0599	-0,0600	-3,151

По этим результатам построены эпюры прогибов, изгибающих моментов и поперечных сил (см. рис.64.7, б, в, г).

2. Определение напряжений в элементах верхнего строения пути

Напряжения от изгиба в подошве рельса:

Значения напряжений на шпале под подкладкой и на баласте под шпалой будут соответственно равны:

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00