Главная
64.6. Расчет коротких
балок на упругом основании.
Функции
Крылова
Рис. 64.8
Значительно более сложным оказывается решение
для коротких балок, когда требуется учесть условия на обоих концах балки. К
таким балкам относится, например, рельсовый путь на шпалах (рис.64.8). Для
коротких балок нельзя использовать решения, полученные для
балок бесконечной длины и требуется исходить из общего интеграла (17.9),
содержащего четыре произвольные постоянные интегрирования. Для решения обычно
пользуются нормальными фундаментальными функциями уравнения (64.5). Эти функции
называемые функциями Крылова, являются решениями однородного уравнения (64.5) и
удовлетворяют специальным условиям при x = 0.
Cоставим
следующую таблицу, в которой сведены начальные значения функций Крылова и их
производных:
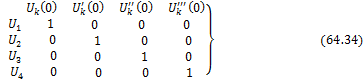
Так как во всех клетках этой таблицы стоят
нули, лишь на главной диагонали единицы, то система частных решений Uk , называется системой с
единичной матрицей. Эти решения суть:
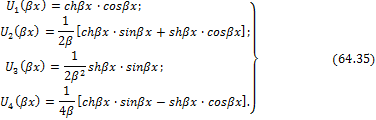
Следует отметить, что производные функций
Крылова (64.35) выражаются снова через те же функции, причем:
Таким образом, общий интеграл уравнения (64.9)
может быть представлен через функции Крылова:
Постоянные интегрирования C1 , C2 , C3 , C4 имеют здесь совершенно
определенный смысл. Действительно, если положить x = 0, и воспользоваться свойством (64.34) введенных
функций, получим:
Таким
образом:
Формула (64.39) представляет общий интеграл
уравнения (64.5). Постоянные интегрирования имеют здесь простой смысл: это начальные
(при x = 0) значения
искомой функции и ее производные. Поэтому, метод
интегрирования дифференциальных уравнений, основанный на формуле (64.39), и
широко применяемый в строительной механике, называется методом начальных параметров.
Согласно метода
начальных параметров, балка разбивается на участки. Подставив (64.38) в (64.39),
получим функцию прогибов на I участке балки:
Пользуясь приведенными в (64.36) правилами
дифференцирования от функций прогибов (64.40) переходим к углам поворота 
и
далее по формулам (64.25), (64.26) к внутренним усилиям на I участке:
Функцию 
продолжаем на второй и последующие
участки. Приращения 
этой
функции будут зависеть от приращений внутренних сил 
, 
и интенсивности нагрузки на границах
между участками 
. Добавляя эти приращения к функции прогибов,
углов поворота, изгибающих моментов и поперечных сил,
получим универсальные формулы:
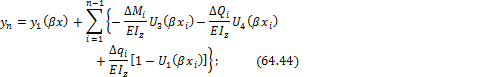
здесь для краткости обозначено 
; 
-
абсцисса i-ой границы между участками.
Как и в обычной балке, в начале координат
часть начальных параметров бывает известна, а
остальные определяются из граничных условий, формируемых для противоположного
конца стержня.
С целью облегчения вычислений при выполнении практических
расчетов балок на упругом основании в таблице 64.7 приводятся значения
тригонометрических, гиперболических функций и функций Крылова при заданном
аргументе.
Таблица 64.7
|
βz |
sinβz |
cosβz |
shβz |
chβz |
|
βU2(βz) |
β2U3(βz) |
β3U4(βz) |
|
0,0 |
0,0000 |
1,0000 |
0,0000 |
1,0000 |
1,0000 |
0,0000 |
0,0000 |
0,0000 |
|
0,1 |
0,0998 |
0,9950 |
0,1002 |
1,0050 |
0,9999 |
0,1000 |
0,0050 |
0,0002 |
|
0,2 |
0,1987 |
0,9801 |
0,2013 |
1,0201 |
0,9998 |
0,1999 |
0,0200 |
0,0024 |
|
0,3 |
0,2955 |
0,9553 |
0,3045 |
1,0453 |
0,9986 |
0,2999 |
0,0450 |
0,0045 |
|
0,4 |
0,3894 |
0,9210 |
0,4108 |
1,0811 |
0,9957 |
0,3997 |
0,0800 |
0,0107 |
|
0,5 |
0,4794 |
0,8776 |
0,5211 |
1,1276 |
0,9896 |
0,4989 |
0,1249 |
0,0208 |
|
0,6 |
0,5646 |
0,8253 |
0,6367 |
1,1855 |
0,9784 |
0,5974 |
0,1797 |
0,0360 |
|
0,7 |
0,6442 |
0,7648 |
0,7586 |
1,2552 |
0,9600 |
0,6944 |
0,2443 |
0,0571 |
|
π/4 |
0,7071 |
0,7071 |
0,8687 |
1,3246 |
0,9366 |
0,7754 |
0,3071 |
0,0806 |
|
0,8 |
0,7173 |
0,6967 |
0,8881 |
1,3374 |
0,9318 |
0,7890 |
0,3185 |
0,0851 |
|
0,9 |
0,7833 |
0,6216 |
1,0265 |
1,4331 |
0,8908 |
0,8803 |
0,4020 |
0,1211 |
|
1,0 |
0,8415 |
0,5403 |
1,1752 |
1,5431 |
0,8337 |
0,9667 |
0,4944 |
0,1659 |
|
1,1 |
0,8912 |
0,4536 |
1,3356 |
1,6685 |
0,7568 |
1,0464 |
0,5951 |
0,2203 |
|
1,2 |
0,9320 |
0,3624 |
1,5095 |
1,8107 |
0,6562 |
1,1173 |
0,7034 |
0,2851 |
|
1,3 |
0,9636 |
0,2675 |
1,6984 |
1,9709 |
0,5272 |
1,1767 |
0,8183 |
0,3612 |
|
1,4 |
0,9854 |
0,1700 |
1,9043 |
2,1509 |
0,3656 |
1,2216 |
0,9382 |
0,4489 |
|
1,5 |
0,9975 |
0,0707 |
2,1293 |
2,3524 |
0,1663 |
1,2485 |
1,0620 |
0,5490 |
|
π/2 |
1,0000 |
0,0000 |
2,3013 |
2,5092 |
0,0000 |
1,2546 |
1,1507 |
0,6273 |
|
1,6 |
0,9996 |
-0,0292 |
2,3756 |
2,5775 |
-0,0753 |
1,2536 |
1,1873 |
0,6615 |
|
1,7 |
0,9917 |
-0,1288 |
2,6456 |
2,8283 |
-0,3643 |
1,2320 |
1,3118 |
0,7864 |
|
1,8 |
0,9738 |
-0,2272 |
2,9422 |
3,1075 |
-0,7060 |
1,1788 |
1,4326 |
0,9236 |
|
1,9 |
0,9463 |
-0,3233 |
3,2682 |
3,4174 |
-1,1049 |
1,0886 |
1,5463 |
1,0726 |
|
2,0 |
0,9093 |
-0,4161 |
3,6269 |
3,7622 |
-1,5655 |
0,9559 |
1,6420 |
1,2320 |
|
2,1 |
0,8632 |
-0,5048 |
4,0219 |
4,1443 |
-2,0920 |
0,7736 |
1,7359 |
1,4019 |
|
2,2 |
0,8084 |
-0,5885 |
4,4571 |
4,5679 |
-2,6882 |
0,5348 |
1,8016 |
1,5789 |
|
2,3 |
0,7457 |
-0,6663 |
4,9370 |
5,0372 |
-3,3563 |
0,2334 |
1,8408 |
1,7614 |
|
3π/4 |
0,7071 |
-0,7071 |
5,2280 |
5,3228 |
-3,7634 |
0,0335 |
1,8484 |
1,8651 |
|
2,4 |
0,6754 |
-0,7374 |
5,4662 |
5,5569 |
-4,0976 |
-0,1388 |
1,8459 |
1,9460 |
|
2,5 |
0,5985 |
-0,8011 |
6,0502 |
6,1323 |
-4,9126 |
-0,5883 |
1,8105 |
2,1292 |
|
2,6 |
0,5155 |
-0,8569 |
6,6947 |
6,7690 |
-5,8003 |
-1,1236 |
1,7256 |
2,3065 |
|
2,7 |
0,4274 |
-0,9041 |
7,4063 |
7,4735 |
-6,7568 |
-1,7509 |
1,5827 |
2,4725 |
|
2,8 |
0,3390 |
-0,9422 |
8,1919 |
8,2527 |
-7,7757 |
-2,4604 |
1,3885 |
2,6290 |
|
2,9 |
0,2392 |
-0,9710 |
9,0596 |
9,1146 |
-8,8503 |
-3,3083 |
1,0835 |
2,7443 |
|
3,0 |
0,1411 |
-0,9900 |
10,0179 |
10,0677 |
-9,9670 |
-4,2486 |
0,7068 |
2,8346 |
|
3,1 |
0,0416 |
-0,9991 |
11,0765 |
11,1215 |
-11,1114 |
-5,3019 |
0,2304 |
2,8822 |
|
π |
0,0000 |
-1,0000 |
11,5487 |
11,5920 |
-11,5920 |
-5,7960 |
0,0000 |
2,8872 |
64.7. Расчет шпалы
рельсового пути, как короткой балки
на
упругом основании
Пусть
требуется определить прогибы и внутренние усилия в железобетонных шпалах E = 3,05∙1010 Н/м2, длиной 2l = 2,7 м,
с размерами поперечного сечения b × h = 0,25×0,18 м2, лежащей на балластном слое щебня k1 = 75 МПа
(см. табл.64.1), нагруженной двумя силами P = 210 кН каждый, приложенных на расстоянии a = 0,54 м от ее концов (рис.64.8).
Решение:
1. Расчет
начальных параметров
Последовательно
вычисляем все необходимые геометрические и жесткостные
расчетные характеристики для заданной системы:
Поместим
начало системы координат xy в центре тяжести левого крайнего
сечения шпалы. Граничные условия задачи в начальном сечении при x = 0 запишем в виде:
Согласно (64.40)¸(64.43)
запишем функции прогибов, углов поворота и внутренних усилий для I участка (0≤x≤a):
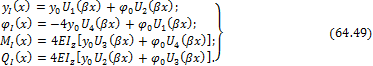
Составим
соответствующие выражения для II участка (
), учтя, что на границе участков I
и II, т.е. при x = a и имеем скачок функции поперечной силы
на величину 
:
Для
определения y0 и φ0, используем симметричный характер нагружения балки относительно среднего сечения x = l, где имеем:
φ(l) = 0; Q(l) = 0.
Составим
следующую систему уравнений:
Cогласно (64.54) и (64.55),
учитывая, что
βl= 1,06×1,35 » 1,5; β(l-a) = 1,06×(1,35 - 0,54) = 0,9,
с учетом
данных таблицы 64.7, получим:
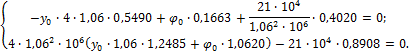
После ряда
преобразований приходим к системе:
корни которой принимают значения:
В качестве условия проверки правильности вычисления значений начальных
параметров, подставим их значения в (64.54)
и (64.55), получим:
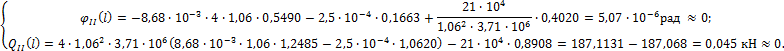
Следовательно,
величины y0 и φ0 определены верно.
2. Определение
прогибов, углов поворота и внутренних усилий
Разобьем балку
на 10 участков. Используем симметрию задачи, поэтому будем рассматривать только
половину балки, т.е. сечения 0, 1, 2, 2’, 3, 4, 5 (см. рис.64.9, а). Расчеты будем вести в табличной
форме (см. табл.64.8). Поэтому, согласно (64.52), запишем выражения прогибов, углов поворота и
внутренних усилий для I и II участков:
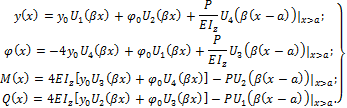
Участок I.
Сечение 0, x = 0:
y0 = 8,68∙10-3
м; φ0 = -2,5∙10-4
рад; M0 = 0;
Q0 = 0.
Cечение 1, x = 0,27 м.
Cечение 2, x = 0,54 м.
Участок II.
Cечение 2’, x = 0,54 м.
Cечение 3, x = 0,81 м.
Сечение 4, x = 1,08 м.
Сечение 5, x = 1,35 м.
Результаты
расчетов внесены в таблицу 64.8 и по этим значениям построены эпюры
прогибов, углов поворота, изгибающих моментов и поперечных сил (см. рис.64.9, б, в, г).
Таблица
64.8
|
№ сеч. |
x |
βx |
β(x-a) |
U1 |
U2 |
U3 |
U4 |
y, 10-2
м |
φ, 10-3 рад |
M, кНм |
Q, кН |
|
0 |
0 |
0 |
- |
1,000 |
0,000 |
0,000 |
0,000 |
8,680 |
-0,250 |
0,000 |
0,000 |
|
1 |
0,27 |
0,3 |
- |
0,999 |
0,299 |
0,045 |
0,004 |
8,597 |
-0,251 |
6,50 |
45,82 |
|
2 |
0,54 |
0,6 |
- |
0,978 |
0,597 |
0,179 |
0,036 |
8,352 |
-1,570 |
25,87 |
90,90 |
|
2’ |
0,54 |
0,6 |
0 |
0,978 |
0,597 |
0,179 |
0,036 |
8,352 |
-1,570 |
25,87 |
-119,1 |
|
3 |
0,81 |
0,9 |
0,3 |
0,891 |
0,880 |
0,402 |
0,121 |
7,738 |
-2,413 |
1,71 |
-76,33 |
|
4 |
1,08 |
1,2 |
0,6 |
0,656 |
1,117 |
0,703 |
0,285 |
7,143 |
-1,938 |
-17,67 |
-36,98 |
|
5 |
1,35 |
1,5 |
0,9 |
0,166 |
1,249 |
1,062 |
0,549 |
6,904 |
0,000 |
-22,85 |
-0,04 |
Рис. 64.9
Вопросы для самопроверки
- Раскройте
суть гипотезы Винклеровского основания.
- Поясните
физический смысл коэффициента постели.
- Дайте
определение относительно коротких и балок
бесконечной длины
- Подчеркните
отличительные особенности между дифференциальными уравнениями изгиба обычных
балок и балок на упругом основании.
- Какими
свойствами должны обладать функции Крылова.
-
Сформулируйте условия достаточной жесткости и прочности конструкций на упругом
основании.
- Что понимается под термином
«балка на упругом основании»?
- Сформулируйте предпосылки, на которых построен расчет
балок на упругом основании?
- Напишите общее выражение для
интенсивности нагрузки балки на упругом основании и сформулируйте смысл
параметров, входящих в это выражение?
- Получите дифференциальные
уравнения для прогибов и изгибающих моментов балки на упругом основании?
- Напишите уравнение для
изгибающих моментов балки на упругом основании по методу начальных параметров?
- Опишите технику написания
выражения для М балки на упругом основании по методу начальных параметров?
- Приведите дифференциальные
соотношения между функциональными коэффициентами А, В, С, D.
- Получите выражения для Q, р, р' путем дифференцирования выражения для М.
- Какие начальные параметры
входят в уравнения балки на упругом основании и как они находятся?
- Опишите технику решения задач
балки на упругом основании по методу начальных параметров?
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Теория машин и механизмов
