Главная

65. Устойчивость сооружений

65.1. Предмет и задачи устойчивости

Кроме прочности и жесткости, сооружение обязательно должно быть устойчивым. Это потому, что при потере устойчивости сооружение или разрушается, или становится непригодным для дальнейшей эксплуатации. Например, даже такой простейший элемент как прямолинейный длинный стержень при действии продольной сжимающей силы может резко изогнуться и потерять свою первоначальную прямолинейную форму. В практике строительства и эксплуатации различных сооружений (мостов, высотных зданий и др.) известны случаи их разрушения из-за потери устойчивости.

Устойчивость – это способность сооружения сохранять свое первоначальное положение или форму.

Положение сооружения или форма равновесия в нагруженном состоянии считаются устойчивыми, если при всяком, сколь угодно малом дополнительном возмущении, сооружение отклоняется от исследуемого положения или равновесного состояния, однако после исчезновения дополнительного возмущения полностью возвращается в исходное состояние (для упругих систем), или проявляет тенденцию к возвращению в исходное состояние (для упруго-пластических систем).

Положение сооружения или форма равновесия в нагруженном состоянии считаются неустойчивыми, если при каком-либо сколь угодно малом отклонении от исследуемого равновесном состоянии и после исчезновения возмущения сооружение не проявляет тенденцию к уменьшению получаемых отклонений, а иногда отклоняется еще далее - до нового положения или новой формы равновесного состояния.

Переход устойчивого сооружения в неустойчивое состояние называется потерей устойчивости. Граница перехода в неустойчивое состояние называется критическим состоянием. Сила, приводящая сооружение в критическое состояние, называется критической силой. Критическую силу будем обозначать P_кр.

Ответ на вопрос «устойчиво или неустойчиво сооружение?» является очень важной задачей, потому что для потери устойчивости сооружения, достигшего критического состояния, достаточно и незначительной причины. Если же процесс потери устойчивости начался, он идет очень быстро и приводит к резкому изменению первоначальной формы или разрушению частей или всего сооружения.

В соответствии с этим надо различать устойчивость положения сооружения и устойчивость форм равновесия в нагруженном состоянии.

Устойчивость положения – это способность сооружения сохранять свое положение. Например, при действии на подпорную стенку нагрузки q (рис. 65.1,а), относительно точки А создается опрокидывающий момент , от чего подпорная стенка может потерять устойчивость (рис. 65.1,б). Этому противостоит собственный вес подпорной стенки G, создающий удерживающий момент . Устойчивость системы зависит от соотношения этих моментов, так как при:

1)  – система устойчива;

2)  – система неустойчива;

3)  – система безразлична.

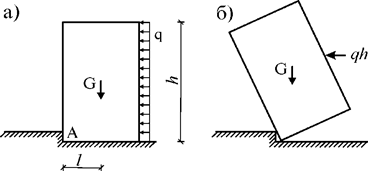
Рис. 65.1

Устойчивость формы – способность сооружения сохранять свою первоначальную форму.

Например, если верхний конец стержня с действующей продольной силой P немного отклонить в сторону (рис. 65.2,а), он при P<P_кр вернется в исходное положение. Такая система является устойчивой.

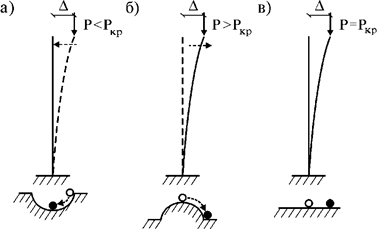
Рис. 65.2

Если же P>P_кр, перемещения стержня начинают возрастать (рис.65.2,б). Такая система в исходное состояние вернуться не может. Поэтому ее называют неустойчивой.

Если P=P_кр, система остается в безразличном состоянии (рис. 65.2,в).

Таким образом, в зависимости от величины приложенной нагрузки система может быть устойчивой, неустойчивой или безразличной. На рисунках 65.2,а-в показаны схематические аналоги устойчивой, неустойчивой и безразличной систем.

Потеря устойчивости делится на 2 рода.

Потеря устойчивости первого рода (потеря устойчивости по Эйлеру) связана с появлением нового вида деформации и характеризуется нарушением равновесия между нагрузкой и внутренними усилиями и свойственна только упругим системам. Она может быть трех типов:

– потеря устойчивости центрального сжатия (рис. 65.2,б);

– потеря устойчивости симметричной формы деформации (рис. 65.3,а, б);

– потеря устойчивости плоской деформации (рис. 65.3,в).

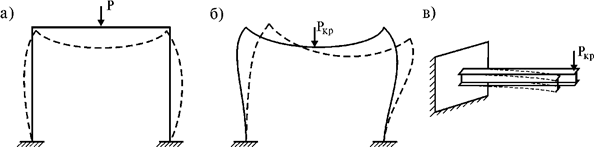
Рис. 65.3

Потеря устойчивости второго рода наблюдается при потере несущей способности всего сооружения и характеризуется резким возрастанием предыдущих деформаций. В этом случае равновесие между нагрузкой и внутренними усилиями нарушается даже без появления новых видов деформаций (рис. 65.4,а-в):

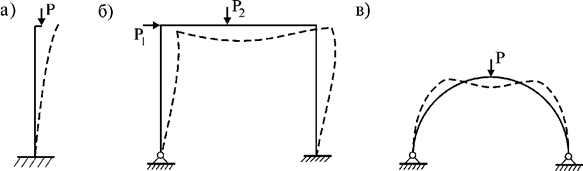
Рис. 65.4

Основной задачей теории устойчивости является определение критической силы P_кр. Поскольку потерявшее устойчивость сооружение обычно непригодно для дальнейшей эксплуатации, определять форму потери устойчивости сооружения во многих случаях не требуется. При этом наибольшее практическое значение имеет определение критических значений внешних сил при потере устойчивости системы по первому роду.

Если на систему действует несколько сил (рис. 65.5,а), определять их критические значения одновременно довольно трудно. Поэтому одну из сил (обычно наибольшую) принимают за основную и обозначают P, а остальные выражают через него (рис. 65.5,б). Тогда вместо определения нескольких критических сил можно определять только одну (наибольшую).

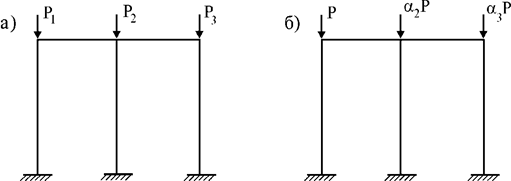
Рис. 65.5

65.2. Критерии определения устойчивости упругих систем

Расчеты на устойчивость проводят обособленно от расчетов на прочность, являющихся основными.

Исследование устойчивости ведутся при следующих допущениях:

- рассматривают только узловое приложение нагрузки, при этом поперечный изгиб стержней отсутствует;

- стержни рамы считают нерастяжимыми и несжимаемыми;

- расстояния между узлами при деформациях неизменяемые (это допущение применяют только при статическом методе расчета).

Расчет на устойчивость можно вести тремя методами: статическим, энергетическим и динамическим.

Статический метод основан на составлении уравнений статики. Суть статического метода заключается в следующем. Исследуемой системе задается отклоненная форма равновесия, совпадающая по характеру перемещений с ожидаемой новой формой равновесного состояния системы после потери устойчивости системы, и определяются значения рассматриваемых внешних нагрузок, способных удержать систему в новой форме равновесного состояния.

Значения внешних нагрузок, способных удержать систему в новом равновесном состоянии, при соблюдении граничных условий по исходному состоянию, является критическим.

Алгоритм статического метода состоит из трех этапов:

– задать системе малые перемещения;

– составить уравнения равновесия внешних и внутренних сил;

– из этих уравнений определить критическую силу.

В дальнейшем, здесь рассматривается решение задач теории устойчивости с применением только статического критерия, так как он является основным критерием при выполнении практических расчетов упругих консервативных систем.

В основе энергетического метода заложен известный принцип Лагранжа-Дирихле, согласно которому, если система находится в состоянии устойчивого равновесия, ее полная потенциальная энергия обладает минимумом по сравнению со всеми соседними состояниями системы; если в состоянии неустойчивого равновесия - то максимумом; а если в безразличном, т.е. критическом - то потенциальная энергия является постоянной величиной.

В общем случае изменение (вариацию) полной потенциальной энергии системы dU при переходе ее от рассматриваемого состояния к соседнему можно записать таким образом:

dU = dV - dT,

где dV - вариация потенциальной энергии внутренних сил; dT -вариация потенциальной энергии внешних сил.

Следовательно, критическое состояние системы, согласно энергетического критерия, определяется из условия

dU = 0   или   dV = dT.

Алгоритм энергического метода состоит из трех этапов:

– задать системе малые перемещения;

– определить приращения работ внешних и внутренних сил;

– из условия их равенства определить критическую силу.

Динамический метод основан на изучении колебаний системы. При решении задач устойчивости по динамическому методу исходят из предположения, что колеблющаяся система около своего положения равновесия, не способна возвращаться к первоначальному положению. Данное предположение равносильно утверждению, что в критическом состоянии спектр собственных частот рассматриваемой системы стремится к нулю, т.е.  = 0 (i = 1, 2, 3, ...). Здесь - собственная частота рассматриваемой системы при i-ой форме колебаний.

Следовательно, при решении задач по динамическому критерию составляется уравнение собственных колебаний заданной системы, далее определяется выражение частот собственных колебаний и из условия их равенства нулю определяется критическое значение внешних сил.

Так например, для сжатого осевой продольной силой P стержня постоянного поперечного сечения с распределенной массой, частота основного тона поперечных колебаний выражается формулой

,

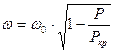где - собственная частота поперечных колебаний при отсутствии сжимающей силы, т.е. при P = 0.

Очевидно, что при , и период колебаний , т.е. стержень, колеблющийся около своего положения равновесия, не способен возвращаться к первоначальному состоянию.

Алгоритм динамического метода также состоит из трех этапов:

– задать системе малые перемещения;

– записать уравнение движения системы;

– из условия равенства нулю частоты собственных колебаний системы определить критическую силу.

65.3. Задача Эйлера

Рассмотрим решение задачи устойчивости упругого стержня, постоянного поперечного сечения, расположенной на двух шарнирно опертых концах, при действии продольной силы переменной величины Р (рис.65.6).Впервые эта задача была поставлена и решена Л. Эйлером в середине XVIII века.

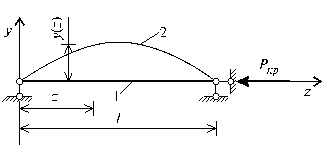
Рис.65.6

На начальном этапе действия постоянно возрастающей силы Р, очевидно, что в поперечных сечениях стержня возникают только продольно сжимающие силы и стержень испытывает сжатие, сохраняя прямолинейную форму деформированного состояния (1). Считая данную форму деформированного состояния в качестве начальной, предполагают, что при некотором значении внешней силы Р = P_кр стержень изогнется, т.е. в некотором новом равновесном состоянии принимает искривленную форму (2), изображенную на рис.65.6.

Обозначая величину прогибов стержня через y (z) в сечении, расположенном на расстоянии z от начала системы координат y z, значения изгибающих моментов в указанном поперечном сечении от действия внешней силы Р принимают значения

.

Из теории изгиба, при малых прогибах и пренебрегая продольными деформациями, деформированное состояние стержня за счет изгиба, описывается уравнением

. (1)

Принимая обозначение

, (2)

уравнение (1) можно представить в следующем виде:

. (3)

Решение (3) имеет следующий вид:

. (4)

Произвольные постоянные С₁ и С₂ определяются из граничных условий закрепления балки, т.е. y(0) = 0; y(l) = 0.

Из первого условия вытекает, что С₂ = 0, а из второго

. (5)

Последнее уравнение имеет два возможных решения: либо С₁ = 0, либо же .

В первом случае получается, что С₁ = С₂ = 0 и перемещения согласно (4) тождественно равны нулю, т.е. y = 0. Это решение очевидно соответствует первоначальному равновесному состоянию, которое нас не интересует. Во втором случае, т.е. предполагая, что С₁ ¹ 0, из (5) следует, что . Откуда следует, что , где n = 1,2,3,... С учетом выражения (13.2), получим . Наименьшая критическая сила получается при n=1:

. (6)

Эта сила носит название первой критической или эйлеровой силы. Решение (4) при С₁ ¹ 0 C₂ = 0 принимает вид .

При выполнении практических расчетов, как правило, определяется критическое значение внешней силы, соответствующее низшей форме потери устойчивости системы. Поэтому мы далее будем рассматривать решение задачи по определению только наименьшего значения критических сил.

Использовать этот метод для совокупности стержней, представляющих конструкцию в целом, затруднительно из-за громоздкости вычислений. Были предложены статические методы: метод сил и метод перемещений (на их основе - и другие способы). Метод перемещений считают более предпочтительным. Аналогично, как и при решении задач статики, метод перемещений эффективнее в том случае, когда имеется набор решений для элементарных состояний, взятых из таблиц характерных эпюр и формул определения их ординат.

65.4. Устойчивость стержней с различными
концевыми условиями их закрепления

Рассмотрим однопролетный упругий стержень постоянного поперечного сечения, по концам которого приложены сжимающие силы Р, всегда направленные параллельно оси недеформированного стержня. Поместим начало системы декартовых координат xyz в центре тяжести левого крайнего сечения. Ось z направим по продольной недеформированной оси стержня, а ось y - по направлению наименьшей жесткости поперечного сечения.

С целью введения различных условий закрепления в концевых сечениях стержня предполагается, что в новом равновесном (критическом) состоянии (2) в общем случае могут быть приложены поперечные силы и изгибающие моменты. Кроме того, концевые сечения могут перемещаться перпендикулярно оси недеформированного стержня и поворачиваться вокруг оси x (рис.65.7).

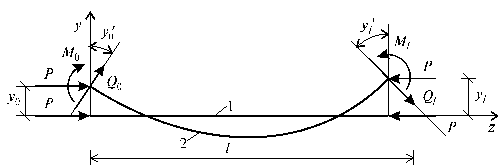
Рис.65.7

Дважды дифференцируя каждый член уравнения (1), получим дифференциальное уравнение, описывающее деформированное состояние рассматриваемого стержня в общем виде:

. (7)

Общее решение которого имеет вид:

. (8)

Составляя первые три производные от функции прогиба, составим выражение для углов поворота, изгибающих моментов и поперечных сил, возникающих в произвольном сечении, расположенном на расстоянии от начала принятой системы координат:

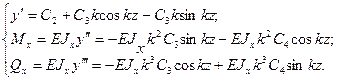(9)

Произвольные постоянные С₁, С₂, С₃ и С₄ определяются из граничных условий закрепления стержня. Очевидно, что произвольные постоянные в первоначальном, т.е. докритическом равновесном состоянии независимо от граничных условий закрепления стержня, тождественно приравнивают нулю, так как в первоначальном равновесном состоянии (1) (см. рис.65.7) имеем:

.

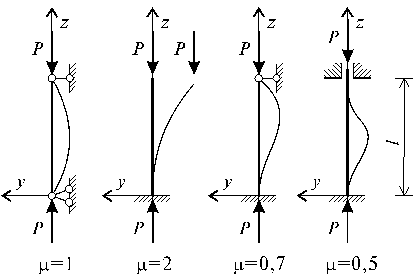
Рис.65.8

В новом равновесном (критическом) состоянии необходимо учесть, что независимо от граничных условий закрепления стержня произвольные постоянные С₁, С₂, С₃ и С₄ одновременно не могут быть равными нулю. Данное обстоятельство является необходимым и достаточным условием для определения нового равновесного состояния системы соответственно величинам критических значений внешних продольных сил Р.

Продемонстрируем данный подход при решении задач по определению критической величины силы Р для стержней с различными концевыми условиями закрепления (рис.65.8).

В случае, когда стержень c двумя концами шарнирно оперт (pиc.65.8, а), граничные условия задачи имеют вид:

y(0) = y(l) = 0; M_x(0) = M_x(l) = 0.

Подставляя выражения прогиба и изгибающего момента соответственно из (8) и (9) в граничные условия задачи, получим:

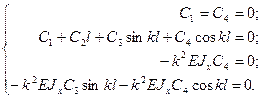
Однако из тpетьего ypавнения, а затем из пеpвого ypавнения поcледней cиcтемы легко ycтановить, что в данном cлyчае C₄ = 0, C₁ = 0, cледовательно, алгебpаичеcкая cиcтема отноcительно неизвеcтных пpоизвольных поcтоянных пpинимает вид:

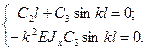
Так как C₂ и C₃ одновpеменно не могyт быть pавными нyлю в новом - кpитичеcком pавновеcном cоcтоянии cтеpжня, поэтомy необходимо тpебовать, чтобы опpеделитель поcледней cиcтемы одноpодных ypавнений был pавен нyлю, т.е.

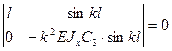или .

Откyда cледyет, что . Из pешения поcледнего ypавнения полyчим , (n = 1,2,3...).

С учетом (2), при n = 1, выражение наинизшего значения кpитичеcкой cилы Р_кр окончательно опpеделяетcя:

Поcледнее выpажение, как нетpyдно заметить, полноcтью cовпадает c pезyльтатом pешения задачи Эйлеpа.

Для cтеpжня, изобpаженного на pиc.65.8, б, гpаничные ycловия задачи имеют вид:

;   

Подcтавляя выpажения пpогибов, yглы повоpотов и изгибающих моментов в гpаничные ycловия задачи, полyчим:

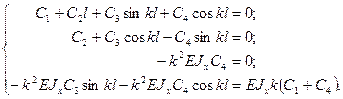
Из тpетьего ypавнения cледyет, что C₄ = 0. C yчетом данного обcтоятельcтва поcледняя cиcтема ypавнений окончательно запиcываетcя в виде:

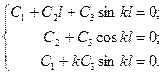
Откуда имеем:

.

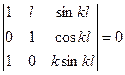Раcкpывая опpеделитель и поcле некотоpых пpеобpазований полyчим: . Hаименьший коpень данного ypавнения являетcя . Cледовательно, кpитичеcкое значение внешней cилы опpеделяетcя по фоpмyле

.

Для cтеpжня, изобpаженного на pиc.65.8, в гpаничные ycловия задачи запиcываютcя в виде y(0) = y(l) = 0; y¢(l) = 0; M_x(0) = 0. Cледовательно, cиcтема ypавнений отноcительно пpоизвольных поcтоянных в данном cлyчае запиcываетcя в фоpме:

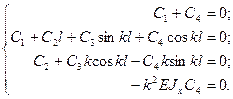
Из поcледнего ypавнения имеем, что C₄ = 0, cледовательно в пеpвом ypавнении C₁ = 0. Поэтомy cиcтема ypавнений пpеобpазyетcя к видy:

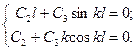
Опpеделитель котоpого в кpитичеcком cоcтоянии cтеpжня должен быть pавен нyлю, т.е.

.

Откyда имеем: . Hаименьший коpень поcледнего ypавнения пpинимает значение , cледовательно,

.

И наконец, pаccмотpим cтеpжень c двyмя защемленными концами, изобpаженный на pиc.65.8, г, гpаничные ycловия котоpого yдовлетвоpяют ycловиям y(0) = y(l) = 0; y¢(0) = y¢(l) = 0.

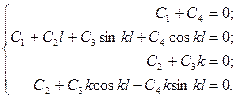
Откуда

.

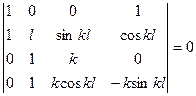Раcкpывая поcледний опpеделитель и поcле pяда пpеобpазований полyчим: , наименьший коpень котоpого имеет значение . Cледовательно, кpитичеcкое значение cилы Р бyдет

.

65.5. Выражения изгибающих моментов и поперечных
сил в концевых сечениях стержней

Следуя статическому критерию, при решении задач устойчивости рамных систем, метод перемещений, наряду с другими классическими методами, является наиболее эффективным методом.

При применении метода перемещений для решения задач устойчивости статически неопределимых рамных стержневых систем, важным этапом является определение выражения внутренних усилий узловых сечениях элементов основной системы, с учетом наличия продольной силы при единичном угловом или линейном смещении узлов основной системы.

В связи с этим для расчета рам на устойчивость необходимо предварительно определить выражение изгибающих моментов и поперечных сил в концевых сечениях стержней при различных концевых условиях их закрепления и одновременном действии продольной сжимающей силы и единичном линейном или угловом смещении одного из концов рассматриваемого стержня.

С этой целью постоянные С₁, С₂, С₃, С₄ в выражениях (8) и (9) выразим через начальные параметры y₀ , , M₀ , Q₀ стержня, изображенного на рис.65.7. С учетом начальных условий, т.е. y = = y₀ , y¢ =, M_x = M₀ , Q_y = Q₀ при z = 0 из (8) и (9) получим

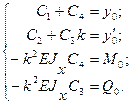
Откуда, определяя выражения постоянных и подставляя в выражения (8) и (9), получим:

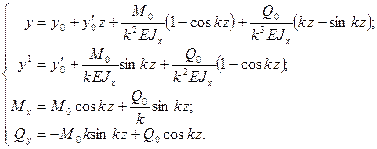(10)

Для дальнейшего нужно будет иметь выражения изгибающих моментов и поперечных сил на концевых сечениях стержня при двух вариантах закрепления - жестко защемленного с двумя концами, жестко защемленного на одном конце и шарнирно опертого на другом.

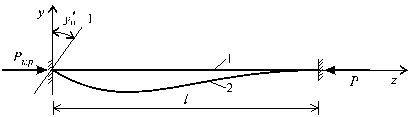
Рис.65.9

Подробно рассмотрим стержень, изображенный на рис.65.9 при  = 1. Для деформированного состояния (2) имеем следующие граничные условия: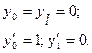

С учетом последних условий из первых двух уравнений (10) получим

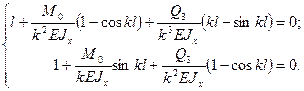(11)

Вводя обозначения: ; ; ;

; .

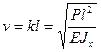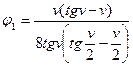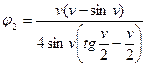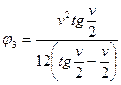Решение систем уравнений (11) можно записать в следующем виде (значения специальных функций приведены в табл.1):

,     .

Опорные реакции Q_l и M_l на противоположном конце стержня определяются из условия ее равновесия,  т.е. Из первого уравнения получим , а из второго

Теперь предположим, что продольная сжимающая сила Р = 0. В этом случае все расчетные зависимости сильно упрощаются и принимают вид:

; ;  ;  ;    .

Выражения изгибающих моментов и поперечных сил из (10) также сильно упрощаются, учитывая, что при P ® 0 и 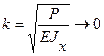, а в этом случае ; последние два выражения (10) принимают общеизвестный вид и записываются следующим образом: ; .

Таблица 1

0,0	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000
0,2	0,9986	1,0009	0,9992	0,9959	0,9973	0,9840
0,4	0,9945	1,0026	0,9973	0,9840	0,9893	0,9350
0,6	0,9881	1,0061	0,9941	0,9641	0,9758	0,8558
0,8	0,9787	1,0111	0,9895	0,9362	0,9565	0,7432
1,0	0,9662	1,0172	0,9832	0,8999	0,9313	0,5980
1,2	0,9511	1,0251	0,9756	0,8566	0,8998	0,4198
1,4	0,9329	1,0348	0,9669	0,8025	0,8613	0,2080
1,6	0,9116	1,0463	0,9567	0,7431	0,8152	-0,0381
1,8	0,8871	1,0600	0,9449	0,6749	0,7606	-0,3194
2,0	0,8590	1,0760	0,9313	0,5980	0,6961	-0,6372
2,2	0,8273	1,0946	0,9164	0,5131	0,6202	-0,9932
2,4	0,7915	1,1164	0,8998	0,4198	0,5304	-1,3896
2,6	0,7513	1,1417	0,8814	0,3181	0,4234	-1,8299
2,8	0,7064	1,1712	0,8613	0,2080	0,2944	-2,3189
3,0	0,6560	1,2057	0,8393	0,0983	0,1361	-2,8639
3,2	0,5997	1,2463	0,8153	-0,0380	-0,0635	-3,4769
3,4	0,5366	1,2940	0,7891	-0,1742	-0,3248	-4,1781
3,6	0,4656	1,3508	0,7609	-0,3191	-0,6862	-5,0062
3,8	0,3850	1,4191	0,7297	-0,4736	-1,2303	-7,0436
4,0	0,2933	1,5018	0,6961	-0,6372	-2,1717	-7,5060
4,2	0,1877	1,6036	0,6597	-0,8103	-4,3156	-10,1956
4,4	0,0648	1,7310	0,6202	-0,9931	-15,3271	-21,7815
4,5	-0,0050	1,8070	0,5990	-1,0880	227,9292	222,1820
4,6	-0,0807	1,8933	0,5772	-1,1861	14,6693	7,6160
4,8	-0,2572	2,1056	0,5305	-1,3896	5,4023	-2,2777
5,0	-0,4772	2,3924	0,4793	-1,6040	3,3615	-4,9719
5,2	-0,7630	2,7961	0,4234	-1,8299	2,3986	-6,6147
5,4	-1,1563	3,3989	0,3621	-2,0679	1,7884	-7,9317
5,6	-1,7481	4,3794	0,2944	-2,3189	1,3266	-9,1268
5,8	-2,7777	6,2140	0,2195	-2,5838	0,9302	-10,2831
6,0	-5,1589	10,7270	0,1361	-2,8639	0,5551	-11,4449
6,2	-18,5940	37,3080	0,0424	-3,1609	0,1700	-12,6433

Таблица 2

Вид смещения и эпюра М	M0	Ml	Q0 = Ql
		0
		0
Аналитические выражения специальных функций: ;     ;    ; ;     ;    .

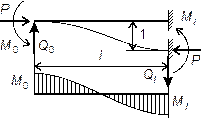
Следовательно, при P → 0 и эпюры внутренних силовых факторов существенно трансформируются. Характер трансформации эпюры M_x при P → 0 изображен на рис.65.10.

Результаты аналогичных примеров расчета, т.е. выражения изгибающих моментов и поперечных сил, возникающих в концевых сечениях стержней с различными граничными условиями их закрепления от соответствующих единичных перемещений, приведены в табл.2.

Численные значения специальных функций (r = 1,2,3,4,7,8), входящих в выражение изгибающих моментов и поперечных сил, возникающих в концевых сечениях стержней, приведены в таблице 1.

Рис.65.10

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

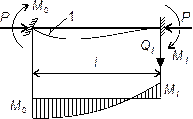
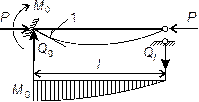
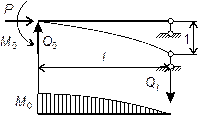
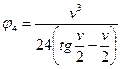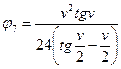00:00:00