Главная
14.4. Свободные
колебания системы с произвольным
числом степеней свободы
Рассмотрим свободные колебания системы с конечным числом степеней свободы. В качестве объекта рассмотрим упругую невесомую балку, изображенную на рис.14.3 и с n сосредоточенными массами m1, m2, m3,..., mn. Пренебрегаем продольными деформациями оси балки в процессе колебаний. При этом положение системы однозначно определяется перемещениями сосредоточенных масс yi (t) (i = 1,2,3,...,n) в произвольные моменты времени t, вызванными упругими деформациями балки в поперечном направлении.
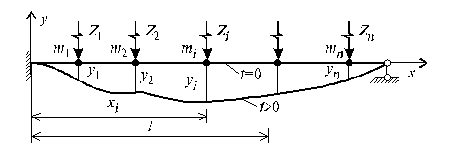
Рис.14.3
Во время движения, пренебрегая
сопротивлением внутренних и внешних сил, на балку будут действовать в качестве
внешних сил инерционные силы 
, (i = 1,2,3,...,n). Применяя
метод сил, перемещение произвольной массы yi (t) записывается в виде суммы:
,
(14.11)
где
- перемещение
i-ой
массы от статической единичной силы, приложенной к k-ой массе от
статической единичной силы по направлению соответствующей инерционной силы.
Подставляя выражение инерционных сил в систему уравнений (14.11), получим:
, (i = 1,2,3,...,n). (14.12)
Система дифференциальных уравнений движения (14.12), описывающая свободные колебания заданной балки, представляет собой замкнутую систему дифференциальных уравнений второго порядка с постоянными коэффициентами, решение которой в общем случае записывается в виде:
.
(14.13)
Рассмотрим одно частное произвольное решение соответствующее r-ой форме колебаний:
. (14.14)
Подставляя (14.14) в (14.12) получим:
,
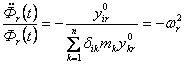(14.15)
которое распадается на две группы уравнений:
(14.16)
и
(14.17)
Решение уравнения (14.16) записывается в виде:
, (r = 1,2,3,...,n). (14.18)
Как видно из (14.18), по произвольной форме r = 1,2,3,...,n колебания
происходят по гармоническому закону с частотой 
. Здесь - частота собственных колебаний заданной системы,
соответствующая r-ой форме.
Согласно (14.14) 
- является
перемещением i-ой массы при r-ой форме колебания, значения которой
определяется из решения системы алгебраических уравнений (14.17).
Система (14.17) относительно (i = 1,2,3,...,n) имеет различные
решения. Очевидно, решение º 0 свидетельствует
об отсутствии движения системы, т.е. состояние покоя системы, которое нас
не интересует.
Система (14.17) может иметь решения, отличные от нулевого лишь в том случае, когда ее определитель равен нулю, т.е. когда выполняется условие:
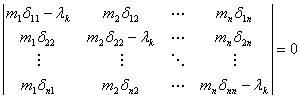, (14.19)
где
принято обозначение 
.
Раскрывая определитель (14.19), получаем
уравнения n-ой степени относительно 
, а при его решении получим n значений . Каждому
значению (r = 1,2,3,...,n) будет
соответствовать своя собственная частота:
,
и свой собственный вектор:
.
При этом собственные формы упругих систем ортогональны между собой:
, (r,k = 1,2,3,...,n; r ¹ k).
(14.20)
Величины
непосредственно из решения (14.17)
определить нельзя, они могут быть найдены с точностью до произвольного
постоянного множителя, т.е. по существу могут быть найдены отношения
между 
. Принимая обозначения 
система (14.17) преобразуется в вид:
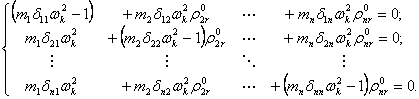
Последняя система имеет одно лишнее
уравнение, так как имеем n уравнений относительно (n-1)
неизвестных 
. Отбрасывая одно из этих уравнений, решая
оставшуюся систему определяют все неизвестные .
Далее, полагая 
, по формуле 
определяются все
остальные амплитуды перемещений масс при r-ой произвольной форме
колебаний.
Возвращаясь к выражению (14.13) с учетом (14.18) можем записать:
(14.21)
Учитывая, что , Ar
и Br
являются произвольными постоянными, решение (14.21) можно записать в более
удобной форме:
и 
можно выразить через
начальные условия каждой массы при t = 0, которыми являются перемещения i-ой массы 
и ее скорости 
, и следовательно, задача о
свободных колебаниях системы с произвольным числом свободы будет полностью
решена.
14.5. Вынужденные
колебания систем с произвольным числом
степеней
свободы при действии вибрационной нагрузки
Рассматриваем
установившиеся вынужденные колебания
системы (рис.14.4) без учета внешнего или внутреннего сопротивления. Будем считать,
что внешнюю нагрузку можно разложить по направлениям перемещений
сосредоточенных масс, а составляющие ее обозначим 
, (i = 1,2,3,...,n).
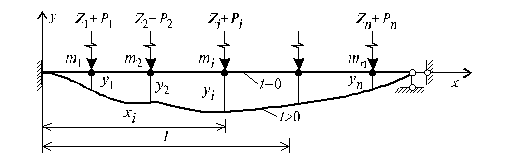
Рис.14.4
Таким образом, роль внешних сил здесь будут играть величины:
.
(14.22)
Канонические уравнения метода сил в данном случае записываются в виде:
(r = 1,2,3,...,n). (14.23)
Подставляя (14.22) в (14.23) и после ряда преобразований, получим:
(i = 1,2,3,...,n).
(14.24)
Здесь
- амплитудное
значение перемещения i-ой массы, вызванное действием системы внешних сил 
.
Частное решение системы уравнений (14.24) записывается в виде:
,
(14.25)
где
- амплитуда
перемещения i-ой массы; 
- частота вынужденных колебаний системы.
Выражение для определения инерционных сил принимает вид:
Zi (t) = 
,
(14.26)
где 
- амплитудные
величины инерционных сил.
Принимая обозначение
(14.27)
и с учетом (14.26) систему уравнений можно преобразовать к следующему виду:
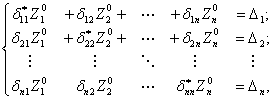(14.28)
решение которого записывается в виде:
.
(14.29)
Здесь D
и Di
- соответственно,
определитель системы (14.28) и определитель, полученный из D заменой элементов (k = 1,2,..., n) соответствующими свободными членами 
(i = 1,2,..., n), т.е.
;
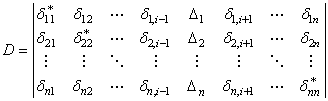. (14.30)
Нетрудно заметить, что определитель D совпадает по форме с выражением
(14.19), и поэтому при 
, т.е. при стремлении значения частоты вынужденных колебаний
к частоте собственных колебаний заданной системы, получим 
, следовательно 
и соответственно, и
согласно (14.26) 
, т.е. будет иметь место резонанс.
График зависимости 
от частоты имеет вид, приведенный на рис.14.5.
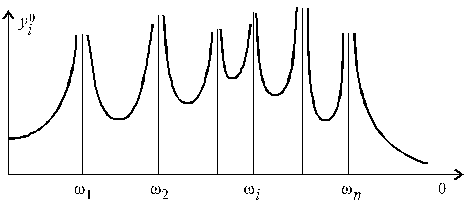
Рис.14.5
Однако увеличение амплитуды колебаний при
резонансе до бесконечности является абстракцией. В действительности всегда
имеются контуры, ограничивающие величину амплитуды , в частности внутреннее трение материала конструкции или
внешнее сопротивление. Поэтому в действительности при происходит
значительное увеличение , при этом оставаясь конечной величиной.
После определения 
из (14.29) с учетом (14.22) следует определить
амплитудное значение внешних сил:
, (i = 1, 2,..., n),
(14.31)
и
по значениям 
(i = 1, 2,..., n) определить
амплитудное значение внутренних усилий.
Например, общее выражение для определения амплитудных значений изгибающих моментов от динамических сил Ri (t) для статически неопределимых систем можно записать в виде:
,
где
Mik (k,i = 1,2,..., n) - значение момента в i-ом сечении при действии единичной силы 
в точке k.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Теория машин и механизмов
