Главная
14.6.
Пример динамического расчета рамы
На раме с размерами, указанными на рис.14.6, в точках 1 и 2 установлены два одинаковых вибратора весом G = 20 кН каждый и весом неуравновешенных частей Р0 =1,2 кН, размещенные на оси вращения с эксцентриситетом е = 0,015 м. Вибраторы вращаются синфазно с частотой n = 600 об/мин.
Рама выполнена из двух двутавров № 50 (ГОСТ 8239-72), т.е. Jx = 3,29×10-4 м4; Wx =0,157×10-2 м3. Рама изготовлена из стали с характеристиками Е = 2,1×105 МПа, R = 190 МПа.
Пренебрегая собственным весом рамы и внутренним трением материала, требуется:
1. Составить канонические уравнения по методу сил, определяющие свободные колебания рамы, и получить значения частот и периодов собственных колебаний рамы;
2. Вычислить отношения амплитуд и графически изобразить возможные формы собственных колебаний рамы;
3. Проверить ортогональность собственных форм колебаний системы;
4. Определить круговую частоту вынужденных колебаний и изобразить примерный вид графика коэффициента динамичности;
5. Составить канонические уравнения по методу сил, определяющие вынужденные колебания системы, и определить амплитудные значения инерционных сил;
6. Построить статическую эпюру изгибающих моментов от всех вибраторов и эпюру амплитудных значений изгибающих моментов при вынужденном режиме колебания рамы;
7. Построить эпюру моментов при одновременном действии статических и динамических сил и определить положение опасного сечения конструкции;
8. Вычислить максимальное значение напряжения в опасном сечении и проверить условия прочности для принятого поперечного сечения рамы.
Решение:
Расчетная схема рассматриваемой системы показана на рис.14.6. Под действием периодической возмущающей нагрузки рама совершает колебательное движение.
Рис.14.6
Пренебрегая внутренним трением материала рамы и ее собственным весом, упругие перемещения сечений 1 и 2 по принципу независимости действия сил записываются в виде:
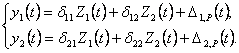(14.32)
где
- перемещение
i-ого сечения от статической единичной силы, приложенной в k-ом сечении (i = 1,2; k = 1,2) по направлению
соответствующей инерционной силы; 
, 
- перемещения
сечений 1 и 2 от всех динамических нагрузок. При этом:
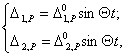(14.33)
где
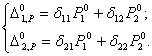(14.34)
С учетом выражений (14.33) и (14.34) и m1 = m2 = m уравнение (14.32) в стационарном режиме колебаний можно переписать в виде:
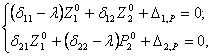(14.35)
где 
.
Решая систему уравнений (14.35) определяют амплитудные значения инерционных нагрузок (способом Крамера):
, (i = 1,2), (14.36)
где приняты следующие обозначения:
.
Учитывая, что в данном случае P1 = P2, амплитуды динамического прогиба и изгибающего момента в произвольном i-ом (i = 1,2,...) сечении могут быть определены по формулам:
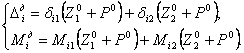(14.37)
Уравнения движения (14.32) при свободных колебаниях рамы, т.е. при P1 = P2 = 0, принимают вид
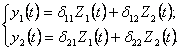(14.38)
Относительно амплитуды перемещения последняя система уравнений преобразуется в виде:
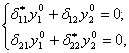(14.39)
где
.
Здесь 
- частота
собственных колебаний рамы.
Система алгебраических уравнений (14.39)
относительно амплитуды перемещения сосредоточенных масс имеет различные решения.
Очевидное решение 
свидетельствует об
отсутствии движения системы и не подходит по смыслу поставленной задачи.
Система (14.39) может иметь решения, отличные от нулевого, лишь в том случае, когда ее определитель равен нулю, т.е. когда выполняется условие:
.
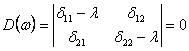(14.40)
Раскрыв определитель (14.40), получим
квадратное уравнение относительно 
. После определения с учетом (14.39)
вычисляются собственные частоты 
.
Первая частота 
называется частотой
основного тона собственных колебаний. Каждой частоте соответствует
определенная форма колебаний системы. Форму колебания можно изобразить
графически. Для этого в уравнения (14.39) следует подставить значение 
(i = 1,
2), причем:
. (14.41)
При этом одно из двух уравнений (14.39) становится лишним. Пренебрегая первым уравнением (14.39), из второго получим:
, (i = 1,2).
(14.42)
После чего, задавая значение yii (i = 1,2), можно
вычислить 
в долях
, а 
- в
долях 
и изобразить
графический характер возможной формы колебаний первого и второго тона
колебаний.
Формы колебаний должны быть ортогональны. Условие ортогональности собственных форм записывается в виде:
, (r,k = 1,2; r ¹ k).
(14.43)
Определив собственные частоты и 
и
вычислив частоту вынужденных колебаний 
, необходимо сопоставить с ближайшей из или . Во избежание наступления резонансных колебаний
рекомендуется, чтобы отличалась от любой из
частот , не менее чем на
30%. Если при решении задачи окажется, что это требование не выполняется, то
следует изменить значение 
или . Этого можно
достичь путем:
- изменения геометрических или физико-механических характеристик материалов элементов рамы;
- уменьшения или увеличения частоты вращения вибратора.
При этом во всех случаях напряжения в опасных сечениях рамы должны удовлетворять условиям прочности.
Переходим к численной реализации решения в соответствии с постановкой задачи.
1. Определение частот и периодов собственных колебаний рассматриваемой системы
Предварительно определим изгибную жесткость элементов заданной системы:
кН×м2.
Заданная система один раз статически неопределима. Основная система метода сил представлена на рис.14.7, а. Эпюра моментов в основной системе от действия силы Х1 = 1 показана на рис.14.7, б, а от единичных внешних сил - на рис.14.8, а, б.
Сначала рассчитываем раму на действие силы 
. Каноническое уравнение метода сил в данном случае
записывается в виде:
.
(14.44)
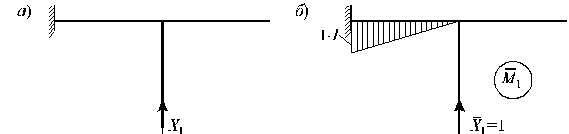
Рис.14.7
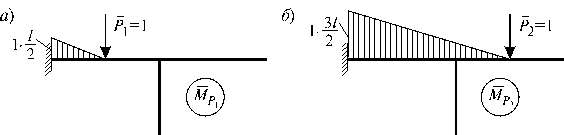
Рис.14.8
Коэффициенты 
и 
находим перемножением
эпюр 
и 
по формуле Мора.
Здесь 
определяется как
результат перемножения эпюры (рис.14.7, б) самой на себя, как результат перемножения эпюры (рис.14.7, б) с (рис.14.8, а).
(14.45)
С учетом (14.45) из решения (14.44) получим:
.
Эпюра изгибающих моментов в заданной системе от действия сил Р1 =1 и Х1 = 5/16 изображена на рис.14.9, a.
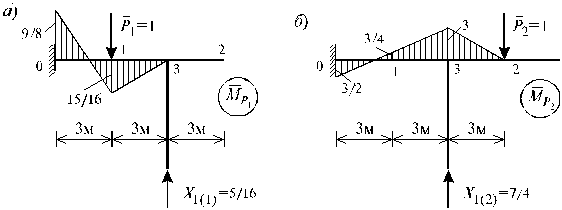
Рис.14.9
Рассчитываем раму на действие силы Р2 = 1. Каноническое уравнение метода сил в данном случае принимает вид:
.
(14.46)
Здесь 
определяется как
результат перемножения эпюры моментов, изображенных на рис.14.7, б и 14.8, б, в соответствии с формулой Мора:
.
(14.47)
С учетом значения из (14.45) и значения из (14.47) и из
(14.46) получим:
.
Эпюра изгибающих моментов от действия сил Р2 = 1 и Х1 = = 7/4 в заданной системе изображена на рис.14.9, б.
Единичное перемещение 
определяется по
формуле Мора в результате перемножения эпюры 
самой на себя,
применяя формулы умножения двух эпюр моментов в виде двух трапеций на
произвольном участке. Получим:
м/кН.
Единичное перемещение 
определяется по
формуле Мора перемножением эпюры 
самой на себя
(рис.14.9, б):
м/кН.
Единичное перемещение 
определяется по
формуле Мора в результате перемножения эпюр и , изображенных соответственно на рис.14.9, а, б:
м/кН.
Решив уравнение (14.40), получим:
,
откуда
.
Окончательно 
=166,75×10-6 м/кН; 
=10,.35×10-6 м/кН.
По формуле (14.41) определяется значение собственной частоты рассматриваемой рамы:
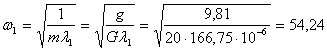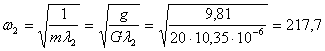c-1;
c-1.
Периоды
собственных колебаний рассматриваемой системы принимают значения: 
c; 
c.
2. Определение
амплитуды собственных колебаний и графическое изображение собственных форм
Для вычисления значения отношений амплитуды
собственных колебаний из (14.42), предварительно определив 
кН∙с2/м, имеем при 
= 1 и при 
= 1, соответственно:
Формы собственных колебаний рассматриваемой системы изображены на рис.14.10 (а - первая форма; б - вторая форма).
3. Проверка
ортогональности собственных форм колебаний
Из условия ортогональности (14.43) имеем:
.
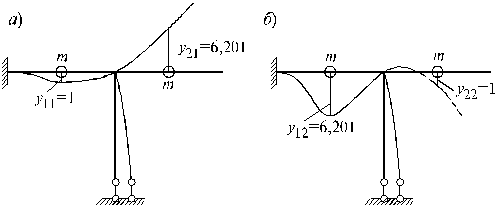
Рис.14.10
4. Определение
круговой частоты вынужденных колебаний и изображение примерного вида графика
коэффициента динамичности в зависимости от отношения частот вынужденных и
собственных колебаний
В стационарном режиме круговая частота вынужденных колебаний системы имеет значение:
c-1.
Сопоставим величину с величиной ближайшей
собственной частоты рамы :
.
Во избежание резонансных колебаний надо
изменить величину или . В данном случае, принимая n = 900 об/мин,
получим:
c-1;
,
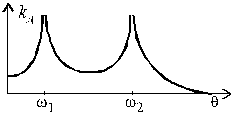
Рис.14.11
Следовательно, при 
с-1 принятое условие во избежание
резонансных колебаний выполняется.
Примерный вид графика коэффициента
динамичности в зависимости от 
изображен на рис.
14.11.
5. Определение амплитудных значений инерционных сил
В соответствии с принятым обозначением по формулам (14.34) и (14.35) последовательно определяем:
м/кН;
м/кН;
кН;
м/кН;
м/кН;
м2/кН;
м2/кН;
м2/кН.
По (14.33) определяем амплитудные значения инерционных сил:
= |D1/D |= |3,72/0.5| =
7,44 кН;
= |D2/D |= |9,64/0.5 |=
19,28 кН.
6. Определение
эпюры изгибающих моментов от действия собственного веса вибраторов и
амплитудных значений изгибающих моментов при вынужденном стационарном режиме
колебания рамы
Значение изгибающих моментов, возникающих от действия собственного веса вибраторов, в произвольном сечении определяется по формуле:
.
Определяем значение 
в характерных сечениях
(0; 1; 2; 3) рамы (см. рис.14.9):
сечение 0: 
= 20×(9/8 - 3/2)
= -7,5 кН×м;
сечение 1: 
= 20×(-15/16 + 3/4) = -3,75 кН×м;
сечение 2: 
= 0;
сечение 3: 
= 20×(0 +
3) = 60 кН×м.
Эпюра изгибающих моментов приведена на
рис.14.12.
Амплитудные значения изгибающих моментов от действия внешних динамических и инерционных нагрузок в соответствии с (14.37) определяются:
= 
.
Рис. 14.12
Согласно последней формуле 
в характерных сечениях
имеет
следующие значения:
сечение 0: 
кН×м;
сечение 1: 
кН×м;
сечение
2: 
= 0;
сечение 3: 
кН×м.
Эпюра изображена на
рис.14.12 (пунктиром).
7. Построить
эпюру моментов при одновременном действии статических и динамических сил и
определить положение опасного сечения конструкции
Результирующее значение изгибающих моментов, действующих в характерных сечениях при одновременном действии статических и динамических нагрузок, определяется по формуле:
.
Эпюра Mk, как и эпюры и , изображены на рис.14.12.
Из рис.14.12 согласно эпюре М следует, что наиболее опасным является сечение 3.
8. Определение
максимального напряжения и проверка условий прочности в наиболее опасном
сечении
кН/м2 = 53,2МПа <R = 190 МПа.
Следовательно, условие прочности рассматриваемой рамы обеспечено.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Теория машин и механизмов
