Главная
Часть
15. Изгиб и кручение тонкостенных стержней
15.1.
Общие положения и основные особенности расчета
В настоящее время в машиностроении, авиации, строительстве, железнодорожном транспорте все больше используются конструкции, выполненные из тонкостенных и штампованных профилей или просто из тонколистовой стали. Эти конструкции обеспечивают высокую жесткость и прочность при сравнительно небольшом весе, поэтому их применение в технике является весьма экономичным. На железнодорожном транспорте это элементы тележек, стенок локомотивов, вагонов и многих других конструкций.
Специфика расчета этих конструкций на прочность породила особую расчетную схему - схему тонкостенного стержня.
Основным признаком тонкостенного стержня является характерное отношение его геометрических размеров. В поперечном сечении одно из измерений (толщина) существенно меньше другого- срединной длины контура s. Последняя в свою очередь намного меньше, чем длина стержня l (рис.15.1).
Длина контура для тонкостенного стержня, представленного на рис.15.1:
s = h + 2b.
Следовательно, характерные размеры тонкостенных стержней открытого профиля
взаимосвязаны и меняются в пределах 
и 
.
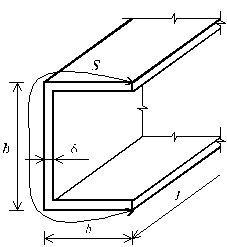
Рис. 15.1
Основные положения теории тонкостенных стержней были даны С.П. Тимошенко. Полное и общее развитие эта теория получила в трудах В.З. Власова и потому обычно называется теорией Власова.
Тонкостенный стержень, как расчетная схема, сохраняет в себе основные свойства обыкновенного стержня и формулы сопротивления материалов, связанные с растяжением (сжатием), изгибом и кручением бруса, остаются в основном справедливыми.
Вместе с тем, тонкостенный стержень в силу геометрических соотношений обнаруживает свойства, существенно отличающие его от стержней сплошного сечения. При некоторых видах загружения не соблюдается гипотеза плоских сечений, происходит так называемая депланация сечения за счет неравномерной деформации стержня вдоль его оси. Иными словами, не соблюдается принцип Сен-Венана - глубина «проникновения» краевых особенностей вдоль оси существенно больше, чем в сплошном стержне.
Вообще говоря, сравнительная оценка нормальных и касательных напряжений s и t в поперечных сечениях бруса при переходе от сплошного сечения к тонкостенному профилю существенно меняется, и этот вопрос требует особого изучения.
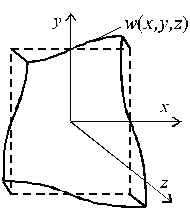
Рис.15.2
При кручении тонкостенных стержней и вообще стержней с некруглым поперечным сплошным сечением, поперечные сечения плоские до деформации, искривляются по некоторой поверхности w(x, y, z) (рис.15.2), что называется депланацией сечения. По характеру формирования депланаций сечения по длине стержня, следует различать два типа кручения стержней: свободное и стесненное.
Если депланация во всех поперечных сечениях одинакова по длине стержня или иначе w(x, y, z) = w(x, y), т.е. она является постоянной и не зависит от z, то такое кручение называется свободным. При переменных депланациях по длине стержня, кручение называется стесненным.
При свободном кручении в поперечных сечениях стержня возникают только касательные напряжения, а при стесненном кручении, наряду с касательными возникают и нормальные напряжения. Эффект от неравномерной депланации сечения по его длине наиболее существенен для стержней открытого профиля.
После определения полной системы внешних сил, заметим, что порядок вычисления напряжений и перемещений в тонкостенном стержне закрытого профиля при свободном кручении принципиально ничем не отличается от метода расчета обычных стержней. Поэтому, здесь этому вопросу специальное внимание не уделяется.
15.2. Секториальная площадь
В дополнение к уже известным геометрическим характеристикам сечений (F - площадь поперечного сечения; Sx, Sv - статические моменты сечения; Jx, Jv, Jxy - осевые и центробежный моменты инерции) введем ряд новых. Эти характеристики свойственны только тонкостенным стержням и определяются на основе понятия секториальной площади.
Рассмотрим срединную линию контура
поперечного сечения (рис.15.3). Срединная
линия - это
геометрическое место точек поперечного сечения, равноудаленно
расположенных от контурных линий. Выберем на срединной линии начало 0
отсчета дуги s и из заданного полюса Р. Проведем два луча к концам
элементарного отрезка ds.
Удвоенную площадь треугольника PAB
обозначают через 
.
Очевидно, что
, (15.1)
где r - расстояние от полюса Р до касательной к линии контура в точке А.
Интеграл
,
(15.2)
называется
секториальной площадью. Таким образом, секториальная площадь представляет собой удвоенную
площадь, очерчиваемую радиус-вектором РА при движении т. А по контуру от начала отсчета 0 до
некоторого значения дуги s. Если радиус-вектор вращается по часовой стрелке, приращение площади
имеет знак плюс,
против часовой стрелки -
минус.
Рис.15.3
Точка Р называется секториальным полюсом.
При заданном полюсе и заданном начале отсчета в каждом конкретном случае может быть построена эпюра секториальной площади.
Рис.15.4
В качестве примера построим эпюру секториальной площади для контура, приведенного на рис.15.4, а. Выбираем в качестве полюса точку P, а за начало отсчета принимаем точку 0 (рис.15.4, а).
Рассмотрим участок 0-3. На этом участке 0 £ s £ a. Вектор r вращается по часовой стрелке, следовательно эпюра 
имеет знак плюс:
; 
; 
.
На участке 3-4, 0 £ s £ a, вектор r вращается против часовой стрелки, то есть приращение площади будет отрицательным:
; ; 
.
На участке 0-2, 0 £ s £ a, вектор r вращается против часовой стрелки, то есть приращение площади будет отрицательным:
; ; 
.
На участке 2-1, 0 £ s £ a, вектор r вращается по часовой стрелке, то есть приращение площади будет положительным:
; ; 
.
Эпюра секториальной
площади приведена на
рис.15.4, б.
Отметим, что при переносе полюса секториальная площадь меняется на величины, линейно зависящие от координат x и y, т.е.:
,
(15.3)
где
и 
- секториальная площадь относительно нового Р0 и старого полюса Р', соответственно; xc, yc, x0, y0 - координаты
центра изгиба и начала отсчета, соответственно.
15.3. Секториальные характеристики и их определение
Наряду с общепринятыми, для тонкостенных стержней вводятся дополнительные характеристики поперечных сечений.
Секториально статический момент поперечного сечения:
, м4 .
Секториально
линейные моменты площади поперечного сечения:
и 
, м5 .
Секториальный момент инерции поперечного сечения:
, м6 .
Окончательные выражения секториальных характеристик, исходя из предположения, что толщина тонкостенного сечения по всему контуру постоянна и равна d.
При поперечном изгибе или кручении всегда существует такая точка, относительно которой момент от касательных сил, возникающих в поперечном сечении, равен нулю. Эта точка называется центром изгиба или кручения. Для сечений, имеющих две оси симметрии, центр изгиба или центр кручения совпадают с центром тяжести.
Положение центра изгиба (или кручения) не зависит от действующих на стержень сил, а зависит только от формы и размеров поперечного сечения тонкостенного стержня.
При стесненном кручении центр кручения, а также начало отсчета секториальной площади не могут быть выбраны произвольно. Эти точки должны быть выбраны так, чтобы секториально линейные моменты, а также секториально статический момент были равны нулю, т.е.:
(15.4)
Выполнение условий первых двух условий из (15.4) зависит только от выбора координат полюса. Выполнение же третьего из условий (15.4) зависит от выбора начала отсчета 0.
Эпюра , построенная при полюсе, в качестве которого взят центр
изгиба, и удовлетворяющая третьему уравнению (15.4), носит название эпюры главной сектроиальной
площади.
Положение центра изгиба и секториальные характеристики сечения на практике определяются в следующей последовательности.
Сначала выбирается положение полюса Р и строится эпюра
секториальной площади ¢
относительно полюса.
Далее определяются величины 
и 
относительно полюса P и вычисляются координаты центра изгиба
по формулам:
и 
. (15.5)
Определяется секториальная площадь относительно центра изгиба по формуле (15.3) и вычисляется секториaльно стaтический момент поперечного сечения по формуле:
,
как
площадь эпюры 
, умноженную на 
.
Далее определяется постоянная D из третьего условия (15.4) по формуле:
(15.6)
и строится эпюра главной секториальной площади:
.
(15.7)
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Теория машин и механизмов
