Главная

15.5. Расчет тонкостенного стержня открытого профиля

Для тонкостенного стержня открытого профиля, изображенного на рис.15.8, а, при следующих исходных данных: H = 12,5×10^-2 м; B = 19×10^-2 м; l = 2 м; = 1×10^-2 м; P = 1 кН; E  = 2×10⁵ МПа; G = 8×10⁴ МПа, требуется:

1. Определить площадь, положение центра тяжести, главные центральные моменты инерции поперечного сечения;

2. Найти положение центра изгиба;

3. Определить момент инерции при чистом кручении J_кр и секториальные характеристики сечения;

4. Вычислить изгибно-крутильную характеристику ;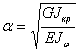

5. Построить эпюры поперечной силы Q_x, изгибающего момента M_y, момента чистого кручения M_z, изгибно-крутящего момента M_w, бимомента B_w;

6. Построить эпюры нормальных напряжений s_z, s_w и их суммарную эпюру.

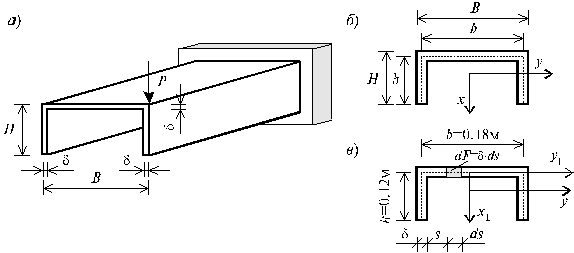
Рис.15.8

Решение:

1. Определение площади, положения центра тяжести и главных центральных моментов инерции

Вычислим расчетные размеры сечения стержня (рис.15.8, б, в), приняв в дальнейших расчетах:

м = const; м;

м.

Тогда

м².

В выбранной системе координат x₁y₁, определим положение центра тяжести сечения: y_c = 0;

Для этого построим эпюру координат x₁ (рис.15.9, а) и вычислим статический момент сечения относительно оси y₁:

м³.

Тогда координата центра тяжести сечения будет равна:

м.

Для вычисления главных центральных моментов инерции предварительно построим эпюру координат x и y (рис.15.9, б, в). С применением этих эпюр, определяются:

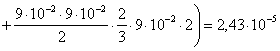м⁴;

м⁴.

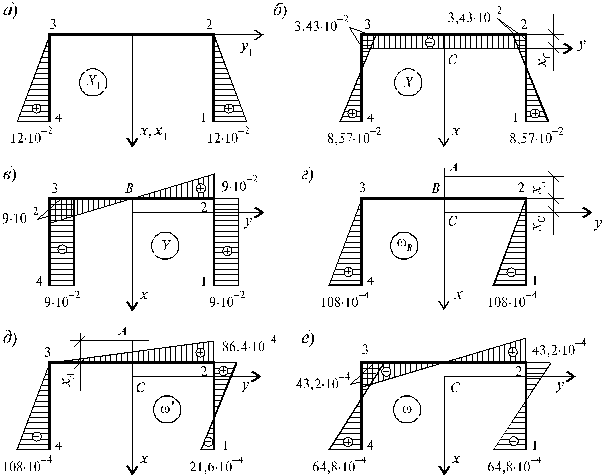
Рис.15.9

2. Определение положения центра изгиба

Вначале построим эпюру секториальных координат площади , в характерных точках (1, 2, 3, 4) профиля, выбрав произвольный полюс в точке B (рис.15.9, г):

м²;

;

м².

Координаты центра изгиба вычисляем по формулам (15.5).

Используя эпюры и y и применяя правило Верещагина, вычисляем секториально линейный статический момент:

= -116,64×10^-8 м⁵.

Тогда координата центра изгиба по вертикальной оси принимает значение:

м.

Координата центра изгиба по горизонтальной оси вычисляется

Так как эпюра x симметрична, а эпюра обратно симметрична относительно x, то по правилу Верещагина секториально-линейный статический момент равен нулю, т.е.:

.

Cледовательно, y_А = 0 и поэтому центр изгиба лежит на оси x.

Вычислим постоянную D, предварительно построив эпюру секториальных площадей ' (рис.15.9, д).

При этом полюс расположим в центре изгиба (т. А). За начало отсчета возьмем точку 3 (произвольно):

м²;

м²;

м².

Постоянную D вычисляется по формуле (15.6):

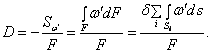
Далее вычисляем секториально статический момент , как произведение площади эпюры ' на d :

м⁴ .

В этом случае величина постоянной D будет равна:

м² .

Далее, используя зависимость (15.7), вычисляем секториальные координаты характерных точек профиля:

м^{2 ;}

м^{2 ;}

м^{2 ;}

м² .

По полученным координатам строим эпюру (рис.15.9, е).

3. Определить момент инерции при чистом кручении и секториальные характеристики сечения

Для корытообразного профиля поперечного сечения бруса (рис. 15.8, б), имеем:

м⁴ .

Cекториальный момент инерции J_w вычисляем по эпюре (рис.15.9, е):

»м⁶ .

4. Определение изгибно-крутильной характеристики 

Изгибно-крутильную характеристику вычисляем по формуле:

м^-1 .

5. Построение эпюр поперечной силы Q_x , изгибающего момента M_y , момента чистого кручения M_z , изгибно-крутящего момента М_w и бимомента В_w

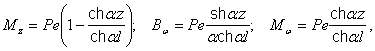
В рассматриваемом примере:

м;    кН = 95 Н;

;  ch= 6,7690;  × ch= 1,3×6,7690 = 8,7997 м^-1.

Тогда, согласно (15.25), получим:

Предварительно разбив тонкостенный брус по длине на 5 равных частей, для этих сечений численные значения величин Q_x , M_y , M_g , М_w и В_w приведены в таблице 15.2.

По результатам табл. 15.2 строим эпюры Q_x , M_y , M_g , М_w и В_w (рис.15.10). При этом в случае действия на брус сосредоточенной силы, во всех сечениях выполняется следующее условие: .

Таблица 15.2

z, м		sh	ch	Qx, Н	My, Н×м	Mz, Н×м	Мw, Н×м	Вw, Н×м2
0,00	0,00	0,0000	1,0000	1000	0	80,97	14,03	0
0,40	0,52	0,5438	1,1383	1000	400	79,03	15,97	5,87
0,80	1,04	1,2379	1,5913	1000	500	72,67	22,33	13,37
1,20	1,56	2,2743	2,4845	1000	1200	60,14	34,86	24,50
1,60	2,08	3,9398	4,0647	1000	1600	37,96	57,04	42,56
2,00	2,60	6,6947	6,7690	1000	2000	0,00	95,01	72,32

6. Построить эпюры нормальных напряжений s_z, s_w и их суммарную эпюру

Нормальные напряжения зависят от внутренних силовых факторов M_y и В_w согласно выражения (15.11). Опасным сечением является сечение в заделке, так как в нем действуют наибольшие по величине M_y и В_w (рис.15.10, в, д). Нормальные напряжения от изгиба (рис.15.11, а) определяем по формуле:

Па = -303,8 x₁ МПа.

В точке 1: x₁ = 8,57×10^-2 м, = -303,8×8,57×10^-2= -26 Мпа.

В точке 2: x₁ = -3,43×10^-2 м, = -303,8×(-3,43×10^-2) = 11,94 МПа.

В точке 3: x₁ = -3,43×10^-2 м, = -303,8×(-3,43×10^-2) = 11,94 МПа.

В точке 4: x₁ = 8,57×10^-2 м, = -303,8×8,57×10^-2= -26 МПа.

По найденным данным строим эпюру s_z (рис.15.11, а).

Рис.15.10 Рис.15.11

Нормальные напряжения в точках профиля от действия бимомента В_w вычисляем по формуле:

Па = МПа.

В точке 1: МПа.

В точке 2: МПа.

В точке 3: МПа.

В точке 4: МПа.

По полученным данным строим эпюру . Суммарные нормальные напряжения в опасном сечении тонкостенного стержня от совместного действия изгиба и стесненного кручения вычислим путем сложения эпюр и по формуле: .

В точке 1: = -26 - 1,55 = -38,55 МПа.

В точке 2: = 11,94 + 8,37 = 20,31 МПа.

В точке 3: = 11,94 - 8,37 = 3,57 МПа.

В точке 4: = -26 + 12,55 = -13,45 МПа.

Суммарная эпюра нормальных напряжений приведена на рис.15.11, в.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00