Главная

Часть 17. Основы теории пластичности и ползучести

17.1. Основы деформационной теории пластичности

Для изучения работы конструкций за пределами упругости необходимо предварительно сформулировать критерии перехода от упругого к упруго-пластическому состоянию и сформулировать новые физические уравнения взамен закона Гука, который как известно, справедлив только для описания связи между напряжениями и деформациями только упругой стадии работы конструкции.

Для сложного напряженного состояния имеем линейные соотношения обобщенного закона Гука:

Условия перехода из упругого состояния в упруго-пластические могут быть определены по формулам одной из гипотез предельного состояния.

Для выполнении практических расчетов наибольшее распространение нашла гипотеза энергии формоизменения, согласно которому переход из упругого состояния в пластическое происходит когда интенсивность напряжений , достигает предела текучести, т.е.:

где - интенсивность напряжений определяется через компоненты тензора напряжений:

или через главные напряжения

Для упругого состояния как известно взамен (17.1) справедливо и следующее обобщенное соотношение:

где Е - является модулем упругости материалов и определяется из диаграммы при одноосных испытаниях материалов (рис.17.1), как , а - интенсивность деформаций:

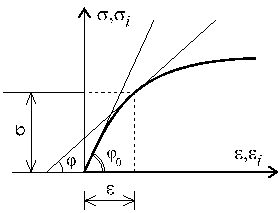
Рис.17.1

Соотношение (17.3) можно трактовать как одну из форм выражения закона Гука.

Анализ многочисленных экспериментальных данных показывают, что в упруго-пластическом состоянии связь между интенсивностью напряжений и деформацией можно записать в следующем виде:

где - является переменная величина, и определяется из диаграммы при одноосных испытаниях материалов (рис.17.1.). При этом Таким образом, соотношение (17.4) устанавливает положение в том, что свойства материала не зависит от вида напряженного состояния. Это положение является исходным в деформационной теории пластичности.

Вторым положением, на котором базируется деформационная теория пластичности, является условие, что изменение объема:

остается чисто упругим. Это положение также хорошо согласуется с экспериментальными данными.

Далее учитывая, что е является величиной порядка упругих удлинений, то можно исходить из того, что при пластическом деформировании объем меняется незначительно. Поэтому в пластическом состоянии коэффициент Пуассона допускается принимать равным .

Из выражения (17.4) для модуля деформации можно представить в следующем виде:

Согласно первому положению деформационной теории пластичности зависимость между напряжениями и деформациями при одноосном сжатии и растяжении едины для всех видов напряженных состояний. Поэтому, диаграмма между и идентична диаграмме и . Следовательно (17.5) можно представить в виде:

Аналог модуля сдвига определяется:

Физические соотношения между напряжениями и деформациями, аналогично (17.1), для пластичного состояния тела принимает вид:

Приведенные физические соотношения являются приближенными и считаются справедливыми только для тех видов нагружения, при которых внешние силы в процессе нагружения возрастают прямо пропорционально по времени.

В этом случае, главные оси напряженного состояния при изменении внешних сил сохраняют свое направление, т.е. соотношение (17.7) справедливо только при простом нагружении.

17.2. Упруго-пластический расчет стержня при

действии продольной силы

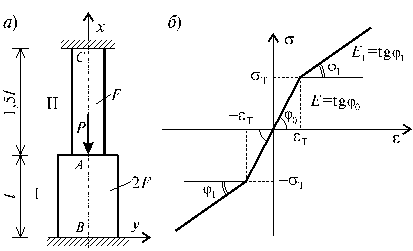
Рис.17.2

Определить перемещение сечения А ступенчатого стержня изображенного на рис.17.2, а при различных стадиях его деформирования при нагружении его силой Р. Диаграмма деформирования изображена на рис.17.2, б.

Решение:

В данном случае все составляющие тензора напряжений и деформаций за исключением s_х и e_х тождественно равны нулю. При этом участок АС испытывает растяжения, а участок АВ - сжатие.

Следует выделить следующие этапы работы конструкций.

На первом этапе, участки АС и АВ деформируются в упругой стадии, т.е.:

при

На втором этапе, один из участков АВ или АС переходит в упруго-пластическую стадию деформирования. И, наконец, когда оба участка АВ и АС деформируются в упруго-пластической стадии.

Связь между и в упруго-пластической стадии деформирования согласно диаграмме записывается в виде:

при

На первом этапе нагружения, когда в обоих участках материал конструкции деформируется по закону Гука, учитывая, что система один раз статически неопределима усилия N обоих участков определяется обычными приемами. Из условий равновесия имеем:

-N₁ + N₂ = P. (17.10)

Учитывая, что стержни верхним и нижним концами жестко закреплены, его абсолютное удлинение должно быть равно нулю, т.е.:

откуда

В результате совместного рассмотрения (17.10) и (17.11) получим:

Перемещение сечения А будет следующим:

В упругой стадии работы конструкции значения напряжения на первом и втором участках соответственно принимают значения:

Так как то соотношения (17.1217.14) будут справедливы до тех пор, пока напряжения на первом участке не достигнет значения .

Из выражения (17.14), принимая , определяем величину силы Р, при которой нижний участок с номером I переходит в пластичное состояние, а верхний участок с номером II остается упругим:

Для второго этапа нагружения, необходимо преобразовать уравнения совместности деформаций:

Выражение (17.9) представим в виде:

Тогда

Подставляя (17.18) в (17.16) получим:

Совместно решая (17.19) с уравнением равновесия (17.10) получим:

Принимая в (17.20) Е = Е₁, можно убедиться, что из (17.20) следуют упругие решения (17.14).

Перемещая сечения А на данном этапе нагружения определяется по формуле:

Переходим к решению поставленной задачи на третьем этапе нагружения. Принимая из второго выражения (17.14) определим значения внешней силы при которой второй участок переходит в пластическую стадию деформирования:

На третьем этапе нагружения, т.е. абсолютное удлинение второго участка определяется:

Подставляя (17.23) и (17.18) в (17.16) получим:

В результате совместного рассмотрения (17.24) и (17.10) определяется:

Принимая Е = Е₁ из (17.25) получим решение задачи в упругой постановке, которая полностью согласуется выражением (17.12). Перемещение сечения А на третьем этапе нагружения определяется по выражению:

Если в последнем варианте предположить Е = Е₁, то отсюда следует решение в упругой постановке задачи, и полностью совпадающей с решением (17.13).

17.3. Упруго-пластический изгиб бруса

Рассмотрим упруго-пластический чистый изгиб бруса. Для простоты предполагается, что поперечное сечение бруса обладает двумя осями симметрии (рис.17.3, а) и что диаграмма деформирования материала при одноосном сжатии и растяжении одинаковы (рис.17.3, б). При принятых предположениях следует полагать, что нейтральная линия совпадает с осью симметрии x (рис.17.3, а)

Как и при упругом изгибе в данном случае будет исходить, что и при упруго-пластическом изгибе справедлива гипотеза плоских сечений, т.е.:

где  - кривизна нейтральной оси изогнутого бруса, а y - расстояние точек от нейтральной оси.

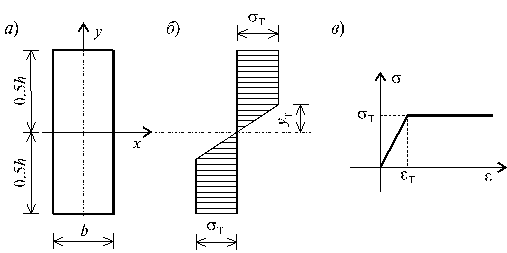
Рис.17.3

Упруго-пластическая стадия деформирования поперечного сечения бруса делится на две зона: упругую и пластическую. Величина , определяющая расстояние границы этих зон от нейтральной линии определяется по (17.26):

По мере увеличения изгибающего момента и соответственно кривизны, величина уменьшается за счет сокращения высоты упругой зоны.

Выражение изгибающего момента в данном случае можно преобразовать в следующем виде:

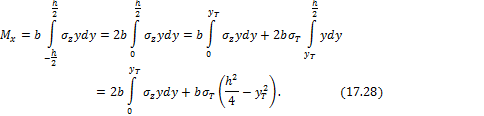
Так как из теории изгиба, для упругого участка, выполняется соотношение:

Подставляя последнее в (17.28) и после интегрирования получим:

Учитывая, что , получим:

откуда

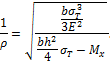
Из последнего выражения следует, что кривизна бруса с увеличением момента М_x возрастает и обращается в бесконечность, при

В этом случае , следовательно, и как это следует из (17.27) . Следовательно, все сечение охватывается пластической деформацией. Несущая способность сечения в данном случае исчерпана. Из (17.29) можно определить:

Здесь носит название пластического момента сопротивления сечения.

Обобщая выражения (17.29) с известным аналогичным соотношением теории изгиба , можно установить, что при значениях момента в поперечном сечении балки возникает пластическая деформация, а значение следует рассматривать как предельное значение момента, при котором несущая способность конструкций в данном сечении исчерпана.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00