Главная
17.4.
Основы теории ползучести
В физических уравнениях теории упругости и теории пластичности введено допущение, что при действии внешних сил тело деформируется мгновенно. Однако, в действительности полная деформация любой точки заданного тела при действии внешних сил, формируется в течении определенного промежутка времени. Далее известно, что все материалы обладают свойством старения, т.е. физико-механические характеристики во времени меняются, поэтому учет временных процессов, протекающих в элементах конструкций в период действия внешних сил имеет важное значение в плане совершенствования методов их расчета.
Свойства материалов связанные с деформацией во времени при действии внешних постоянных нагрузок называются ползучестью.
Явление ползучести в принципе присуще всем материалам. Учет фактора ползучести имеет существенное значение для правильного работы конструкций при действии внешних сил.
Предположим, что в начальный момент времени деформации имеют значения e(0), равное упругой деформации или суммарной упругой и пластической деформацией (рис.17.4).
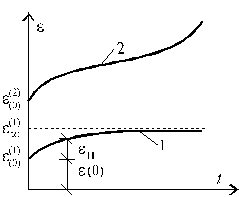
Рис.17.4
С увеличением времени t наблюдается возрастание деформаций.
Если процесс сопровождается уменьшением скорости деформирования ![]() и при t®¥,
и при t®¥,
![]() ®0, то
ползучесть называется установившейся
(1) (рис.17.4) Если деформация ползучести имеет тенденцию к беспредельному
увеличению и в итоге сопровождается разрушением материалов конструкции, то
данный вид ползучести называется неустановившейся
(2) (рис.17.4).
®0, то
ползучесть называется установившейся
(1) (рис.17.4) Если деформация ползучести имеет тенденцию к беспредельному
увеличению и в итоге сопровождается разрушением материалов конструкции, то
данный вид ползучести называется неустановившейся
(2) (рис.17.4).
Полная деформация в произвольный момент
времени определяется как сумма начальной деформации e(0)
и деформации ползучести ![]() , т.е.
, т.е.
![]() .
(17.29)
.
(17.29)
Заметим, что характер протекания ползучести во времени очень чувствителен в зависимости об интенсивности напряжений и температуры. Увеличение интенсивности напряжений или градиента температуры, как правило, приводит к возрастанию деформаций ползучести.
Если увеличение деформаций ползучести пропорционально увеличению напряжений, то имеем дело с линейной ползучестью, в противном случае - с нелинейной ползучестью.
Если в некоторый момент времени ![]() > 0 производить разгрузку, то накопленная деформация
ползучести начинает уменьшаться, асимптотически стремясь к некоторому пределу
> 0 производить разгрузку, то накопленная деформация
ползучести начинает уменьшаться, асимптотически стремясь к некоторому пределу ![]() рис.17.5. Такое
явление носит название обратной ползучести. В частном случае, при линейной
ползучести деформация e¥ при полной
разгрузке может стремиться к нулю, т.е. образец во времени полностью восстанавливает
свои первоначальные размеры. Это свойство материала называется последействием.
рис.17.5. Такое
явление носит название обратной ползучести. В частном случае, при линейной
ползучести деформация e¥ при полной
разгрузке может стремиться к нулю, т.е. образец во времени полностью восстанавливает
свои первоначальные размеры. Это свойство материала называется последействием.
При ползучести предполагается неизменность величин напряжений и рассматриваются изменения деформаций во времени.
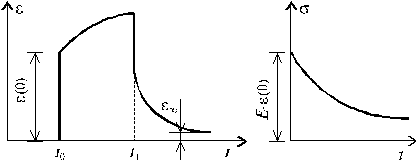
Рис.17.5
Рис.17.6
Обратимся к другому случаю, характеризующему
свойства материалов и тесно связанному с ползучестью. Если имеется образец и
обеспечить постоянство деформаций во времени в образце, как показывают
эксперименты, то во времени происходит снижение напряжений (рис.17.6). Явления
медленного уменьшения напряжений в образце при постоянной деформации называется
релаксацией.
При линейной ползучести, если материал конструкции не обладает свойством старения, зависимость между напряжениями и деформацией можно представить в следующем виде:
![]() ,
(17.30)
,
(17.30)
где
![]() ;
; ![]() - определяет
деформацию ползучести при единичном напряжении s = 1;
- определяет
деформацию ползучести при единичном напряжении s = 1;
![]() .
.
Для функции ![]() справедливо равенство с(0) = 0.
справедливо равенство с(0) = 0.
Теория ползучести,
учитывающая предысторию нагружения называется
наследственной теорией ползучести.
Связь между напряжением и деформациями по наследственной теорией ползучести записывается в виде:
![]() .
(17.31)
.
(17.31)
Функция
![]() может иметь различные
представления, в частности:
может иметь различные
представления, в частности:
![]() ,
(17.32)
,
(17.32)
где g, k - постоянные коэффициенты, характеризующие свойства материалов.
Если учесть свойства старения материалов, т.е. свойства материалов изменяющиеся во времени, но величина и упругие деформации и деформации ползучести конструкций зависят от возраста материала. В этом случае физические уравнения можно представить в следующем виде:
![]() ;
; ![]() ,
(17.33)
,
(17.33)
где ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Здесь a, b, n, A, B, g - постоянные характеристики материалов конструкций.
В общем случае, когда переменными являются как напряжение так и деформация соотношения между ними с учетом свойства наследственности и строения в рамках линейной теории записывается в виде:
![]() .
(17.34)
.
(17.34)
Здесь вводим обозначения:
![]() . (17.35)
. (17.35)
Линейное соотношение между напряжениями и деформациями (17.34) отличается от закона Гука для упругого материала только тем, что вместо величины 1/E здесь имеется интегральный оператор. Отсюда следует следующее простое правило построения решения задачи теории линейной ползучести, которое носит название принцип Вольтерра.
Решение задачи по теории линейной ползучести может быть получено из решения аналогичной задачи в упругой постановке, далее следует заменить упругие постоянные интегральные операторы и произвести необходимые операции над ними.
В частности, если в известных упругих решениях предполагать, что они записаны в изображениях Лапласа, т.е. заменить упругие постоянные изображениями соответствующих операторов теории ползучести и применить операции переходов от изображений к оригиналам искомых функций, получим решение соответствующее задаче с учетом ползучести материалов конструкции.
Отметим, что в настоящее время при решении многих инженерных задач, как в области механики твердого деформируемого тела, так и других отраслях, широко применяется метод интегрального преобразования Лапласа. Этот метод особенно эффективен при решении линейных дифференциальных, интегро-дифференциальных и интегральных уравнений, а также систем, состоящих из вышеуказанных типов уравнений. Суть его является следующей.
Если имеется некая искомая функция y(t) от действительной переменной t, обозначая через y(s) образ искомой функции комплексной переменной s, т.е. изображение заданной функции по Лапласу, тогда формулы по определению оригинала и его изображения имеют следующие представления:
![]()
![]() .
.
где i - мнимая единица, а c - некоторая постоянная, на действительной оси.
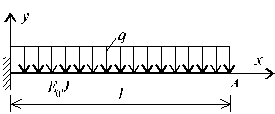
Рис.17.7
В качестве примера реализации изложенного подхода при решении инженерных задач рассмотрим расчет прогиба свободного конца консольной балки (рис.17.7), в момент времени t = 0 загруженной равномерно распределенной нагрузкой, постоянной во времени. Материал балки характеризуется линейной ползучестью, для которого
![]() .
.
По методу начальных параметров в упругой постановке задачи решение записывается в виде:
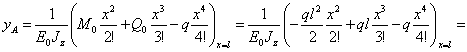
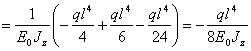 . (17.36)
. (17.36)
Заменим
![]() на
на ![]() .
.
Тогда выражения перемещения (17.36) в изображениях Лапласа принимает вид:
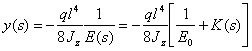 .
(17.37)
.
(17.37)
Здесь К(s) определяется из (17.32):
![]() .
(17.38)
.
(17.38)
С учетом (17.38), (17.37) принимает вид:
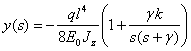 .
.
Выполняя операции обратного преобразования Лапласа, получим:
![]() . (17.39)
. (17.39)
Отсюда следует, что при действии постоянной нагрузки прогиб балки с течением времени возрастает по экспоненциальному закону и при t®¥ принимает следующее предельное значение:
![]() ,
,
где
![]() - упругое
перемещение, т.е. перемещение балки в точке А при t = 0.
- упругое
перемещение, т.е. перемещение балки в точке А при t = 0.
17.5. Расчет
перемещения балки с учетом ползучести
Для металлической двухпролетной
балки (рис.17.8, а), при следующих
исходных данных: q = 2 кН/м;
Р = 10 кН; J = 20×10-4
м4; Е0 = 2×108 кН/м2; а = 3 м; g = 2×10-2
1/cут; k = 1.3; ![]()
![]() требуется определить перемещение
за счет изгиба конструкции в сечениях А и С, предполагая
материал конструкции упругим, далее - линейно
ползучим.
требуется определить перемещение
за счет изгиба конструкции в сечениях А и С, предполагая
материал конструкции упругим, далее - линейно
ползучим.
Решение:
1. Определить перемещение в точках А и С за счет изгибаемых упругих деформаций конструкции

Рис.17.8
Учитывая, что заданная система один раз статически неопределима, решение задачи рассмотрим по методу сил.
Основная система изображена на рис.17.8, б. Эпюра моментов в основной системе от заданной системы внешних сил и единичной вертикальной силы X = 1, приложенной в месте и по направлению, отображенной связи показана на рис.17.8, в, г.
Перемножая эпюры моментов изображенных на рис.17.8, в, г по формуле Мора, последовательно определим вертикальное перемещение т.В от действия силы X = 1 и от действия системы внешних сил:
![]() ;
;
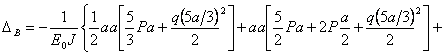
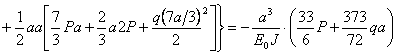 .
.
Опорная реакция в точке В принимает значение:
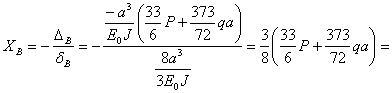
![]() кН.
кН.
Далее вычисляются опорные реакции в заделке:
![]()
![]()
![]() кНм;
кНм;
![]()
![]() , откуда
, откуда
![]() кН.
кН.
Проверяем правильность вычисления величины опорных реакций:
![]()
По методу начальных параметров последовательно определим величины упругих перемещений в точке А и С:
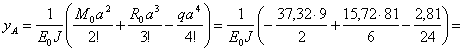
![]() м;
м;
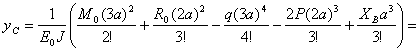
![]()
![]() м.
м.
2. Определить
перемещение в точках А и С с
учетом ползучести материала конструкции
Запишем выражения упругого перемещения:
![]() ;
; ![]() .
.
По аналогу этих формул, запишем выражения перемещений с учетом ползучести материала балки в изображениях Лапласа:
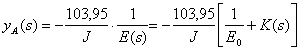 ;
;
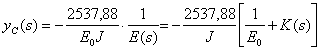 . (17.40)
. (17.40)
Применяя изображения Лапласа
запишем выражение функции ![]() в изображениях в виде
(17.38):
в изображениях в виде
(17.38):
Подставляя (17.38) в (17.40) получим:
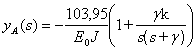 ;
; 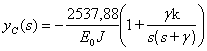 .
.
Переходя к оригиналам окончательно получим:

В условиях установившейся ползучести, при ![]() из последних выражений
вычисляются результирующие перемещения:
из последних выражений
вычисляются результирующие перемещения:
![]() м;
м;
![]() м.
м.
Как показывают численные расчеты за счет неограниченной ползучести перемещение заданной системы возросло в 2,3 раза:
![]() ;
; ![]() .
.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Теория машин и механизмов