Главная

83. Расчет конструкций по методу предельного равновесия

Содержание

Основные положения метода предельного равновесия

Основы теории пластичности

Определение предельного состояния системы при растяжении-сжатии

Предельное состояние статически определимых систем при кручении

Предельное состояние статически определимых систем при изгибе

Расчет статически неопределимых балок по предельному состоянию.

Кинематический и статический способ

Вопросы для самопроверки

Основным методом расчета конструкций промышленных и гражданских зданий и сооружений, мостов и др. в настоящее время является метод предельных состояний. Этот метод был разработан учеными под руководством проф. Н.С. Стрелецкого и начал применяться с 1955 г.

Предельным считается состояние, при котором конструкция перестает удовлетворять эксплуатационным требованиям или требованиям, предъявляемым в процессе возведения здания и сооружения.

Различают две группы предельных состояний: первая – непригодность к эксплуатации по причинам потери несущей способности; вторая – непригодность к нормальной эксплуатации в соответствии с предусмотренными технологическими или бытовыми условиями. В правильно запроектированном сооружении не должно возникнуть ни одно из указанных предельных состояний, т.е. должна быть обеспечена его надежность. Надежностью называется способность объекта сохранять в процессе эксплуатации качество, заложенное при проектировании.

Факторы, от точного учета которых зависит уровень надежности сооружения или отдельного его элемента, следующие: нагрузки и другие воздействия, механические свойства материала, геометрические параметры конструктивных элементов, условия работы, степень ответственности сооружения и др.

Нормативное значение нагрузки и воздействий соответствует их значению при нормальной эксплуатации. Они устанавливаются Строительными нормами и правилами (СНиП). Возможное отклонение значений нагрузок от их нормативных значений учитывается коэффициентом надежности по нагрузке n≥1, принимаемым по СНиПу.

Нагрузки и воздействия, полученные путем умножения их нормативных значений на коэффициент надежности по нагрузке, называются расчетными. Например, расчетная сила P=nP_н.

При расчете по первой группе предельных состояний обычно n>1, и тогда расчетные нагрузки являются наибольшими нагрузками, которые могут возникнуть за время эксплуатации сооружения.

Но коэффициент надежности по нагрузке может быть меньше единицы, т.е. n<1, если это приводит к ухудшению условий работы сооружения. Например, кратковременные нагрузки в стадии возведения принимаются с коэффициентом n=0,8.

Коэффициент надежности по нагрузке при расчете по второй группе предельных состояний принимается, как правило, равным единице.

Основной характеристикой сопротивления материалов силовым воздействиям является нормативное сопротивление R_н, которое устанавливается СНиПом с учетом условий контроля и статистической изменчивости механических свойств материала. В качестве нормативного сопротивления строительных сталей принимают наименьшее контролируемое (браковочное) значение предела текучести σ_T или временного сопротивления σ_в. Эти значения устанавливаются ГОСТами или техническими условиями на металл.

Возможное отклонение в неблагоприятную сторону от значений нормативного сопротивления учитывается коэффициентом надежности по материалу γ_м>1. Этот коэффициент отражает статистическую изменчивость свойств материала и их отличие от свойств отдельно испытанных образцов. Например, для металла γ_м =1,025…1,15; для бетона γ_м =1,3…1,5.

Величина, полученная в результате деления нормативного сопротивления на коэффициент надежности по материалу, называется расчетным сопротивлением:

Она представляет собой наименьшую возможную величину нормативного сопротивления; значения для R устанавливаются СНиПом.

Особенности действительной работы материалов, элементов конструкций, их соединений учитываются коэффициентом условий работы γ. Он отражает влияние температуры, агрессивности среды, длительности и многократной повторяемости воздействия, приближенности расчетных схем и условность расчетных предпосылок (γ<1), а также перераспределение усилий при развитии пластических деформаций и другие благоприятные факторы (γ>1). Числовые значения для устанавливаются СНиПом на основании экспериментальных и теоретических исследований и вводятся в качестве множителя к значению расчетного сопротивления R. В большинстве случаев при нормальных условиях работы коэффициент γ=1 и может быть опущен.

Степень ответственности и капитальности сооружений, а также значимость последствий тех или иных предельных состояний учитывается коэффициентом надежности по назначению γ_н≤1. Его вводят в качестве делителя к значению расчетного сопротивления или в качестве множителя к значению расчетных нагрузок, воздействий и усилий.

Существуют и другие коэффициенты, которые учитывают особенности расчета и работы сооружения, например коэффициент n_c, учитывающий одновременное действие всех расчетных нагрузок. Здесь же приведены коэффициенты, учитывающие основные факторы, которые влияют на надежность сооружения.

Надежность и гарантия от возникновения предельных состояний первой группы (по несущей способности) обеспечиваются выполнением следующего условия:

где N - усилие, действующее в рассчитываемом элементе конструкции (функция нагрузок и других воздействий); S - предельное усилие, которое может воспринять рассчитываемый элемент (функция физико-механических свойств материала, размеров элемента и условий работы).

Усилие N, являющееся наибольшим возможным усилием (воздействием) за время нормальной эксплуатации конструкции, определяется так:

а предельное усилие

где - геометрическая характеристика сечения.

Таким образом, условие прочности (надежности) для центрально растянутого (сжатого) элемента () будет иметь вид

83.1. Основные положения метода предельного равновесия

Расчет конструкций в упругой постановке задачи, как известно, проводится по методу допускаемых напряжений. Данный подход при расчете статически определимых и статически неопределимых систем не позволяет найти их истинный запас прочности, так как исчерпание несущей способности конструкции сопровождается появлением в ней пластических деформаций. Для выявления истинного запаса несущей способности конструкции необходимо проводить расчет с учетом упруго-пластических деформаций. Однако сложность аппарата теории пластичности не позволяет решать широкий круг очень важных инженерных задач. В этом отношении расчет конструкций по методу предельного равновесия, позволяет дополнить существующий пробел по данному вопросу. Поэтому, метод расчета конструкций по предельным состояниям, по сравнению с упругим расчетом, является важным этапом для оценки истинных запасов прочности конструкции. При этом следует отметить, что расчет конструкций по методу предельных состояний является приближенным в том контексте, что, в отличии от упруго-пластического расчета, не позволяет описать процесс перехода от упругого к предельному состоянию.

Если при проектировании инженерных сооружений необходимо знать процесс формирования напряженно-деформированного состояния вплоть до исчерпания несущей способности конструкций, метод предельного равновесия неприменим. Однако, в тех случаях, когда необходимо определить только несущую способность конструкции этот метод является очень эффективным и имеет важное практическое значение.

При расчете конструкций по допускаемым напряжениям в упругой постановке задачи, как известно, предельной нагрузкой считается та, при которой наибольшее напряжение , хотя бы в одной точке опасного сечения достигает величины . При этом вводится понятие о допускаемом напряжении, определяемом по формуле , где n - коэффициент запаса.

При расчете конструкций по методу предельного равновесия предполагается двухстадийный характер деформирования материала: в первой стадии материал подчиняется закону Гука, пока напряжения не достигнут предела текучести; а затем во второй стадии, предполагая, что в нем в определенной стадии нагружения в опасных сечениях беспредельно развиваются пластические деформации при постоянном напряжении. С появлением пластических деформаций нарушается линейная зависимость между напряжениями и деформациями по закону Гука, и все расчетные формулы, вывод которых основан на этой зависимости, становятся неприменимыми. Нарушается прямая пропорциональность между действующими на элемент конструкции нагрузками и возникающими в нем напряжениями и деформациями. Становится неприменимым один из основных принципов сопротивления материалов – принцип независимости действия сил.

Так как зависимость между напряжениями и деформациями становится нелинейной и для каждого материала определяется видом диаграммы растяжения, единых для различных материалов расчетных формул, учитывающих пластические деформации, получить невозможно. При выводе расчетных формул диаграммы растяжения упрощают (схематизируют). Для материалов, имеющих площадку текучести, например для низкоуглеродистых сталей условная диаграмма зависимости напряжения от деформации состоит из наклонного и горизонтального участков и носит название диагpаммы идеально yпpyго-плаcтичеcкого тела, или диагpаммы Пpандтля.

Суть метода состоит в том, что конструкция рассматривается в момент, непосредственно предшествующий ее разрушению, когда еще выполняются условия равновесия для внутренних и внешних сил, достигающих предельных значений. Отсюда и произошло название метода предельного равновесия.

Реальные конструкции представляют собой в большинстве случаев многократно статически неопределимые системы, материал которых обладает свойством пластичности. Благодаря этому конструкции обладают дополнительными резервами несущей способности. После того, как в наиболее опасных сечениях напряжения достигают предела текучести, в отличие от статически определимых систем, статически неопределимые системы могут нести дополнительные нагрузки за счет перераспределения внутренних сил.

Для пластичного материала предельным обычно считается, напряженное состояние, которое соответствует возникновению заметных остаточных деформаций, а для хрупкого - такое, при котором начинается разрушение материала.

Для выполнения расчетов на прочность по методу предельного равновесия вводятся понятия коэффициента запаса прочности и эффективное напряжение.

Коэффициент запаса при данном напряженном состоянии это число, показывающее во сколько раз следует одновременно увеличить все компоненты тензора напряжений, чтобы оно стало предельным.

Эквивалентное напряжение - это такое напряжение, которое следует создать в растянутом образце, чтобы его напряженное состояние было равноопасно с заданным.

Для пластичных материалов критерием наступления предельного состояния принимается состояние, при котором максимальные касательные напряжения достигают некоторого предельного значения:

Гипотеза максимальных касательных напряжений, приемлемая для пластичных материалов, обнаруживает заметные погрешности для материалов, имеющих различные механические характеристики при сжатии и растяжении.

В таких случаях применяется энергетическая гипотеза, согласно которой предельное состояние в точке наступает тогда, когда энергия формоизменения

принимает некоторое заранее заданное значение. Это предельное значение для определяется следующим образом. Для простого растяжения выражение (83.2) принимает вид:

В сложном напряженном состоянии принимает значение

При совместном рассмотрении (83.2) и (83.3) получим:

Следует помнить, что расчет по методу предельного равновесия можно выполнять только для элементов конструкций, изготовленных из пластичных материалов, допускающих пластические деформации в наиболее напряженных точках без появления в них трещин. Недопустимо появление пластических деформаций в деталях машин, длительно работающих при переменных, циклических напряжениях, так как при этом резко снижается число циклов до разрушения, т.е. долговечность детали.

83.2. Основы теории пластичности

Рассмотрим основные особенности характера деформирования материалов при их нагружении в упруго-пластической стадии. При напряжениях, превышающих предел упругости, после разрузки наблюдаются заметные остаточные деформации. Свойство материалов относительно неспособности восстанавливать первоначальные размеры образцов после их разгрузки за счет возникновения остаточных деформаций, называется пластичностью.

Физические соотношения, взятые в основу теории, позволяющие определить переход напряженно-деформированного состояния от упругой стадии к упруго-пластической и описать процесс деформирования тела с учетом пластических свойств материалов, называются теорией пластичности.

Учет пластических свойств материалов является чрезвычайно важным этапом в плане совершенствования методов расчета конструкций. Если конструкции из хрупких материалов вплоть до стадии разрушения при действии внешних сил не развивают заметных пластических деформаций, то для конструкций из пластических материалов основные деформации формируются именно за счет возникновения пластических деформаций. Так например, полные деформации, соответствующие концу площадки текучести на реальной диаграмме, для многих материалов в 30 - 40 раз превышают деформации, соответствующие концу линейного участка.

В настоящее время существуют две теории пластичности. Их различие заключается в конкретной записи физических соотношений.

В деформационной теории пластичности, разработанной А.А.Ильюшиным, взамен закона Гука устанавливаются новые соотношения между напряжениями и деформациями.

Во второй теории - теории течения, физические соотношения связывают напряжения с приращениями деформаций или скоростями деформаций.

Как показывают экспериментальные исследования, деформационная теория пластичности справедлива при относительно небольших пластических деформациях для простого нагружения, т.е. когда все внешние нагрузки изменяются пропорционально во времени.

Теория течения является эффективным при изучении процессов, связанных с возникновением больших деформаций и при сложном нагружении, т.е. когда нагрузки, прикладываемые к телу, изменяются во времени независимо друг от друга.

Здесь ограничимся рассмотрением только деформационной теории пластичности.

Процесс деформирования материалов можно условно разделить на две стадии. Начальная стадия - упругое деформирование. Компоненты тензоров напряжений и деформаций при этом связаны законом Гука. Для реальных инженерных задач, связанных с определением напряженно-деформированного состояния тела, как в упругой, так и в упруго-пластической стадии деформирования, предварительно необходимо установить: во-первых, условие перехода от упругой стадии деформирования к пластической стадии и, во-вторых, установить физические зависимости во второй стадии деформирования.

Условия перехода от упругого состояния к пластическому могут быть определены по формулам одной из гипотез метода предельного равновесия.

Как это было изложено в пункте «Основные положения метода предельного равновесия», наиболее приемлемыми являются гипотезы максимальных касательных напряжений и энергии формоизменения. При этом, для построения соотношений пластичности гипотеза энергии формоизменения является наиболее приемлемой, согласно которой переход из упругого состояния в пластическое происходит тогда, когда величина

называемая интенсивностью напряжений, достигает определенной величины, равной пределу текучести материала при одноосном напряженном состоянии, т.е.

С учетом физических соотношений закона Гука выражение (83.4) принимает вид:

где принято обозначение:

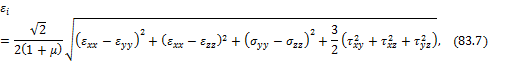
называемое интенсивностью деформаций.

Следовательно, соотношение (83.6), следует рассматривать как одну из форм выражения обобщенного закона Гука.

Выражения интенсивности напряжений и интенсивности деформаций, записанные через главные напряжения и деформации можно представить в виде:

В основу деформационной теории пластичности заложены следующие гипотезы.

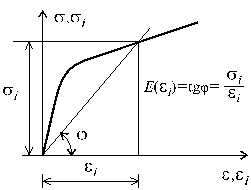
Рис. 83.1

Первая гипотеза устанавливает связь между интенсивностью напряжений и интенсивностью деформаций (рис. 20.1), и гласит, что она не зависит от вида напряженного состояния, т.е.

где - является переменной величиной и зависит от значения . Соотношение (83.9) является единым для всех видов напряженного состояния.

Согласно второй гипотезе - изменение объема является чисто упругой. Это положение хорошо согласуется с экспериментальными данными, так как при всестороннем сжатии в материалах заметных пластических деформаций не обнаруживается.

При деформировании материалов пластические деформации, как правило, существенно больше упругих и, учитывая, что объемная деформация e является величиной порядка упругих удлинений, поэтому принимается, что при пластическом деформировании изменение объема пренебрежительно мало. На основании этого положения вводится гипотеза, что в пластической стадии деформирования материал считается несжимаемым.

Откуда следует, что в пластической стадии деформирования можно коэффициент Пуассона принимать равным μ = 0,5.

Сначала определим физические соотношения при одноосном растяжении, когда

Из (83.4) и (83.7), соответственно получим и , что подтверждает первое положение теории, что аналитическое выражение (83.9) едино для всех видов напряженного состояния. Данное обстоятельство позволяет определить переменный модуль деформирования по диаграмме , т.е. .

В заключение, запишем физические соотношения между напряжениями и деформациями при пластической стадии деформирования тела:

где является модулем деформации при сдвиге, который определяется следующим образом:

Приведенные физические соотношения деформационной теории пластичности являются справедливыми при простых нагружениях, т.е. только в тех случаях, когда все внешние силы на всех этапах нагружения во времени изменяются пропорционально. В данном случае заметим, что главные оси напряженного состояния при изменении внешних сил сохраняют свое направление независимо от стадии деформирования.

Для наглядности ниже рассмотрим наиболее представительные примеры расчета конструкций по методу предельного равновесия.

83.3. Определение предельного состояния системы при растяжении-сжатии

Для статически определимой системы, в элементах которой возникают лишь продольные усилия, расчеты на прочность по допускаемым напряжениям и по предельным нагрузкам дают один и тот же результат. Результаты аналогичных расчетов статически неопределимой системы различны.

Пример 1.

Рассмотрим систему, представляющую собой абсолютно жесткую балку, с одним концом шарнирно опертую, и подвешенную на трех одинаковых идеально упруго-пластических подвесках, длиной l, площадью поперечного сечения А, модулем упругости материала Е, при заданной схеме нагружения силой Р (рис.83.2, а). Заданная система дважды статически неопределима.

Решение.

По мере роста силы P, подвески 1, 2, 3 поэтапно будут переходить в пластическое состояние, причем напряжения в каждой подвеске не могут превышать .

Выделим следующие стадии деформирования заданной системы.

Первая стадия: все подвески работают упруго. Для определения реакций в подвесках составляем уравнение равновесия:

Рис. 83.2

Для определения величин усилий в подвесках N₁, N₂ и N₃ необходимо составить еще два уравнения совместности. Учитывая, что балка абсолютно жесткая и деформации в подвесках пропорциональны возникающим в них усилиям, то из условия подобия треугольников (рис.83.2, б), имеем:

откуда

Тогда из (83.12) с учетом (83.13) определяются реакции во всех подвесках:

Вторая стадия: при некотором значении P, сначала наиболее нагруженная первая подвеска, переходит в пластическое состояние, то есть (рис.83.2, в). При этом из (83.13) можно установить, что в остальных подвесках усилия будут равны:

Подставляя значения усилий в уравнение равновесия (83.12), получим:

откуда и определим величину внешней силы Р, при котором система переходит во второе состояние:

Третья стадия: при дальнейшем росте значения силы P, и вторая подвеска переходит в пластическое состояние, то есть (рис.83.2, г). При этом, из второго и третьего соотношения (83.14), значение усилия в третьей подвеске будет равно:

Из уравнения равновесия (83.12), с учетом значения усилий в подвесках в третьем состоянии, получим:

Четвертая стадия - предельное состояние: в этом состоянии усилия во всех трех подвесках равны своему предельному значению, т.е. (рис.83.2, д). Уравнение равновесия (83.12), при этом принимает вид:

откуда и определяется предельная величина внешней силы:

Далее определим перемещение f_i балки в точке приложения внешней силы P в различных стадиях работы заданной системы.

При переходе заданной системы от первого стадии деформирования ко второму, имеем:

При переходе заданной системы от второй стадии к третьей, имеем:

И наконец, при переходе системы от третьей стадии к предельному состоянию, получим:

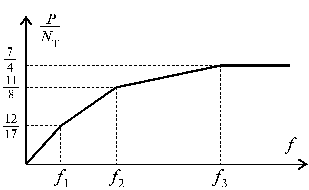
Рис. 83.3

Зависимость f от P показана на рис. 83.3. Она изображается ломаной линией, которая после предельного равновесного состояния становится горизонтальной, то есть после того, как напряжения достигнут предела текучести во всех трех подвесках. Откуда следует, что при постоянной , перемещение f беспредельно возрастает, т.е. происходит разрушение системы.

Как видно из приведенного примера, расчет даже для такой простой системы оказывается довольно громоздким, хотя он дает возможность находить не только предельную силу, но и описать поведение конструкции в процессе ее нагружения. На практике, при расчете систем с учетом пластических деформаций рассматривают только предельное состояние.

Пример 2.

Для трехстержневой системы (рис. 83.4, а) при условии, что диаграмма растяжения для стержней имеет участок упрочнения (рис. 83.4, б), при следующих исходных данных: α = 30°; l = 1,0 м; А = 2∙10^-4 м² - площади поперечных сечений стержней; E = 2∙10⁸ кН/м² - модуль упругости материалов стержней; = 2,5∙10⁵кН/м² - предел упругости материала; = 3,9∙10⁵ кН/м² - временное сопротивление; = 0,02 - значение деформации, соответствующее напряжению требуется:

1. Определить абсолютные и относительные удлинения стержней и значение силы P = P₁, при котором в наиболее напряженном стержне напряжения достигают предела упругости.

2. Определить абсолютные и относительные удлинения стержней и значение силы P = P₂, при котором все элементы заданной системы переходят в пластическую стадию деформирования.

3. Определить абсолютные и относительные удлинения стержней и значение силы P = P₃, при котором в наиболее напряженном стержне напряжения достигают значения, равного временному сопротивлению , т.е. при дальнейшем увеличении силы P происходит разрушение заданной системы.

Решение.

1. Определить абсолютные и относительные удлинения стержней и значение силы P = P₁, при котором в наиболее напряженном стержне напряжения достигают предела упругости. Заданная система (рис.83.4, а) один раз статически неопределима. Применяя метод сечений (рис.83.4, б) и составляя уравнения равновесия статики, последовательно можем определить:

или

Рис. 83.4

Согласно деформированной схеме, изображенной на рис.83.4, а, из геометрических соображений, уравнения для определения относительных деформаций записываются в виде:

С учетом , и принимая во внимание, что на первом этапе нагружения все элементы заданной системы деформируются согласно закону Гука, т.е. , получим:

С учетом (83.23) из (83.21) и (83.22) можно получить следующую замкнутую систему уравнений относительно усилий N₁ и N₂:

Откуда определяются:

Для выражения напряжения в среднем в элементах заданной системы имеем:

Откуда следует, что . Следовательно, в процессе нагружения сначала средний стержень переходит в пластическую стадию деформирования, а затем боковые стержни, т.е. при всех нагружения средний стержень, вплоть до стадии разрушения заданной системы, будет наиболее напряженным.

Принимая в (83.25), что и P = P₁, окончательно получим:

Абсолютные удлинения стержней принимают значения:

Относительные удлинения стержней принимают значения:

2. Определить абсолютные и относительные удлинения стержней и значение силы P = P₂, при котором все элементы заданной системы переходят в пластическую стадию деформирования. Физические уравнения взамен закона Гука в случае, когда стержни переходят в пластическую стадию деформирования, т.е. при , , в данном случае записываются в виде:

которое представляет собой уравнение прямой линии, описывающей диаграмму деформирования в области пластических деформаций (рис.83.4, в).

В начале по очевидным соотношениям определяется значение деформаций , соответствующее началу пластической стадии деформирования стержней и модуля деформаций в пластической стадии их деформирования:

Заметим, что на данном этапе нагружения, т.е. когда , боковые элементы заданной системы деформируются упруго, а средний элемент - будет находиться в пластическом состоянии.

Учитывая, что при P = P₂ будем иметь , , последовательно определим значения усилий и абсолютное удлинение в боковых стержнях при их переходе в пластическую стадию деформирования:

Учитывая выражения (83.22) и (83.26) определяется значение абсолютного и относительного удлинения, а также усилия в среднем стержне, в момент перехода боковых стержней в пластическую стадию их деформирования:

Далее из уравнения равновесия (83.21) вычисляется величина внешней силы P = P₂:

3. Определить абсолютные и относительные удлинения стержней и значение силы P = P₃, при котором в наиболее напряженном стержне напряжения достигают значения, равного временному сопротивлению , т.е. при дальнейшем увеличении силы P происходит разрушение заданной системы. Сначала вычисляем значения удлинений в боковых стержнях, при достижении в среднем стержне предельных напряжений и деформаций , .

Учитывая, что получим:

Таким образом, к моменту разрушения среднего стержня (, ) боковые стержни также находятся в пластической стадии деформирования. Напряжения в боковых стержнях, в момент разрушения среднего стержня, принимают значения:

Для определения величины внешней силы P = P₃, т.е. значения силы в момент разрушения среднего стержня из уравнения равновесия (83.21) имеем:

Как показывают результаты расчетов, для перехода среднего стержня в пластическую стадию деформирования необходима была внешняя сила P = P₁= 119,5 кН, а для его разрушения - P = P₃= 200,97 кН.

На основании полученных результатов можно заметить, что если бы мы ограничивались только учетом упругой стадии работы конструкции, т.е. P £ P₁, то несущая способность заданной системы оценивалась бы как P = P₁= 119,5 кН.

Как показали расчеты, учет пластической стадии работы позволил выявить дополнительные резервы несущей способности заданной системы, т.к. величина разрушающей силы заданной системы в действительности равна P = P₃= 200,97 кН.

В заключении определим величины абсолютных удлинений стержней в момент разрушения среднего стержня:

Легко определить во сколько раз абсолютные удлинения стержней возросли за счет возникновения пластических деформаций по отношению к их абсолютным удлинениям в момент перехода среднего стержня от упругой к пластической стадии деформирования:

4. Рассматривая систему (рис.83.4, а) при отсутствии среднего стержня в процессе ее нагружения, определить абсолютные и относительные удлинения элементов системы, и внешней силы P = P₄, при котором в ее элементах напряжения достигают значения, равного временному сопротивлению . Исключая средний стержень, система превращается из статически неопределимой в статически определимую. Применяя метод сечений, легко установить, что уравнения равновесия в данном случае принимают следующий вид:

В конце упругой стадии работы элементов заданной системы имеем, что , . С учетом данного обстоятельства последовательно определим значение усилия N₁, абсолютное удлинение стержней и величину силы P = P₁, соответствующих концу упругой стадии работы данной системы:

При дальнейшем нагружении системы, то есть при P > P₁= 86,6 кН, элементы данной системы переходят в пластическую стадию деформирования. Последовательно определим значение внутренних усилий, абсолютных удлинений и величину разрушающей силы P = P₂, при достижении напряжений и деформаций предельных значений. Т.е. при , :

Анализируя полученные результаты, можно сделать следующие выводы.

Как и для трехстержневой статически неопределимой системы, так и для двухстержневой статически определимой системы, учет пластических деформаций позволил выявить дополнительные резервы систем по несущей способности. Если бы мы ограничились только упругим расчетом, расчетная несущая способность двухстержневой системы была бы равна P = P₁= 86,6 кН. А за счет учета упруго-пластической работы элементов системы, как было показано, несущая способность будет исчерпана при P = P₂= = 135,1 кН, т.е. при нагрузке в 1,56 раза больше, чем при упругом расчете.

Далее заметим, что за счет удаления одного среднего элемента из исходной системы, несущая способность и жесткость системы, соответственно, уменьшилась в 200,96/135=1,49 и в

Пример 3.

Определить предельную нагрузку F_u для стержневой системы, показанной на рис.83.5. Предел текучести материала стержней принять = 2900 кг/см².

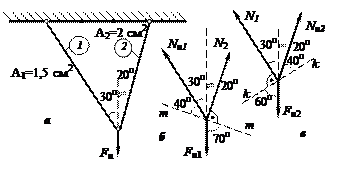
Рис.83.5

Решение.

Пусть течет стержень 1 (рис. 83.5, а), тогда

Спроектируем все силы на ось m–m (рис. 83.5, б):

откуда находим

Если же предположить, что течет стержень 2, то будем иметь

Спроектируем все силы на ось k–k (рис.83.5, в):

откуда определяем

Таким образом, получили два значения предельной нагрузки

F_u₁ = 9743 кг и F_u₂ = 8886 кг,

из которых истинное значение предельной нагрузки будет наименьшим:

Пример 4.

Дано А₁ = 4 см², А₂ = 3 см², А₃ = 2 см², = 285 МПа.

Определить предельную нагрузку F_u для системы стержней (рис. 83.6, а).

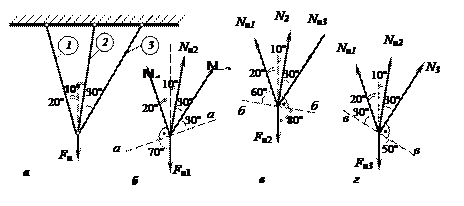
Рис.83.6

Решение.

Определим предельные нормальные усилия, которые могут возникнуть в стержнях системы:

Для образования механизма рассматриваемой системы достаточно течения каких-либо двух стержней. Возможны три механизма разрушения.

Первый механизм разрушения. Пусть текут стержни 2 и 3, а стержень 1 работает еще в упругой стадии (рис. 83.6, б). Проводим ось а–а, перпендикулярную направлению нормальной силы N₁. Проектируем все силы на эту ось: и определяем

Второй механизм разрушения. Пусть текут стержни 1 и 3, а стержень 2 работает в упругой стадии (рис.83.6, в). Проводим ось б–б, перпендикулярную направлению оси стержня 2. Проектируем все силы на эту ось:

и находим

При возникновении второго механизма разрушения стержень 2 будет вращаться вокруг шарнира А (рис.83.6, а), следовательно, стержень 1 будет растягиваться, а стержень 3 сжиматься (рис.83.6, в). В этом случае полагаем, что N_u₃ = 0, т.е. его влияние идет в запас прочности конструкции, так как предполагаем, что сжатый стержень теряет устойчивость и в нем нормальные напряжения не достигают значения предела текучести.

Третий механизм разрушения. Пусть текут стержни 1 и 2, а стержень 3 работает в упругой стадии (рис.83.6, г). Проводим ось в–в, перпендикулярную направлению оси стержня 3. Проектируем все силы на эту ось:

откуда

Истинное значение предельной нагрузки будет наименьшим из полученных трех нагрузок F_u₁, F_u₂, F_u₃:

83.4. Предельное состояние статически определимых систем при кручении

Предельным состоянием для идеально пластического материала будет такое, при котором касательные напряжения во всех точках поперечного сечения станут равными пределу текучести (рис. 83.7).

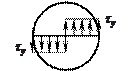
Рис.83.7

При упругом кручении круглого стержня максимальные касательные напряжения в контурных точках определяют по формуле Выражение для предельного крутящего момента как результирующего момента, возникающего в поперечном сечении (рис. 83.7) от внутренних касательных напряжений , имеет вид

где W_p_,_pl – пластический момент сопротивления при кручении, который для сплошного круглого поперечного сечения вычисляется по формуле

а для кольцевого сечения с наружным D и внутренним d диаметрами по формуле

где .

Пример 5.

Стальной стержень сплошного круглого сечения диаметром d = 5 см, жестко закрепленный с обоих концов, нагружен крутящим моментом М_u (рис.83.8, а). Определить предельный крутящий момент, если предел текучести материала стержня при кручении =150 МПа.

Рис.83.8

Решение.

В предельном состоянии в поперечных сечениях стержня возникают предельные крутящие моменты Т_u, равные

Выделим часть стержня сечениями I–I и II–II (рис. 83.8, б). На оставшуюся часть стержня в предельном состоянии кроме момента M_u действуют моменты T_u, приложенные по торцам оставшегося участка и направленные в сторону, противоположную M_u. Составим уравнение равновесия:

или M_u = 2T_u.

Окончательно величина предельного внешнего крутящего момента будет M_u = 2T_u =2∙4,91= 9,82 кНм.

83.5. Предельное состояние статически определимых систем при изгибе

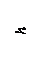
Подпись: h

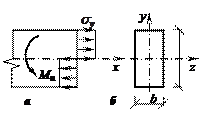
Рис.83.9

Напряженное состояние изгибаемых конструкций (балок) определяется величинами изгибающих моментов. При плоском поперечном изгибе изгибающий момент, не может быть больше момента текучести:

или

где и – соответственно статические моменты верхнего и нижнего полусечения относительно нейтральной оси z; W_z_,_pl – пластический момент сопротивления.

Например, для прямоугольного поперечного сечения (рис. 83.9, а, б):

В балках при достижении наибольшими изгибающими моментами значений M_u образуются пластические шарниры (рис. 83.9, а). В этом случае изгибающий момент в сечении равен предельному M_u и не может увеличиваться, а деформирование балки далее происходит при постоянном значении изгибающего момента в пластическом шарнире.

Статически определимая балка имеет предельную нагрузку соответствующую образованию пластического шарнира в наиболее напряженном сечении, когда балка превращается в механизм.

Статически неопределимая стержневая система или балка при разрушении тоже превращается в механизм. При этом в балках или рамах необходимо образование стольких пластических шарниров, сколько требуется для превращения их в механизм.

Пример 6.

Дана стальная однопролетная шарнирно опертая балка, нагруженная по всему пролету равномерно распределенной нагрузкой q = 20 кН/м, расстояние между опорами l = 3 м. Подобрать сечение прокатной двутавровой балки, если R_y= 240 МПа, γ_c = 1, и определить, во сколько раз необходимо увеличить равномерно распределенную нагрузку q, чтобы в балке образовался пластический шарнир. Принять предел текучести стали R_yn = 285 МПа. Собственным весом балки пренебречь.

Решение.

Определяем максимальный изгибающий момент в середине пролета балки:

Находим необходимый момент сопротивления поперечного сечения балки:

По сортаменту выбираем двутавр № 16 с W_z= 109 см³ и статическим моментом площади полусечения относительно нейтральной оси z – = = 62,3 см³.

По формуле находим момент текучести

И, наконец, определяем n = M_u/ M_max = 35,51/22,5 = 1,58.

Следовательно, если равномерно распределенную нагрузку q =20 кН/м увеличить в 1,58 раза, то в середине пролета в поперечном сечении балки возникнет пластический шарнир и балка превратится в механизм.

Пример 7.

Рассмотрим предельное состояние балки с двумя шарнирно опертыми концами, от действия силы P, приложенной в середине пролета. В статически определимой балке (рис.83.10), как известно, нормальные напряжения в поперечных сечениях в упругой стадии, изменяются по высоте сечения по линейному закону и пропорциональны величине изгибающего момента.

В опасном сечении при достижении напряжений в крайних волокнах величины , заканчивается упругий стадия работы и величина изгибающего момента по теории допускаемых напряжений будет определяться следующими известными соотношениями:

откуда допускаемое значение внешней силы вычисляется по:

где W - момент сопротивления поперечного сечения балки. Для прямоугольного сечения где b, h - размеры поперечного сечения (рис.83.10, б).

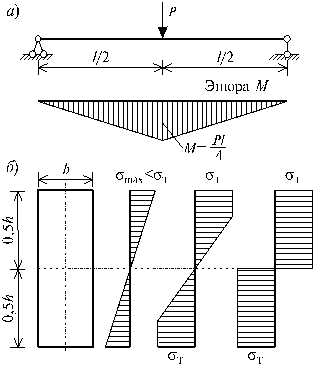
Рис. 83.10

Таким образом, при расчете балки (рис.83.10, а) по теории допускаемых напряжений, допускаемое значение внешней силы, определяется по:

Однако, очевидно, что при P=P_доп, вычисленной по формуле (83.30), заданная балка далеко не исчерпала свою несущую способность. При увеличении нагрузки, пластические деформации проникают вглубь сечения, вплоть до появления в нем пластического шарнира, т.е. состояния сечения, при котором все ее точки перешли в пластическое состояние. В пластическом шарнире момент достигает предельной величины, когда эпюра нормальных напряжений во всех точках в опасном сечении принимает значение (рис.83.10, б).

Согласно диаграмме деформирования материала по Прандтлю, продольные волокна балки в этом сечении испытывают беспредельно возрастающие деформации. В этих условиях можно говорить о формировании пластического шарнира в сечении, который превращает данную балку в механизм (рис.83.11). Это означает, что с возникновением пластического шарнира происходит полное исчерпание несущей способности балки, т.е. заданная система разрушается. Величину силы, вызывающую образование в балке пластического шарнира, называют предельной силой метода предельного состояния.

Рис. 83.11

Значение предельной силы определяется из условия равенства моментов внутренних и внешних сил для опасного срединного сечения балки:

откуда получим:

Величина называется пластическим моментом сопротивления.

Если сравнить величину предельной силы, определенной по методу допускаемых напряжений и по методу предельного равновесия, то получим, что

Из приведенного примера следует, что для расчета изгибаемых элементов по методу предельного состояния, необходимо предварительно определить пластический момент сопротивления в сечениях пластических шарниров.

В таблице 83.1 приведены значения отношения для некоторых стандартных форм сечений.

Таблица 83.1

Форма сечения
	1,16	1,27	1,50	1,70	2,00

83.6. Расчет статически неопределимых балок по предельному состоянию.

Кинематический и статический способ

При расчете статически определимой балки было установлено, что ее несущая способность исчерпается, когда, хотя бы в одном, т.е. в наиболее опасном сечении пластическая область заполняет все сечение, т.е. когда в этом сечении образуется пластический шарнир и система становится геометрически изменяемой.

Для статически неопределимых балок образование одного пластического шарнира не приводит к исчерпанию несущей способности, т.к. в этом случае степень кинематической определимости системы снижается на одну единицу. В случае n раз статически неопределимой балки исчерпание несущей способности происходит при формировании n + 1 пластических шарниров. Однако в ряде случаев часть балки может стать геометрически изменяемой при значительно меньшем числе пластических шарниров.

Например, в статически многократно неопределимой балке с консолью (рис.83.12), несущая способность заданной системы исчерпается в случае возникновения первого же пластического шарнира над крайней правой опорой.

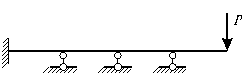
Рис. 83.12

Для расчета статически неопределимых систем по теории предельного равновесия можно воспользоваться одним из двух способов - кинематическим или статическим.

При применении кинематического способа, в предельном состоянии составляется уравнение работы всех внешних и внутренних усилий на основе принципа возможных перемещений. Этот принцип формулируется так: если система твердых тел находится в равновесии под действием системы сил, то работа, совершаемая этими силами на любом малом возможном перемещении системы, должна быть равна нулю.

При применении статического способа при отсутствии упругого расчета, на основе которого, предварительно можно определить наиболее вероятную схему разрушения конструкции, задаются различные схемы разрушения предельной стадии работы рассматриваемой системы, и для каждой из них составляются уравнения равновесия и определяются предельные значения внешних сил. Из их числа, наименьшая является расчетной величиной предельной силы.

Из числа рассмотренных схем разрушения, на основании которых определяется предельная сила, является наиболее вероятной схемой, разрушения конструкции.

Рассмотрим несколько характерных примеров для определения предельной нагрузки для статически неопределимых балок, принимая диаграмму растяжения-сжатия материалов без упрочнения, т.е. диаграмму Прандтля.

Пример 8.

Пусть трехопорная балка (рис.83.13, а) нагружена силой величиной Р. Эта балка один раз статически неопределимая. На рис.83.13, б изображена эпюра изгибающих моментов, при упругой стадии деформирования. Для решения этой задачи применим статический способ.

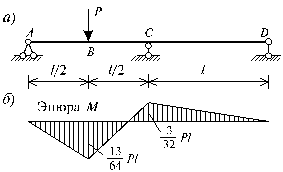
Рис. 83.13

Значение силы , при которой в наиболее опасной точке балки напряжение достигает предела текучести, и может быть установлено из равенства наибольшего момента, действующего в опасном сечении, допускаемому . Откуда, получим:

Если балка имеет прямоугольное поперечное сечение, то

и, следовательно,

Наращивая величину внешней силы , пластическая область в опасном сечении В балки увеличивается. При некотором значении силы в сечении В возникает пластический шарнир, тогда величина изгибающего момента в этом сечении становится равной . При дальнейшем росте внешней силы Р, момент в сечении В остается постоянным и равным . Это означает, что трехопорная балка приобретает пластический шарнир в т. В. При этом она нагружена силой Р и двумя моментами , приложенных в разных торцах сечения В (рис.83.14, а). Следовательно, в данном случае возникновение одного пластического шарнира превращает один раз статически неопределимую балку в балку статически определимую.

Рис. 83.14

При дальнейшем росте силы Р изгибающие моменты в сечении В и на участке АВ не возрастают, а изгибающие моменты на участке ВСD, с ростом величины силы Р, растут. При указанных предположениях, наибольшая величина изгибающего момента формируется в сечении С, где он раньше всего и достигает предельной величины .

Когда в сечении С изгибающий момент достигнет предельной величины , т.е. когда в этом сечении сформируется пластический шарнир, несущая способность балки исчерпается, вследствие чего, балка превращается в геометрически изменяемую систему.

Согласно статическому способу, и учитывая, что наиболее вероятная схема разрушения конструкции очевидна и изображена на рис.83.14, б, величина предельной силы определяется из уравнений равновесия и условий равенства изгибающего момента в сечениях пластического шарнира предельному моменту :

Решая совместно последнюю систему уравнений, получим:

откуда:

При расчете по методу допускаемых напряжений расчетная величина допускаемой силы определяется:

где n - коэффициент запаса по несущей способности конструкции.

В случае расчета по методу предельных состояний, величина допускаемой силы, принимает значение:

Сопоставляя выражения (83.36) и (83.37), получим, что метод расчета по предельному состоянию дает величину допускаемой силы в 117/64≈1,83 раза больше, чем метод расчета по допускаемым напряжениям, при условии, что коэффициент запаса в обоих методах принят одинаковым.

В заключении рассмотрим балку с одним защемленным, а вторым шарнирно опертым концами, нагруженной двумя одинаковыми силами (рис.83.15, а).

Рис. 83.15

Определим величину предельной силы кинематическим способом, предложенным А.А.Гвоздевым.

Рассматриваемая балка, один раз статически неопределима и, следовательно, ее несущая способность исчерпается в случае образования двух пластических шарниров.

Пластические шарниры могут формироваться в сечениях А, В и С. Для определения предельной нагрузки по кинематическому способу А.А.Гвоздева необходимо рассмотреть различные сочетания образования пластических шарниров в двух сечениях из трех. Число таких комбинаций равно трем, т.е. числу сочетаний из трех пластических шарниров по два.

Для различных вариантов расположения пластических шарниров составляются уравнения равновесия, при условии равенства изгибающего момента в сечениях пластического шарнира предельному моменту . Из полученных уравнений могут быть определены величины предельных нагрузок. Действительной предельной нагрузкой будет наименьшая из вычисленных для различных сочетаний пластических шарниров.

Необходимо заметить, что при составлении уравнений предельного равновесия системы, можно использовать из трех уравнений статического равновесия всей системы в целом, только два из них. Третье уравнение автоматически будет удовлетворяться. Недостающие уравнения могут быть получены, из рассмотрения равновесия отсеченной части системы, предполагая, что рассматриваемое сечение проходит через пластический шарнир.

Рассмотрим различные возможные схемы предельной стадии работы конструкции.

Первая схема, предполагая, что пластические шарниры формируются в сечениях А и В (рис.83.15, б):

Откуда

Вторая схема, предполагая, что пластические шарниры формируются в сечениях А и С (рис.83.15, в):

Откуда

Третья схема, предполагая, что пластические шарниры формируются в сечениях В и С (рис.83.15, г):

откуда, решая совместно эту систему уравнений, получим значения изгибающего момента в заделке и значение предельной нагрузки :

Так как условие не может быть реализовано, то третью схему следует исключить из дальнейшего рассмотрения.

Сопоставляя предельные значения внешней силы, приведенные в (83.38)-(83.39), определяем, что наименьшая предельная нагрузка имеет место при второй схеме предельного равновесия, т.е. когда пластические шарниры формируются в сечениях А и С:

Далее рассмотрим применение кинематического способа - метода предельных состояний для определения величин продольных сил. Действительная схема разрушения системы показана на рис.83.16. Составим уравнения работ всех внутренних и внешних усилий на возможных перемещениях:

Составляя уравнения совместности, получим:

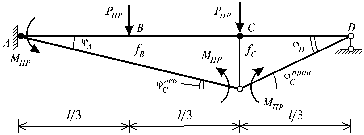
Рис. 83.16

Уравнение (83.41), с учетом (83.42), примет вид:

Откуда

Сопоставляя выражения (83.43) и (83.39), заметим, что кинематический и статический способы дали идентичные результаты по значению предельной силы.

Пример 9.

Для статически неопределимой балки (рис.83.17, а) по методу предельного равновесного состояния и по методу допускаемых напряжений определить расчетную величину внешней силы P и сравнить полученные результаты, предполагая, что балка имеет постоянное поперечное сечение прямоугольной формы с размерами b×h.

Решение.

Сначала рассмотрим расчет заданной системы по методу допускаемых напряжений.

Заданная система один раз статически неопределима. Для определения положения опасного сечения и величины изгибающего момента в опасном сечении в упругой стадии работы балки применим метод сил.

Основная система представлена на рис.83.17, б. На рис.83.17, в и рис.83.17, г в основной системе изображены эпюры моментов от силы X = 1 и P. Далее, по формуле Мора вычисляем коэффициенты канонического уравнения:

Из решения канонического уравнения метода сил:

получим:

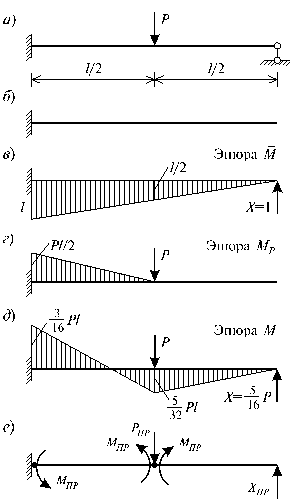
Рис. 83.17

После определения величины опорной реакции Х, построим окончательную эпюру моментов в заданной системе (рис.83.17, д). Откуда следует, что опасным является сечение 1, где значение момента равно

Предполагая, что в опасном сечении в опасной точке напряжение равно по методу допускаемых напряжений определим допускаемую величину внешней силы P=P_доп:

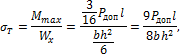
откуда

Для расчета заданной системы по методу предельного равновесного состояния, предварительно выразим значения моментов в сечениях 1 и 2 через внешнюю силу P и реакции X возникающей в месте шарнирного опирания:

Исключая опорную реакцию Х из последних соотношений, получим:

Учитывая, что в предельном состоянии, в данном случае, имеем: ; ; , уравнение (83.45) преобразуется в виде:

откуда окончательно получим:

Принимая во внимание результаты расчетов по методу допускаемых напряжений и по методу предельного равновесия, соответственно (83.44) и (83.46), составим отношение:

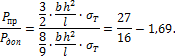
Следовательно,

т.е. несущая способность рассматриваемой системы по результатам расчетов метода предельного равновесия в 1,69 раза больше, нежели по методу допускаемых напряжений.

Пример 10.

Дана статически неопределимая балка постоянного прямоугольного поперечного сечения (рис. 83.18, а). Определить предельную нагрузку F_u, если предел текучести материала балки = 285 МПа.

Рис. 83.18

Решение.

Определяем предельный изгибающий момент (момент текучести), используя формулы и :

Для балки, нагруженной сосредоточенными силами, эпюра изгибающих моментов изображается ломаной линией (рис. 83.18, б). Пики эпюры моментов будут находиться в заделке и в точках приложения сосредоточенных сил. В этих сечениях и могут возникать пластические шарниры. В рассматриваемом случае возможны два механизма разрушения балки.

Первый механизм разрушения. Предположим, что пластические шарниры образовались в заделке и в сечении на расстоянии l₁= 3 м от заделки (рис. 83.18, в).

Составим уравнение предельного равновесия для всей балки (рис. 83.18, в):

и для правой части балки (рис. 83.18, г):

В результате получена система двух уравнений с двумя неизвестными величинами F_u₁ и V_B₁:

решая которую находим первое значение предельной нагрузки F_u₁ :

Второй механизм разрушения возможен при возникновении пластических шарниров в заделке и в сечении на расстоянии l₃= 3 м от правой опоры (рис. 83.18, д).

Составим уравнение предельного равновесия для всей балки (рис. 83.18, д):

и для правой части балки (рис. 83.18, е):

В результате получена система двух уравнений с двумя неизвестными величинами F_u₂ и V_B₂:

решая которую находим второе значение предельной нагрузки F_u₂:

Истинным значением предельной нагрузки должно быть наименьшее из F_u₁ и F_u₂, но в нашем случае обе предельные нагрузки равны, следовательно,

Пример 11.

Пусть дана однопролетная балка, нагруженная двумя сосредоточенными силами (рис. 83.19). Материал балки – сталь с пределом текучести = 285 МПа. Балка имеет прямоугольное поперечное сечение =. Требуется определить предельную нагрузку F_u.

Эта задача была решена в примере 10 методом, определяемым статическими теоремами теории предельного равновесия. Решим эту же задачу методом, определяемым кинематическими теоремами теории предельного равновесия. В этом случае будут использоваться формулы для определения работ W внутренних и внешних сил F и моментов М:

W=F∆ и W=MΘ, (83.47)

где ∆ – путь, пройденный силой F; Θ – угол поворота сечения.

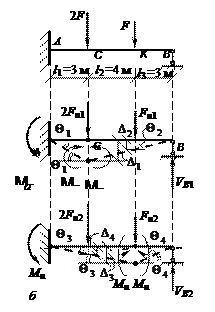
Рис. 83.19

Решение.

Первый механизм разрушения образуется при возникновении пластических шарниров в сечениях А и С. Составим уравнение равенства работ внешних и внутренних усилий:

Учитывая малость углов, запишем (рис. 83.19, а):

откуда далее ; откуда

Из подобия треугольников (рис. 83.19, а) определяем:

откуда .

Полученные выражения подставим в уравнение равенства работ (83.48):

откуда и определяем предельную нагрузку F_u₁ для первого варианта разрушения балки (рис.20.19, а):

Полученный результат совпал с результатом, полученным в примере 10.

Рассмотрим второй возможный механизм разрушения балки. Он будет при возникновении пластических шарниров в сечениях А и К (рис. 83.19, б).

Составим уравнение равенства работ внешних и внутренних сил:

Согласно рис.83.19, б с учетом малости углов запишем

Откуда

Из подобия треугольников (рис. 83.19, б) определяем

Полученные выражения для , , подставим в уравнение работ (20.49) для второго возможного механизма

откуда и находим предельную нагрузку F_u₂:

Окончательно получаем: F_u = min{F_u₁, F_u₂}= min{95; 95}= 95 кН.

Вопросы для самопроверки

- Поясните суть метода допускаемых напряжений.

- Поясните суть метода предельного равновесного состояния.

- Перечислите теории пластичности и дайте соответствующие пояснения.

- Перечислите основные гипотезы, взятые за основу деформационной теории пластичности.

- Поясните суть кинематического метода предельного равновесного состояния.

- Поясните суть статического метода предельного равновесного состояния.

- Дайте определение понятия пластического шарнира при изгибе конструкций.

- В чем заключается различие между расчетами на прочность по допускаемому напряжению и по предельным нагрузкам?

- Что представляет собой предельная нагрузка?

- Почему при расчете по предельным нагрузкам нельзя использовать формулы, основанные на законе Гука?

- В чем заключается схематизация диаграмм растяжения?

- Почему расчет по предельным нагрузкам выполняют только для элементов конструкции из пластичных материалов?

- Какой вид имеют эпюры напряжений в поперечных сечениях бруса при кручении или изгибе при предельных значениях крутящих или изгибающих моментов?

- Что представляет собой пластический шарнир?

- Как определить предельный изгибающий момент?

- Как определить предельный крутящий момент?

- Почему расчеты статически определимых стержней при растяжении и сжатии по допускаемым напряжениям и предельным нагрузкам дают одинаковые результаты?

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00