Главная
Часть
9. Расчет статически неопределимых стержневых систем методом конечных элементов
9.1.
Общие понятия и классификация задач вычислительной механики
Механика как фундаментальная научная дисциплина может быть подразделена на три основные части:

Теоретическая механика имеет дело с фундаментальными законами и принципами, описывающими механическое движение абсолютно твердых и деформируемых тел. Прикладная механика на основе теорем теоретической механики занимается построением математических моделей физических явлений, формулировкой и решением научно-исследовательских и инженерных задач. Вычислительная механика решает специфические задачи путем математического моделирования с помощью численных методов, реализованных на цифровых вычислительных машинах.
ЗАМЕЧАНИЕ
Перефразирую старую шутку о математиках, можно определить механика-расчетчика, как человека, который ищет решения заданных задач; механика-прикладника, как человека, который ищет практические задачи, соответствующие данным решениям; и механика-теоретика, как человека, который доказывает существование задач и их решений.
9.1.1.
Вычислительная механика
Области приложений вычислительной механики могут быть выделены в соответствии с физическим масштабом решаемых задач.
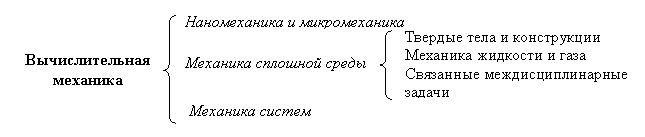
Наномеханика имеет дело с явлениями на молекулярном и атомном уровнях материи и, таким образом, тесно взаимодействует с физикой частиц и химией. Микромеханика в основном рассматривает явления на уровне кристаллов и гранул. Ее основное технологическое приложение – дизайн и производство материалов и микроприборов.
Механика сплошной среды изучает тела на макроскопическом уровне, используя континуальные модели, в которых микроструктура гомогенизируется с помощью феноменологического подхода. Две традиционные области приложения механики сплошной среды – механика жидких и твердых тел; последняя включает механику конструкций, которые, очевидно, изготавливаются из твердых тел. Вычислительная механика твердого тела использует научно-прикладной подход, в то время как вычислительная механика конструкций акцентирует внимание на технологических приложениях к анализу и дизайну конструкций.
Вычислительная механика жидкостей имеет дело с задачами, описывающими равновесие и движение жидкости и газов, включая такие хорошо разработанные области как гидродинамику, аэродинамику, физику атмосферы, физику горения и взрыва.
Механика связанных задач - одна из последних областей приложения численных методов. Подразумевается, что эта область включает физические системы, выходящие за классические границы механики твердых и жидких тел, рассматривает взаимодействие жидкостей и конструкций. Например, фазовые задачи, такие как таяние льда или застывание металла, соответствуют данной категории, поскольку включают взаимодействие механических и электромагнитных явлений.
Наконец, механика систем имеет дело с механическими объектами, естественными или искусственными, проявляющими характерные макроскопические функции. Пример искусственных систем – самолеты, дома, мосты, двигатели, машины, микрочипы, роботы и т.д.; биологических систем – целые животные или деревья, изучаемые с позиций биомеханики. В выше рассмотренной схеме системы представляют собой наиболее общую концепцию, изучаются они путем декомпозиции: поведение отдельных компонент системы плюс взаимодействие между компонентами. В свою очередь компоненты могут быть разложены на более мелкие части и т.д. Продолжая этот иерархический процесс можно получить отдельные компоненты достаточно простые для того, чтобы быть изученными в рамках отдельных дисциплин. Однако взаимодействие между ними может оказаться гораздо более сложным. Соответственно, искусство исследователя состоит в том, чтобы правильно определить, на каком иерархическом уровне системы необходимо остановиться для того, чтобы получить нетривиальный результат.
9.1.2.
Статика и динамика
Задачи механики сплошной среды могут быть классифицированы в соответствии с тем, принимается во внимание эффект инерции или нет:
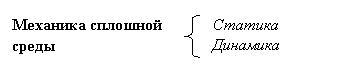
В динамике явно рассматривается зависимость от времени, поскольку вычисление сил инерции (а так же, возможно, демпфирующих сил) требует вычисление производных по времени.
Задачи статики так же могут быть временно зависимыми, однако, силами инерции пренебрегают в силу их малости. Статические задачи могут быть так же подразделены на строго статические и квази-статические. В математическую формулировку последних время явно не входит; вместо него в случае необходимости используются временно подобный параметр, характеризующий историю процесса. В других квази-статических задачах, таких как расчет деформации ползучести, циклическая усталость, пластичность, зависящая от скорости нагружения, требуется более реалистичная оценка времени, однако, и в этом случае инерциальные силы пренебрежимо малы.
9.1.3.
Линейность и нелинейность
Задачи механики могут быть так же подразделены на линейные и нелинейные:
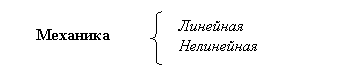
Линейная механика имеет дело с проблемами, в которых отклик системы линеен в причинно-следственном смысле. Например, если приложенные внешние силы удваиваются, то результирующие перемещения и внутренние напряжения так же удваиваются. В противоположном случае задачи классифицируются как нелинейные.
9.1.4.
Численные методы строительной механики
Строительная механика на современном этапе развития располагает большим арсеналом методов расчета как дискретных систем (например, состоящих из стержней), так и континуальных (сплошных) конструкций и их элементов, таких как пластины, плиты, оболочки, массивы.
Расчет напряженно-деформированного состояния дискретной конструкции, как правило, приводит непосредственно к решению систем алгебраических уравнений. Пример этому – широко применяемые при расчете плоских и пространственных стержневых систем классические методы сил и перемещений.
Для расчета континуальных систем используются более сложные математические модели и соответственно численные методы. Так, основные зависимости между геометрическими и физическими величинами в механике сплошных сред выводятся с помощью элемента бесконечно малых размеров. Соотношения между средними значениями этих величин, предполагая их непрерывность, распространяются с бесконечно малых элементов на всю рассматриваемую область. Таким образом, появляются дифференциальные, интегральные или интегро-дифференциальные уравнения, вместе с граничными и начальными условиями они образуют математическую модель соответствующей задачи. К сожалению, точное решение в аналитической форме прикладных континуальных задач возможно лишь в очень немногих случаях, поэтому особо важное значение приобретают приближенные, но достаточно общие методы их решения. В последние десятилетия эти методы, называемые также численными, получили особенно активное развитие в связи с применением в инженерной практике современных вычислительных средств.
В основе почти всех современных численных методов лежит аппроксимация дифференциальных и интегральных уравнений, а также граничных условий конечным числом (т. е. системой) алгебраических уравнений относительно дискретных неизвестных – обычно это значения искомой функции в дискретных точках. Такое сведение континуальной задачи к дискретной равносильно замене сплошной конструкции с бесконечным числом степеней свободы на приближенную дискретную модель с конечным числом степеней свободы.
К настоящему времени известно значительное число разнообразных приближенных методов. При этом различные методы применяются для решения дифференциальных и интегральных уравнений, вариационных задач. Общим недостатком большинства из них является то, что они разрабатывались для решения определенного класса задач механики деформируемого тела и таким образом не являются универсальными. К тому же для исследования массивов сложной формы, комбинированных систем, многих других конструкций использование ряда методов неэффективно и даже неприемлемо.
Оценивая тот или иной численный метод, основное внимание необходимо уделять таким качествам, как универсальность, точность аппроксимации, простота алгоритма, объем вычислений и т. п. Для проведения практических расчетов нужно выбирать достаточно надежные методы, обладающие хорошей сходимостью и опробованные на большом количестве разнообразных задач. Этим требованиям отвечают метод конечных разностей (МКР), вариационно-разностный метод (ВРМ), метод конечных элементов (МКЭ). Причем в рамках каждого из этих методов разработано множество направлений и модификаций, оправдывающих себя при решении различных классов задач.
В настоящее время в линейной механике твердого тела метод конечных элементов наиболее распространен, в то время как применение метода граничных элементов для решения данных задач находится на втором месте. Для нелинейных задач метод конечных элементов является наиболее эффективным и доминирующим.
Классический метод конечных разностей почти полностью потерял свое значение при решении практических задач механики твердого тела. Это утверждение, однако, не верно для механики жидкости и газов, где разностные методы до сих пор широко распространены. Метод конечных объемов, основанный на законах сохранения, применяется для решения сильно нелинейных задач механики жидкости и газов. Спектральные методы используются в различных областях механики и основаны на пространственно-временном преобразовании в область, где задача может быть легко решена. Метод свободных сеток – один из новых методов вычислительной математики и основан на конечно-разностном подходе с использованием независимых сеток, полученных в результате применения конечно-элементных технологий.
Следующие параграфы этой главы знакомят читателя с указанными приближенными методами на примере простейших одномерных задач, доступных для студентов строительных специальностей. Однако из этого не следует, что эти методы предназначены для решения столь простых задач, ибо применение универсальных методов к одномерным системам вообще не является эффективным. На этих примерах прослеживается последовательность стандартных действий, составляющая алгоритм решения и иллюстрирующая характерные особенности того или иного метода. Без особых изменений приведенные схемы могут быть использованы при решении существенно более сложных двумерных и трехмерных задач.
9.1.5.
Варианты метода конечных элементов (МКЭ)
Термин Метод Конечных Элементов в действительности определяет широкий спектр вычислительных технологий в соответствии с некоторыми общими свойствами, которые будут рассмотрены в дальнейшем. Классификация МКЭ применительно к механике конструкций в зависимости от типа искомой функции может быть представлена следующим образом:
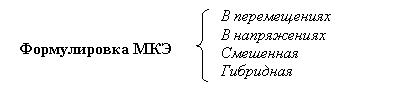
Различие между этими формулировками проистекает из вида вариационного принципа, используемого для построения алгоритма МКЭ, и, соответственно, из вида искомой функции:

9.1.6.
Процесс конечно-элементного анализа
Процесс конечно-элементного анализа включает определенную последовательность шагов. Эта последовательность имеет две канонические конфигурации в зависимости от окружения, в котором используется МКЭ:
Математический подход
Физический подход.
Схема математического подхода изображена на рис. 9.1. В центре данного подхода находится математическая модель. Обычно это есть обыкновенное дифференциальное уравнение или уравнение в частных производных по пространственным координатам и времени. Дискретная конечно-элементная модель генерируется путем применения какого-либо вариационного принципа к исходной системе дифференциальных уравнений или же метода взвешенных невязок в его ослабленном варианте. Этот шаг называется дискретизацией. Получаемая система конечно-элементных уравнений решается одним из методов прикладной математики решения больших систем алгебраических уравнений. В результате чего получается так называемое дискретное, или приближенное, решение.
Идеальная физическая система в данном случае может быть представлена как реализация математической модели; и наоборот, математическая модель есть идеализация этой системы. Например, если математическая модель есть уравнение Пуассона, то его реализацией может быть проблема распределения электростатического заряда или распределение тепла. В принципе этот шаг не существенен и может быть опущен. Другими словами, конечно-элементная дискретизация может быть приведена и без обращения к физике явления.
Концепция ошибки, или погрешности, возникает, когда приближенное решение подставляется в математическую модель. Эта подстановка называется верификацией. Полная ошибка численного подхода включает в себя ошибку решения системы алгебраических уравнений и погрешность дискретизации. Подстановка приближенного решения в идеальную физическую систему, т.е. проведение теста или опыта, в принципе могла бы дать оценку этой ошибки моделирования. Однако, в концепции математического подхода МКЭ физическая система не играет большой роли и является лишь некоторым идеализированным образом математической модели.
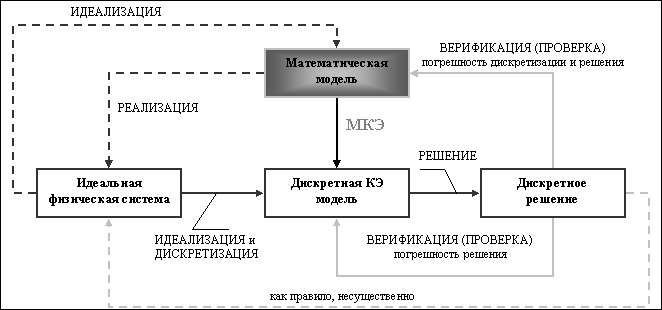
Рис. 9.1. Математическая концепция МКЭ
Схема физического подхода изображена на рис. 9.2. Центральным звеном в этом случае является физическая система, которая должна быть рассчитана. Процедуры идеализации и конечно-элементной дискретизации проводятся одновременно, чтобы получить дискретную модель. Приближенное дискретное решение получают аналогично предыдущему.
Идеальная математическая модель в данном подходе может быть представлена как предельный переход или «континуализация» дискретной модели. Для определенных физических систем, которые хорошо моделируются непрерывными полями, этот шаг существенен, для других, таких как сложные инженерные системы, подобный переход не имеет большого смысла. Для них конечно-элементная модель может быть построена без обращения к математическим моделям только на основе экспериментальных измерений.
Понятие погрешности, или ошибки, возникает в физическом подходе благодаря двум процедурам – верификации численного решения и оценки результатов моделирования (ратификации). Верификация имеет тот же смысл, что и в математическом подходе: численное решение подставляется в дискретную модель, в результате чего получается погрешность решения. Подстановка приближенного решения в идеальную математическую модель, в принципе, может дать ошибку дискретизации. Однако это редко используется в сложных инженерных системах, поскольку, как правило, в данном случае математической модели не существует, и сравнивать полученное решение необходимо с исходной физической системой. Таким образом, оценка или ратификация численного решения основана на сравнении результатов моделирования с экспериментальными данными, что и дает суммарную погрешность моделирования.
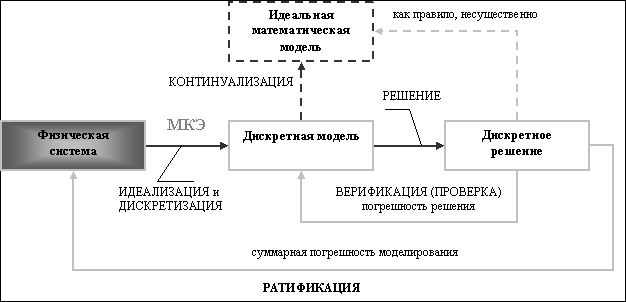
Рис.9.2. Физическая концепция МКЭ.
Один из способов настройки дискретной модели, для того чтобы она лучше соответствовала физической системе, называется уточнением модели (Рис.9.3). Имеющиеся свободные параметры модели определяются путем сравнения дискретного приближенного решения с результатами эксперимента, как показано на рис.9.3. Поскольку, условия минимизации ошибки моделирования, как правило, нелинейные (даже если конечно-элементная модель линейная), то процесс уточнения является существенно итерационным.
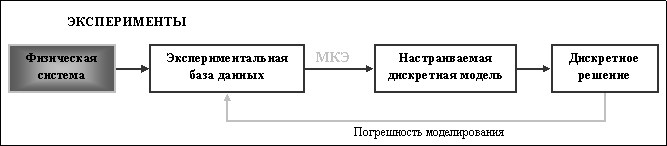
Рис. 9.3. Процесс уточнения дискретной модели.
Выше рассмотренные подходы применения МКЭ не являются взаимоисключающими, а дополняют друг друга. Исторически физический подход был первым для разработки конечно-элементных моделей очень сложных инженерных систем, таких как самолеты, корабли и т.п. Математический подход возник позднее и среди прочих вещей призван обеспечить необходимый теоретический фундамент МКЭ, для того чтобы распространить метод на решение различных междисциплинарных задач выходящих за рамки общепринятого прочностного анализа конструкций.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21