Главная

9.7. Постановка плоской задачи теории упругости методами МКЭ

9.7.1. Основные понятия

Плоская задача теории упругости является наиболее подходящим примером для демонстрации алгоритма МКЭ применительно к решению многомерных задач механики сплошных сред. Базовые соотношения и особенности алгоритма метода конечных элементов в данном случае существенно отличаются от расчета одномерных задач (растяжения, кручения и изгибы стержней).

В механике конструкций плоский тонкий лист материала называется пластиной. Расстояние между верхней и нижней поверхностью пластины называется толщиной и обозначается через h. Пластина имеет также срединную плоскость, лежащую между двух поверхностей. Направление перпендикулярное срединной плоскости называется трансверсальным. Как правило, глобальная ось z направлена перпендикулярно срединной плоскости, в то время как оси x и y лежат в срединной плоскости, образуя глобальную декартову систему координат (Рис. 9.49). Таким образом, уравнение срединной плоскости имеет вид: z=0.

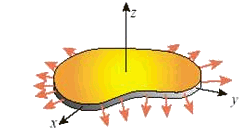
Рис. 9.49. Двумерная конструкция в плоско-напряженном состоянии.

Для того чтобы пластина находилась в плоско-напряженном состоянии, необходимо чтобы выполнялись следующие условия:

Все внешние нагрузки: поверхностные, действующие на точки боковой поверхности пластины, и объемные, действующие на внутренние точки пластины, - перпендикулярны оси z, т.е. лежат в плоскости xy, и симметричны относительно срединной плоскости.

Все условия закрепления симметричны относительно срединной плоскости.

Внутренние перемещения, деформации и напряжения принимаются постоянными по толщине пластины.

Нормальные и сдвиговые компоненты тензора напряжений в направлении оси z равны нулю или пренебрежимо малы.

Пластина изготовлена из материала, не меняющего своих свойств по толщине. Такие пластины называются трансверсально-однородными.

Заметим, что 3 и 4 предположения не являются необходимым следствием первых двух. Чтобы они выполнялись толщина h должна быть достаточно малой, обычно не более 10% наименьшего характерного размера пластины в срединной плоскости. Кроме того, если толщина пластины изменяется, то это изменение должно быть достаточно плавным. И, наконец, геометрия пластины должна быть симметричной относительно срединной плоскости.

Последнее предположение очевидно исключает из рассмотрения плоские композиционные конструкции, типа ячеистых сотоподобных структур или сендвич-структур. Разработка моделей таких конструкций требует достаточно сложного интегрирования по толщине пластины, а также учета эффектов изгиба и растяжения, и в данном курсе рассматриваться не будет.

Замечание 1. Нагрузка перпендикулярная срединной плоскости приводит к напряженному состоянию, называемому изгибом пластины, описываемому дифференциальным уравнением IV-го порядка относительно прогиба пластины. Алгоритм МКЭ в этом случае имеет принципиально иной характер, поскольку данная задача относится к классу одномерных задач.

Замечание 2. Если принято, что напряжения вдоль оси z имеют место, то состояние пластины носит название обобщенного плоско-напряженного состояния.

Замечание 3. Кроме плоско-напряженного состояния в теории упругости широко применяется понятие плоско-деформированного состояния, согласно которому деформация вдоль оси z равна нулю. Физически это соответствует протяженным конструкциям, нагруженным силами перпендикулярно оси z. Например, плотина, дамба или лопатка ротора генератора при некоторых допущениях.

9.7.2. Математическая модель

Математическая модель пластины в плоско-напряженном состоянии есть двумерная краевая задача теории упругости, заданная в области с границей Г, как показано на рис. 9.50.

Все основные переменные, входящие в исходные уравнения, представляют собой функции двух переменных x и y и считаются осредненными по толщине пластины. Например, внешние силы, действующие в области и входящие в правую часть уравнения движения точек сплошной среды, есть не что иное, как интегралы по толщине пластины от заданных объемных сил.

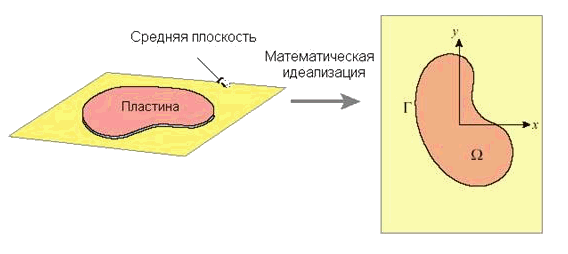
Рис. 9.50. Математическая модель пластины в плоско-напряженном состоянии.

9.7.3. Исходные данные

Исходные данные включают в себя следующие объекты:

Геометрия области. Геометрия тела представляет собой область с границей Г, показанную на рис. 9.50.

Толщина пластины. Во многих случаях пластины, используемые как конструктивные элементы, имеют постоянную толщину. Если же толщина пластины изменяется, то толщина есть функция двух пространственных координат h=h(x,y), при этом для сохранения плоско-напряженного состояния изменение толщины должно быть достаточно медленным.

Материал пластины. Свойства материала задаются с помощью определяющих соотношений. В данной лекции мы рассмотрим случай линейно упругого, но не обязательно изотропного материала.

Силы, действующие в области . «Областные» силы действуют на внутренние точки области . В общем случае они могут быть двух типов. Во-первых, стандартные объемные силы, определенные как силы, действующие на единицу объема пластины, например, вес тела. Во-вторых, специфические областные силы, действующие по касательной к верхней и нижней поверхностям пластины, например, силы трения, которые могут возникать при относительном движении пластины по другому телу. Эти силы определенным образом должны быть приведены к срединной плоскости пластины.

Заданные поверхностные силы. Поверхностные силы – это известные силы, действующие на точки границы Г. Часто они называются поверхностными усилиями. При решении технических задач необходимо обращать внимание на размерность этих сил, т.к. они могут быть заданы как сила на единицу поверхности или как сила на единицу длины.

Кинематические граничные условия. Кинематические граничные условия задают способы закрепления пластины. Точки на границе области могут быть зафиксированы в одном или в двух направлениях. Дополнительно могут быть заданы условия симметрии или антисимметрии. Если кинематические граничные условия не заданы, то такие граничные условия называются свободными.

9.7.4. Искомые функции

В задачах механики основными неизвестными величинами являются поля перемещений, деформаций и напряжений. Согласно ранее сделанным предположениям, все основные искомые физические переменные не зависят от нормальной координаты z и являются функциями только координат x и y.

Перемещения. Вектор перемещений состоит из двух компонент:

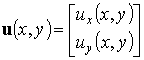. (9.14)

Нормальная компонента перемещений u_z(x,y,z) в общем случае отлична от нуля из-за эффекта коэффициента Пуассона и зависит от z. Однако это перемещение не входит в разрешающее уравнение задачи и может быть вычислено отдельно по найденным основным компонентам.

Деформации. Деформации, лежащие в плоскости, формируют тензор, определяемый тремя независимыми компонентами: , и . Для удобства формулировки конечно-элементных уравнений матричной формы компоненты тензора деформации представим в виде трехкомпонентного «вектора деформации»:

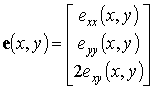. (9.15)

Удвоенная компонента представляет собой деформацию сдвига и используется для сокращения записи выражения энергии деформации. Остальные сдвиговые компоненты и равны нулю согласно исходным предположениям. Нормальная компонента обычно не равна нулю из-за эффекта Пуассона. Однако также как перемещение нормальная компонента деформации не входит в разрешающее уравнение как неизвестная. В выражении энергии деформации произведение обращается в ноль, поскольку нормальное напряжение равно нулю по исходным предположениям.

Напряжения. Тензор напряжений также определяется тремя независимыми компонентами , и , лежащими в плоскости пластины. Как и в случае с деформациями для удобства представления конечно-элементных уравнений в матричном виде сформируем трехкомпонентный «вектор напряжений»:

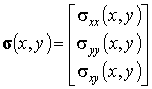. (9.16)

Оставшиеся три компонента тензора напряжений , и равны нулю согласно определению плосконапряженного состояния.

Объемные внутренние силы могут быть получены путем интегрирования напряжений по толщине пластины. В случае однородного распределения напряжений по координате z, данные силы, также образующие тензор, легко могут быть вычислены согласно следующей формуле:

, , . (9.17)

В литературе такие силы часто называются мембранными силами (рис. 9.51).

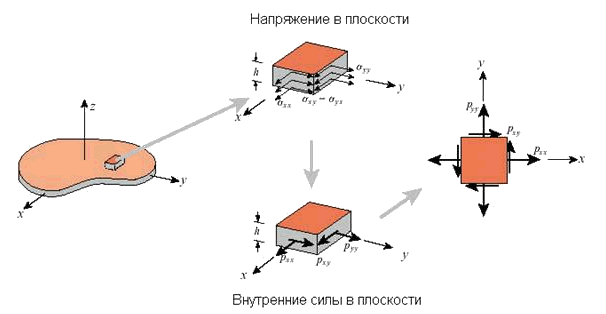
Рис. 9.51. Внутренние силы и напряжения, действующие на произвольный элемент мембраны.

9.7.5. Разрешающие уравнения

Система разрешающих уравнений классической линейной теории упругости схематично представлена на рис. 9.52 в виде так называемой диаграммы Тонти.

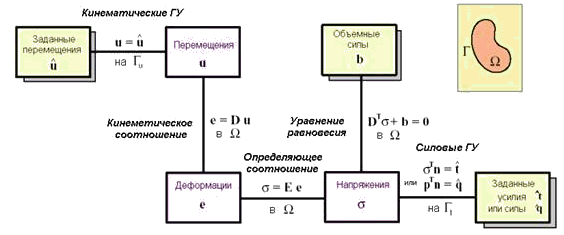
Рис. 9.52. Система разрешающих уравнений классической линейной теории упругости в виде диаграммы Тонти.

Система разрешающих уравнений теории упругости относительно трех неизвестных физических полей перемещений, деформации и напряжений состоит из трех групп уравнений: кинематических соотношений, определяющих уравнений и уравнений равновесия в области тела. При отсутствии начальных напряжений в теле эта система уравнений может быть записана в следующем символьно-матричном виде:

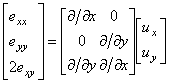, (9.18а)

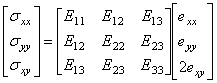(9.18б)

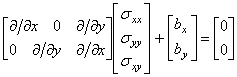(9.18в)

Кроме уже введенных матричных векторов перемещений, деформаций и напряжений, записанная система трех матричных уравнений содержит вектор объемных сил с компонентами b_x, b_y, входящий в уравнение равновесия, матрицу упругих модулей с компонентами E_ij, связывающую напряжения и деформации в точке тела, а также две символические матрицы, состоящие из частных производных по пространственным координатам. Заметим, что символические матрицы, входящие в кинематическое соотношение и в уравнение равновесия, совпадают с точностью до операции транспонирования.

В матричном виде система (4.5) может быть представлена в следующем виде:

(9.19)

где E – симметричная матрица упругих модулей, D – символическая матрица, состоящая из частных производных, b – матричный вектор объемных сил.

Заметим, что приведенная система уравнений (9.19) несколько отличается от координатной или тензорной форм записи полной системы уравнений теории упругости, часто используемым в литературе. Достоинство данной формулировки состоит в том, что все уравнения уже записаны в матричном виде, наиболее удобном для вывода соотношений метода конечных элементов.

Если материал пластины является изотропным, то как известно из теории упругости компоненты матрицы упругих модулей E могут быть выражены через технические константы материала: модуль упругости E, коэффициент Пуассона и модуль сдвига G:

,

,

,

.

При этом напомним, что только две из перечисленных технических констант являются независимыми. Формула, связывающая модуль упругости E, коэффициент Пуассона и модуль сдвига G, имеет следующий вид:

.

9.7.6. Граничные условия

В классической задаче теории упругости граничные условия, заданные на поверхности Г, могут быть двух типов: кинематические граничные условия и силовые граничные условия. Предполагается, что каждый тип граничных условий задан на своей части поверхности: Г_u и Г_t соответственно (Рис. 9.53).

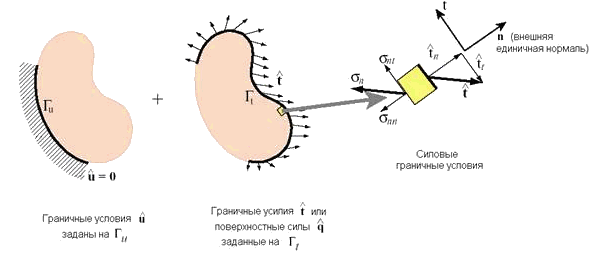
Рис. 9.53. Кинематические и силовые граничные условия в плоской задаче теории упругости.

Кинематические граничные условия заданы на части поверхности Г_u и могут быть записаны в следующей формуле:

(9.20)

Правая часть соотношения (9.20) представляет собой заданные перемещения точек поверхности. Во многих случаях эти перемещения равны нулю. Например, в случае, если часть поверхности каким-либо образом закреплена, как показано на рис. 9.53.

Силовые граничные условия заданы на части поверхности Г_t и могут быть записаны в следующей форме:

(9.21)

В формуле (9.21) правая часть представляет собой заданные поверхностные силы или поверхностные усилия, а левая часть – вектор напряжений на площадке с нормалью n.

Альтернативная форма записи силовых граничных условий может быть записана в виде:

(9.22)

где и .

Вектор напряжений на площадке с нормалью n определяется согласно формуле Коши через компоненты внешней нормали к поверхности и компоненты тензора упругости в точке поверхности:

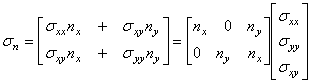, (9.23)

где n_x и n_y обозначают декартовы координаты единичной нормали к поверхности n^(e) (направляющие косинусы). Таким образом (9.21) может быть записано в виде двух скалярных соотношений и .

В некоторых случаях бывает удобно записать условие (9.21) в локальной системе координат, образованной нормалью n<B< i>> и ортом касательной t:

, (9.24)

где соответствующие компоненты напряжений в локальной системе координат могут быть выражены следующим образом:

,

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00