Главная
9.7.8.
Конечно-элементная формулировка плоской задачи теории упругости: вывод СЛАУ МКЭ
9.7.8.1.
Принцип минимума потенциальной энергии
Согласно вариационному принципу Лагранжа полная потенциальная энергия тела, находящегося в равновесии под действием внешних объемных и поверхностных сил, достигает минимума на истинном поле перемещений, т.е. на поле перемещений, удовлетворяющем полной системе уравнений теории упругости. Отсюда следует, что вариация функционала энергии на истинных перемещениях должна быть равна нулю:
.
(9.36)
Поскольку полная потенциальная энергия тела складывается из потенциальной энергии деформации тела и работы внешних сил (5.1), то последнее соотношение (9.36) может быть записано следующим образом:
(9.37)
где 
- вариация
потенциальной энергии деформации тела, 
- вариация работы
внешних сил, совпадающая по своему виду с элементарной работой внешних сил на
возможных перемещениях.
Вычислим первое слагаемое в формуле (9.37).
В предыдущей лекции было отмечено, что потенциальная энергия деформации тела
представляет собой интеграл по объему тела от удельной потенциальной энергии:
(9.38)
где W – удельная потенциальная энергия тела, или так называемый упругий потенциал.
Выражение упругого потенциала было получено в предыдущей лекции и в матричном виде может быть записано следующим образом:
(9.39)
Как следует из соотношения (9.39) упругий потенциал представляет собой квадратичную форму относительно компонент вектора деформации. Запишем соотношение (9.39) в развернутом виде:
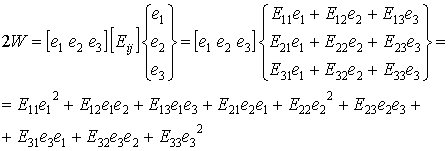(9.40)
В данной формуле для сокращений записей были
использованы индексные обозначения компонент вектора деформации:
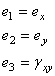(9.41)
С учетом симметрии матрицы упругих модулей:
, 
(9.42)
соотношение (6.5) может быть записано в виде квадратичной формы:
. (9.43)
Применим теперь операцию варьирования к
выражению потенциальной энергии деформации тела:
.
(9.44)
Отметим, что в данном случае потенциальная
энергия является функцией деформаций, которые в свою очередь зависят от поля
перемещений. Поэтому необходимо использовать правило варьирования сложной
функции многих переменных:
,
(9.45)
где перемещения являются независимыми варьируемыми функциями, а деформации – варьируемыми функциями, зависящими от перемещений.
Заметим также, что с формальной точки зрения математически операция вычисления вариации функции эквивалентна операции вычисления дифференциала функции, т.е. выполняется по тем же правилам:
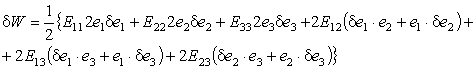(9.46)
Перегруппировав слагаемые в соотношении
(9.46), получим выражение 
в виде:
.
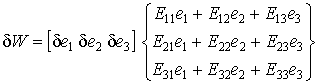(9.47)
Окончательно вариация упругого потенциала может быть записана в следующем матричном виде:
,
(9.48)
где
- вариация
вектора деформаций.
Тогда вариация потенциальной энергии деформации тела будет записана следующим образом:
.
(9.49)
Вариация работы внешних сил находится простым варьированием соотношения (9.27) с учетом того, что варьируемой независимой функцией является поле перемещений:
, (9.50)
где 
- вариация
вектора перемещений.
Заметим еще раз, что выражение (9.50)
совпадает с выражением элементарной работы внешних сил на возможных
перемещениях
.
9.7.8.2.
Вывод разрешающих уравнений
Согласно рассмотренному выше алгоритму конечно-элементной дискретизации область тела представляется в виде множества не пересекающихся подобластей. В соответствии с этим разбиением объемные и поверхностные интегралы, входящие в выражения потенциальной энергии и работы внешних сил, равны сумме интегралов по конечным элементам. Следовательно, интегральные соотношения (9.49) и (9.50) будут представлены в виде:
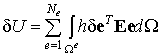(9.51)
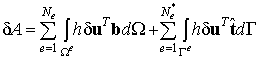(9.52)
где 
- общее число конечных элементов, 
- число конечных
элементов, выходящих на границу области.
Для повышения универсальности
рассматриваемого алгоритма введем в рассмотрение так называемые матрицы
кинематических связей ае, состоящие из нулей и единиц. Введем также
глобальный вектор узловых перемещений U, состоящий из
декартовых координат векторов перемещений в узлах конечно-элементной сетки. При
этом нумерация узлов сетки называется глобальной нумерацией, в отличие
от локальной нумерации узлов на элементе. Размер глобального вектора узловых
перемещений равен 
, где 
- общее число узлов
конечно-элементной сетки. Очевидно, что компоненты любого элементного вектора
перемещений содержатся в соответствующих позициях глобального вектора
перемещений. Матрицы кинематических связей как раз и устанавливают взаимосвязь
между этими векторами на основе того очевидного факта, что любой узел любого
элемента имеет свой локальный номер в пределах данного элемента и уникальный
глобальный номер в пределах всей конечно-элементной сетки. Таким образом, связь
между векторами может быть выражена следующим соотношением:
. (9.53)
Когда формулы (5.6б) и (5.7б), представляющие собой перемещения и деформации в любой точке конечного элемента, могут быть представлены следующим образом:
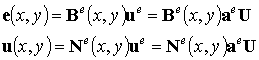(9.54)
Соответственно вариации функций U и e вычисляются следующим образом:
,
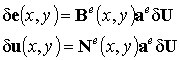(9.55)
поскольку именно глобальный вектор перемещений содержит независимые варьируемые функции – перемещения в узлах конечно-элементной модели. Обратим внимание, что несмотря на зависимость матрицы интерполирующих функций Ne и матрицы градиентов Be от пространственных координат x и y, эти матрицы не являются варьируемыми функциями.
Применим операцию транспонирования к выражению (9.55). Согласно правилам вычисления транспонированной матрицы, представляющей собой произведение трех матриц, запишем:
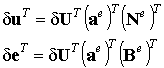(9.56)
Подставим теперь выражения (9.56) и (9.54) в формулу вариации потенциальной энергии (9.51). Получим:
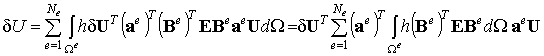, (9.57)
где вектора U и 
вынесены за знаки
суммы и интеграла, поскольку эти вектора состоят из независимых скалярных
величин, матрицы ае, состоящей из нулей и единиц, вынесены только за
знак интеграла, так как зависят от номера конечного элемента е.
Введем следующие обозначения:
,
(9.58)
,
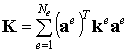(9.59)
где ke называется элементной матрицей жесткости, K называется глобальной матрицей жесткости. В результате получим компактное матричное выражение потенциальной энергии тела:
.
(9.60)
Аналогично предыдущему запишем выражение элементарной работы внешних объемных и поверхностных сил:
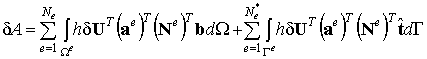. (9.61)
Введем стандартные обозначения элементных векторов сил:
,
(9.62)
, (9.63)
где 
называется элементным вектором узловых сил,
статически эквивалентным заданным объемным силам, 
называется
элементным вектором узловых сил, статически эквивалентным заданным
поверхностным силам.
Аналогично предыдущему элементные вектора сил объединяются в глобальные вектора:
,
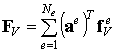(9.64)
,
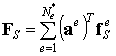(9.65)
где FV называется глобальным вектором узловых сил, статически эквивалентным заданным объемным силам, FS называется глобальным вектором узловых сил, статически эквивалентным заданным поверхностным силам.
Отметим, что процесс формирования глобальной матрицы жесткости и глобальных векторов узловых сил в методе конечных элементов называется ансамблированием.
Таким образом, формула (9.61) будет представлена в следующем компактном виде:
(9.66)
Подставим полученные выражения (9.60) и (9.66) в основную формулу принципа минимума потенциальной энергии Лагранжа (9.37):
(9.66)
Отсюда получаем:
.
(9.67)
Поскольку вариация глобального вектора узловых перемещений представляет собой вектор, состоящий из независимых произвольных вариаций узловых перемещений, то в общем случае он отличен от нуля. Следовательно, в ноль должно обращаться выражение в круглых скобках. Откуда получаем разрешающую систему конечно-элементных уравнений относительно глобального вектора узловых перемещений:
(9.68)
Матричное уравнение (9.68) представляет собой стандартную форму записи системы линейных алгебраических уравнений метода конечных элементов (СЛАУ МКЭ). Особенности формирования входящих в нее матриц и векторов и особенности решения СЛАУ будут рассмотрены в следующих разделах.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
