Главная
9.8.
Треугольный линейный конечный элемент: система координат и интерполяция.
9.8.1.
Введение
В данной лекции будут рассмотрены особенности формирования системы линейных алгебраических уравнений метода конечных элементов (СЛАУ МКЭ) на примере трехузлового треугольного элемента с линейной интерполяцией перемещений, применяемого для решения плоской задачи теории упругости. Для краткости будем называть такой элемент линейным треугольным конечным элементом.
Этот элемент имеет ряд отличительных особенностей:
Он принадлежит к семейству так называемых изопараметрических элементов, о чем будет говориться в следующих лекциях;
Он позволяет получить выражения элементных матриц жесткости и элементных векторов сил в замкнутой форме, что означает отсутствие необходимости в численном интегрировании при вычислении элементных матриц жесткости и элементных векторов сил;
Точность решения, обеспечиваемая данным элементом, не может быть повышена путем добавления внутренних степеней свободы.
В дополнение хотелось бы отметить, что линейный треугольный конечный элемент имеет определенное историческое значение. Он был одним из двух первых конечных элементов, представленных в статье Мартина, Тернера, Клоха и Топпа в 1956 году. Эта публикация общепризнанно считается началом современного метода конечных элементов.
Хотя линейный треугольный конечный элемент в настоящее время реже используется при расчетах конструкции ввиду его низкой точности, тем не менее, он широко используется в тех случаях, когда нет необходимости в высокоточных расчетах, например, концентрации напряжений в конструкции. Другая причина широкого применения треугольного элемента состоит в том, что он очень удобен при использовании в алгоритмах автоматической генерации сетки, например, в широко известном и популярном алгоритме триангулизации по Делоне.
9.8.2.
Параметрическое представление функций
В дальнейшем изложении существенным образом будет использоваться понятие параметрического представления функции. Совместно с алгоритмами численного интегрирования данный подход играет ключевую роль в системной разработке различных типов конечных элементов для решения двумерных и трехмерных задач механики деформируемых тел.
Основная идея параметрического представления
функции может быть продемонстрирована на простейшем примере. Рассмотрим
каноническое уравнение окружности единичного радиуса с центром в начале
координат:
(9.69)
Кроме канонического представления (7.1)
уравнение окружности может быть представлено в виде стандартной функциональной
зависимости:
,
(9.70)
а также в полярной системе координат:
(9.71)
В представлении (9.71) 
есть полярный угол,
который может быть интерпретирован в виде независимого скалярного параметра,
меняющегося в заданных пределах. Очевидно, что подстановка (9.71) в (9.69) дает
тождественное равенство.
В общем случае параметрическое представление
кривой линии на плоскости или в пространстве имеет вид:
,
(9.72а)
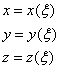, (9.72б)
где 
- независимый
скалярный параметр, меняющейся в заданных пределах.
Вид функций, входящих в (9.72), может быть
любым. Главное условие, наложенное на эти функции, состоит в том, чтобы каждому
значению параметра однозначно
соответствовала бы точка на плоскости, имеющая координаты 
, или
в пространстве - 
.
Аналогично определяется параметрическое
представление куска плоскости на координатной плоскости или куска поверхности в
трехмерном пространстве:
,
(9.73а)
,
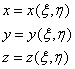(9.73б)
Здесь 
- система двух независимых
параметров, меняющихся в заданных пределах. Вид функций, входящих в (9.73),
может быть также любым. Главное условие, наложенное на эти функции, состоит в
том, чтобы имело место взаимооднозначное соответствие
системы параметров и координат 
в соотношении (7.5а).
В случае соотношения (9.73б) достаточно выполнения одного соответствия точки на
плоскости 
и точки на поверхности
в пространстве 
.
Параметрическое представление функций существенным образом используется в алгоритмах метода конечных элементов.
9.8.3.
Система координат треугольного элемента
Геометрия трехузлового
треугольного конечного элемента задается тремя угловыми точками в плоскости - узлами конечного элемента (Рис. 9.57). Локальные номера
узлов на элементе: 1, 2, 3; причем узлы нумеруются таким образом, чтобы обход
по контуру элемента был бы против часовой стрелки, если смотреть со стороны
внешней нормали к плоскости пластины. Напомним, что внешняя нормаль к плоскости
пластины совпадает с положительным направлением глобальной оси z. Положение узлов определяется
декартовыми координатами в глобальной системы координат:
(9.74а)
Линейный треугольный конечный элемент имеет
шесть степеней свободы, образуемые компонентами элементного вектора узловых
перемещений:
(9.74б)
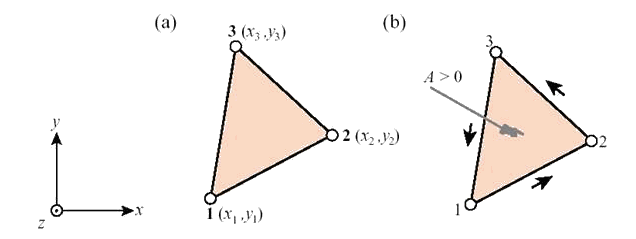
Рис. 9.57. Линейный треугольный конечный элемент: (а) – геометрия элемента; (б) – положительное направление обхода контура элемента.
Обозначим площадь элемента через А.
Согласно известной формуле линейной алгебры, площадь плоского треугольника
может быть вычислена с помощью определителя, составленного из координат вершин
треугольника. Следовательно, площадь линейного треугольного конечного элемента
равна:
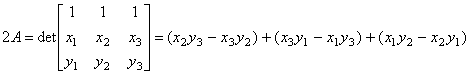(9.75)
Заметим, что площадь области, определяемой формулой (9.75), имеет знак. Она положительна, если локальная нумерация узлов (1, 2, 3) выполнена против часовой стрелки, если смотреть со стороны внешней нормали к плоскости пластины, как это было отмечено выше и показано на рисунке 9.57. В противном случае, знак А будет отрицательным, что сигнализирует об ошибке. Такое соглашение будет использоваться и в дальнейшем изложении материала.
Кроме глобальной системы координат 
введем локальную
параметрическую систему координат в плоскости элемента, задаваемую тремя
переменными величинами:
(9.76)
Эти три локальные параметрические координаты
в литературе по МКЭ называются также естественными и треугольными.
С помощью введенной системы координат устанавливается взаимооднозначное
соответствие между глобальными декартовыми координатами произвольной точки
элемента и тремя скалярными параметрами :
, (9.77)
Сразу обратим внимание на кажущееся
противоречие между формулами (9.77) и (9.73а), которое легко устраняется, если
допустить наличие связи между параметрами . На самом деле, так оно и есть: три треугольные координаты
не являются независимыми, а связаны одним соотношением:
(9.78)
Очевидно, что из соотношения (9.78) можно
выразить, например, координату 
через другие две 
. Тогда соотношение (9.77) примет стандартный вид (9.73а).
Однако, использование трех параметров оказывается
более удобным с точки зрения вычислений и разработки эффективных численных
алгоритмов, о чем всегда необходимо помнить, когда имеешь дело с вычислительной
механикой.
На рисунке 9.58 дано геометрическое пояснение математического смысла введенных координат.
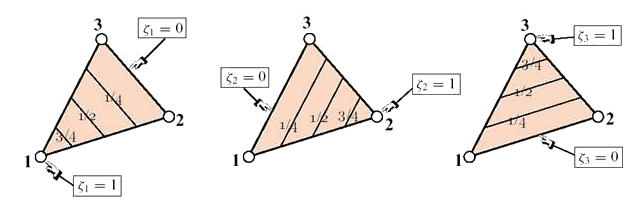
Рис. 9.58. Треугольные координаты.
Три уравнения, записанные в виде:
(9.79)
геометрически представляют собой множество прямых линий, параллельных стороне, противоположной i-му узлу.
Например, уравнения сторон треугольного
элемента 1-2, 2-3 и 3-1 будут иметь следующий вид:
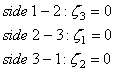(9.80а)
Три вершины треугольного элемента будут
иметь следующие локальные координаты:
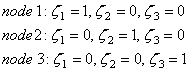(9.80б)
В качестве примера приведем также координаты
средних точек сторон треугольного элемента и геометрического центра элемента:
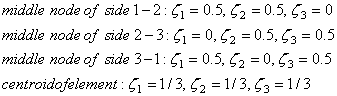(9.80в)
Еще раз напомним, что три параметра не
являются независимыми и связаны одним дополнительным соотношением:
9.8.4.
Интерполяционные соотношения линейного треугольного элемента
Рассмотрим произвольную непрерывную функцию
двух переменных, которая изменяется линейно в пределах некоторой плоской
треугольной области. В декартовой системе координат эта функция может быть
записана следующим образом:
,
(9.81)
Где 
- произвольные
постоянные коэффициенты.
Пусть теперь мы хотим ввести аппроксимацию данной
функции в пределах треугольного элемента. Обозначим через:
,
(9.82)
значения данной функции в соответствующих узлах конечного элемента – так называемые узловые значения функции.
С помощью этих значений могут быть
определены неизвестные коэффициенты в представлении (9.81). В самом деле,
получим:
,
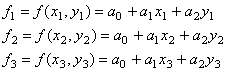(9.83)
Соотношения (9.83) представляют систему трех
линейных алгебраических уравнений относительно неизвестных коэффициентов . Решив систему (9.83), получим однозначное выражение функции
(9.81) через ее узловые значения. Однако, это выражение достаточно сложное и
неудобное в использовании. Поэтому используют представление функции не в
глобальной, а в локальной системе координат на элементе. Очевидно, что если
установлено взаимооднозначное соответствие между
глобальной и локальной системами координат, то и выражения функции в различных
координатах будут соответственными друг другу.
Используя данный подход, представим функцию
(9.81) в треугольных координатах через ее узловые значения следующим образом:
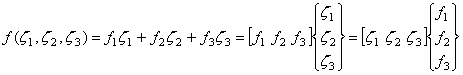(9.84)
Соотношение (9.84) называется линейным интерполирующим соотношением произвольной непрерывной функции f в треугольных координатах.
В следующей лекции, пользуясь введенными понятиями, получим расчетные соотношения линейного треугольного конечного элемента.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
