Главная
9.9.
Треугольный линейный конечный элемент: вывод расчетных соотношений
9.9.1.
Преобразование координат
Математические величины,
которые тесно связаны с геометрией треугольного конечного элемента, естественным
образом выражаются через треугольные координаты 
. С другой стороны, такие физические величины как
перемещения, деформации и напряжения часто выражены в декартовых координатах 
. Следовательно, необходимы уравнения, связывающие эти две
системы координат, с помощью которых возможно переходить от одной системы
координат к другой.
Используя универсальное соотношение (9.84),
глобальные декартовые координаты произвольной точки на треугольном элементе могут быть выражены
через глобальные координаты узлов элемента и локальные треугольные координаты
этой же точки 
:
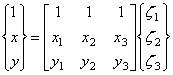, (9.85)
где 
- глобальные декартовы координаты узлов треугольного
элемента.
Поясним матричное выражение (9.85). Мысленно развернем его. Тогда первое уравнение будет выражать собой тот факт, что сумма трех локальных координат равна единице. Два последних уравнения представят собой развернутые интерполяционные соотношения глобальных координат точек треугольного элемента (См. ур-е 9.84):
(9.86)
Разрешим систему (9.85) относительно вектора
. Найдем обратную матрицу к матрице системы (9.85) и запишем
решение в виде:
,
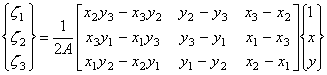(9.87)
где А – определитель матрицы системы (9.85), численного совпадающий с площадью треугольного элемента (9.75).
Введем обозначения:
,
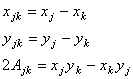(9.88)
где 
- математически
представляет собой площадь треугольника, образованного двумя вершинами элемента
и центром глобальной системы координат; 
- проекции длин сторон
элемента на оси глобальной системы координат. Очевидно, что если начало
координат расположено в центре элемента, то 
.
В обозначениях (9.88) решение (9.87) примет вид:
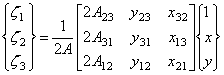(9.89)
9.9.2.
Вычисление частных производных
Из соотношений (9.86) и (9.89) легко вычисляются частные производные по соответствующим координатам:
, 
, 
, 
, 
(9.90)
Во второй строке формул (9.90)
последовательность представляет собой круговую
перестановку индексов. Например, если 
, то 
и 
. Если 
, то 
и 
.
Рассмотрим произвольную непрерывную функцию
двух переменных, которая изменяется линейно в пределах некоторой плоской
треугольной области (См. формулы 9.81 и 9.84). Эта функция может быть
представлена как в глобальной декартовой системе координат , так и в локальной треугольной системе координат . Представим ее как сложную функцию многих переменных:
(9.91)
Вычислим теперь частные производные функции (9.91) по глобальным координатам, воспользовавшись правилом дифференцирования сложной функции многих переменных:
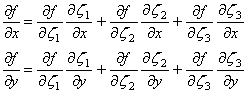(9.92)
Подставим (9.90) в (9.92). Получим выражения частных производных произвольной непрерывной функции по глобальным координатам через три частные производные той же функции по локальным треугольным координатам:
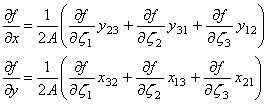(9.93)
Окончательно в матричной форме система частных производных произвольной непрерывной функции по глобальным координатам примет вид:
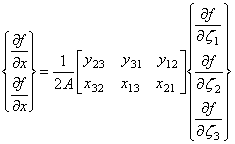(9.94)
Таким образом, мы получили все необходимые математические формулы для вывода уравнений, описывающих треугольный линейный конечный элемент.
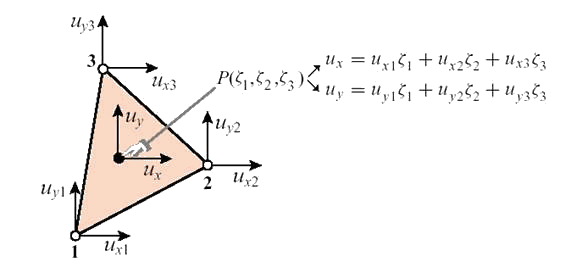
Рис. 9.59. Интерполяция перемещений в пределах треугольного линейного конечного элемента.
9.9.3.
Вывод уравнений треугольного линейного конечного элемента
9.9.3.1.
Интерполяция перемещений
В случае треугольного линейного конечного
элемента предполагается, что перемещения в пределах элемента изменяются линейно
по пространственным координатам. Это означает, что компоненты вектора
перемещений в любой произвольной точке элемента 
могут быть
представлены с помощью интерполяционного соотношения 9.84, которое в данном
случае примет вид:
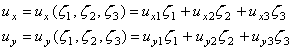(9.95)
Здесь 
- компоненты вектора
перемещений в узлах конечного элемента (Рис. 8.1).
Интерполяционное соотношение для перемещений (8.11) может быть также представлено в стандартной для метода конечных элементов матричной форме (см. формулы 9.30):
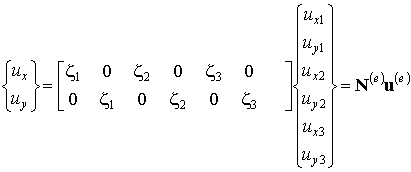, (9.95а)
где 
- матрица
интерполирующих функций, 
- элементный
вектор узловых перемещений.
Очевидно, что в рассматриваемом случае
треугольного линейного конечного элемента интерполирующие функции 
равны треугольным
координатам:
(9.96)
9.9.3.2.
Кинематические уравнения
Компоненты тензора деформаций (вектор деформаций) вычисляются путем дифференцирования вектора перемещений, что приводит к общей формуле (9.31б):
(9.97)
где 
- матрица градиентов.
Вычислим матрицу градиентов. Согласно формуле (9.32):
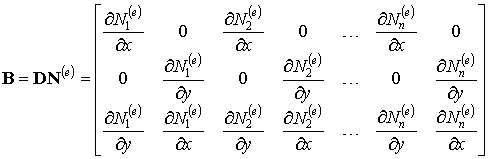(9.98)
Интерполирующие функции могут быть интерпретированы как сложные функции многих переменных:
(9.99)
С другой стороны, в явном виде они совпадают с треугольными координатами элемента (см. формулу 9.96). Тогда применяя формулы вычисления частных производных функций подобного типа по глобальным координатам (9.93) и (9.90), получим выражение матрицы градиентов:
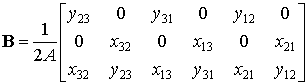(9.100)
Обратим внимание, что деформации (9.97) получились постоянными на элементе, поскольку компоненты матрицы градиентов – проекции сторон элемента – постоянные величины.
9.9.3.3.
Определяющие соотношения
Определяющее соотношение анизотропного идеально-упругого материала записывается в виде хорошо известного закона Гука. В матричном виде оно было получено в лекции 9.7.7. Здесь мы его еще раз приведем для полноты изложения:
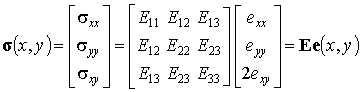, (9.101)
где 
- упругие модули
материала.
Если считать, что упругие свойства материал не меняются на элементе, то, поскольку деформации постоянны, напряжения также постоянны на элементе.
9.9.3.4.
Элементные матрицы жесткости
Для задачи о плоско-деформированном состоянии тела общий вид матриц жесткости был получен в лекции 6. Напомним его:
(9.102)
Как было отмечено выше, матрицы градиентов и упругих модулей постоянны для рассматриваемого треугольного линейного конечного элемента. Следовательно, их произведение может быть вынесено за знак интеграла:
(9.103)
Если элемент имеет постоянную толщину (h=const), то h также выносится за знак интеграла по площади элемента, который, таким образом, легко вычисляется и будет равен площади элемента А. В результате, получим выражение элементной матрицы жесткости:
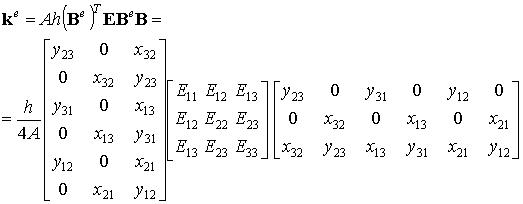(9.104)
Заметим, что все геометрические переменные и модули упругости могут быть разными на разных элементах и, следовательно, зависят от номера элемента е.
9.9.3.5.
Элементные вектора узловых сил
Для простоты рассмотрим сейчас только вычисление элементного вектора узловых сил, статически эквивалентных заданным объемным силам. Причем, пусть объемные силы представляют собой плотность сил собственного веса тела (сила на единицу объема):
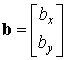(9.105)
Согласно общей формуле вычисления вектора объемных узловых сил:
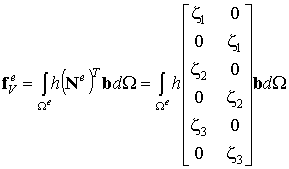(9.106)
Пусть толщина элемента постоянна и плотность
объемных сил также постоянна. Тогда h и b могут быть вынесены за знак интеграл и
необходимо вычислить только интегралы от 
по
площади элемента:
(9.107)
Здесь мы воспользовались известной математической формулой вычисления интеграла по площади треугольника:
(9.108)
Таким образом, вычисляя интегралы от интерполирующих функций и перемножая полученную матрицу на вектор b, получим окончательное выражение элементного вектора узловых сил, статически эквивалентных заданным постоянным объемным силам:
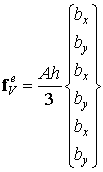(9.109)
Заметим, что полученные компоненты вектора узловых сил совпадают с результатом простого равномерного распределения суммарной силы, равной Ahb, между тремя узлами.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
