Главная
9.11.
Четырехсторонние двумерные элементы
9.11.1. Естественные координаты элемента
Согласно общей концепции построения
произвольного изопараметрического конечного элемента,
введем в рассмотрение естественную локальную систему координат на
элементе, соответствующую геометрии данного типа элемента. Естественной
системой координат трехстороннего элемента являются треугольные координаты 
. Естественной системой координат плоского четырехстороннего
элемента является система координат 
, показанная на рис. 9.64 для двух вариантов
четырехстороннего элемента, имеющего прямолинейные либо криволинейные стороны.
Данная система координат относится к известному широкому классу недекартовых координат – криволинейных косоугольных, в
общем случае, координат. Несмотря на очевидные отличия от декартовой
системы, криволинейные косоугольные координат обладают сходными математическими
свойствами.
Рис. 9.64. Четырехсторонние двумерные элементы в криволинейных косоугольных координатах.
Локальная система координат является
масштабированной. Это означает, что каждая координата изменяется в пределах от
-1 на одной стороне элемента до +1 на противоположной стороне, принимая нулевое
значение на медианах. Заметим, что пределы изменения локальных координат могут
быть выбраны произвольно, например, от 0 до 1. Преимущество введенных пределов
состоит в том, что они обеспечивают эффективное применение формул
интегрирования Гаусса, что будет обсуждаться в следующих лекциях.
При разработке алгоритмов МКЭ часто бывает
удобно визуализировать произвольный конечный элемент в декартовых координатах
на плоскости (Рис. 9.65). Любой
четырехсторонний конечный элемент в этом случае может быть представлен
квадратом со стороной 2 в безразмерных единицах в пределах 
. Взаимооднозначное преобразование
между локальной системой координат и глобальной 
описывается математическими
уравнениями общего вида:
,
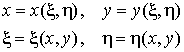(9.124)
В случае произвольного двумерного конечного элемента первая часть формул (9.124) могут быть представлена следующим образом:
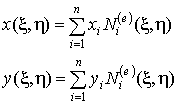, (9.125)
где n – число узлов на элементе.
Соотношения типа (9.124) или (9.125) носят название изопараметрического отображения. Вопрос корректности отображения может быть достаточно острым при расчетах методом конечных элементов. Необходимо правильное построение сетки конечных элементов, чтобы не было нарушения взаимооднозначности отображения (Рис. 9.65).
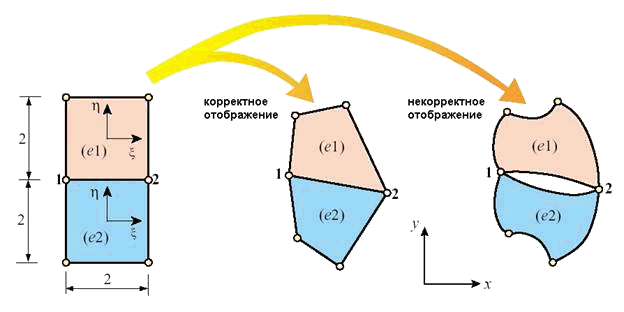
Рис.
9.65. Отображение элемента, заданного в естественных локальных координатах , на тот же элемент
в глобальной системе координат .
В случае корректного отображения имеет место
взаимооднозначное соответствие точек элемента в
плоскостях и . В случае некорректного отображения взаимооднозначное
соответствие нарушается. Так например, видно, что
любой одной точке на линии 1-2 в плоскости соответствует две
точки в плоскости .
9.11.2.
Четырехсторонний билинейный элемент
Четырех-узловой четырехсторонний конечный элемент является простейшим представителем семейства четырехсторонних двумерных элементов. Его вид показан на рис. 9.66, а базовые интерполяционные соотношения представлены следующим образом:
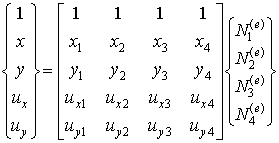(9.126)
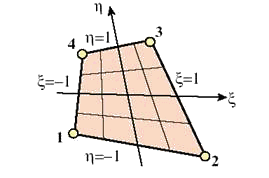
Рис. 9.66. Четырех-узловой четырехсторонний билинейный элемент.
Функции формы элемента выражены следующими соотношениями через локальные естественные координаты:
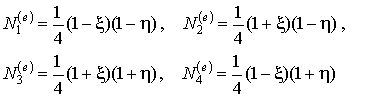(9.127)
Отметим, что функции формы (9.127)
изменяются линейно вдоль координатных линий 
и 
. Однако, они не являются линейными полиномами как в случае
треугольного линейного элемента. Такие функции и соответственно элементы, ими
описываемые, носят название билинейных. На рис.
9.67 приведен графический вид одной из функций формы.
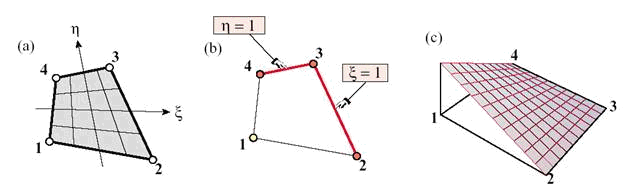
Рис. 9.67. Четырехсторонний билинейный элемент: (а) геометрия элемента; (б) уравнения сторон,
противоположных
первому узлу; (в) вид функции формы 
.
9.11.3.
Четырехсторонние элементы высшего порядка
Рассмотрим следующие два варианты семейства четырехсторонних элементов: девяти-узловой и восьми-узловой изопараметрический конечный элемент, показанные на рис. 9.68. Очевидное внешнее отличие между этими элементами состоит в наличии или отсутствии внутреннего узла в центре элемента.
Интерполирующие соотношения элемента первого типа, носящего название биквадратичный изопараметрический элемент, имеют вид:
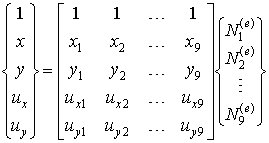(9.128)
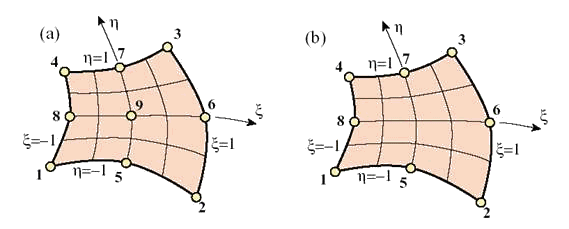
Рис. 9.68. Четырехсторонние конечные элементы высшего порядка: (а) девяти-узловой биквадратичный элемент; (б) восьми-узловой «серендипов» элемент.
Приведем формулы для некоторых характерных функций формы биквадратичного конечного элемента (Рис. 9.69):
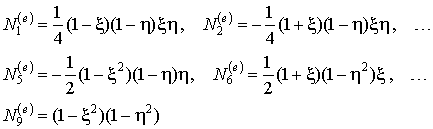(9.129)
Интерполирующие соотношения элемента второго типа, носящего название изопараметрический элемент серендипова семейства, имеют вид:
,
(9.130)
где функции формы могут быть представлены следующим образом:
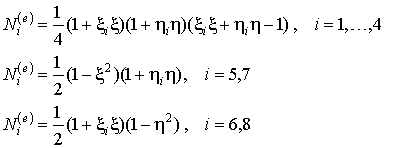, (9.131)
где 
- локальные координаты i-го узла на элементе.
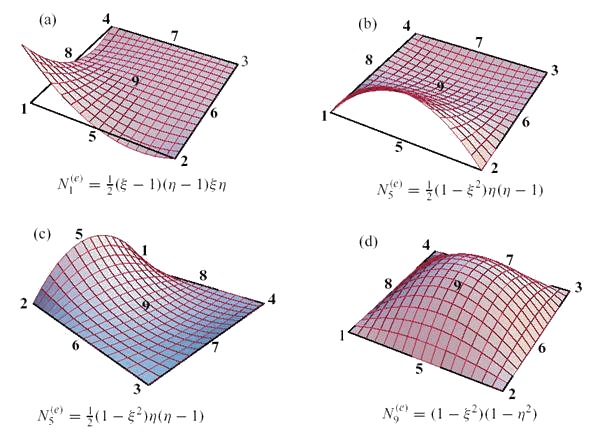
Рис. 9.69. Графики характерных функций формы биквадратичного конечного элемента.
Заметим, что соотношения (9.127) линейного элемента также могут быть представлены в компактной форме, удобной для программирования:
(9.132)
Обратим внимание, что функции формы (9.131)
изменяются по квадратичному закону вдоль координатных линий и . Функция формы, связанная с внутренним девятым узлом
элемента, в англоязычной литературе по МКЭ называется bubble
function, что связано с характерной «пузырчатой» формой
этой функции. В случае элемента серендипова семейства
внутренний узел исключается из рассмотрения путем наложения специальных
кинематических связей:
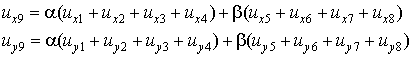(9.133)
Функции формы серендипова
конечного элемента строятся таким образом, чтобы их сумма равнялась нулю, и
порядок аппроксимации был равен двум по обеим локальным координатам. Отсюда
получают два условия для определения констант 
и 
.
9.11.4.
Свойство полноты
Отметим коротко очень важное условие для обеспечения сходимости метода конечных элементов, которому должен подчиняться выбор или построение интерполирующих функций (или, что то же самое, функций формы) – свойство полноты. Множество функций формы называется полным, если эти функции могут точно описать (аппроксимировать) любую линейную функцию перемещений, заданную в виде:
,
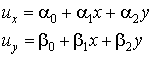(9.134)
где 
- произвольные
константы.
Проверим, удовлетворяют ли рассмотренные функции формы и соответствующие приближенные решения (9.4) данному условию. Вычислим перемещения в узлах согласно соотношениям (9.134):
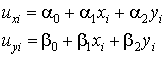(9.135)
Подставим 
в первое
интерполяционное соотношение (9.4). Получим:
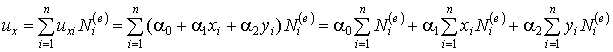
Подставим геометрические интерполяционные
соотношения изопараметрического элемента (9.112) в
последнее выражение. Получим первое из соотношений (9.134). Аналогичные
вычисления могут быть выполнены для компоненты 
. Таким образом, изопараметрические
функции формы удовлетворяют свойству полноты.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
