Главная
9.12.
Вычисление матрицы градиентов изопараметрического
элемента
9.12.1.
Введение
В настоящей и следующей лекции будет подробно рассмотрен алгоритм формирования матриц жесткости конечных элементов (9.58):
(9.136)
В лекции 9.9 мы уже вычисляли матрицу жесткости линейного треугольного элемента. Однако, рассмотренный путь вычислений справедлив только для единственного двумерного элемента - линейного треугольного элемента. Для треугольных элементов высших порядков и для четырехсторонних элементов, широко используемых в конечно-элементных программах, данный подход не применим по причине его неуниверсальности. Дело в том, что линейный треугольный элемент – это единственный двумерный элемент, матрицы жесткости которого могут быть вычислены в явном и замкнутом виде. В остальных случаях, и тем более для трехмерных задач, необходима разработка универсальных алгоритмов, пригодных для программирования.
В общем случае алгоритм формирования ключевой характеристики механического элемента – его матрицы жесткости – включает следующие шаги:
1. Построение функций формы элемента;
2. Вычисление частных производных от функций формы элемента для формирования матрицы градиентов, связывающей деформации и перемещения на элементе;
3. Численное интегрирование по площади (или объему в трехмерном случае) для окончательного вычисления матрицы жесткости.
Ниже будут рассмотрены основные шаги представленного алгоритма на примере изопараметрического четырехстороннего конечного элемента как наиболее характерного представителя семейства универсальных двумерных элементов. При этом будем полагать, что функции формы элемента уже построены (см. лекцию 9.11). Таким образом, основное внимание будет сосредоточено на вычислении частных производных от функций формы и численном интегрировании, а также некоторых других важных моментах эффективного вычисления компонент матриц жесткости.
9.12.2.
Матрица градиентов
Знание выражений частных производных от функций
формы элемента по глобальным координатам 
необходимо для
вычисления матрицы градиентов В, входящей в выражения деформаций (9.31б) и
напряжений (9.35) в произвольной точке элемента. Однако, как было показано в
предыдущих лекциях, функции формы явно зависят только от локальных координат 
, связанных с элементом. Зависимость же от глобальных
координат задается сложной функцией многих переменных.
Итак, рассмотрим произвольный четырехсторонний изопараметрический конечный элемент, заданный n узлами. Матрица градиентов имеет вид (9.32):
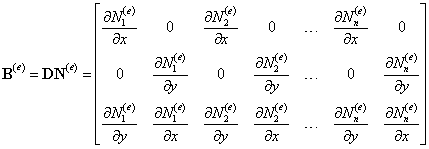(9.137)
Введем следующие обозначения для сокращения записи. Пусть матрица градиентов представлена в виде матричной строки, образованной блоками (3x2):
,
(9.138)
где произвольный блок, связанный с узлом i имеет вид:
,
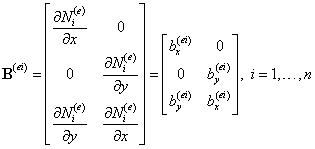(9.139)
Таким образом, необходимо вычислить 2n
компонент матрицы градиентов 
, 
. Дело облегчается тем, что расчетные формулы можно получить
в достаточно общем виде. Покажем это.
9.12.3.
Матрицы Якоби
Пусть функции формы представлены сложной функцией многих переменных:
(9.140)
Пользуясь правилом вычисления частных производных сложной функции, можем записать:
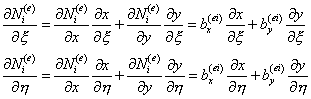(9.141)
Соотношения (9.141) представляют собой
систему двух уравнений относительно неизвестных частных производных , , поскольку производные функций формы по локальным координатам
, 
могут быть легко
вычислены, т.к. функции формы заданы в локальных координатах. Запишем для
удобства (9.141) в матричных обозначения:
,
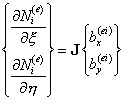(9.142)
где J – матрица
Якоби (называемая также якобианом преобразования), состоящая из
частных производных и определяющая однозначное отображение элемента, заданного
в глобальных координатах 
, на «единичный» элемент в локальной плоскости 
:
Рассмотрим вычисление матрицы Якоби:
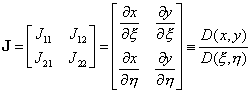(9.143)
Элементы матрицы представляют собой частные производные от глобальных координат точек элемента по соответствующим локальным координатам. Эти производные могут быть легко вычислены для изопараметрического элемента по геометрическим интерполирующим соотношениям (9.125):
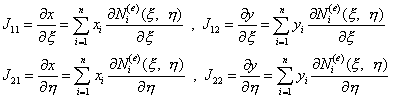(9.144)
После того как определены компоненты матрицы
Якоби, система (9.142) может быть разрешена относительно неизвестных функций , :
,
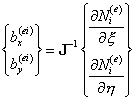(9.145)
где J-1 представляет собой обратную матрицу Якоби.
Согласно правилам вычисления обратных матриц можно записать следующее выражение для J-1:
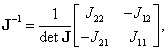(9.146)
где det J - определитель матрицы Якоби, также иногда называемый якобианом:
(9.147)
Окончательно, можно записать выражения 2n искомых компонент матрицы градиентов в развернутом виде:
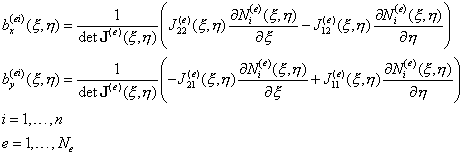, (9.148)
где 
- общее количество
элементов в конечно-элементной сетке, называемое глобальным числом конечных
элементов.
Обратим внимание на особенности формул (9.148):
В общем случае все входящие в формулы переменные
являются функциями локальных естественных координат элемента , включая компоненты матрицы Якоби и якобиан, что следует из
правил их вычисления (9.144);
Компоненты матрицы Якоби и якобиан зависят
только от номера элемента (геометрии элемента), но не связаны с номером узла на
элементе. В то же время, функции формы естественным образом связаны с номером
узла на элементе, что приводит к однозначной зависимости компонент матрицы
градиентов , от локального номера узла на элементе.
Формулы удобны для программирования и применимы для многих разновидностей конечных элементов, в частности, с некоторой модификацией рассмотренный подход легко распространяется и на более сложные трехмерные конечные элементы.
Таким образом, определены выражения 2n искомых компонент матрицы градиентов и, следовательно, могут быть сформированы матрицы градиентов любого элемента согласно формулам (9.138).
Замечание
Заметим, что обратная матрица Якоби определяет
обратное отображение «единичного» элемента в локальной плоскости на элемент,
определенный в глобальных координатах :
По определению якобиана преобразования, можно записать:
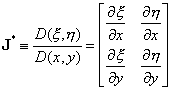, (9.149)
где J* – матрица Якоби обратного преобразования.
Покажем, что J* совпадает с J-1. Для этого достаточно перемножить две матрицы:
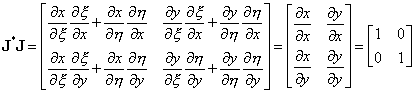, (9.150)
Получение в результате единичной матрицы и доказывает наше предположение о том, что матрица J* совпадает с J-1.
Строгие условия, наложенные на форму элементов, гарантируют взаимооднозначное отображение между элементами в локальной и глобальной плоскостях, что показано ниже.
9.12.4.
Ограничения на геометрию элементов
Для того чтобы имело место взаимооднозначное соответствие между координатами точек элемента в глобальной и локальной системах координат:
и
,
необходимо, чтобы якобиан преобразования (9.147), т.е. определитель матрицы Якоби, был строго положителен.
В литературе, посвященной
математическим аспектам метода конечных элементов доказывается, что это
условие выполняется, если узловые углы, образованные сторонами элемента, лежат
в пределах от нуля до 
(Рис. 9.70).
Рис. 9.70. Четырехсторонний конечный элемент с требуемыми узловыми углами.
Таким образом, необходимо строго следить за
выполнением этого условия и не допускать появления в конечно-элементной сетке
элементов, показанных например на рис. 9.71. В
отмеченных случаях, либо вообще алгоритм формирования , не сможет быть
выполнен из-за деления на ноль, либо решение, несмотря ни на что, будет
получено, но его достоверность не сможет быть обоснована. Заметим, что второй
случай несравненно более опасный, чем первый. Вы сможете
получить ответ и будете думать, что решили задачу. Однако, расчетное решение по построенной модели может оказаться
очень далеким от реальной физической ситуации. Очень опасно, если такое
инженерное решение окажется внедренным и воплощенным в некоторой технической
конструкции или механизме.
Рис. 9.71. Примеры четырехсторонних конечных элементов с некорректными значениями узловых углов.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
