Главная
9.13.
Формирование матрицы жесткости изопараметрического
элемента
9.13.1.
Введение
В настоящей лекции будет подробно рассмотрен алгоритм формирования матрицы жесткости конечных элементов (9.58):
,
(9.151)
где Be - матрица градиентов элемента е;
Ee - матрица упругих модулей элемента е;
- толщина элемента е;
- площадь элемента е.
Вычисление матриц жесткости представляет собой одну из наиболее сложных процедур в алгоритме метода конечных элементов. Проблема формирования включает в себя две задачи:
Структура матрицы. Несмотря на то, что мы уже знаем ее общий вид (9.151), структура матрицы остается пока terra incognita, и кроме того, значительно, хотя и не принципиально, зависит от типа элемента.
Численное интегрирование по области или объему (для трехмерных элементов).
Рассмотрим первую из задач.
9.13.2.
Структура матрицы жесткости
Очевидно, что структура матрицы жесткости
определяется подынтегральным выражением формулы (9.151). Очевидно также, что
толщина элемента не влияет на структуру
матрицы. Поэтому достаточно рассмотреть произведение трех подынтегральных
матриц, чтобы представить себе общий вид матрицы жесткости.
Обозначим:
(9.152)
Тогда:
(9.153)
Раскроем выражение (9.152), перемножив матрицы градиентов и упругих модулей, пользуясь блочным представлением (9.138):
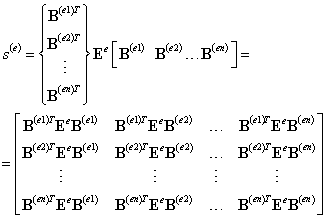, (9.154)
Из выражения (9.154) видно, что искомая матрица имеет блочную структуру, определяемую числом узлов элемента n. При этом каждый блок зависит от номеров двух локальных узлов элемента и может быть записан следующим образом:
,
(9.155)
Соответственно, и матрица жесткости имеет аналогичную матричную структуру, состоящую из блоков:
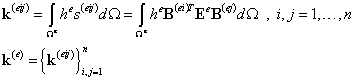(9.156)
В принципе, для разработки алгоритма и программной реализации вычисления матрицы жесткости приведенных формул уже достаточно. Современные языки программирования позволяют производить матричные перемножения с помощью встроенных процедур и функций. Для моделей, содержащих небольшое число элементов, это приемлемо. Однако, число операций, требуемых для перемножения матриц, будет критическим в случае большого количества элементов. Поэтому в коммерческих программах принято проводить эту операцию вручную с тем, чтобы уменьшить конечное число машинных операций перемножения. Кроме того, выполнение этой процедуры вручную полезно с точки зрения понимания полной структуры матрицы жесткости. Поэтому раскроем выражение (9.155), еще раз перемножив матрицы.
9.13.3.
Матрица упругих модулей
Пусть двумерное тело находится в плоско-напряженном или плоско-деформированном состоянии (см. лекцию 9.7). Тогда определяющие соотношения имеют вид:
Плоско-напряженное состояние
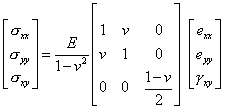(9.157а)
Плоско-деформированное состояние
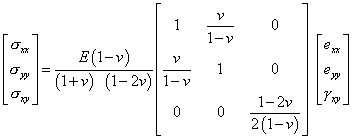(9.157б)
Запишем оба выражения (9.157а и б) в едином виде для повышения универсальности алгоритма:
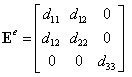, (9.158)
где 
определяются соотношениями (9.157а) и (9.157б).
Заметим также, что выражение (9.158) подходит также для записи матрицы упругих модулей ортотропного материала.
9.13.4.
Выражение компонент матрицы жесткости элемента
Раскроем формулу (9.155), перемножив матрицы:
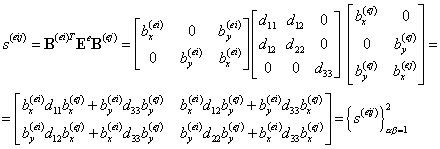(9.159)
Таким образом, видно, что элементарный блок матрицы жесткости двумерного изопараметрического элемента k(eij) (9.156) есть матрица размером 2x2. Поскольку таких блоков в элементной матрице жесткости nxn, то окончательный размер матрицы жесткости есть 2n x2n.
9.13.5.
Численное интегрирование
Полученные выражения (9.159) должны быть проинтегрированы согласно формуле (9.156). Очевидно, что подынтегральные функции могут быть представлены как функции локальных естественных координат элемента согласно формулам (9.112) и (9.138):
(9.160)
Интеграл (9.160) есть интеграл по плоской
замкнутой области. Для его вычисления применим известную математическую
процедуру. Рассмотрим произвольный элемент е одновременно в локальной и
глобальной системах координат. Выделим бесконечно малый элемент площади
конечного элемента 
(Рис.
9.72).
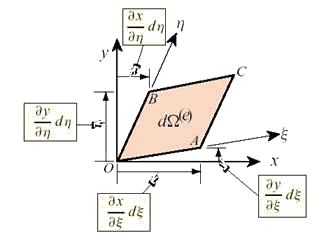
Рис.
9.72. Бесконечно малый элемент площади конечного элемента
в локальной и глобальной системах
координат.
Элемент площади образован сторонами ОА и ОВ
параллелограмма ОАСВ (Рис. 9.72),
которые в свою очередь совпадают с координатными линиями 
и 
(см. рис. 9.72). Пусть
радиус-вектор вершины параллелограмма точки О имеет радиус вектор:
(9.161)
Рассмотрим изменение этого вектора вдоль
координатной линии , определяемую бесконечно малым изменением аргумента 
. Получим радиус-вектор вершины А:
(9.162)
Заметим также, что имеет место очевидное геометрическое соотношение:
(9.163)
Разложим радиус-вектор точки А (9.162) в ряд Тейлора относительно точки О:
(9.164)
Сравнивая соотношения (9.163) и (9.164), найдем с точностью до величин второго и высшего порядка малости вектор, определяющий сторону параллелограмма ОА:
(9.165)
Аналогично рассуждая, найдем вектор, определяющий смежную сторону параллелограмма ОВ:
(9.166)
Вычислим теперь площадь параллелограмма , воспользовавшись тем свойством векторного
произведения, что его модуль равен площади параллелограмма, образованного
векторами, входящими в произведение:
(9.167)
Воспользуемся еще одним свойством векторного произведения, а именно, что оно может быть вычислено с помощью символического определителя:
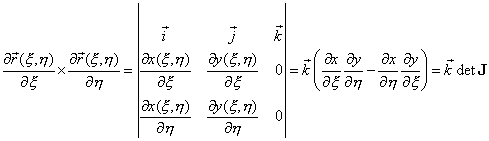, (9.168)
где det J - определитель матрицы Якоби – якобиан, рассмотренный в предыдущей лекции (9.147).
Таким образом, окончательно находим:
(9.169)
С помощью полученного выражения (9.169) можно перейти от интеграла по области к повторному интегралу по локальным координатам в выражении блочных компонент матрицы жесткости (9.160):
(9.170)
Применим известные формулы интегрирования Гаусса для вычисления полученных интегралов. Согласно квадратурам Гаусса, одномерный интеграл от произвольной функции на интервале от -1 до +1 вычисляется следующим образом:
,
(9.171)
где 
- координаты гауссовых
точек (узлов квадратуры);
- весовые коэффициенты
квадратуры;
р – порядок квадратуры.
На рис. 9.73 схематично показаны четыре квадратурные схемы Гаусса соответственно 1-го, 2-го, 3-го и 4-го порядков.
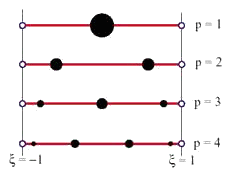
Рис. 9.73. Четыре квадратурные схемы Гаусса порядка р =1, 2, 3, 4. Гауссовы точки показаны черным цветов.
Радиусы точек пропорциональны весовым коэффициентам квадратур.
Формула (9.171) легко распространяется на двумерный интеграл. Ее применение к вычислению интегралов (9.170) дает следующее окончательное алгоритмическое выражение для вычисления компонент матрицы жесткости:
(9.172)
Расположение точек Гаусса на элементе схематично показано на рис. 9.74 для четырех низших квадратур.
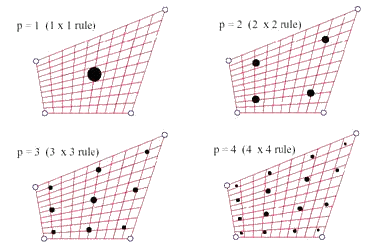
Рис. 9.74. Низшие квадратурные схемы Гаусса порядка р = 1, 2, 3, 4 для четырехстороннего элемента.
Гауссовы точки показаны черным цветов. Радиусы точек пропорциональны весовым коэффициентам квадратур.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
