Главная
9.15.
Формирование и решение глобальной системы конечно-элементных уравнений
9.15.1.
Введение
В предыдущих лекциях были сформированы все необходимые элементные вектора объемных и поверхностных узловых сил, а также элементные матрицы жесткости. Как правило, это является одним из самых сложных этапов при разработке программной реализации метода конечных элементов. Вторым важным этапом будет сборка глобальных матриц жесткости и векторов нагрузки, формирование системы линейных алгебраических уравнений и решение СЛАУ МКЭ.
Матричное уравнение (9.68) представляет собой стандартную форму записи системы линейных алгебраических уравнений метода конечных элементов (СЛАУ МКЭ):
(9.193)
где K – глобальная матрица жесткости конечно-элементной модели;
U – глобальный вектор степеней свободы (узловых перемещений) модели;
FV – глобальный вектор узловых сил, статически эквивалентный заданным объемным силам;
FS – глобальный вектор узловых сил, статически эквивалентный заданным поверхностным силам.
9.15.2.
Структура глобальной матрицы жесткости
Матрица жесткости конечно-элементной модели формируется путем сложения по определенным правилам элементных матриц жесткости:
,
(9.194)
где ae - матрицы кинематических связей.
Эта процедура называется сборкой или ансамблированием.
Рассмотрим процесс сборки (9.194) на простом примере, чтобы понять закономерности формирования глобальной системы алгебраических уравнений. Это поможет лучше понять другие более эффективный алгоритмы построения матрицы K, рассматриваемые в специальной литературе по МКЭ.
Пусть сетка образована двумя четырех-узловыми линейными изопараметрическими элементами (Рис. 9.76). Глобальное
число узлов равно шести, при этом каждый узел имеет свой уникальный глобальный
номер от 1 до 6. Введем локальную естественную систему координат 
на каждом элементе. Пронумеруем узлы на
каждом элементе в соответствии с ориентацией локальной системы координат от 1
до 4. Таким образом, получаем, что каждому узлу ставится в соответствие два
номера: локальный 
и глобальный 
, где 
- глобальное число узлов конечно-элементной сетки.
Данное соответствие нумерации узлов помогает легко сформировать матрицы кинематических связей ae, которые, по определению (9.53), связывают глобальный вектор узловых перемещений U с каждым элементным вектором узловых перемещений:
(9.195)
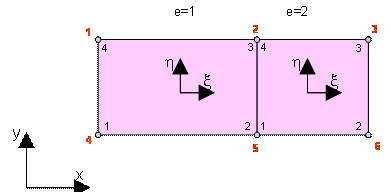
Рис. 9.76. Конечно-элементная сетка, образованная двумя четырех-узловыми
линейными изопараметрическими элементами.
Показаны локальные и глобальная системы координат, локальная нумерация узлов на каждом элементе от 1 до 4 и глобальная нумерация по всей сетке от 1 до 6.
В данном случае имеем:
,
(9.196)
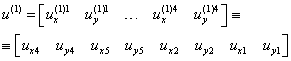, (9.197а)
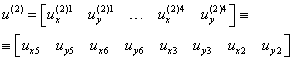. (9.197б)
Сравнивая выражения (9.197а) и (9.197б) с (9.196) и принимая во внимание, что должны выполняться уравнения (9.175), получим для каждого элемента выражения матриц кинематических связей:
, (9.198а)
,
(9.198б)
где 1 - единичная матрица размерности 2x2;
0 – нулевая матрица размерности 2x2:
, 
. (9.199)
Вычислим первое слагаемое в сумме (9.194):
, (9.200)
где k1(ij) - матричный блок размерности 2x2, определяемый формулами (9.159 и 9.172).
Перемножив матрицы в формуле (9.200), получим «отображение» элементной матрицы первого элемента на «плоскость» глобальной матрицы:
(9.201)
Сразу заметим, что положение блока k1(ij) в матрице K(1) определяется соответствующими глобальными номерами. Так, например, блок k1(12) имеет локальные номера i=1 и j=2. Узлы с локальными номерами i=1 и j=2 на первом элементе имеют глобальные номера I=4 и J=5. В результате блок k1(12) перемещается на 4-ю строку, 5-й столбец глобальной матрицы K(1).
Аналогично рассуждая, вычислим второе слагаемое в сумме (9.194):
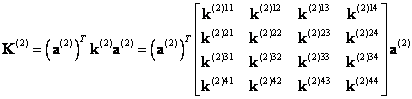(9.202)
После перемножения получим:
(9.203)
Остается сложить матрицы (9.201) и (9.203), чтобы получить искомую глобальную матрицу жесткости рассматриваемой конструкции:
(9.204)
9.15.3.
Структура глобального вектора узловых сил
Глобальный вектор узловых сил формируется аналогичным образом:
(9.205)
Пусть, например, рассмотренная выше конструкция находится под действием сил тяжести. Тогда будут сформированы два элементных вектора объемных сил в узлах:
, (9.206а)
,
(9.206б)
где 
- матричный блок
размерности 2x1, состоящий из компонент вектора силы в узле i элемента е
(9.177, 9.181).
Подставляя выражения (9.206а, б) в (9.205) с учетом вида матриц кинематических связей (9.198а, б), получим глобальный вектор узловых сил:
(9.207)
Анализируя выражения (9.204) и (9.207), заметим, что складываются только те элементы матрицы жесткости или вектора нагрузки, которые относятся к общим узлам сетки. Кроме того, если узлы относятся к разным элементам и имеют различные глобальные номера, то соответствующие блоки матрицы жесткости равны нулю. Это является следствием локальности функций формы, благодаря чему имеет место влияние узлов друг на друга только в пределах данного конечного элемента. Влияние же на другие узлы происходит опосредованно через общие узлы между элементами. Это приводит к разреженной структуре глобальной матрицы жесткости с диагональным преобладанием.
9.15.4.
Решение глобальной системы конечно-элементных уравнений
После того как глобальная система конечно-элементных уравнений (9.193) сформирована, необходимо разрешить ее относительно глобального вектора степеней свободы модели с тем, чтобы определить все перемещения узлов конструкции. Существует большое количество разработанных методов, алгоритмов и готовых программ для решения систем линейных алгебраических уравнений, наиболее известным из которых является метод исключения Гаусса, состоящий в приведении исходной матрицы к треугольному виду.
Однако при решении и выборе метода расчета систем конечно-элементных уравнений необходимо принимать во внимание ряд свойств СЛАУ и, в частности, свойств матрицы жесткости K:
При расчете реальных механических конструкций СЛАУ МКЭ может достигать десятков и сотен тысяч уравнений. Современный рекорд формирования и решения СЛАУ МКЭ равняется 50 миллионам уравнений. Заметим здесь же, что если задача отлична от статической линейной, то необходимое число решений системы может быть сколько угодно большим, например, при расчете динамики конструкции. К счастью, сложности, связанные с большим количеством уравнений, частично компенсируются другими свойствами матрицы жесткости, что и делает МКЭ таким привлекательным с точки зрения инженерных расчетов.
Матрица жесткости симметрична:
(9.208)
Хотя мы специально не доказывали свойство (9.208), его легко проверить на примере (9.204), если учесть, что элементные матрицы жесткости симметричны, т.е.:
K(e)ij = k(e)ji (9.209)
Матрица жесткости является положительно-определенной, что означает, что квадратичная форма:
(9.210)
при любых 
.
Свойства положительной определенности и симметрии матрицы являются необходимыми для построения или применения известных более эффективных алгоритмов решения СЛАУ, чем метод исключения Гаусса.
Матрица является ленточной и редко-заполненной, что означает, что ненулевые элементы матрицы сосредоточены вблизи главной диагонали. Следовательно, для эффективного использования машинной памяти и расчета достаточно хранить только ненулевые элементы ленты матрицы. Размер ленты, т.е. число ненулевых элементов в ней, существенно зависит от конкретного вида конструкции и способа нумерации узлов. В среднем можно принять, что размер ленты равен приблизительно числу уравнений, входящих в систему.
Большие матрицы могут быть плохо-обусловленными. Число обусловленности равно отношению максимального собственного числа матрицы к минимальному и существенно влияет на устойчивость и точность численного решения. Число обусловленности сильно зависит размеров и формы конечных элементов. Поэтому необходимо внимательно следить за построением сетки и избегать больших градиентов размеров элементов, а также слишком больших или слишком малых углов между сторонами элементов.
9.15.5.
Метод треугольной факторизации Холецкого
Метод треугольной факторизации Холецкого является одним из самых популярных прямых методов решения СЛАУ МКЭ, поскольку он учитывает все положительные свойства матрицы жесткости, отмеченные выше. К сожалению, он применим, как и все прямые методы, к относительно небольшим системам уравнений (до 104 уравнений). Связано это с внутренней машинной проблемой: при любой реальной точности хранения чисел и операций умножения и деления, достижимой на данном компьютере, ошибка вычислений, тем не менее, накапливается и при большом числе операций может стать катастрофической. Единственным выходом в данной ситуации является применение итеративных методов решения СЛАУ, свободных от данной проблемы.
Итак, рассмотрим вкратце алгоритм Холецкого. Подробное описание и расчетные формулы есть во всех книгах по вычислительной математике.
Треугольное разложение матрицы K. Представим матрицу K в виде произведения трех матриц:
, (9.211)
где L - нижняя треугольная матрица с единицами на главной диагонали;
D - диагональная матрица, причем все 
.
Прямой ход. Решаем систему линейных
алгоритмических уравнений в три этапа. Обозначим 
и решим СЛАУ:
(9.212)
В результате найдем вектор Z.
Масштабирование. Решаем СЛАУ с
диагональной матрицей, обозначив 
:
(9.213)
Обратная подстановка. Последний шаг – вычисляем искомый вектор перемещений путем решения СЛАУ с нижней диагональной матрицей:
(9.214)
9.15.6.
Вычисление напряжений
После решения СЛАУ определены все узловые перемещения. Теперь с помощью интерполирующих соотношений можно определить деформации и напряжения в любой точке конечного элемента по формулам (9.31, 9.34):
(9.215)
(9.216)
Заметим, что точки 
могут быть любыми на
элементе. Однако, для повышения эффективности и точности вычислений, обычно
деформации и напряжения определяются в точках квадратур Гаусса, а затем
экстраполируются в узлы элемента.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
