Главная
9.16.
Алгоритм МКЭ для трехмерной задачи теории упругости.
9.16.1.
Введение
Динамическая задача линейной теории вязко-упругости (Рис. 9.77) описывается хорошо известной
системой тензорных уравнений в заданном объеме сплошной среды V
с граничными условиями кинематического или силового типа на ее поверхности 
:
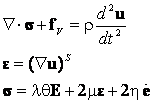, (9.217)
где 
- тензора напряжений и
деформаций;
e - девиатор
тензора деформаций: 
;
E - единичный тензор;
u=u(r,t) - вектор перемещений, зависящий от времени t и радиуса вектора точек сплошной среды r;
fv=fv(r,t) - вектор заданных объемных сил, зависящий от времени t и радиуса вектора точек сплошной среды r;
, 
, 
- коэффициенты
Ламе и вязкость материала;
- плотность;
- объемная деформация;
- дифференциальный оператор Гамильтона.
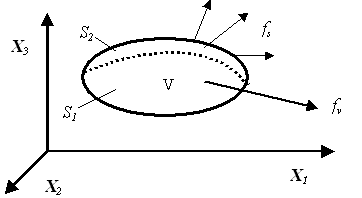
Рис. 9.77. Постановка общей задачи теории упругости.
Коэффициенты Ламе, используемые в записи
обобщенного закона Гука, связаны с техническими константами материала: модулем
упругости Е, модулем сдвига G и коэффициентом Пуассона 
следующими
соотношениями:
Приведенная дифференциальная постановка задачи теории упругости эквивалентна вариационной постановке в виде принципа минимума потенциальной энергии Лагранжа или принципа возможных перемещений:
(9.218)
где 
- вектор
возможных перемещений точек сплошной среды;
- вектор сил инерции;
- вариация
потенциальной энергии деформации тела:
(9.219)
Интегралы слева представляют собой работы внешних объемных и поверхностных сил, а также сил инерции на возможных перемещениях.
9.16.2.
Алгоритм
1. Первым шагом общего алгоритма МКЭ является разбиение упругой области на ряд непересекающихся подобластей простой формы, называемых конечными элементами (Рис. 9.78). Во многих конечно-элементных программах этот шаг носит название генерации конечно-элементной сетки.
Рис. 9.78. Разбиение тела на конечные элементы.
Согласно процедуре конечно-элементной дискретизации области, формируются элементные вектора, содержащие в определенной последовательности координаты узлов соответствующего конечного элемента:
и глобальный вектор координат узлов, содержащий координаты всех узлов сетки:
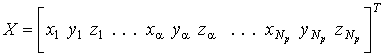
Каждый элементный вектор связан с глобальным вектором с помощью алгебраического матричного соотношения:
,
где 
представляет собой
матрицу связи, состоящую из нулей и единиц.
Наконец, координаты любой внутренней точки p элемента могут быть определены с помощью интерполяционного соотношения через заданные координаты узлов конечного элемента:
,
где 
- матрица
интерполирующих функций или, согласно другой терминологии, функций формы. Вид
матрицы и образующих ее функций существенно зависит от типа используемого
конечного элемента.
2. Вторым важным этапом общего алгоритма МКЭ является аппроксимация искомых функций – функции перемещений при использовании вариационного принципа Лагранжа. В случае так называемых изопараметрических конечных элементов формулы, записанные выше, легко преобразуются для описания неизвестных перемещений.
В частности, имеем:
элементный вектор перемещений:
,
где 
глобальный вектор перемещений:
,
соотношение между элементными и глобальным векторами:
,
перемещение в любой внутренней точке p конечного элемента:
,
где
,
Отметим, что в случае изопараметрического конечного элемента имеют место простые соотношения:
.
3. Основным и наиболее трудоемким этапом в методе конечных элементов является формирование системы алгебраических уравнений, следующих из соответствующего вариационного принципа, в рассматриваемом случае - из принципа минимума потенциальной энергии Лагранжа или эквивалентного ему принципа возможных перемещений. В качестве альтернативного подхода к выводу глобальной системы алгебраических конечно-элементных уравнений может быть предложен известный из теории приближенных решений математический метод взвешенных невязок. Обладая несомненной универсальностью, метод взвешенных невязок, тем не менее, требует дополнительных знаний из общей теории приближенных методов, а также требует большего числа математических операций при выводе алгоритма. Поэтому в настоящем изложении основ МКЭ мы воспользуемся более очевидным для инженера-механика принципом возможных перемещений.
Согласно общему подходу конечно-элементной дискретизации, преобразуем алгебраические и дифференциальные соотношения, связывающие непрерывные векторные и тензорные переменные, к матричной форме между узловыми векторами.
3.1. Кинематическое соотношение.
Тензорное соотношение, линейно связывающее кинематические переменные упругого движения: тензор деформаций и вектор перемещений (второе уравнение в системе 9.217), преобразуется к матричному виду следующим образом:
,
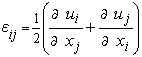
где
есть
матричный вектор, образованный шестью независимыми компонентами тензора
деформаций,
- так называемая матрица градиентов, состоящая
из частных производных от интерполирующих функций,
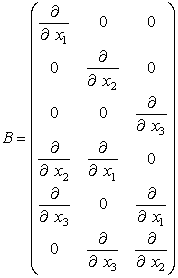
B - символическая матрица, образованная частными производными по пространственным координатам:
3.2. Определяющее соотношение, задающее связь деформаций и напряжений в точке сплошной среды (третье уравнение в системе 9.217).
В качестве определяющего соотношения идеальной упругости рассмотрим обобщенный закон Гука, задающий линейную связь напряжений с деформациями. В матричной форме закон Гука принимает следующий вид:
,
где
есть
матричный вектор, образованный шестью независимыми компонентами тензора
напряжений,
D
- матрица упругих модулей:
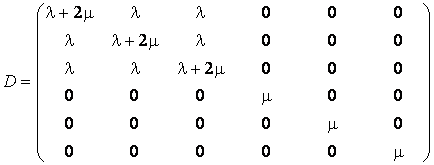
В случае кусочно-однородной сплошной среды различным элементам соответствуют материалы с различными упругими постоянными, и следовательно, матрица D будет существенным образом зависеть от номера элемента. В общем случае непрерывного изменения упругих постоянных, характерного для описания как твердых, так и мягких тканей, может быть предложен приближенный подход, сводящий непрерывно-неоднородную область к большому числу конечных элементов, описываемых осредненными в пределах элемента матрицами упругости. Однако, возможен и другой вариант, при котором упругие модули считаются функциями координат, что приводит к необходимости вычисления более сложных интегралов по объему конечного элемента как будет ясно из дальнейшего.
Отметим, что в данном случае мы рассмотрели только вариант изотропной сплошной среды. Матрица упругих модулей в общем случае анизотропной среды выводится аналогичным образом из обобщенного закона Гука, включающего в себя большее число независимых упругих констант.
3.3. Формирование глобальной системы алгебраических уравнений.
Формирование глобальной системы алгебраических уравнений осуществляется путем преобразования исходного вариационного соотношения. В данном случае мы используем уравнение принципа возможных перемещений (9.218).
Проведем предварительные преобразования и вычислим:
Вариация вектора перемещений:
Вариация вектора деформаций:
Вариация потенциальной энергии деформации тела (9.219):
,
где
- элементная
матрица жесткости
- глобальная
матрица жесткости
Элементарная работа внешних объемных и поверхностных сил на возможных перемещениях:
,
где
- элементный
вектор объемных узловых сил
- элементный
вектор поверхностных узловых сил
- глобальный
вектор объемных узловых сил
- глобальный
вектор поверхностных узловых сил
Заметим, что записанные выше элементные и глобальные вектора узловых сил статически эквивалентны объемным и поверхностным силам, заданным на данном элементе или во всем объеме тела.
Наконец, используя основную формулировку принципа возможных перемещений (9.218), согласно которой виртуальная работа внешних сил равна вариации потенциальной энергии деформации тела:
,
(9.220)
и подставляя затем в данное равенство полученные выше выражения элементарной работы и вариации энергии деформации, сравнивая выражения слева и справа, получим следующее матричное уравнение:
(9.221)
Данное выражение является основным разрешающим соотношением метода конечных элементов и представляет собой систему линейных алгебраических уравнений относительно узловых перемещений. После корректного наложения заданных кинематических граничных условий уравнение может быть решено одним из известных численных методов, применяемых в теории решения больших систем с разреженными матрицами.
4. После определения глобального вектора узловых перемещений:
могут быть вычислены деформации и напряжения в любой точке каждого элемента по записанным выше формулам, а, следовательно, будут получены значения деформаций и напряжений в произвольных точках тела:
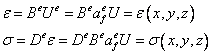
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
