Главная
9.17.
Современные программные средства конечно-элементного анализа
9.17.1.
Программные системы
Развитие метода конечных элементов обусловлено взаимосвязью трех факторов: наличием высокопроизводительной вычислительной техники; разработкой математических моделей исследуемых явлений, адекватных реальным процессам с достаточной степенью точности; особенностями самого метода [26].
Первые программные комплексы, в которых реализован метод конечных элементов, были разработаны в 60-х годах. К ним относятся STRUDL-II, SAP-IV, NONSAP, ASKA, NASTRAN, SESAM-69 и другие [41]. Появлению этих универсальных программных систем в силу особенностей метода конечных элементов предшествовало создание высокопроизводительных электронно-вычислительных машин, таких, например, как IBM-370. Начиная с конца 70-х годов в СССР появилось несколько десятков программных комплексов для разных ЭВМ, в которых был реализован МКЭ. К их числу относятся МИРАЖ [13], МОРЕ [27], КАСКАД-2 [28], ПРОЧНОСТЬ-75 [17], МКЭ/20 [10], МАРС [11], ПАРСЕК [7], ЛИРА [14], СПРИНТ [34], FEA [4] и ряд других программ [33].
В США и ряде других стран дальнейшее развитие МКЭ и необходимость в проведении расчетов конструкций на прочность также способствовали дальнейшему развитию уже созданных программных комплексов и разработке новых. Были разработаны сотни программных комплексов, предназначенных для приближенного решения самых разнообразных задач не только из области механики деформируемого твердого тела, но и из таких областей как гидродинамика, акустика, электротехника и т.д. Наибольшее распространение из них получили [40]: ABAQUS, ADINA, ASKA/DYNAN, ANSYS [2], MARC, MSC/NASTRAN [35], EUFEMI, COSMOS, HERCULE, MODULEF, SAP-7, LS-DYNA.
Отметим, что разработка программных комплексов является дорогостоящим делом. Поэтому, как правило, организации и фирмы – собственники разработанных программ, рассматривают их как коммерческий научно-технический продукт. Регулярно печатаемые обзоры существующих комплексов программ и их характеристик, сведения о программах в отраслевых фондах алгоритмов и программ позволяют пользователям программной продукции целенаправленно выбирать необходимые для их деятельности программы расчета.
У каждой программы есть свои сильные и слабые стороны при расчете конкретной конструкции. Выбор программы расчета зависит от подготовленности пользователя в своей научной области, типа решаемой задачи, типа доступной ЭВМ, размерности задачи и других факторов.
К критериям, помогающим сделать выбор, следует отнести следующие факторы:
- программа широко используется;
- в программе используются новейшие научные достижения;
- программа коммерчески вполне доступна;
- имеется подробная и понятная документация.
Ознакомление с программной документацией и доступной литературой с описанием программы и ее элементов позволяют сделать окончательный вывод о целесообразности выбора программного комплекса.
Для МКЭ характерны особенности, которые следует учитывать при выборе и разработке программы расчета. Такими особенностями являются большие объемы исходных данных, промежуточных и окончательных результатов расчета. Поэтому расчет по МКЭ состоит из трех основных этапов:
- разработка расчетной конечно-элементной схемы и подготовка исходных данных;
- проверка самого расчета;
- обработка результатов расчета.
На рис. 9.79 приводится одна из возможных схем организации расчета по МКЭ [33]. Каждый этап является самостоятельной задачей. На первом этапе самое существенное заключается в создании начальной конечно-элементной расчетной модели, исходя из инженерной интуиции о поведении конструкции. В последствии эта модель может корректироваться на основе анализа результатов расчета. Корректировка модели может выполняться и программным путем, если такая возможность реализована в используемом программном комплексе. Подготовка исходных данных осуществляется, как правило, с помощью программ генераторов сеток конечных элементов, образующих блок подготовки данных.
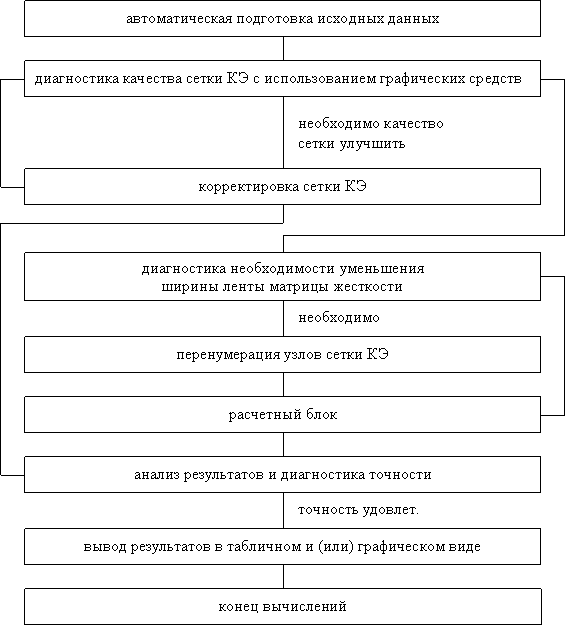
Рис. 9.79. Схема организации расчета по МКЭ.
Проведение расчета (этап 2) осуществляется расчетным блоком, в котором используется тот или иной алгоритм расчета методом конечных элементов. Как правило, расчетный блок состоит из ряда программных модулей, каждый из которых выполняется на определенном шаге алгоритма. В простейшем случае программной реализации МКЭ для линейной статической краевой задачи теории упругости расчетный блок содержит следующую последовательность шагов:
- ввод исходных данных (например, подготовленных программой-генератором в отдельном файле);
-вычисление матриц жесткостей конечных элементов;
- формирование глобальной матрицы жесткости полной структуры;
- формирование глобального вектора нагрузок;
- решение системы линейных алгебраических уравнений;
- вычисление перемещений узлов сетки конечных элементов, деформаций и напряжений в произвольных точках конечных элементах.
На различных шагах расчетного блока включаются проверки правильности исходных данных и результатов промежуточных вычислений (диагностика ошибок), программные модули выбора сочетаний нагрузок, действующих на конструкцию, определение площади сечений арматуры в железобетонных конструкциях и другие. Диагностика ошибок на этапе выполнения программы является важной, так как при своевременном обнаружении ошибки прекращаются вычисления, что приводит к экономному использованию ресурсов ЭВМ.
Эффективное использование ЭВМ достигается также за счет разработки специальных методов решения стандартных математических задач, учитывающих специфику МКЭ, и, в первую очередь, ленточность и разреженность матрицы жесткости расчетной модели конструкции.
Расчет напряженно-деформированного состояния конструкции в рамках линейной теории упругости при действии на нее статических нагрузок сводится к решению системы линейных алгебраических уравнений. В конечно-элементных комплексах программ используются разнообразные методы решения больших систем уравнений.
Различные варианты метода Гаусса реализованы в программах ADINA (блочный метод Гаусса), ASKS, SAP-7 (ленточный метод Гаусса), NASTRAN (LTDL - декомпозиция). Эффективным является фронтальный метод, реализованный в программах ABAQUS, ANSYS и др. Методы суперэлементов и редукции базиса позволяют существенно сократить время вычисления [18]. Эффективными являются также итерационные методы [1].
Расчет собственных колебаний конструкции выполняется методами: итерации в подпространстве (SAP-7), вычисления корней характеристического определителя (NASTRAN), Хаусхолдера с использованием метода Якоби (ASKA), Гивенса и QR-метода (NASTRAN), Hiber-Hughes (ABAQUS), Ланцоша (PKM). При расчет динамического отклика используются методы: представления решения в виде суперпозиции форм собственных колебаний, шаговые – Вилсона, Ньюмарка (ABAQUS, ADINA, SAP-7, NASTRAN). Решение геометрически и физически нелинейных задач осуществляется, как правило, итерационными методами, основу которых составляет метод Ньютона-Рафсона в сочетании с шаговыми методами (ABAQUS, ADINA, NASTRAN, ANSYS, LASTRAN и др.) [33].
Следует отметить, что принцип модульности программирования, использованный в программных комплексах, позволяет создавать как универсальные вычислительные программы, так и промышленные для решения узкого класса задач. На первых этапах освоения МКЭ разрабатывались в основном промышленные вычислительные программы. Они эффективны, если решается большое количество вариантов однотипных задач, либо выполняется большой объем вычислений для качественного и количественного исследования явлений, связанных с новой постановкой задачи. Тенденция развития вычислительной техники, приведшая к созданию персональных ЭВМ и новых информационных технологий, оказала влияние на разработку программного обеспечения МКЭ [6]. Программные комплексы по МКЭ активно используются в системах автоматизированного проектирования, базирующихся на персональных ЭВМ (AutoCAD/MechanicalDesktop, Pro-Engineer).
9.17.2.
Краткие характеристики некоторых программных комплексов
Современные комплексы программ, в которых используется МКЭ, позволяют получать приближенные численные решения при расчете конструкций на статические и динамические нагрузки для широкого класса материалов с различными механическими характеристиками и поведением. Расчет конструкций на статические нагрузки может производиться с учетом физической и геометрической нелинейности, температурных полей, взаимодействия с другими средами (например, с жидкостью). Производится расчет критических нагрузок, при которых конструкция или ее элементы теряют устойчивость, поведения конструкции после потери устойчивости. МКЭ позволяет также определить нагрузки, при которых происходит разрушение конструкции. Учитываются такие свойства материала как анизотропность, нелинейная упругость, пластичность, текучесть. Учитываются виды геометрической нелинейности: большие деформации и большие перемещения. Основными динамическими задачами являются: расчет собственных колебаний конструкции; динамический отклик на нагрузку, зависящую от времени; распространение волн [33].
Ниже в таблице 9.2. приводятся сравнительные характеристики наиболее распространенных комплексов программ описанных в работе [40].
Таблица 9.2. Краткие характеристики наиболее распространенных комплексов программ МКЭ
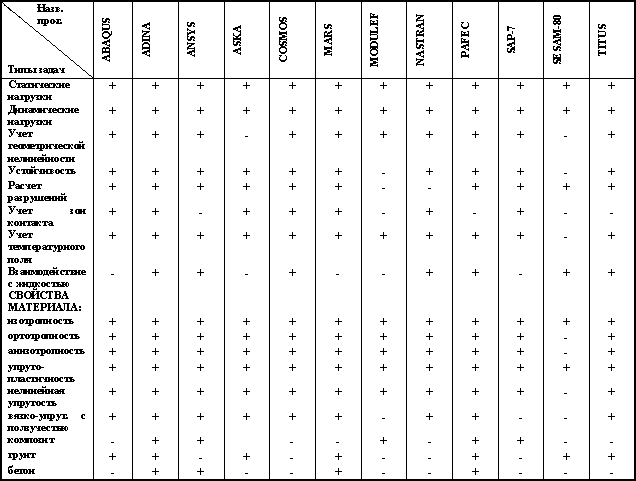
Приведенные в таблице комплексы программ являются универсальными. Опишем подробно один из комплексов, например, ABAQUS [33]. Этот программный комплекс разработан относительно недавно для расчета новых прогрессивных конструкций. Разработчики этого комплекса (Hibbit, Karlson, Sorensen) сохранили простоту и эффективность расчета для линейных задач при учете сугубо нелинейных эффектов – геометрических и физических. Комплекс программ позволяет производить расчет стационарных и нестационарных температурных полей, их влияния на напряженно-деформированное состояние конструкции, ее устойчивость, оценивать трещинообразование, учитывать зоны контакта с трением, учитывать процессы фильтрации жидкости в грунтах. Расчет на нагрузку, зависящую от времени, производится с учетом предварительной нагруженности конструкции. Обширная библиотека конечных элементов, разнообразный набор характеристик материала (линейно упругий, гиперупругий, полностью несжимаемый с зависимостью свойств от температуры) и моделей его поведения (общий упругопластический с изотропным и кинематическим упрочением, упруговязкопластический, специальные законы ползучести, объемное упрочнение) позволяют решать достаточно широкий класс задач.
Следует отметить, что выбор модели поведения материала является определяющим для достоверности рассчитанного напряженно-деформированного состояния конструкции. Например, в программе MARS используется 30 моделей поведения материала (вязкоупругость по Максвеллу или Кельвину; пластичность по критерию Мизеса или Мора, или Кулона, с изотропным или (и) кинематическим упрочением по теории ассоциированного или неассоциированного течения, с учетом температуры; ползучесть по закону Мизеса, чисто объемная или чисто девиаторная ползучесть, анизотропность при упругопластической ползучести: вязкопластичность, несжимаемость или почти несжимаемость, большие деформации по закону Муни-Ривлина и т.д.).
Программы промышленного назначения предназначены для расчета узкого класса конструкций. Примером программы промышленного назначения является программа BERSAFE, разработанная для расчета элементов конструкций атомной энергетики. В этой программной системе для расчета напряженно-деформированного состояния используются специальные законы ползучести бетона и графита, поведения скальной породы. Другим примером программы промышленного назначения служит программа EFESYS, предназначенная для расчета плотин и морских сооружений с учетом связанности процессов фильтрации и напряженно-деформированного состояния. Программный комплекс ПОЛИФЕМ-87 предназначен для расчета на сейсмические воздействия сооружений как пространственных систем. Отметим, что универсальные и промышленные комплексы программ не могут быть эффективно использованы для изучения МКЭ. Для изучения различных аспектов МКЭ разработаны специальные учебные программные комплексы [37]. Для решения различных задач биомеханики широко используются коммерческие универсальные комплексы ABAQUS, ANSYS, MARS, NASTRAN, а также разрабатываются специализированные программы, реализующие метод конечных элементов, для повышения эффективности решения той или иной конкретной задачи [39].
9.17.3.
Дополнительная литература
1. Абрамов Н.Н., Беркун В.Б., Кучеренко В.В., Перекальский В.М. Эффективные итерационные алгоритмы решения тепловых задач: Учебное пособие – М.: МИСИ, 1987. 67 с.
2. Басов К.А. ANSYS в примерах и задачах. М.: КомпьютерПресс, 2002. 224 с.
3. Бердичевский В.Л. Вариационные принципы механики сплошной среды. М.: Наука, 1982, 448 с.
4. Боровков А.И. Программный комплекс конечно-элементного анализа FEA // Аннотированный каталог учебных программных средств. Вып.3. СПб: СПбГТУ, 1995. С.100-102.
5. Бреббия К., Телес Ж., Вроубел Л. Методы граничных элементов. М.: Мир, 1987. 348 с.
6. Бурман Я.З., Салахов Р.Р. О реализации МКЭ на персональных ЭВМ. Прикладные проблемы информатики, No1, 1989.
7. Бурышкин М.Л., Гордеев В.Н. Эффективные методы и программы расчета на ЭВМ симметричных конструкций. Киев: Будивельник, 1984.120 с.
8. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Аналитическая механика. М.: Наука, 1984. 452с.
9. Васидзу К. Вариационные методы в теории упругости и пластичности. М.: Мир, 1987. 542 с.
10. Вилипыльд Ю.К., Лайгна К.Ю., Кала Т.Н. Расчет стержневых и пластинчатых систем по методу конечных элементов МКЭ/20. Таллинн, 1979. 115 с.
11. Галкин Д.С., Галкина Н.С., Гусак Ю.В. Многоцелевая автоматизированная расчетная система МАРС. Сб.: Комплексы программ математической физики. – Новосибирск, 1984.
12. Галлагер Р. Метод конечных элементов. Основы. М.: Мир, 1984. 428 с.
13. Городецкий А.С. Программа МИРАЖ для статического расчета конструкций методом конечных элементов. Автоматизация проектирования как комплексная проблема совершенствования проектного дела в стране: Сб. трудов всесоюзной научной конференции. М., 1973.
14. Городецкий А.С., Здоренко В.С. Типовая проектирующая подсистема ЛИРА для автоматизированного проектирования несущих строительных конструкций. Сб.: Системы автоматизированного проектирования объектов строительства. Вып.1, 1982.
15. Зенкевич О. Метод конечных элементов в в технике. М.: Мир, 1975. 536 с.
16. Зенкевич О., Морган К. Конечные элементы и аппроксимация. М.: Мир, 1986. 318 с.
17. Исаханов Г.В., Кислоокий В.Н., Сахаров А.С., Синявский А.Л. Система математического обеспечения расчетов пространственных конструкций // Проблемы прочности, No11, No12, 1978.
18. Калугин О.Ю., Кучеренко В.В., Попов В.А., Щукин О.И. Методика использования макроэлементов для решения на ЭВМ пространственных задач большой размерности. Учебное пособие. – М.: МИСИ, 1987. 105 с.
19. Лехницкий С.Г. Теория упругости анизотропного тела. М.: Наука, 1977. 282 с.
20. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики. Т. 1, 2. М.: Наука, 1982, 1983. 352 с., 640 с.
21. Лурье А.И. Теория упругости. М.: Наука, 1980. 936 с.
22. Лурье А.И. Нелинейная теория упругости. М.: Наука, 1980. 512 с.
23. Маслов Л.Б. Пpименение методов гpаничных и конечных элементов для анализа концентpации напpяжений в двумеpных и тpехмеpных задачах теоpии упpугости. Дис. … канд. техн. наук. ЛГТУ, 1992. 258 с.
24. Маслов Л.Б. Численные методы для pешения задач теоpии упpугости: Методическое пособие / Иван. гос. энеpг. ун-т.- Иваново, ИГЭУ, 1999. - 28с.
25. Маслов Л.Б., Козлов М.В. Конечно-элементный программный комплекс “МЕХАНИКА” - приложение в инженерном деле и биомеханике // Вестник Иван. гос. энеpг. ун-та. - Иваново, ИГЭУ, 2002. - No 2. - С. 23-28.
26. Молчанов И.Н., Николенко Л.Д. Основы метода конечных элементов. Киев: Наукова Думка, 1989. 272 с.
27. Никольский М.Д., Чернева И.М., Безперстова Н.Ф.и др. Комплекс программ МОРЕ для расчета сооружений по методу конечных элементов. В книге: Экспериментальные и теоретические исследования по механике твердого деформируемого тела. Сб. трудов ЛИИЖТ. – Л.: ЛИИЖТ, 1978.
28. Постнов В.А. Проблемы автоматизации метода суперэлементов. Программный комплекс КАСКАД-2. Сб.: Применение численных методов в строительной механике. – Л.: Судостроение, 1976.
29. Работнов Ю.Н. Механика деформируемого твердого тела. М.: Наука, 1988. 712 с.
30. Самарский А.А. Введение в численные методы.- М.: Наука, 1987. - 459с
31. Тимошенко С.П., Янг Д.Х., Уивер У. Колебания в инженерном деле. М.: Машиностроение, 1985. 472 с.
32. Флетчер К. Численные методы на основе метода Галеркина. М.: Мир, 1988. 352с.
33. Хечумов Р.А., Кепплер Х., Прокопьев В.И. Применение метода конечных элементов к расчету конструкций. М.: Изд-во Ассоциации строительных вузов, 1994. 353 с.
34. Шапошников Н.Н. Система прочностных расчетов по МКЭ СПРИНТ для ЕС ЭВМ. Сб.: Практическая реализация численных методов расчета инженерных конструкций. – Л.: Знание, 1981.
35. Шимкович Д.А.
Расчет конструкций в MSC/NASTRAN for Windows. ДМК, 2001. 448 с.
36. ANSYS Basic Analysis Procedures Guide. 1998.
37. Dahlblom O., Peterson A., Peterson H.
CALFEM – a program for computer-aided learning of the finite element metod. Eng.Comput.,vol.3,
N02,1986.
38. Felippa C., Introduction to Finite Element
Methods,
39. Middleton, J., Jones, M.L., Eds., Computer Methods in Biomechanics
and Biomedical Engineering. Gordon & Breach Science Publishers, 1998.
40. Niku-Lari A. Structural analysis system, (Sofware-Hardware, Capability – Compability
– Aplications). Pergamon
Press,vol.1-3,1986.
41. Pilkey W., Saczalski
K.,Schaeffer H. Structural Mechanics Computer
Programs, Surveys, Assessments, and avialability. – Univertsity Press of
42. Zienkiewicz O.C., Taylor Robert L.,
43. Zienkiewicz O.C., Taylor Robert L.,
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21