Главная
9.20.
Общая схема алгоритма МГЭ для решения плоских задач теории упругости
Первый
этап – ввод исходных данных.
Данный этап, который является первым шагом выполнения любой инженерной программы, основан на концепции макроэлементов, позволяющей значительно сократить и упростить процедуру ввода чисел. Применительно к плоской задаче теории упругости она состоит в том, что вся граница исследуемой упругой области разбивается на простые линии, выбираемые из библиотеки макроэлементов. Такими линиями могут быть отрезок прямой, часть параболы, дуга окружности или целая окружность. Это так называемые графические примитивы, с помощью которых достаточно легко смоделировать границу любого плоского тела с высокой точностью.
Следовательно, минимальная вводимая информация должна содержать количество и тип макроэлементов, число разбиений каждого макроэлемента на граничные элементы, тип граничных условий, координаты узлов макроэлементов и значения граничных перемещений и усилий в узлах макроэлементов.
Второй этап – дискретизация границы области и аппроксимация граничных условий.
Для наиболее точного описания неизвестных
заранее полей перемещений и напряжений введенные макроэлементы разбиваются на ряд
граничных элементов Ге
с помощью подпрограммы, носящей название «автоматический генератор данных». В
результате разбиения формируются глобальные векторы узлов границы 
, узловых значений граничных перемещений 
и усилий 
.
Координаты любой внутренней точки 
линейного элемента Ге,
представленного в виде отрезка прямой линии, определяются в соответствии с
общими соотношениями (9.228) и конкретным видом функций формы (9.235):
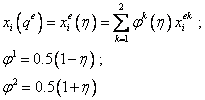. (9.237)
Аналогично, интерполяционные формулы (9.229)
определят значения перемещений и усилий в любой внутренней точке граничного элемента Ге:
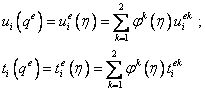. (9.238)
Таким образом, глобальные векторы 
будут состоять из
узловых значений 
, 
, 
, где i=1,2; k=1,2; e=1,…,N.
Третий
этап – построение матриц влияния и формирования СЛАУ.
Рассмотрим дискретизованное
ГИУ (9.231). В случае двумерной области дифференциал границы 
представляет собой
бесконечно малый отрезок, длина которого
.
Используя соотношения (9.237), вычислим
.
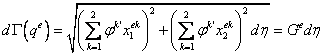Величина 
представляет собой
якобиан преобразования от глобальной системы координат к локальной координате 
. Его легко вычислить в случае линейных функций форм. В самом
деле,
.
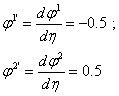Следовательно,
,
где 
- длина граничного
элемента Ге
(рис. 20.2).
Таким образом, интегралы по граничному
элементу Ге
в глобальной системе координат 
в выражении (9.230)
преобразуются к интегралам по локальной координате и ГИУ (9.230) после
подстановки в него интерполяционных соотношений (9.238) примет вид:
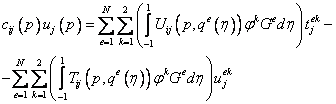. (9.239)
Согласно методу коллокаций
совместим последовательно точку 
со всеми узлами
границы:
При этом глобальный размер узла 
однозначно
определяется номером граничного элемента 
и локальным номером 
узла на элементе. Тогда ГИУ (9.239) примет вид системы 
уравнений:
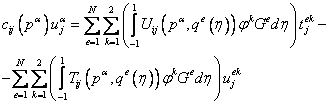. (9.240)
Эта система алгебраических уравнений
относительно переменных 
, 
представляет собой
развернутую запись матричного уравнения (9.234) для двумерной области 
.
Из соотношений (9.240) видно, что глобальные
матрицы влияния 
и 
состоят из
элементарных интегральных выражений, образующих матричные блоки 
, 
, где глобальный номер узла 
определяется через
номер элемента и локальный номер узла - 
:
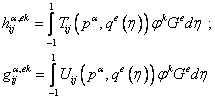, (9.241)
где вид ядер 
, 
задан выражениями
(9.236).
Рис. 9.85. Граница области с угловой точкой.
Матрицы 
для любой точки 
имеют простой вид:
в том случае, если граница в окрестности
точки гладкая.
Если точка угловая, то выражение матрицы 
имеет вид:
,
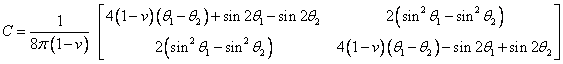где 
- углы, показанные на
рис. 9.85.
Таким образом, на данном этапе, являющемся
наиболее сложным, вычисляются интегралы (9.241) и формируется СЛАУ (9.240).
После наложения граничных условий (9.224а), т.е. разбивки глобальных векторов и на известную часть V, P и неизвестную часть 
, СЛАУ (9.240) преобразуется к стандартному виду (9.234).
Четвертый
этап – решение СЛАУ МГЭ.
Для решения системы линейных алгебраических
уравнений используются стандартные численные методы. Наиболее распространены
метод неизвестных Гаусса и итерационные методы. Выбор того или иного метода
зависит от конкретных размеров матрицы 
и возможностей
вычислительной техники.
Отметим две важные особенности СЛАУ МГЭ.
Во-первых, матрица является полностью заполненной и несимметричной. В этом
состоит ее существенный недостаток и отличие от глобальной матрицы жесткости
МКЭ, которая является разрешенной (т.е. с большим количеством нулевых
элементов) и симметричной, что позволяет использовать более эффективные
численные методы решения СЛАУ. Вторая особенность матрицы состоит в том, что ее
размер значительно меньше размера матрицы жесткости МКЭ, что существенно
компенсирует отмеченные недостатки. Данная черта матрицы объясняется тем, что в
МГЭ неизвестными являются перемещения и усилия в узлах границы Г, в
то время как МКЭ требует разбиения всей области на конечные элементы.
Следовательно, вектор неизвестных, определяющий размер матрицы СЛАУ, содержит
значения перемещений (или сил) во всех узлах области , число которых много больше граничных узлов.
После решения СЛАУ (9.234) глобальные
векторы перемещений и усилий будут полностью
определены во всех узлах границы Г. Следовательно, зная узловые значения граничных
элементов, можно вычислить перемещения и усилия так же в любой точке границы согласно
интерполяционным соотношениям (9.229).
Пятый
этап – определение граничных напряжений.
В плоской задаче теории упругости основными неизвестными напряжениями являются:
.
Напряжение 
в случае плоского
напряженного состояния равно нулю, в случае плоского деформированного состояния
вычисляется через основные напряжения следующим образом:
.
Напряжения 
и 
равны нулю в обоих вариантах плоской задачи теории упругости.
Согласно граничным условиям
.
Другими словами, два из трех основных напряжений определяются в ходе решения СЛАУ на четвертом этапе.
Для вычисления напряжения 
необходимо воспользоваться законом Гука:
, 
(9.242)
и кинематическими соотношениями, связывающими между собой перемещения и деформации:
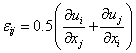, . (9.243)
Так как после решения СЛАУ (9.234) вектор
перемещения оказывается известным, то можно осуществить численное
дифференцирование согласно формуле (9.243) и использовать закон Гука (9.242)
для вычисления .
Шестой
этап – вывод результатов.
Выходная информация
содержит основные сведения о гранично-элементной модели задачи (число
макроэлементов, число граничных элементов, число узлов, число степеней свободы
дискретной системы), тип плоского состояния (плоское напряженное или плоское
деформированное), характеристики глобальной системы линейных алгебраических
уравнений, результаты расчета (глобальные номера узлов и граничных элементов,
значения перемещений, усилий и напряжений в узлах гранично-элементной сетки).
Для вычисления полей перемещений и напряжений во внутренних точках области используется тождество
Сомильяны. Данная процедура не требует решения
системы уравнений, поскольку граничные перемещения уже известны, а тождество Сомильяны осуществляет связь между граничными перемещениями
во внутренних точках области.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
