Главная
9.21.
Метод конечных разностей (МКР)
Этот метод численного решения краевых задач для дифференциальных уравнений называют также методом сеток. Суть метода состоит в следующем. На рассчитываемую область наносится сетка с узлами. Все производные, входящие в дифференциальные уравнения и граничные условия, приближенно заменяются соответствующими разностными отношениями (по формулам численного дифференцирования) и, таким образом, выражаются через неизвестные узловые значения искомой функции. В результате приходим к системе линейных алгебраических уравнений относительно значений функций в узлах сетки. Решение этой системы с последующей интерполяцией в промежутках между узлами позволяет в конечном счете получить приближенное решение рассматриваемой задачи.
Большим преимуществом этого метода является слабая зависимость от граничных условий задачи, геометрии конструкций и характера исходного напряженного состояния. Недостатком является высокий порядок систем алгебраических уравнений. Для МКР также характерны затруднения при учете смешанных граничных условий, рассмотрении многосвязных областей и стыковок областей, описываемых различными дифференциальными уравнениями.
Первые работы по применению МКР к задачам линейной теории упругости были выполнены Г. Маркусом в начале XX столетия. Широкий круг задач был решен Н. П. Абовским, П.М. Варваком, М.А. Колтуновым, М.С. Корнишиным и др. В дальнейшем этот метод применялся для решения плоских задач теории упругости, изгиба пластин, оболочек и т. д.
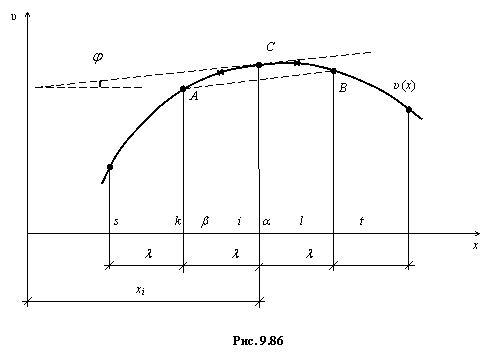
Изложим основные положения МКР на примере одномерной задачи. Пусть, например, υ(x) есть уравнение изогнутой оси балки (рис. 9.86). Точное значение производной в точке С будет равно
Обозначим через 
конечное приращение
аргумента – шаг сетки (разностные отношения будут намного проще,
если 
для всей
рассчитываемой области). Как видно из рис. 9.86, чем меньше шаг 
, тем хорда AB будет ближе к касательной, а угол наклона AB будет приближаться к
углу наклона касательной. Пусть i, k, l, s, t – узлы сетки,
а υi, υk, υl, υs, υt –
узловые значения функции υ(x). Тогда приближенное выражение для производной
в точке i, лежащей посредине интервала [k, l], запишется следующим
образом:
. (9.243)
Приближенное выражение для производной посредине интервала [i, l] можно записать так:
, (9.244)
а посредине интервала [k, i]:
(9.245)
Выражение (9.243) называется центральной разностью в точке i, а (9.244) и (9.245) – соответственно правой и левой разностями в точке i в нецентрированной форме. Все вышеприведенные выражения для первой производной, помимо того, называются первыми разностями.
Вторая производная (вторая разность) в точке i – это первая разность от первых разностей в
точках 
и 
:
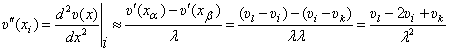. (9.246)
Аналогично вторые разности в точках
l и k:
, 
Третья производная (третья разность) в точке i берется как первая разность от вторых разностей в точках l и k:
.
Четвертая производная (четвертая разность) в точке i – это вторая разность от вторых разностей в точках l, i и k:
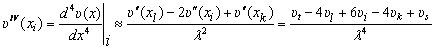. (9.247)
Рассмотрим, как выполняется учет заданных условий по МКР.
Если υi = 0 в точке i, то данное неизвестное просто исключается из системы алгебраических уравнений (соответственно число уравнений в системе уменьшается на одно).
Если υ′ (xi) = 0, то,
подставляя данное условие в (9.243), имеем
, откуда υl
= υk, и одно из этих неизвестных, например υl, также
исключается из системы уравнений.
Если 
, то из выражения второй разности (9.246) можно, например,
выразить υl = 2υi – υk. Данная зависимость также позволяет исключить
одно неизвестное, в данном случае υl.
Пример.
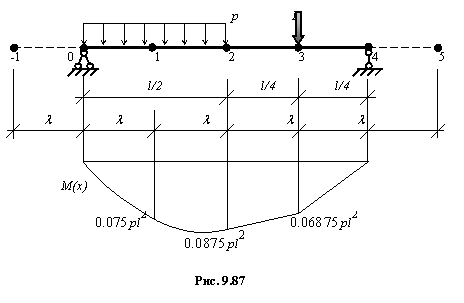
Балка на двух опорах постоянного сечения нагружена распределенной нагрузкой p и сосредоточенной силой F = 0,2pl (рис. 9.87). Необходимо определить прогибы балки.
Решение.
Разделим балку на четыре равные части: 
. Поскольку на
опорах υ0 = υ4 =
0, неизвестными будут узловые значения
прогибов в точках 1, 2, 3.
Примем в качестве математической
модели этой задачи приближенное дифференциальное уравнение изогнутой оси балки:
.
(9.248)
Значения изгибающих моментов,
необходимые в этом случае, приведены на рис. 9.87. Воспользовавшись формулой
вторых разностей (9.246), запишем уравнение (9.248) последовательно для точек 1, 2 и 3:
Подставив
и исключив υ0 и υ4 , получим следующую систему линейных
алгебраических уравнений:
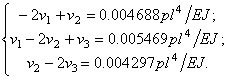
Решив данную систему, имеем:
.
Точные значения прогибов в соответствующих узлах балки:
.
Решим ту же задачу, исходя из дифференциального
уравнения изгиба балки четвертого порядка:
.
(9.249)
В этом случае нет необходимости
предварительно определять значения внутренних изгибающих моментов в узлах
балки. В свою очередь, сосредоточенная
сила F в узле 3 должна быть
представлена в виде распределенной (на интервале) нагрузки: 
, нагрузка же в узлах
1 и 2 соответственно равна: – p, –p/2. Применив формулу четвертых разностей (9.247),
запишем уравнение (9.249) для тех же точек
1, 2 и 3:
;
;
(9.250)
.
Здесь для записи четвертых разностей введены так называемые законтурные узлы -1 и 5, находящиеся вне расчетной области балки. Их можно исключить с помощью граничных условий (на опорах). Так, на левой опоре (узел 0):
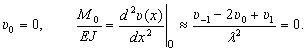
Отсюда υ-1 = – υ1. Такие же условия на правой опоре (узел 4), поэтому υ5 = –υ3.
Подставив в (9.250) 
и исключив
неизвестные: υ0 = υ4 =
0, υ-1 = –υ1 и υ5 = –υ3, получим систему алгебраических уравнений:
;
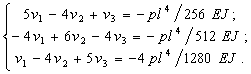Решением данной системы будут следующие значения прогибов в узлах балки:
что совпадает с результатами предыдущего расчета (использующего в качестве математической модели уравнение (9.248)).
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
