Главная
9.22. Вариационно-разностный
метод (ВРМ)
ВРМ лишен
большинства перечисленных для МКР недостатков, поскольку основан на
вариационных принципах механики.
Поведение деформируемых систем в этом случае описывается условием
стационарности некоторого функционала, являющегося обычно выражением
потенциальной (функционал Лагранжа) или дополнительной (функционал Кастилиано)
энергии системы. Это условие стационарности эквивалентно
основным дифференциальным уравнениям данной задачи, но при этом дает
возможность понизить порядок производных, входящих в вариационное уравнение,
упрощает формулировку граничных условий (например, при использовании
функционала Лагранжа статические граничные условия не рассматриваются
специально, а входят в вариационное уравнение и называются естественными), а также
позволяет удобно алгоритмизировать все этапы расчета конструкции.
Идея ВРМ
состоит в замене вариационной задачи ее дискретным аналогом в сеточной области
– т. е. искомая непрерывная функция, входящая в выражение полной потенциальной
энергии системы, определяется дискретно, на некотором множестве узлов. При формировании системы алгебраических
уравнений исходный функционал
энергии, записанный для всей области, заменяется некоторой конечной суммой, а
входящие в него производные – конечными разностями. Матрица коэффициентов системы разрешающих
уравнений ВРМ получается симметричной, хорошо обусловленной и имеет ленточную
структуру.
ВРМ получил
свое развитие благодаря первой работе в этом направлении В. Вазова и Дж.
Форсайта и последующим работам Н. П. Абовского, Д. В.
Вайнберга, Л. В. Енджиевского,
А. С. Сахарова, А. Л. Синявского и других авторов. В этих исследованиях был рассмотрен широкий
класс задач теории упругости, а также теории пластин и оболочек со сложным
характером граничных условий.
Обозначим
через U – потенциальную энергию деформации системы
(в случае изгиба балки – это энергия внутреннего изгибающего момента 
), а через W – возможную работу
внешних сил, которые считаются при этом неизменными как по величине, так и
по направлению. Выражение П=U–W называется полной потенциальной
энергией системы. Сформулируем вариационный принцип Лагранжа: среди
всех геометрически возможных перемещений (т. е. удовлетворяющих условиям сплошности и заданным граничным условиям) в действительности имеют место только те
перемещения, которые придают потенциальной энергии системы П стационарное
значение (в случае устойчивого равновесия потенциальная энергия системы имеет
минимальное значение).
Выражение для
полной потенциальной энергии (функционал Лагранжа) представляет собой
квадратичную функцию от узловых значений перемещений (прогибов υi), и
условие минимума этой энергии может быть записано в виде
или 
,
где i пробегает
все номера узлов, принадлежащих балке при выбранном шаге разбиения. Причем
ненулевые значения производная принимает лишь в узлах, для которых
соответствующие выражения в конечных разностях содержат υi.
Поясним эти
рассуждения на примере задачи изгиба балки, находящейся под действием
распределенной нагрузки p (рис. 9.88, а). Пусть шаги деления
одинаковы и равны 
, а количество узлов –
n.
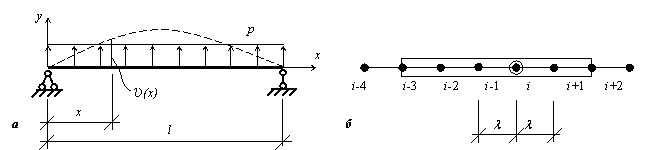
Рис.9.88
Функционал Лагранжа в этом случае запишется так:
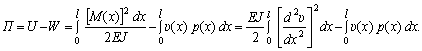(9.251)
При дискретизации
интегралы приближенно заменяются суммированием по всем узлам, а вместо
производных подставляются разностные отношения. Тогда выражение (9.251) примет
следующий вид:
(9.252)
Перепишем
выражение (9.252) в развернутом виде
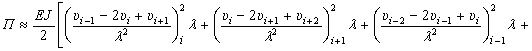
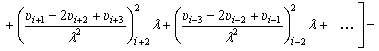(9.253)
.
Здесь нижний
индекс у круглых скобок указывает, к каким узлам относятся производные, т. е. какие это части потенциальной
энергии.
Условие минимума полной потенциальной энергии:
(9.254)
При этом
уравнение (9.253) сокращено на и учтено правило
дифференцирования для вычисления полных дифференциалов:
где под 
подразумеваем скобку,
содержащую выражения производных в конечных разностях. Таким образом, при минимизации по υi остались лишь скобки, содержащие υi (для узла
i и прилегающих i–1,
i+1).
Перепишем
выражение (9.254) в следующем виде:
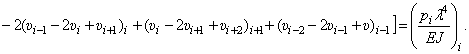(9.255)
Уравнением (9.255)
будет удобно пользоваться, если ввести так называемые весовые
функции 
, зависящие от
положения узла в расчетной области. Так,
если узел находится внутри области – = 1, на границе –= 0,5, вне области –= 0. Например, для узлов, приведенных на рис. 9.88, б, 
, 
, 
. В результате (9.255)
можно записать в виде
(9.256)
В частном
случае, когда 
, уравнение (9.256) примет вид, эквивалентный выражению для
четвертой разности (9.247).
Пример.
Проиллюстрируем алгоритм ВРМ на примере расчета двухопорной балки (см. рис. 9.89).
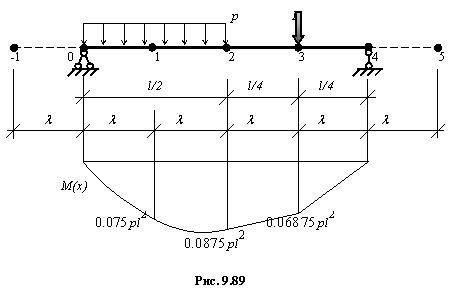
Решение.
Запишем
условие минимума полной потенциальной энергии балки, используя для этого
выражение (9.256), где i
последовательно принимает значения узлов с неизвестными перемещениями,
т. е. 1, 2, 3:
Подставим в
полученные уравнения значения нагрузки p (p1 = –p, p2 = – p/2, p3 = – 4p/5) и весовых функций (
):
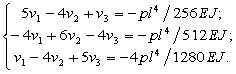
Подставив 
и исключив
неизвестные υ0
= υ4 = 0,
υ-1 = –υ1 , υ5 = –υ3, получим следующую систему уравнений:
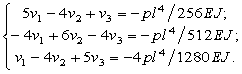
Результатом
будут такие же значения прогибов, что и при решении задачи МКР:
В заключение
данного параграфа укажем на еще один приближенный метод, в основе которого
лежит вариационный принцип Лагранжа.
Метод Ритца позволяет получить, в
отличие от большинства других методов, не числовое, а аналитическое
приближенное решение вариационной задачи. Аппроксимация искомого решения здесь
производится по всей расчетной области с помощью линейной комбинации
независимых функций с произвольными (неизвестными) коэффициентами. Например,
для задачи изгиба балки функцию прогиба можно представить в виде
, (9.257)
где 
– неизвестные постоянные множители, подлежащие определению; 
– последовательность аппроксимирующих
(базисных) функций, которые должны
удовлетворять условиям линейной независимости и полноты, а также кинематическим
граничным условиям (на опорах). Число
членов n в сумме может быть различным, в зависимости от необходимой
точности получаемого решения.
Если
подставить аппроксимацию (9.257) в функционал полной потенциальной энергии
системы (9.251), получим функцию n переменных
Условие минимума
этой функции
(9.258)
Выражение (9.258)
является системой линейных алгебраических уравнений относительно (система уравнений
Ритца). Решив систему и подставив
найденные значения в (9.257), получим приближенное решение вариационной
задачи (9.251) по Ритцу:
.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
