Главная

Теоретическое обоснование механизма упрочнения цементного камня введением тонкодисперсных минеральных наполнителей

1. Влияние пористости на прочность цементного камня

Наряду со структурно-механической неоднородностью кристаллогидратной связки важнейшим структурным фактором, оказывающим влияние на прочность и другие физико-механические свойства цементного камня и бетонов на цементных вяжущих, является пористость. Расход цемента, водоцементное отношение, интенсивность уплотнения бетонной смеси, условия и длительность твердения являются теми технологическими параметрами, которые определяют пористость и соответственно прочность цементного камня и бетона.

Современные представления о структуре порового пространства цементного камня были заложены в конце 40-х гг. Т.Пауэрсом, Т.Брауньярдом и позднее усовершенствованы на основе обширных экспериментальных исследований П.П.Ступаченко [6], Ю.В.Чеховским [7,8], В.С. Данюшевским [3,4] и др.

Как показывает структурный анализ с использованием сорбционных методов, ртутной и оптической порометрии, поровое пространство цементного камня, характеризующееся общей (интегральной) пористостью П, является многоранговым и включает поры нескольких характерных размеров. На кривых дифференциальной пористости цементного камня, твердевшего в нормальных условиях или в условиях тепловлажностной обработки при нормальном давлении, фиксируются три характерных пика, соответствующих так называемым гелевым (средний радиус около 2 нм), "промежуточным" (40 нм) и капиллярным (300...2000 нм) порам (рис.1.) [5]. Цементный камень содержит также 2...4% макропор со средним размером 0,1 см и более в виде защемленного (вовлеченного) воздуха [9]. Каждая из этих четырех групп пор имеет определенную физическую природу, чем и обусловливается концентрация каждого типа пор на дифференциальной кривой распределения около своего среднего размера. В частности, гелевые поры соответствуют промежуткам между частицами гидросиликатной составляющей кристаллогидратной связки, "промежуточные" поры - интервалам между частицами крупнокристаллических продуктов гидратации, и капиллярные - части объема цементного камня, не заполненной поризованными продуктами гидратации.

В.С.Данюшевским и К.А.Джабаровым на большом экспериментальном материале установлены границы размеров каждого вида пор в портландцементном камне [5]. В частности, граница гелевых и "промежуточных" пор соответствует радиусу 10 нм, "промежуточных" и капиллярных 50 нм (см.рис.1.). Граница всех внутрикристаллогидратных и капиллярных пор и граница объема кристаллогидратного сростка и капиллярного пространства соответствует, таким образом, радиусу пор »50 нм.

Рис.1. Дифференциальные кривые распределения пор по радиусам в цементном камне:

- - - - - по изотермам десорбции; ^_____ методом ртутной порометрии.

В современной механике используется несколько видов зависимостей для описания связи прочности и пористости R=f(П). Наиболее полная систематизация сведений по этому вопросу содержится в монографии Р.Райса [11]. В частности, широкое распространение получила степенная зависимость М.Ю.Бальшина [1]

где R₀- прочность плотной (непоризованной) фазы; s - степенной показатель, отражающий интенсивный (s>1) характер нарастания прочности R со снижением пористости или с ростом относительной объемной концентрации твердой фазы (относительной плотности) V=1-П. По экспериментальным данным для реальных материалов значение показателя s колеблется в пределах от 3 до 6, при этом меньшее значение s соответствует относительно однородным структурам, а большее наиболее неоднородным.

Помимо этого используется формула Е.Рышкевича, описывающая связь прочности и пористости в экспоненциальной форме [12]

здесь b - константа.

Третий часто используемый вид зависимости, предложенный К.Шиллером [13], имеет вид

где П_cr - так называемая критическая пористость, соответствующая нулевой прочности.

Формула (3) позволяет учесть то естественное обстоятельство, что начало роста прочности предполагает некоторую начальную (критическую) объемную концентрацию твердой фазы V_cr, то есть выполняется условие R=0 при П > П_cr=1-V_cr.

Зависимости (1-3) отражают реально наблюдаемый экстенсивный характер снижения прочности при увеличении пористости, что обусловлено тем, что при повышении пористости наибольшие напряжения на контуре пор возрастают быстрее, чем снижается рабочая площадь сечения.

Привязка формул, подобных (1-3), к конкретным условиям достигается обычно подбором констант уравнений s, b, П_cr (V_cr) при обработке экспериментальных данных, при этом диапазон констант для разных материалов оказывается достаточно широким. Можно констатировать таким образом, неоднозначность связи R/R₀=f(П), проявляющейся в том, что при одинаковой общей (интегральной) пористости или одинаковой относительной объемной концентрации твердой фазы V относительная прочность материалов R/R₀ различается до нескольких раз. Эти различия прочности связывают обычно с различием уровней структурной неоднородности пористых материалов, не указывая конкретно на структурные факторы, обусловливающие эту неоднородность.

Естественно, что указанные различия определяются различиями реакции структуры на приложение нагрузки и обусловлены влиянием конкретных параметров структуры, и в частности, структуры порового пространства. Помимо общей пористости, таким образом, существуют другие структурные факторы, которые оказывают самостоятельное влияние на механизм разрушения и прочность.

Такими факторами являются, в частности, разноразмерность пор (многоранговость пористости) и неупорядоченности их распределения в объеме, характеризующие дифференциальную пористость; геометрическая конфигурация пор, наличие или отсутствие в твердой непоризованной фазе начальных остроконечных дефектов типа трещин, соотношение размера пор по отношению к размеру начальных дефектов и объемное насыщение таких дефектов.

Рассмотрим задачу о влиянии неупорядоченности распределения пор в объеме в виде разброса локальных значений пористости p (или локальной относительной плотности v=1-p). Примем в качестве модели пористой структуры геометрически однородную пористую систему, состоящую из однотипных и одноразмерных (v=V=const) объемных (трехмерных) структурных ячеек пор одинакового размера. Под структурной ячейкой будем иметь ввиду микрообъем пористого материала, включающий фрагмент (мостик) твердой фазы и окружающие его поры.

В условиях однородного растяжения все структурные ячейки рассматриваемой системы будут нагружены одинаково и ее разрушение можно рассматривать как одновременное разрушение всех ячеек, при этом по аналогии с (1) прочность такой системы можно представить как

где n - степенной показатель, отражающий изменение коэффициента концентрации напряжений с изменением v для однородной структуры. Очевидно, значение n будет меньше показателя s, соответствующего реальному неоднородному материалу (1).

Усложним теперь пористую систему, допустив флюктуации относительных плотностей твердой фазы структурных ячеек v. Такую систему можно получить, например, из системы с равноплотными ячейками v=const, трансформировав их в ячейки такого же типа, но имеющие разные значения v, и при этом сохранив общее количество ячеек. Очевидно, что обе эти системы будут иметь одинаковую интегральную относительную плотность V.

Для такой неоднородной системы поверхность разрушения будет представлять собой набор разноплотных структурных ячеек, распределенных по некоторой функции j(v). В условиях равномерного растяжения мостики твердой фазы ячеек в сечении окажутся загруженными неодинаково. Наиболее нагруженными по величине пикового напряжения на контуре поры окажутся ячейки с наименьшей v₀, а наименее нагруженными - с наибольшей относительной плотностью v_m.

Можно ожидать, что неоднородность распределения напряжений, являющаяся следствием структурной неоднородности, обусловит ступенчатый характер разрушения пористого материала. В общем случае приложение некоторой внешней нагрузки приведет к разрушению части наиболее перегруженных структурных ячеек общей площадью , при этом доля нагрузки, которую несла в сечении разрушившаяся часть ячеек, перераспределится между сохранившимися более плотными ячейками общей площадью

Если после такого перераспределения напряжение в наиболее нагруженной точке самой перегруженной из сохранившихся ячеек будет меньше или равным R₀, то процесс разрушения приостановится. В этом состоянии равновесия наибольшая возможная нагрузка на единицу площади материала (напряжение) составит

Последующее возрастание внешней нагрузки, приводящее к локальным разрушениям отдельных микрообъемов без разрушения всего образца, возможно лишь до определенной стадии нагружения. При некоторой нагрузке, являющейся критической, локализация разрушения становится невозможной и процесс перерастает в лавинное разрушение с последовательным выходом из строя всех структурных ячеек. Этот критический уровень нагрузки и соответствует прочности хрупкого пористого материала, величину которой можно получить как экстремальное значение σ по v.

Рассмотрим некоторые частные случаи функции распределения φ(v).

1. Случай равномерного распределения структурных ячеек по локальным плотностям (рис.2, функция 2),

В этом случае уравнение промежуточного состояния системы (5) будет иметь вид

Из условия находим и формулу прочности

Полученная формула справедлива при . Спецификой механизма разрушения материала в данном случае будет локальное предварительное разрушение в отдельных микрообъемах, предшествующее полному разрушению. При невыполнении этого условия механизм разрушения качественно меняется: в данном случае разрушение самой "слабой" группы ячеек и последующее перераспределение нагрузки вызовет последовательное разрушение всех остальных ячеек без увеличения внешней нагрузки, т.е. прочность структуры будет определяться прочностью самой "слабой" ячейки

При оценке прочности в этом случае будет справедлива гипотеза "слабого звена".

2. Случай линейной функции распределения φ(v) с максимумом в области v₀ (рис.2, функция 3).

Для рассматриваемого случая анализ промежуточного состояния системы на экстремум по v дает формулу прочности в следующем виде:

Формула справедлива при . При невыполнении этого условия прочность определяется формулой (8).

Аналогично определяется формула прочности для линейной функции распределения φ(v) с максимумом в области v_m (рис.2, функция 4).

Рис.2. Зависимость относительной прочности R/R₀ от интегральной относительной плотности V пористой одноранговой (m=1) структуры

для равномерной и линейных функций распределения 𝜑(V) локальных относительных плоскостей:

^_______ - механизм разрушения в соответствии с гипотезой «слабого звена»;

--------- - механизм разрушения с локальным предразрушением материала;

цифры на кривых (1,2,3,4) соответствуют функциям распределения φ(V).

3. Случай функции нормального распределения φ(v) (рис.3, функция 2).

Уравнение промежуточного состояния системы будет иметь вид

где V- интегральная плотность твердой фазы, равная математическому ожиданию; - среднеквадратичное отклонение.

Из условия находим v_cr и формулу прочности

где - функция Лапласа (табулирована).

4. Случай функции нормального распределения структурных ячеек по локальным плотностям с коэффициентом асcимметрии А≠0 и эксцесса Е≠0 (рис.3, функция 4).

Данный случай реализуется путем представления функции плотности в виде ряда Грама-Шарлье.

где , , - функция плотности нормированного и центрированного нормального распределения и ее производные.

Анализ промежуточного состояния на экстремум по v дает формулу прочности в виде

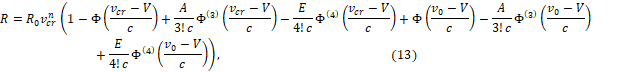
где , - производные функции Лапласа (табулированы).

Предельные значения коэффициентов ассиметрии А и эксцесcа Е находятся из условия φ¢(v)=0

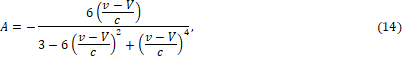
Рис.3 Зависимость относительной прочности R/R₀ от интегральной относительной плотности V пористой одноранговой (m=1) структуры

для нормальной функции распределения φ(V) локальных относительных плоскостей и ассиметричного распределения:

^_______ - механизм разрушения с локальным предразрушением материала;

цифры на кривых (1,2,3) соответствуют функциям распределения φ(V).

Численное значение показателя n в формуле (5) должно находиться, по-видимому, в диапазоне 1...3. Меньшее значение этого диапазона n=1 будет соответствовать идеальной однородной структуре, состоящей из одинаковых структурных ячеек, мостики твердой фазы которых нагружены равномерно (без проявления концентрации напряжений). Большее значение n=3 равно наименьшему значению показателя s в формуле М.Ю.Бальшина (1) и соответствует наиболее однородным реальным материалам.

Зависимости относительной прочности R/R₀ пористого материала от V с учетом специфики механизма разрушения для нескольких значений n, соответствующих указанному выше диапазону (n=1,5; 2; 3), для одноранговой (m=1) пористой структуры для нескольких функций распределения локальных плотностей приведены на рис.2 и 3. На рис.3 кривая 3 описывает совокупность точек по сочетаниям А и Е, соответствующих минимальным значениям R. Все другие сочетания количественных значений асимметрии и эксцесса лежат в пределах площади, ограниченной кривыми 3 и 1.

Анализируя рис.2 и 3 можно сделать вывод, что степень влияния неоднородности пористости на прочность пористых материалов с хрупкой структурообразующей фазой в области малых значений интегральной плотности V=0,1...0,3 достигает десятичного порядка, в области средних значений V=0,3...0,7 составляет до 2...5. В области высоких значений V (низкой пористости) влияние структурной неоднородности на прочность оказывается минимальным.

С целью оценки роли многоранговости пористости рассмотрим пористую систему, состоящую из однотипных пор двух существенно отличающихся размеров d₂>>d₁ (d₂/d₁>>1). При этом учтем представления Д.Хассельмана, Р. Фулрата и Р.Бертолотти [14,15] о влиянии размера пор на прочность реального материала.

Твердая непоризованная фаза реального материала обладает дефектной структурой с некоторой объемной концентрацией дефектов типа гриффитсовских микротрещин с характерным размером l. Согласно [14,15] характер снижения прочности пористого материала с повышением концентрации пор некоторого размера d существенно зависит от соотношения d/l. Принципиальный характер влияния пористости на прочность и экспериментальные данные Д.Хассельмана [15] по прочности на растяжение при изгибе поризованного боросиликатного стекла, иллюстрирующие влияние размера пор, приведены соответственно на рис.4 и 5. В случае 1, когда размер пор значительно меньше размера микродефектов d/l << 1, область концентрации напряжений около поры мала и до определенного уровня пористости поры практически не взаимодействуют с микродефектами (см. рис. 4). В этом случае одиночная пора по уровню концентрации напряжений не является более "тяжелым" дефектом, чем уже имеющиеся в объеме микродефекты, и относительная прочность материалов R/R₀ весьма медленно понижается с понижением V.

В случае 3, когда размер пор значительно больше размера микродефектов d/l >> 1, область концентрации напряжений около поры достаточно велика, так что микродефекты активно насыщают эту область (см.рис.4). В этом случае для хрупкой твердой фазы появление уже нескольких первых пор обусловит сброс прочности, количественно примерно обратно пропорциональный коэффициенту концентрации напряжений k для одиночной поры, с последующим монотонным понижением прочности при снижении V. При описании зависимости прочности одноранговой структуры R₁ от V в случае d/l>>1 за исходную прочность R, соответствующую V=1, следует принимать прочность плотной фазы R₀, уменьшенную в k раз, с учетом того, что от этого уровня прочности наблюдается ее монотонное понижение

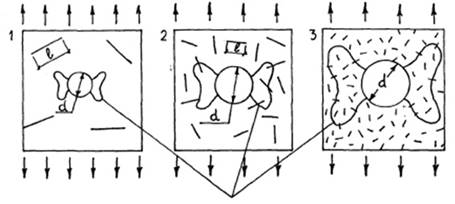
Области концентрации напряжений в условиях осевого растяжения

Рис. 4. Три случая взаимодействия начальных дефектов твердой фазы и пор:

1 – случай d/1<<1; 2 – случай d/1≈1; 3 – случай d/1>>1.

Случай 2 - промежуточный, и он соответствует d/l≈1. С повышением пористости снижение прочности в данном случае определяется умеренным взаимодействием начальных дефектов с порами с появлением первых пор, что отражено определенным сбросом прочности при П≈0.

В экспериментах на рис.5 диапазон изменения диаметров пор (d=5...180 мкм) был выбран таким, чтобы охватить описанные случаи.

Рис. 5. Относительная прочность R/R₀ поризованного боросиликатного стекла на растяжение при изгибе

в зависимости от относительной объемной концентрации твердой фазы V и диаметра пор:

диаметр пор, мм.:

○ – 5…10; - 10…20; ● – 20…36; - 36…74; - 74…105; □ – 105…186.

Заменяя комбинацию "дефект-пора" комбинацией "две группы разноразмерных пор", используем специфику взаимодействия разнородных и разноразмерных дефектов для оценки прочности двухранговой хрупкой пористой структуры. Такую структуру можно получить путем поризации одноранговой структуры порами размера d₂. Тогда интегральная относительная плотность двухранговой структуры будет равна

где V₁ - относительная плотность исходной одноранговой структуры, имеющей прочность R₁; П₂ - часть пористости, соответствующая порам размера d₂.

Если допустить, что d₂>>d₁ и что, на основании этого, объем материала, соответствующий области концентрации напряжений около поры диаметром d₂ по прочности адекватен одноранговой пористой структуре, то двухранговую структуру можно представить как некоторую непрерывную фазу с прочностью R₁, поризованную системой пор d₂. Допуская далее, что форма пор d₂ и их распределение в объеме подобны этим характеристикам одноранговой пористой структуры, то на основании формулы М.Ю.Бальшина (1), а также учитывая (16) и (17), будем иметь для прочности двухранговой структуры при d₁/l>>1

где V₂=1-П₂.

Распространяя эти рассуждения на многоранговые структуры с хорошо выраженным разрывом размера пор смежных рангов (d₁<<d₂<<...<<d_m), получаем следующую формулу прочности m-ранговой пористой структуры

Из (19) можно видеть, что повышение прочности пористого материала, возможно, таким образом, не только снижением общей пористости, но и путем снижения числа рангов пор (выравниванием размера пор).

Механизм разрушения цементного камня при сжатии определяется взаимодействием пор нескольких рангов: гелевых, "промежуточных", капиллярных и макропор.

При объемной концентрации вовлеченного (защемленного) воздуха в цементном камне 2...5% макропоры этой природы с размером (диаметром) 0,005...0,5 см (50... 5000 мкм) и более представляют одиночные невзаимодействующие между собой макродефекты, отстоящие друг относительно друга на расстоянии нескольких диаметров (рис. 6а).

Рис.6 Структура цементного камня в поле оптического микроскопа (а) и макроструктурная ячейка,

включающая одиночную макропору защемленного воздуха и капиллярные поры (б):

1 – одиночная макропора; 2 – микропоры.

Ниже на примере двухранговой пористой структуры с хрупким типом структурообразующей фазы, поризованной малыми порами (микропорами) и включающей одиночные невзаимодействующие макропоры, рассматриваются теоретические аспекты разрушения материалов со сложной пористой структурой при сжатии. Применительно к цементному камню микропоры в данном случае соответствуют капиллярным порам, макропоры - вовлеченному (защемленному) воздуху. Поведение материала с подобной структурой при нагружении будет определять макроструктурная ячейка, включающая одиночную макропору и прилегающую к этой макропоре поризованную микропорами структурообразующую фазу (рис.6б).

Характер напряженного состояния в окрестности одиночной поры сферической конфигурации в условиях равномерного сжатия интенсивностью σ₀ определяется данными теории упругости [2,10] (рис.7а). В полярной области сферической полости имеет место всестороннее растяжение с наибольшим растягивающим напряжением σ_b в точке B на контуре поры (здесь и далее для растягивающих напряжений принят знак минус)

где k₁- коэффициент концентрации растягивающих напряжений в точке В на контуре поры; μ - коэффициент Пуассона материала.

В экваториальной области сферы имеет место концентрация сжимающих напряжений при наибольшем значении напряжения на контуре поры в точке A

где k₂- коэффициент концентрации сжимающих напряжений в точке A.

На рис.7б в координатах k₁, k₂ = f(m) приведена графическая интерпретация зависимостей (20) и (21) для m=0,1...0,4, показывающая, что наибольшее напряжение сжатия σ_a мало зависит от коэффициента Пуассона, при этом k₂ = s_a/s₀ ≈ 2, а s_b зависит от 𝜇 существенно. Для диапазона m=0,1...0,3 соотношение k₁ = s_b/s₀ изменяется в пределах 0,33...0,63. Напряженное состояние на рис.7а соответствует случаю m=0,3.

Рис.7. Напряженное состояние в окрестности одиночной сферической поры в условиях равномерного сжатия (а)

и зависимости коэффициентов концентрации напряжений в точках А и В на контуре поры от коэффициента Пуассона (б).

Согласно принципу Сен-Венана и в соответствии с рис.7а локальное возмущение напряжений в окрестности сферической полости распространяется на расстояние порядка одного диаметра от границы полости, а интенсивный характер этого возмущения наблюдается в пределах 1/4 диаметра. Применительно к цементному камню для макропоры вовлеченного воздуха диаметром d₂=0,1 см в области высокой концентрации напряжений на линейном отрезке 0,1/4=0,025 см (250 мкм) разместится приблизительно 10²...10³ капиллярных пор диаметром d₁=0,1...1 мкм. Таким образом, взаимодействие капиллярных пор цементного камня с областью концентрации напряжений около макропор вовлеченного воздуха соответствует случаю высокой объемной концентрации микродефектов в названной области (d₂/d₁ >> 1), что с учетом хрупкого типа структурообразующей фазы (кристаллогидратного сростка) позволяет учесть влияние этого взаимодействия на прочность при сжатии постоянным коэффициентом концентрации напряжений в формуле (19) равным k = k₂ ≈ 2.

Приняв пористую структуру цементного камня трехранговой (m=3) и k=2 (поры сферической конфигурации) на основании (19) можно показать, что многоранговость пористой структуры снижает прочность на сжатие в 8 раз.

Как указывалось выше, прочность на сжатие цементной пасты определяется взаимодействием пор нескольких рангов. В ходе гидратации цемента в пространстве между гранулами клинкера формируется поризованная кристаллогидратная связка, постепенно заполняющая межзерновое пространство, что обусловливает одновременное снижение объема и размера капиллярных пор при сравнительно небольшом изменении размеров внутрикристаллогидратных пор. Процесс таким образом протекает с постепенным понижением соотношения и сближением размеров капиллярных и внутрикристаллогидратных пор, что при прочих равных условиях способствует снижению многоранговости пористости. Объем и размер макропор защемленного воздуха в процессе твердения остаются практически постоянными.

Таким образом, снижение многоранговости пористости возможно путем регулирования капиллярной пористости через понижение среднего размера пор этого ранга.

Объемную концентрацию твердой фазы в исходной водовяжущей пасте V_x0 можно представить через водоцементное отношение w и соотношение плотностей воды и вяжущего g в следующем виде:

а обьем поризованной кристаллогидратной массы V_y, включающий объем непрогидратированного вяжущего, для некоторой промежуточной стадии степени гидратации q:

где ϑ - коэффициент увеличения объема твердой фазы при химическом переходе вяжущего в гидрат (в этот объем включена внутрикристаллогидратная пористость). Согласно авторам [16] ϑ_max=2,2.

Тогда средний размер капиллярной поры d, трактуемый как среднее расстояние между флокулами гидратируемых частиц вяжущего, может быть представлен как отношение капиллярной пористости 1-V_y к удельной поверхности развивающихся флокул S_y, скорректированное нормирующим коэффициентом n:

где n = 5...7, S_x0- удельная поверхность исходного вяжущего (см²/г), γ_x - плотность вяжущего (г/см³).

Более строгаязависимость для определения d должна учитывать потери S_y из-за ее поглощения формирующимися межфлокулярными константами.

На рис.8 представлена графическая интерпретация зависимости (24) в координатах "средний размер капиллярных пор d - степень гидратации θ, иллюстрирующая снижение среднего размера капиллярных пор со снижением водоцементного отношения.

Рис.8. Зависимость среднего размера капиллярных пор d цементного камня от степени гидратации θ:

1,2,3,4 – водоцементное отношение w=0,2; 0,4; 0,5; 0,6 соответственно.

2. Модифицирование дифференциальной пористости цементного камня введением тонкодисперсных минеральных наполнителей

Основные факторы позитивного влияния тонкодисперсных минеральных наполнителей на прочность цементного камня так или иначе связаны с его пористой структурой.

В разделе 1 показана зависимость прочности цементного камня от среднего размера капиллярных пор и неоднородности распределения локальных значений пористости в объеме, характеризующих дифференциальную пористость. При этом уменьшение среднего размера данных пор с повышением степени гидратации "чистого" цементного камня происходит только за счет увеличения объема кристаллогидратной фазы при химическом переходе вяжущего в гидрат. Исходная пустотность в дифференциальной форме по размеру пустот p для такой водовяжущей системы (ячейка 1 на рис.9) будет соответствовать зависимости dV/dp на рис.9а при некотором среднем размере пустот p₁. В процессе гидратации крупные в исходном состоянии пустоты очень медленно и слабо перекрываются гидратной связкой, оставаясь крупноразмерными капиллярными порами, что для такой водовяжущей системы определяет ярко выраженную многоранговость формирующейся структуры цементного камня с большим значением среднего размера капиллярных пор d₁ (рис.9б).

Рассматривая возможность введения тонкодисперсных наполнителей, удельная поверхность которых выше удельной поверхности портландцемента мы исходим из предпосылки, что когда гранулы наполнителя размещаются между частицами вяжущего, то при этом существенно изменяется исходная дифференциальная пустотность водовяжущей пасты.

Сущность этого изменения заключается в том, что мелкие гранулы наполнителя перекрывают значительную часть обьема исходных крупных пустот, что меняет дифференциальную пустотность системы в благоприятном направлении, уменьшая средний размер пустот на дифференциальной зависимости p₂ < p₁ (рис.9в). В процессе твердения в данном случае развивается структура с формированием благоприятной для прочности дифференциальной пористости цементного камня при быстро понижающемся взаимодействии рангов пор в силу быстрого снижения размера крупных капиллярных пор d₂ < d₁ (рис.9г).

Рис.9. Дифференциальная пустотность паст без наполнителя (а) и с добавкой тонкодисперсного наполнителя (в)

и соответствующая им дифференциальная пористость цементного камня (б, г).

Принципиальный характер влияния микронаполнителя на капиллярную пористость цементного камня можно показать на примере простейшей регулярной плоской модели водовяжущей системы, состоящей из одноразмерных частиц вяжущего диаметром a_x0 единичной толщины, распределенных по квадратной сетке с шагом b (рис.10а). Для рассматриваемой модели водоцементное отношение можно представить следующим образом

По ходу твердения происходит растворение и гидратация частиц вяжущего, при этом для промежуточной стадии твердения, соответствующей степени гидратации θ, размеры частицы вяжущего a_x и гидратирующей флокулы a_y в предположении увеличения ее размера по механизму концентрического развития частицы исходного вяжущего составят

При этом наибольшее относительное расстояние между частицами d_max в функции от θ, соответствующее наибольшей условной капиллярной поре в модельной ячейке (см. рис.10а), составит

Введение в водовяжущую систему размещаемых в центре ячеек гранул инертного наполнителя с размером a_f обусловит формирование при твердении условных капиллярных пор d_max1, d_max2, меньших по размеру относительно наибольшей поры d_max в твердеющей системе без наполнителя (см. рис.10б). Количественный анализ дал следующие зависимости для относительного размера d_max1/d_max в функции от степени гидратации (случай одинаковых плотностей вяжущего и наполнителя):

- для постоянного водоцементного отношения w=const

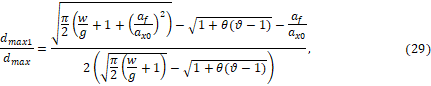
- для постоянного водотвердого отношения w¢=const

Подобные соотношения применительно к рассматриваемой модели получены и для размера d_max2/d_max (см.рис. 10б).

Данные по расчету относительных размеров d_max1/d_max и d_max2/d_max для случая a_f/a_x0=0,3, что соответствует объемной концентрации наполнителя около 1/10 от вяжущего, при v=2,2 для нескольких значений w и w¢ представлены на рис.10в,г. Эти данные показывают, что при введении наполнителя уже на стадии затворения происходит значительное уменьшение размеров исходных пустот при быстром снижении относительных размеров капиллярных пор по ходу гидратации.

Рис.10. Зависимость относительных размеров капиллярных пор от степени гидратации ячейки водовяжущей пасты

с гранулой наполнителя по отношению к ячейки пасты без наполнителя для случая :

1,2,3 (4,5,6) - для w = 0,3; 0,4 и 0,6 соответственно;

– то же, для = 0,3; 0,4 и 0,6 соответственно.

В обзоре показано, что введение тонкодисперсных наполнителей возможно двумя принципиально различными способами. Согласно первому варианту микронаполнитель вводится в водовяжущую систему без изменения содержания цемента, взамен части песка в бетоне. Второй вариант предполагает введение наполнителя путем замены части цемента равным объемом наполнителя.

Рассмотрим первый вариант. Для бинарной дисперсной системы включающей, наряду с вяжущим (x), некоторое количество наполнителя (f) по обьему вяжущего V_f = αV_x0, плотности g_f=zg_x, а также при дисперсности наполнителя по удельной поверхности S_f = bS_x0 и гидравлической активности q_f = xq_x общая удельная поверхность всех гидратирующихся флокул определится как

Раскрывая это выражение получим

Сумма объемов поризованной кристаллогидратной массы, непрогидратировавшего вяжущего и наполнителя будет

Учитывая принятые допущения получим

Тогда средний размер капиллярной поры, по аналогии с (12) с учетом (10) определится как

Графическая интерпретация данной зависимости для S_x0=3000 см²/г, g_x=3,15 г/см³ представлена на рис.11.

Анализируя (12) и (35), можно видеть, что средний размер капиллярных пор d в цементном камне на бинарном вяжущем при прочих равных условиях будет существенно снижаться с повышением дисперсности (увеличением b) и концентрации (a) наполнителя, а также при снижении водоцементного отношения (w) по сравнению со структурой на исходном немодифицированном вяжущем (см. рис.11а,б,в) При этом на размер капиллярных пор оказывает влияние также гидравлическая активность (изменение ξ) и плотность (изменение z) наполнителя d (рис. 11в,г).

Рис.11. Зависимость среднего размера капиллярных пор d от степени гидратации θ_x для цементных систем с введением тонкодисперсного наполнителя

без изменения содержания цемента при изменении водоцементного отношения (а),

дисперсности (б), объемной концентрации (в), пуццоланической активности (г) и плотности (д) наполнителя:

1,2 – система без наполнителя при w=0,3; 0,2 соответственно;

3,4 – система с тонкодисперсным наполнителем при α=0,3; β=5; z=1; ξ=0; w=0,3; 0,2 соответственно;

5,6,7 – тоже при α=0,3; z=1; ξ=0; w=0,3; β=1;5;10 соответственно;

8,9,10 – тоже при β=5; z=1; ξ=0; w=0,3; α=0,1; 0,2; 0,3 соответственно.

Рис.11. (продолжение):

11, 12, 13 – система с тонкодисперсным наполнителем при α=0,3; β=5; z=1; w=0,3; ξ=0; 0,5; 1 соответственно;

14, 15, 16 – тоже при α=0,3; β=5; z=1; w=0,3; ξ=0; z(γ_f)=0,32 (1 г/см³); 0,82 (2,6 г/см³); 1,27 (4 г/см³) соответственно.

Определим средний размер капиллярной поры для второго варианта введения наполнителя путем замены части вяжущего равным объемом наполнителя. Общая удельная поверхность всех флокул S_yобщ будет определяться как

Раскрывая это выражение получим

Сумма объемов поризованной кристаллогидратной массы, непрогидратировавшего вяжущего и наполнителя будет

С учетом принятых допущений получим

Средний размер капиллярной поры d, по аналогии с (12) и (35) с учетом (10) определится как

Зависимость среднего размера капиллярных пор d от степени гидратации θ для этого случая иллюстрируется рис.12 при S_x0=3000 см²/г, γ_x=3,15 г/см³.

Анализируя (40) можно видеть, что средний размер капиллярных пор d для второго варианта введения наполнителя также будет существенно меньше на начальной стадии гидратации с повышением дисперсности (увеличением b), концентрации (a), гидравлической активности (x) и плотности (z) наполнителя, а также при снижении водотвердого отношения w¢ по сравнению со структурой на исходном немодифицированном вяжущем (см.рис.12). На более поздних стадиях гидратации в связи с заменой части клинкера значение d в модифицированном вяжущем будет выше, чем в исходном "чистом" вяжущем.

Касаясь влияния тонкодисперсных наполнителей на неупорядоченность распределения пор в цементном камне, исходим из того, что при снижении многоранговости пористости (снижении среднего размера капиллярных пор при введении наполнителей) распределение пор в объеме приобретает более однородный характер.

Рис.12 Зависимость среднего размера капиллярных пор d от степени гидратации θ_x для цементных систем с введением тонкодисперсного наполнителя

путем замены части вяжущего равным объемом наполнителя при изменении водотвердого отношения (а),

дисперсности (б), объемной концентрации (в), пуццоланической активности (г) и плотности (д) наполнителя:

1,2 – система без наполнителя при w=0,3; 0,2 соответственно;

3,4 – система с тонкодисперсным наполнителем при α=0,3; β=5; z=1; ξ=0; w’ (w)=0,3 (0,43); 0,2 (0,28) соответственно;

5,6,7 – тоже при α=0,3; z=1; ξ=0; w’=0,3; β=1;5;10 соответственно;

8,9,10 – тоже при β=5; z=1; ξ=0; w’=0,3; α=0,1; 0,2; 0,3 соответственно.

Рис.12 (продолжение):

11, 12, 13 – система с тонкодисперсным наполнителем при α=0,3; β=5; z=1; w’=0,3; ξ=0; 0,5; 1 соответственно;

14, 15, 16 – тоже при α=0,3; β=5; w’=0,3; ξ=0; z(γ_f)=0,32 (1 г/см³); 0,82 (2,6 г/см³); 1,27 (4 г/см³) соответственно.

Выводы

Большое влияние на прочность цементного камня в цементных композициях наряду со структурно-механической неоднородностью кристаллогидратной связки оказывает пористость. Значительное повышение прочности может быть достигнуто модифицированием дифференциальной пористости, которая характеризуется разноразмерностью разных групп пор (многоранговостью пористости) и неупорядоченности распределения пор в объеме.

Это возможно путем введения в состав исходного вяжущего (бетонной смеси) тонкодисперсных наполнителей с более низкой удельной поверхностью, чем у вяжущего.

Использование тонкодисперсных наполнителей снижает многоранговость пористости (путем уменьшения среднего размера капиллярных пор) и неоднородность распределения пор в объеме.

Уменьшению среднего размера капиллярных пор, помимо дисперсности наполнителя способствуют такие факторы, как объемная концентрация, пуццоланическая активность и плотность наполнителя.

Список использованной литературы

1. Бальшин М.Ю. Зависимость механических свойств порошковых материалов от пористости и предельные свойства пористых металлокерамических материалов //ДАН СССР. -1949. -Т.17. -№5. -С.831-834.

2. Блох В.И. Теория упругости. -Харьков.: Изд. Харьковского Госуниверситета, 1964. -483 с. -Библиогр.: С.478-479 (46 назв.)

3. Данилович И.Ю., Сканави Н.А. Использование топливных шлаков и зол для производства строительных материалов: Учеб.пособие. -М.: Высш. шк., 1988. -72 с., ил.

4. Данюшевский В.С. Проектирование оптимальных составов тампонажных растворов. -М.: Недра, 1978. -293 с. -Библиогр.: С.276-281.

5. Данюшевский В.С., Джабаров К.А. Три вида пор в цементном камне //Неорганические материалы. -1974. -Т.10. -№2. -С.354-357.

6. Ступаченко П.П. Структурная пористость и ее связь со свойствами цементных, силикатных и гипсовых материалов //Тр.Дальневосточного политехнического ин-та. Т.63, вып.1. -Владивосток, 1964. -С.3-62.

7. Чеховский Ю.В. Понижение проницаемости бетона. -М.: Энергия, 1968. -192 с. -Библиогр.: С.176-191.

8. Чеховский Ю.В., Берлин Л.Е. О кинетике формирования поровой структуры цементного камня //Шестой междунар. конгр.по химии цемента. Т.1. -М.: Стройиздат, 1976. -С.294-297.

9. Dartsch B. Luftporengehalte ublicher Normal-betone //Betontechnische Berichte. -1974. -V10. -№16. -S.95-100.

10. Edwards R.H. Stress Concentrations Around Spheroidal Inclusions and Cavities //Journ. Appl. Mech. -1951. -№73. -pp.19-30.

11. Rice R.W. Microstructure Dependence of Mechanical Behavior of Ceramics. -New York.:-1977. -381 p. -Bibliogr.: 683 ref.

12. Ryshkewitsch E. Compression Strength of Porous Sintered Aluminia and Zirconia //J. Amer. Ceram. Soc. -1953. -V36. -№2. -pp.65-68.

13. Schiller K.K. Porosity and Strength of Brittle Solids //Mechanical Properties of Non-Metallic Brittle Materials. -London, 1958. -pp.35-49.

14. Bertolotty R.L., Fulrath R.M. Effect of Micro-mechanical Stress Concentrations on Strength of Porous Glass //Journ. of the Amer. Cer. Soc.-1967.-V50. -№11. -pp.558-562.

15. Hasselman D.P., Fulrath R.M. Micromechanical Stress Concentrations in Two-Phase Brittle-Matrix Cera-mic Composites //Journ. of the Amer.Cer.Soc.-1967.-V50. -№8. -pp.399-404.

16. Granji J.L., Maso J.S. Hardened Portland Cement Pastes, Modelization of the Microstructure and Evolu-tion Laws of Mechanical Properties. 1.Basic Results //Cem. and Concr. Res. -1984. -V14. -pp.249-256.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов