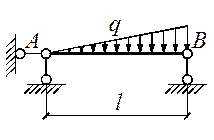Главная
Задача 1. Расчет статически неопределимых
неразрезных балок
Для статически
неопределимой неразрезной балки (рис.1),
соответствующей варианту задания,
с размерами и нагрузкой,
выбранными по шифру из табл.1,
требуется методом сил построить
эпюры М и Q.
Таблица 1
|
Номер cтроки |
Номер схемы по рис.11.1 |
q, кН/м |
а, м |
b, м |
l, м |
|
01 |
1 |
5 |
1 |
2 |
2 |
|
02 |
2 |
4 |
2 |
2 |
3 |
|
03 |
3 |
6 |
3 |
2 |
4 |
|
04 |
4 |
2 |
2 |
3 |
2 |
|
05 |
5 |
4 |
1 |
3 |
5 |
|
06 |
6 |
2 |
3 |
1 |
6 |
|
07 |
7 |
3 |
2 |
2 |
3 |
|
08 |
8 |
6 |
1 |
2 |
2 |
|
09 |
9 |
5 |
2 |
1 |
4 |
|
10 |
10 |
6 |
1 |
3 |
3 |
|
11 |
11 |
6 |
1 |
2 |
5 |
|
12 |
12 |
2 |
3 |
3 |
1 |
|
13 |
13 |
4 |
2 |
3 |
2 |
|
14 |
14 |
2 |
1 |
1 |
4 |
|
15 |
15 |
3 |
2 |
2 |
5 |
|
16 |
16 |
6 |
1 |
2 |
3 |
|
17 |
17 |
5 |
2 |
1 |
2 |
|
18 |
18 |
6 |
3 |
2 |
5 |
|
19 |
19 |
2 |
2 |
2 |
3 |
|
20 |
20 |
4 |
1 |
3 |
2 |
|
21 |
21 |
2 |
3 |
3 |
1 |
|
22 |
22 |
3 |
2 |
1 |
3 |
|
23 |
23 |
6 |
1 |
2 |
4 |
|
24 |
24 |
5 |
1 |
2 |
5 |
|
25 |
25 |
6 |
3 |
1 |
3 |
|
26 |
26 |
6 |
2 |
3 |
2 |
|
27 |
27 |
2 |
1 |
2 |
1 |
|
28 |
28 |
4 |
2 |
3 |
3 |
|
29 |
29 |
2 |
1 |
3 |
5 |
|
30 |
30 |
3 |
2 |
1 |
4 |
|
31 |
31 |
6 |
3 |
2 |
2 |
|
32 |
32 |
5 |
2 |
2 |
1 |
|
33 |
33 |
6 |
1 |
1 |
3 |
|
34 |
34 |
2 |
3 |
3 |
6 |
|
35 |
35 |
4 |
2 |
2 |
4 |
|
36 |
36 |
3 |
1 |
2 |
3 |
|
|
б |
г |
в |
а |
г |
1 схема 2 схема
3 схема 4 схема
5 схема 6 схема
7 схема 8 схема
9 схема 10 схема
11 схема 12 схема
13 схема 14 схема
15 схема 16 схема
17 схема 18 схема
19 схема 20 схема
21 схема 22 схема
23 схема 24 схема
25 схема 26 схема
27 схема 28 схема
29 схема 30 схема
31 схема 32 схема
33 схема 34 схема
35 схема 36 схема
Рис.1
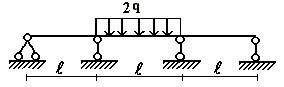
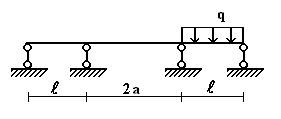
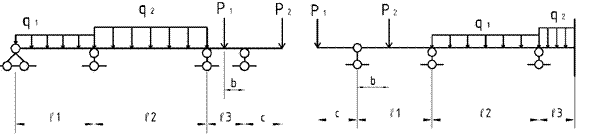
Задача 2. Расчет неразрезных балок
Для неразрезной балки (рис.2) с выбранным по шифру из табл. 2 размерами и нагрузкой,
требуется:
1) Найти с помощью уравнения трех
моментов опорные моменты и построить эпюры М
и Q
от постоянной
нагрузки q1, P1;
2) Найти фокусные отношения и
построить эпюры от последовательного загружения каждого пролета и консолей временной нагрузкой q2, P2;
3) Построить объемлющую эпюру
моментов для второго пролета (считая
слева).
Дано: EI=const.
Таблица 2
|
Номер cтроки |
Номер схемы балки по рис.2 |
q1, кН/м |
q2, кН/м |
P1, кН |
P2, кН |
l1, м |
l2, м |
l3, м |
b, м |
c, м |
|
01 |
1 |
1,0 |
1,1 |
4 |
8 |
6 |
5 |
7 |
2 |
1 |
|
02 |
2 |
1,2 |
1,3 |
8 |
4 |
7 |
6 |
9 |
3 |
2 |
|
03 |
3 |
1,4 |
0,8 |
5 |
12 |
8 |
9 |
10 |
4 |
2 |
|
04 |
4 |
1,6 |
1,7 |
9 |
5 |
9 |
10 |
6 |
3 |
2 |
|
05 |
5 |
1,8 |
1,8 |
7 |
6 |
10 |
8 |
4 |
2 |
1 |
|
06 |
6 |
1,7 |
1,2 |
6 |
14 |
11 |
7 |
8 |
3 |
1 |
|
07 |
7 |
1,1 |
0,9 |
10 |
11 |
5 |
11 |
11 |
4 |
2 |
|
08 |
8 |
1,3 |
1,4 |
3 |
9 |
12 |
12 |
12 |
3 |
3 |
|
09 |
9 |
1,5 |
1,0 |
11 |
7 |
7,5 |
13 |
5 |
2 |
3 |
|
10 |
10 |
1,9 |
1,5 |
12 |
6 |
13 |
7,5 |
6 |
3 |
2 |
|
11 |
11 |
1,0 |
1,1 |
4 |
8 |
6 |
5 |
7 |
2 |
1 |
|
12 |
12 |
1,2 |
1,3 |
8 |
4 |
7 |
6 |
9 |
3 |
2 |
|
13 |
13 |
1,4 |
0,8 |
5 |
12 |
8 |
9 |
10 |
4 |
2 |
|
14 |
14 |
1,6 |
1,7 |
9 |
5 |
9 |
10 |
6 |
3 |
2 |
|
15 |
15 |
1,8 |
1,8 |
7 |
6 |
10 |
8 |
4 |
2 |
1 |
|
16 |
16 |
1,7 |
1,2 |
6 |
14 |
11 |
7 |
8 |
3 |
1 |
|
17 |
17 |
1,1 |
0,9 |
10 |
11 |
5 |
11 |
11 |
4 |
2 |
|
18 |
18 |
1,3 |
1,4 |
3 |
9 |
12 |
12 |
12 |
3 |
3 |
|
19 |
1 |
1,5 |
1,0 |
11 |
7 |
7,5 |
13 |
5 |
2 |
3 |
|
20 |
2 |
1,9 |
1,5 |
12 |
6 |
13 |
7,5 |
6 |
3 |
2 |
|
21 |
3 |
1,0 |
1,1 |
4 |
8 |
6 |
5 |
7 |
2 |
1 |
|
22 |
4 |
1,2 |
1,3 |
8 |
4 |
7 |
6 |
9 |
3 |
2 |
|
23 |
5 |
1,4 |
0,8 |
5 |
12 |
8 |
9 |
10 |
4 |
2 |
|
24 |
6 |
1,6 |
1,7 |
9 |
5 |
9 |
10 |
6 |
3 |
2 |
|
25 |
7 |
1,8 |
1,8 |
7 |
6 |
10 |
8 |
4 |
2 |
1 |
|
26 |
8 |
1,7 |
1,2 |
6 |
14 |
11 |
7 |
8 |
3 |
1 |
|
27 |
9 |
1,1 |
0,9 |
10 |
11 |
5 |
11 |
11 |
4 |
2 |
|
28 |
10 |
1,3 |
1,4 |
3 |
9 |
12 |
12 |
12 |
3 |
3 |
|
29 |
11 |
1,5 |
1,0 |
11 |
7 |
7,5 |
13 |
5 |
2 |
3 |
|
30 |
12 |
1,9 |
1,5 |
12 |
6 |
13 |
7,5 |
6 |
3 |
2 |
|
31 |
13 |
1,0 |
1,1 |
4 |
8 |
6 |
5 |
7 |
2 |
1 |
|
32 |
14 |
1,2 |
1,3 |
8 |
4 |
7 |
6 |
9 |
3 |
2 |
|
33 |
15 |
1,4 |
0,8 |
5 |
12 |
8 |
9 |
10 |
4 |
2 |
|
34 |
16 |
1,6 |
1,7 |
9 |
5 |
9 |
10 |
6 |
3 |
2 |
|
35 |
17 |
1,8 |
1,8 |
7 |
6 |
10 |
8 |
4 |
2 |
1 |
|
36 |
18 |
1,7 |
1,2 |
6 |
14 |
11 |
7 |
8 |
3 |
1 |
|
|
б |
г |
в |
а |
г |
б |
г |
в |
а |
г |
1 схема 2 схема
3 схема 4 схема
5 схема 6 схема
7 схема 8 схема
9 схема 10 схема
11 схема 12 схема
13 схема 14 схема
15 схема 16 схема
17 схема 18 схема
Рис.2
Пояснения
к решению задачи
При решении задачи под заданной балкой
необходимо показать основную систему и эпюры моментов от нагрузки.
При построении эпюры моментов ординаты
следует откладывать со стороны растянутых волокон, т.е. положительные вниз.
Сначала надо отложить значения опорных моментов и соединить концы полученных ординат
пунктирной линией. От полученной линии опорных моментов откладываются эпюры
моментов, построенные для каждого пролета в основной системе.
Для второго пролета, для которого требуется строить
объемлющую эпюру моментов, нужно определять ординаты окончательной эпюры в
точках с интервалом 0,25l2.
Ординаты объемлющей эпюры рекомендуется определять в табличной форме.
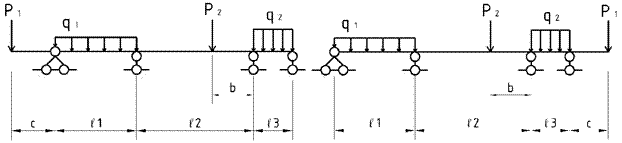
Задача 3. Расчет статически неопределимых
неразрезных балок
Для балки (рис.3), соответствующей варианту
задания, с размерами и
нагрузкой (рис.4), выбранными по
шифру из табл.3,
требуется:
1)
С помощью уравнения трех моментов найти опорные моменты и построить эпюры
изгибающих моментов М и поперечных
сил Q от постоянной нагрузки.
2)
Найти моментные фокусные отношения и построить эпюры изгибающих моментов M от
последовательного загружения каждого пролета
временной нагрузкой.
3)
Построить объемлющие (огибающие) эпюры.
4)
Рассчитать усилия в балке на ЭВМ от действия постоянной нагрузки.
Таблица 3
|
Номер cтроки |
Номер схемы балки по рис. 3 |
Номер схемы нагрузки по рис. 4 |
Временная нагрузка, qвр, кН/м |
q1, кН/м |
q2, кН/м |
P1, кН |
P2, кН |
m, кН∙м |
J1 |
J2 |
J3 |
J4 |
l1 |
l2 |
l3=l4 |
c=a |
|
01 |
1 |
0 |
1,8 |
1,0 |
1,0 |
12,0 |
6,0 |
5 |
1,0 |
2,0 |
1,0 |
2,0 |
6,0 |
8,0 |
6,0 |
1,0 |
|
02 |
2 |
9 |
1,9 |
3,0 |
2,0 |
9,0 |
8,0 |
6 |
3,0 |
2,0 |
2,0 |
3,0 |
6,0 |
7,0 |
9,0 |
2,0 |
|
03 |
3 |
8 |
2,0 |
1,0 |
2,0 |
6,0 |
4,0 |
7 |
1,0 |
1,0 |
2,0 |
2,0 |
5,0 |
7,0 |
6,0 |
2,0 |
|
04 |
4 |
7 |
2,1 |
1,0 |
3,0 |
16,0 |
8,0 |
8 |
3,0 |
3,0 |
2,0 |
1,0 |
4,0 |
6,0 |
7,0 |
1,0 |
|
05 |
5 |
6 |
2,3 |
2,0 |
1,0 |
15,0 |
8,0 |
9 |
2,0 |
1,0 |
1,0 |
2,0 |
6,0 |
8,0 |
7,0 |
2,0 |
|
06 |
1 |
5 |
2,0 |
2,0 |
3,0 |
18,0 |
4,0 |
10 |
2,0 |
2,0 |
1,5 |
1,0 |
7,0 |
8,0 |
10,0 |
2,0 |
|
07 |
2 |
4 |
2,2 |
10,0 |
1,5 |
12,0 |
4,0 |
11 |
2,0 |
2,0 |
1,0 |
1,0 |
4,0 |
5,0 |
5,0 |
1,0 |
|
08 |
3 |
3 |
2,4 |
1,5 |
1,0 |
10,0 |
5,0 |
12 |
1,5 |
2,0 |
1,0 |
1,0 |
8,0 |
4,0 |
4,0 |
1,0 |
|
09 |
4 |
2 |
2,8 |
1,5 |
1,5 |
15,0 |
6,0 |
13 |
2,0 |
1,5 |
2,0 |
2,0 |
5,0 |
6,0 |
8,0 |
2,0 |
|
10 |
5 |
1 |
1,8 |
2,0 |
3,0 |
12,0 |
15,0 |
14 |
1,0 |
2,5 |
2,0 |
3,0 |
6,0 |
5,0 |
7,0 |
1,0 |
|
11 |
1 |
0 |
1,8 |
1,0 |
1,0 |
12,0 |
6,0 |
5 |
1,0 |
2,0 |
1,0 |
2,0 |
6,0 |
8,0 |
6,0 |
1,0 |
|
12 |
2 |
9 |
1,9 |
3,0 |
2,0 |
9,0 |
8,0 |
6 |
3,0 |
2,0 |
2,0 |
3,0 |
6,0 |
7,0 |
9,0 |
2,0 |
|
13 |
3 |
8 |
2,0 |
1,0 |
2,0 |
6,0 |
4,0 |
7 |
1,0 |
1,0 |
2,0 |
2,0 |
5,0 |
7,0 |
6,0 |
2,0 |
|
14 |
4 |
7 |
2,1 |
1,0 |
3,0 |
16,0 |
8,0 |
8 |
3,0 |
3,0 |
2,0 |
1,0 |
4,0 |
6,0 |
7,0 |
1,0 |
|
15 |
5 |
6 |
2,3 |
2,0 |
1,0 |
15,0 |
8,0 |
9 |
2,0 |
1,0 |
1,0 |
2,0 |
6,0 |
8,0 |
7,0 |
2,0 |
|
16 |
1 |
5 |
2,0 |
2,0 |
3,0 |
18,0 |
4,0 |
10 |
2,0 |
2,0 |
1,5 |
1,0 |
7,0 |
8,0 |
10,0 |
2,0 |
|
17 |
2 |
4 |
2,2 |
10,0 |
1,5 |
12,0 |
4,0 |
11 |
2,0 |
2,0 |
1,0 |
1,0 |
4,0 |
5,0 |
5,0 |
1,0 |
|
18 |
3 |
3 |
2,4 |
1,5 |
1,0 |
10,0 |
5,0 |
12 |
1,5 |
2,0 |
1,0 |
1,0 |
8,0 |
4,0 |
4,0 |
1,0 |
|
19 |
4 |
2 |
2,8 |
1,5 |
1,5 |
15,0 |
6,0 |
13 |
2,0 |
1,5 |
2,0 |
2,0 |
5,0 |
6,0 |
8,0 |
2,0 |
|
20 |
5 |
1 |
1,8 |
2,0 |
3,0 |
12,0 |
15,0 |
14 |
1,0 |
2,5 |
2,0 |
3,0 |
6,0 |
5,0 |
7,0 |
1,0 |
|
21 |
1 |
0 |
1,8 |
1,0 |
1,0 |
12,0 |
6,0 |
5 |
1,0 |
2,0 |
1,0 |
2,0 |
6,0 |
8,0 |
6,0 |
1,0 |
|
22 |
2 |
9 |
1,9 |
3,0 |
2,0 |
9,0 |
8,0 |
6 |
3,0 |
2,0 |
2,0 |
3,0 |
6,0 |
7,0 |
9,0 |
2,0 |
|
23 |
3 |
8 |
2,0 |
1,0 |
2,0 |
6,0 |
4,0 |
7 |
1,0 |
1,0 |
2,0 |
2,0 |
5,0 |
7,0 |
6,0 |
2,0 |
|
24 |
4 |
7 |
2,1 |
1,0 |
3,0 |
16,0 |
8,0 |
8 |
3,0 |
3,0 |
2,0 |
1,0 |
4,0 |
6,0 |
7,0 |
1,0 |
|
25 |
5 |
6 |
2,3 |
2,0 |
1,0 |
15,0 |
8,0 |
9 |
2,0 |
1,0 |
1,0 |
2,0 |
6,0 |
8,0 |
7,0 |
2,0 |
|
26 |
1 |
5 |
2,0 |
2,0 |
3,0 |
18,0 |
4,0 |
10 |
2,0 |
2,0 |
1,5 |
1,0 |
7,0 |
8,0 |
10,0 |
2,0 |
|
27 |
2 |
4 |
2,2 |
10,0 |
1,5 |
12,0 |
4,0 |
11 |
2,0 |
2,0 |
1,0 |
1,0 |
4,0 |
5,0 |
5,0 |
1,0 |
|
28 |
3 |
3 |
2,4 |
1,5 |
1,0 |
10,0 |
5,0 |
12 |
1,5 |
2,0 |
1,0 |
1,0 |
8,0 |
4,0 |
4,0 |
1,0 |
|
29 |
4 |
2 |
2,8 |
1,5 |
1,5 |
15,0 |
6,0 |
13 |
2,0 |
1,5 |
2,0 |
2,0 |
5,0 |
6,0 |
8,0 |
2,0 |
|
30 |
5 |
1 |
1,8 |
2,0 |
3,0 |
12,0 |
15,0 |
14 |
1,0 |
2,5 |
2,0 |
3,0 |
6,0 |
5,0 |
7,0 |
1,0 |
|
31 |
1 |
0 |
1,8 |
1,0 |
1,0 |
12,0 |
6,0 |
5 |
1,0 |
2,0 |
1,0 |
2,0 |
6,0 |
8,0 |
6,0 |
1,0 |
|
32 |
2 |
9 |
1,9 |
3,0 |
2,0 |
9,0 |
8,0 |
6 |
3,0 |
2,0 |
2,0 |
3,0 |
6,0 |
7,0 |
9,0 |
2,0 |
|
33 |
3 |
8 |
2,0 |
1,0 |
2,0 |
6,0 |
4,0 |
7 |
1,0 |
1,0 |
2,0 |
2,0 |
5,0 |
7,0 |
6,0 |
2,0 |
|
34 |
4 |
7 |
2,1 |
1,0 |
3,0 |
16,0 |
8,0 |
8 |
3,0 |
3,0 |
2,0 |
1,0 |
4,0 |
6,0 |
7,0 |
1,0 |
|
35 |
5 |
6 |
2,3 |
2,0 |
1,0 |
15,0 |
8,0 |
9 |
2,0 |
1,0 |
1,0 |
2,0 |
6,0 |
8,0 |
7,0 |
2,0 |
|
36 |
1 |
5 |
2,0 |
2,0 |
3,0 |
18,0 |
4,0 |
10 |
2,0 |
2,0 |
1,5 |
1,0 |
7,0 |
8,0 |
10,0 |
2,0 |
|
|
б |
а |
в |
г |
в |
а |
г |
б |
г |
б |
а |
в |
б |
г |
в |
а |
Рис. 3. Схемы балок
Рис. 4. Схемы
нагрузок
Пояснения
к решению задачи
Неразрезной называется статически неопределимая
сплошная балка, имеющая более двух вертикальных опор и, следовательно,
перекрывающая более двух пролетов. Если своими концами она опирается на шарнирные
опоры, это простая неразрезная балка;
если имеет консоли – консольно-неразрезная; если имеет по концам защемления –
неразрезная с одним или двумя защемлениями.
Степень статической неопределимости неразрезной балки Л
зависит от вида опор и может быть определена по формулам
(1)
где 
– число
замкнутых контуров системы;
– число простых
шарниров;
– число опорных
связей (не опор).
Расчет балки по уравнению трех моментов
Расчет нужно начинать с выбора
основной системы, которую можно получить из заданной путем удаления лишних
связей, препятствующих взаимному повороту смежных сечений балки над ее опорами
(т.е. ввести во всех опорах шарниры и обозначить над ними неизвестные опорные
моменты). После этого следует приступить
к составлению системы уравнений трех моментов. В общем виде уравнение запишется
следующим образом:
где 
– произвольный
момент инерции сечения, который для расчета можно принять равным моменту
инерции одного из участков;
– приведенная
длина n-го пролета;
– левая
фиктивная опорная реакция от загружения пролета 
заданной
нагрузкой;
– правая
фиктивная опорная реакция от загружения пролета 
заданной
нагрузкой.
Величины
фиктивных опорных реакций определяются следующим образом:
где 
, 
– площади эпюр изгибающих моментов на пролетах и в
основной системе от заданной нагрузки;
– расстояние
центра тяжести эпюры 
на балке до опоры;
– расстояние от
центра тяжести эпюры на балке до
опоры;
, 
– длина пролета.
При составлении уравнения трех моментов следует
помнить, что:
1) если балка имеет консоль, то консольные ее части в
основной системе отбрасываются, а их действие заменяется известными моментами
и поперечными силами;
2) если балка имеет заделки на крайних опорах или на
одной из них, то в основной системе они условно заменяются дополнительным
пролетом бесконечно большой жесткости.
Таким образом, получив систему уравнений трех моментов
и решив ее, найдем неизвестные опорные моменты. Определив опорные моменты,
приступают к построению эпюры изгибающих моментов M, пользуясь следующей формулой:
где 
– изгибающий
момент от заданной нагрузки в простой шарнирно опертой балке;
,
– опорные
моменты, полученные при решении системы уравнений трех моментов;
–
расстояние до рассматриваемого сечения.
Построив эпюру изгибающих
моментов M, следует выполнить ее проверку, используя формулу Мора
или правило Верещагина
После проверки правильности
построения эпюр M строят эпюру поперечных сил 
как и для
статически неопределимых рам. Для
определения поперечной силы следует применить формулу
где 
– балочная
поперечная сила в сечении x в
статически определимой балке от внешней нагрузки;
Опорные реакции определяются уже по построенной эпюре
поперечных сил. Выделяется фрагмент эпюры поперечных сил в районе n-й опоры и
вырезается этот узел. Поперечные положительные силы вращают узел по часовой
стрелке.
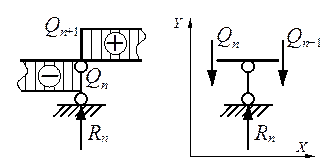
Проверка правильности построения эпюр 
и
опорных реакций проводится так же, как и для статически неопределимых рам.
Расчет балки методом моментных фокусов
При построении эпюры изгибающих моментов от временной
нагрузки следует воспользоваться методом моментных фокусных отношений.
Загружается последовательно каждый пролет и
вычисляются величины изгибающих моментов на концах каждого загруженного пролета,
для этого прежде вычисляется левые 
и правые 
фокусные
отношения по формулам.
Формула для определения левых моментно-фокусных
отношений балки
Формула
для определения правых моментно-фокусных отношений балки
Формулы для определения опорных моментов по концам
загруженного пролета
Формула для определения опорных моментов на опорах,
расположенных левее опоры 
загруженного
пролета,
Формула для определения опорных моментов на опорах,
расположенных правее опоры загруженного
пролета,
зависят от
способа закрепления балки (табл. 4).
Таблица 4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Все эпюры изгибающих моментов от временной нагрузки
необходимо построить в том же масштабе, что и эпюра изгибающих моментов от
постоянной нагрузки. Они строятся одна под другой. Для построения огибающей
эпюры изгибающих моментов нужно каждый пролет разбить на три части и подсчитать
соответствующие величины ординат изгибающих моментов. Для получения величин
максимальных ординат изгибающих моментов (
) в каждом сечении к моменту от постоянной нагрузки (
) прибавляет все положительные ординаты от временной
нагрузки, а для получения величин минимальных ординат изгибающих моментов (
) в каждом сечении к моменту от постоянной нагрузки () – все отрицательные ординаты от временной нагрузки:
(13)
(14)
Аналогично
этому находят 
и 
(15)
(16)
Ординаты и определяют
обычно в табличной форме, построение 
и 
может быть выполнено без таблицы.
Пример 1. Расчет балки методом уравнений трех
моментов
Рассчитать и построить эпюры 
и для неразрезной
балки (рис. 5)
Определяем степень статической неопределимости:
Выбираем основную систему согласно рис. 5,б. Момент на опоре 3 определяется
нагрузкой на консоли:
Вычисляем для характерных сечений каждого пролета как
для простой балки изгибающие моменты 
По вычисленным значениям строим эпюру 
в основной
системе (рис. 5,в).
По формуле (2) составляем уравнения трех моментов для
опор, соответственно приняв n=(0, 1, 2):
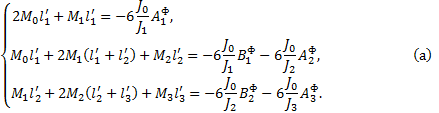
Приняв 
найдем значения
Для первого и третьего пролетов от равномерно
распределенной нагрузки, пользуясь приложением, находим:
Подставив найденные величины в систему уравнений (а),
получим:
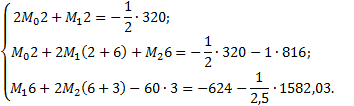
Решив
эту систему уравнений, определяем
По
формуле (3) находим моменты в
характерных сечениях балки:
По
вычисленным в характерных сечениях ординатам строится окончательная эпюра (рис.
5,г).
По
формуле (6) находим поперечные силы:
Эпюры
и , построенные по результатам расчета, представлены на
рис. 5,г, д.
По
ординатам эпюры определяем
опорные реакции (рис. 5,и).
Выполняем
кинематическую проверку правильности построения эпюры для балки.
Следует помнить, что усилия от действия обобщенной силы 
(эпюры 
показаны на
рис. 5, е, ж, з) являются безразмерными
величинами.
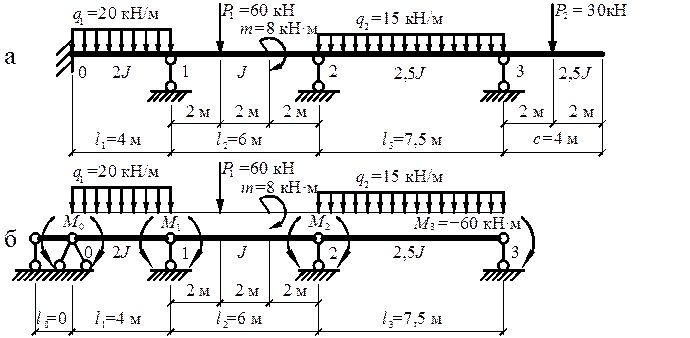
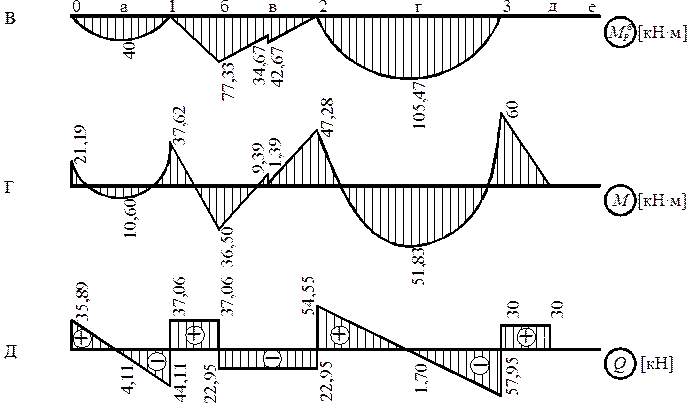
Рис.5
Выполняем
статическую проверку правильности расчета балки:
Пример 2. Расчет балки методом фокусов
Рассчитываем неразрезную балку методом фокусов на последовательное нагружение
пролетов временной нагрузкой 
По формулам (7), (8) определяем левые и правые
фокусные отношения:
Нагрузка расположена на первом пролете (рис. 6).
Согласно формулам прил. 2 фиктивные опорные реакции
составят:
По формулам (9), (10) находим:
Построение эпюры и определение
опорных реакций производится так же, как и при расчете балки по методу
уравнений трех моментов. Эпюры и опорные
реакции показаны на рис. 6, в, г, е.
Кинематическая проверка:
Кинематическую проверку желательно проводить,
используя формулу
где 
суммарная
единичная эпюра основной системы метода сил (ОСМС).
Статическая проверка:
Погрешность
менее 1%.
Рис. 6
Нагрузка
расположена на втором пролете (рис.
7).
Эпюры представлены на
рис. 7, в, г. Определение опорных
реакций показано на рис. 7, е.
Кинематическая проверка:
Статическая проверка:
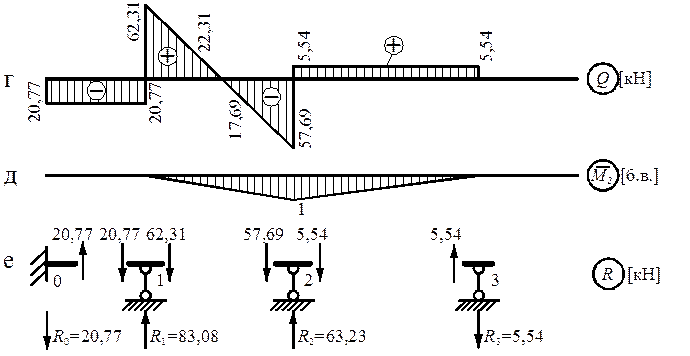
Рис. 7
Нагрузка
расположена на третьем пролете (рис.
8).
Эпюры представлены на
рис. 8, в, г. Определение опорных
реакций показано на рис. 8, е.
Кинематическая проверка:
Статическая проверка:
Рис. 8
Нагрузка
расположена на консоли (рис. 9).
Эпюры представлены на
рис. 9, б, в. Определение опорных
реакций показано на рис. 9, д.
Кинематическая проверка:
Статическая проверка:
Рис. 9
После определения моментов в характерных сечениях
балки от постоянных нагрузок и временной, расположенной в различных пролетах, в
табличной форме вычисляют 
(табл. 5):
где 
изгибающий
момент в сечении от постоянной нагрузки;
сумма положительных изгибающих моментов в сечении от временной
нагрузки (отрицательные не учитываются);
сумма отрицательных изгибающих моментов в сечении от временной
нагрузки (положительные не учитываются);
По вычисленным значениям строят огибающую эпюру
изгибающих моментов. Для этого в характерных точках для
каждого нагружения временной и постоянной нагрузками
расчетные изгибающие моменты откладывают от горизонтальной оси (отрицательные
– вверх, положительные – вниз) и
соединяют их концы (отдельно
положительных и отдельно отрицательных (рис. 10)).
Огибающую
эпюру поперечных сил строят аналогичным образом.
Таблица 5
|
№ сечения |
|
|
|
|
||||
|
на левой консоли |
на первом пролёте |
на втором пролёте |
на третьем пролёте |
на правой консоли |
||||
|
0 |
‒21,19 |
‒ |
‒36,92 |
27,69 |
‒10,82 |
6,16 |
12,66 |
‒68,93 |
|
а |
10,60 |
‒ |
18,46 |
‒13,85 |
5,41 |
‒3,08 |
34,47 |
‒6,33 |
|
1 |
‒37,62 |
‒ |
‒6,15 |
‒55,38 |
21,64 |
‒12,31 |
‒15,98 |
‒111,46 |
|
б |
36,50 |
‒ |
‒3,42 |
29,24 |
‒3,61 |
2,05 |
67,75 |
29,47 |
|
в |
‒9,39 ‒1,39 |
‒ |
‒0,68 |
33,85 |
‒28,85 |
16,41 |
40,87 48,87 |
‒38,92 ‒30,92 |
|
2 |
‒47,28 |
‒ |
2,05 |
‒41,54 |
‒54,10 |
30,78 |
‒14,45 |
‒142,92 |
|
г |
51,83 |
‒ |
1,03 |
‒20,77 |
113,58 |
‒64,61 |
166,44 |
‒33,55 |
|
3 |
‒60,00 |
‒ |
0 |
0 |
0 |
‒160,00 |
‒60,00 |
‒220,00 |
|
д |
0 |
‒ |
0 |
0 |
0 |
‒40,00 |
0 |
‒40,00 |
|
е |
0 |
‒ |
0 |
0 |
0 |
0 |
0 |
0 |
Примечание: в
числителе дано значение ординаты слева от сечения, в знаменателе – справа.
Рис. 10
Пример 3. Расчет балки методом сил
Для статически неопределимой балки (рис.11, а) требуется:
1) раскрыть ее статическую неопределимость;
2) построить эпюру изгибающих моментов от действия внешних (пролетных)
нагрузок;
3) подобрать двутавровое сечение балки из условия ее прочности;
4) определить угол поворота сечения L и прогиб балки в сечении К.
Дано: q = 6 кН/м; m = 4 кНм; а = 1,2 м; [s] = 160 МПа;
E=2∙105
Мпа.
Рис. 11. Статически неопределимая балка: а - заданная система; б - основная
система;
в -
эквивалентная система; г - грузовая эпюра Mp; д - единичная эпюра 
; е - эпюра;
ж -
окончательная эпюра M; з - эпюра от единичного момента 
; и - эпюра
от единичной силы 
Решение.
1.Вычисляем степень статической
неопределимости балки.
По условиям закрепления имеем четыре опорных реакции: две на опоре А и по одной на
опорах В и С. Для плоской системы сил можно составить только три уравнения
равновесия, поэтому степень статической неопределимости балки n = 4‑3 = 1, т.е. система один раз статически
неопределима.
2.Выбираем основную систему.
Для этого разрезаем балку над средней опорой, тем самым, устраняя
лишнюю связь, и вставляем над опорой промежуточный
шарнир. «Лишней» неизвестной в этом случае
будет изгибающий момент в опоре В, который
обозначаем Х1. На рис.11,б
показана основная система. Загружая основную систему пролетными нагрузками
и лишней неизвестной, получаем
эквивалентную систему (рис.11,в).
Достоинство принятой основной системы в том, что каждый пролет работает как
самостоятельная балка и при построении эпюр может рассматриваться отдельно.
3. Строим в основной системе эпюру
изгибающих моментов от заданной нагрузки Mp.
Рассмотрим участок АВ. Так как на этом участке нагрузок
нет, для построения эпюры достаточно
знать величины изгибающих моментов в сечениях А и В. На опоре А по условию М = m = 4 кНм; на опоре В изгибающий момент равен нулю (опорный
момент Х1 не учитываем),
эпюра моментов ограничена прямой линией.
Рассмотрим участок ВС.
Вследствие симметрии пролетной нагрузки реакции опор будут одинаковыми:
Изгибающий момент в произвольном сечении x
и эпюра
изгибающего момента ограничена квадратной параболой.
Строим эту параболу
по трем лежащим на ней точкам:
xB =
0, MB= 0;
x = 1,2 м, 
xc = 2,4 м, Mc= 0.
Эпюра
Мp
показана на рис.11, г.
4. Строим эпюру 
от единичного момента 
.
В сечениях А и С изгибающие моменты равны нулю, а в сечении В изгибающий момент равен
единице. Эпюра линейна, ее вид
показан на рис.11, д.
5.Составляем каноническое уравнение
метода сил
и вычисляем коэффициент δ11 при неизвестном. Для
этого эпюра умножается
сама на себя. Чтобы упростить
вычисления, разбиваем эпюру на два
треугольника ADB и BDC и площадь каждого из них умножаем на
ординату, расположенную в центре тяжести каждого из них (рис.11, д):
После
подстановки числовых значений имеем
Для
определения ∆1р перемножаем эпюры МP и (рис.11, г, д)
Площадь
параболического сегмента вычисляется по формуле
где
q - интенсивность распределенной
нагрузки; l - длина участка балки под нагрузкой.
Вычисляем свободный член
канонического уравнения ∆1р:
Произведя
соответствующие вычисления, получаем
Тогда каноническое уравнение принимает вид
откуда
находим
Отрицательное значение X1 говорит о том, что следует изменить направление
момента X1 на обратное.
6. Строим эпюру изгибающих моментов.
Считая момент X1 внешней
нагрузкой, можно определить опорные реакции, рассматривая каждый пролет балки
отдельно, а затем построить эпюру моментов обычным способом, как это
выполнялось для статически определимой балки. В данном случае удобнее
воспользоваться уже построенными эпюрами.
Эквивалентная система находится под действием заданных пролетных
нагрузок и вычисленного момента X1.
Следовательно, окончательная эпюра изгибающих моментов может быть представлена
суммой двух эпюр
M=Mp +
Mx1.
Первая эпюра уже построена (рис.11,г),
а вторая получается умножением ординат эпюры (рис.11,д) на вычисленное значение X1.
Эпюра 
показана на
рис.11,е. Геометрически складываем
эпюры Мp и (рис.11,г,е), суммируя
ординаты эпюр в характерных точках:
MA=4+0= 4 кНм. ME=4,32-1,47=
2,85 кНм.
MB= 0-2,93= -2,93 кНм. MC=0.
По найденным значениям М
строим окончательно эпюру изгибающих моментов (рис.11, ж).
Для проверки правильности расчетов и построения эпюры изгибающих
моментов можно использовать условие равенства нулю угла поворота смежных
сечений балки над средней опорой (перемещение по направлению отброшенной
связи). Этот угол вычисляется перемножением окончательной эпюры моментов (рис.11, ж) на эпюру (рис.11,д). При перемножении эпюру М удобно представить в виде трех
треугольников, показанных пунктирными линиями на рис.11, ж, и параболического сегмента.
Угол поворота смежных сечений балки над средней опорой вычислим методом
перемножения эпюр:
Площади эпюр и соответствующие ординаты под их центрами тяжести
определяются по соответствующим эпюрам
(рис.11, ж) и (рис.11,д).
Итак,
Полученный результат свидетельствует о том, что эпюра изгибающих моментов
построена правильно. Небольшая погрешность, не превышающая 5%, возникла в результате
округлений.
7. Подбираем сечение балки по условию
прочности.
При
изгибе условие прочности имеет вид
По эпюре М (рис.11, ж) находим максимальный момент 
= 4 кНм, а по условию задачи [σ] = 160 МПа. Подставляя эти числа в последнюю
формулу, получим величину требуемого момента сопротивления двутавра:
По таблицам сортамента прокатной стали подбираем номер двутавра и выписываем его геометрические характеристики: двутавр №10, Wx= 39,7 cм3,
Jx = 198 см4.
(Момент
сопротивления подобранного двутавра больше требуемого
расчетного, но меньшего размера в таблице нет, поэтому принимаем двутавр №10).
8. Определяем перемещения.
Определяем угол поворота сечения L.
Для этого приложим в сечении L основной системы единичный момент 
и построим
эпюру моментов 
(рис.11,з). Угол поворота сечения L вычисляем, перемножая эпюры М и (рис.11, ж,з):
Определяем прогиб в сечении К.
Приложим в сечении К основной системы
единичную силу 
и построим от нее
эпюру моментов 
(рис.11,и). Так как сила 
приложена в
середине пролета AB, опорные реакции будут равны:
RA = RB = 0,5.
Определяем
моменты в характерных точках участка АВ:
MA = 0; МK = 0,5∙1,8 = 0,9 м; MB = 0.
Прогиб в сечении К
вычисляется перемножением эпюр М и (рис.11,ж,и). Площадь
при этом берем с эпюры М, а
соответствующая ордината на эпюре 
равна величине средней линии трапеции, то есть алгебраической
полусумме ее оснований:
Результат получен со знаком плюс, прогиб направлен в сторону приложенной
единичной силы, то есть вниз.
Приложение
|
Схема нагрузки |
|
|
|
|
При u
= v
= 0,5
|
При u = v = 0,5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При u = v = 0,5
|
При u = v = 0,5
|
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Теория машин и механизмов
