Главная
Задача 1. Расчет плоских статически неопределимых рам на
устойчивость методом перемещений
Для статически неопределимой рамы (рис.1) с выбранными
из табл.1 размерами и нагрузкой и характеристикой жесткости требуется
определить значения критических сил и расчетных длин, используя метод перемещений.
Порядок выполнения работы:
1) Записать выражение
для критических параметров всех сжимаемых стержней рамы используя выражение
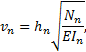
где n –
номер сжимаемого стержня.
Все параметры vn выразить через v0, принимая за последний любой из параметров v.
2) Выбрать
основную систему метода перемещений путем введения в заданную расчетную схему дополнительных
угловых и линейных связей по направлению возможных угловых и линейных смещений
узлов.
3) Составить
уравнение устойчивости в общем виде.
4) Построить в основной системе эпюры изгибающих
моментов от единичных смещений по направлениям введенных дополнительных связей,
используя таблицы реакций прил. 1 и 2.
5) С помощью построенных эпюр определить реакции в
дополнительных связях от заданных единичных смещений и представить уравнение
устойчивости в развернутом виде.
6) Решить уравнение устойчивости путем подбора наименьшего
критического параметра vкр при помощи таблиц трансцедентных
функций (прил. 3).
7) Определить критические силы Fкр и расчетные длины l0 для всех
сжатых стоек расчетной схемы по найденным значениям критических параметров vn,кр по формулам:
где
hn – длина сжатой
стойки рамы.
Таблица 1
|
Номер cтроки |
Номер схемы по рис.1 |
EI1, кН/м2 |
|
l, м |
h1, м |
h2, м |
|
|
1 |
1 |
5000 |
3,0 |
4,2 |
3,2 |
4,0 |
1,21 |
|
2 |
2 |
5500 |
2,4 |
4,8 |
4,0 |
5,0 |
0,81 |
|
3 |
3 |
6000 |
2,0 |
5,6 |
3,8 |
5,8 |
1,44 |
|
4 |
4 |
6500 |
1,6 |
6,0 |
4,4 |
6,4 |
2,89 |
|
5 |
5 |
7000 |
1,8 |
4,0 |
2,8 |
4,6 |
2,56 |
|
6 |
6 |
7500 |
2,6 |
6,4 |
5,6 |
6,2 |
1,69 |
|
7 |
7 |
8000 |
2,2 |
4,4 |
4,2 |
4,8 |
1,96 |
|
8 |
8 |
8500 |
2,8 |
5,2 |
4,6 |
5,4 |
0,64 |
|
9 |
9 |
9000 |
1,5 |
5,4 |
4,0 |
5,0 |
0,49 |
|
10 |
10 |
9500 |
2,5 |
5,8 |
4,2 |
5,6 |
3,24 |
|
11 |
1 |
5000 |
3,0 |
4,2 |
3,2 |
4,0 |
1,21 |
|
12 |
2 |
5500 |
2,4 |
4,8 |
4,0 |
5,0 |
0,81 |
|
13 |
3 |
6000 |
2,0 |
5,6 |
3,8 |
5,8 |
1,44 |
|
14 |
4 |
6500 |
1,6 |
6,0 |
4,4 |
6,4 |
2,89 |
|
15 |
5 |
7000 |
1,8 |
4,0 |
2,8 |
4,6 |
2,56 |
|
16 |
6 |
7500 |
2,6 |
6,4 |
5,6 |
6,2 |
1,69 |
|
17 |
7 |
8000 |
2,2 |
4,4 |
4,2 |
4,8 |
1,96 |
|
18 |
8 |
8500 |
2,8 |
5,2 |
4,6 |
5,4 |
0,64 |
|
19 |
9 |
9000 |
1,5 |
5,4 |
4,0 |
5,0 |
0,49 |
|
20 |
10 |
9500 |
2,5 |
5,8 |
4,2 |
5,6 |
3,24 |
|
21 |
1 |
5000 |
3,0 |
4,2 |
3,2 |
4,0 |
1,21 |
|
22 |
2 |
5500 |
2,4 |
4,8 |
4,0 |
5,0 |
0,81 |
|
23 |
3 |
6000 |
2,0 |
5,6 |
3,8 |
5,8 |
1,44 |
|
24 |
4 |
6500 |
1,6 |
6,0 |
4,4 |
6,4 |
2,89 |
|
25 |
5 |
7000 |
1,8 |
4,0 |
2,8 |
4,6 |
2,56 |
|
26 |
6 |
7500 |
2,6 |
6,4 |
5,6 |
6,2 |
1,69 |
|
27 |
7 |
8000 |
2,2 |
4,4 |
4,2 |
4,8 |
1,96 |
|
28 |
8 |
8500 |
2,8 |
5,2 |
4,6 |
5,4 |
0,64 |
|
29 |
9 |
9000 |
1,5 |
5,4 |
4,0 |
5,0 |
0,49 |
|
30 |
10 |
9500 |
2,5 |
5,8 |
4,2 |
5,6 |
3,24 |
|
31 |
1 |
5000 |
3,0 |
4,2 |
3,2 |
4,0 |
1,21 |
|
32 |
2 |
5500 |
2,4 |
4,8 |
4,0 |
5,0 |
0,81 |
|
33 |
3 |
6000 |
2,0 |
5,6 |
3,8 |
5,8 |
1,44 |
|
34 |
4 |
6500 |
1,6 |
6,0 |
4,4 |
6,4 |
2,89 |
|
35 |
5 |
7000 |
1,8 |
4,0 |
2,8 |
4,6 |
2,56 |
|
36 |
6 |
7500 |
2,6 |
6,4 |
5,6 |
6,2 |
1,69 |
|
|
а |
в |
г |
|
б |
а |
г |
Схема 1 Схема 2
Схема 3 Схема 4
Схема 5 Схема 6
Схема 7 Схема 8
Схема 9 Схема 10
Рис.1
Задача 2. Расчет плоских статически неопределимых рам на
устойчивость методом перемещений
Для статически неопределимой рамы (рис.2) с выбранными
из табл. 2 размерами и нагрузкой требуется определить значения критических сил,
используя метод перемещений.
Таблица 2
|
Номер cтроки |
Номер схемы по рис.2 |
l1, м |
l2, м |
h1, м |
h2, м |
|
|
|
1 |
1 |
4 |
13 |
7 |
4 |
1,2 |
0,9 |
|
2 |
2 |
5 |
12 |
10 |
5 |
1,3 |
0,8 |
|
3 |
3 |
6 |
11 |
9 |
6 |
1,4 |
0,7 |
|
4 |
4 |
7 |
10 |
8 |
7 |
1,5 |
0,6 |
|
5 |
5 |
8 |
9 |
7 |
8 |
1,6 |
0,5 |
|
6 |
6 |
9 |
8 |
6 |
9 |
1,7 |
1,2 |
|
7 |
7 |
10 |
7 |
5 |
10 |
1,8 |
1,4 |
|
8 |
8 |
11 |
6 |
8 |
7 |
1,9 |
1,5 |
|
9 |
9 |
12 |
5 |
11 |
4 |
2,0 |
1,6 |
|
10 |
10 |
13 |
4 |
12 |
3 |
2,1 |
1,8 |
|
11 |
11 |
6 |
8 |
5 |
6 |
0,4 |
0,4 |
|
12 |
12 |
7 |
5 |
11 |
10 |
2,3 |
1,0 |
|
13 |
13 |
12 |
11 |
7 |
9 |
0,8 |
1,1 |
|
14 |
14 |
4 |
3 |
6 |
4 |
0,5 |
1,3 |
|
15 |
15 |
10 |
9 |
13 |
8 |
2,4 |
1,7 |
|
16 |
16 |
8 |
13 |
10 |
12 |
0,9 |
1,9 |
|
17 |
17 |
6 |
4 |
9 |
11 |
0,6 |
2,1 |
|
18 |
18 |
9 |
7 |
4 |
5 |
2,5 |
2,0 |
|
19 |
19 |
11 |
10 |
8 |
7 |
2,2 |
2,2 |
|
20 |
20 |
5 |
6 |
12 |
13 |
0,7 |
2,3 |
|
21 |
1 |
7 |
10 |
8 |
7 |
1,5 |
0,6 |
|
22 |
2 |
8 |
9 |
7 |
8 |
1,6 |
0,5 |
|
23 |
3 |
9 |
8 |
6 |
9 |
1,7 |
1,2 |
|
24 |
4 |
10 |
7 |
5 |
10 |
1,8 |
1,4 |
|
25 |
5 |
11 |
6 |
8 |
7 |
1,9 |
1,5 |
|
26 |
6 |
12 |
5 |
11 |
4 |
2,0 |
1,6 |
|
27 |
7 |
13 |
4 |
12 |
3 |
2,1 |
1,8 |
|
28 |
8 |
6 |
8 |
5 |
6 |
0,4 |
0,4 |
|
29 |
9 |
7 |
5 |
11 |
10 |
2,3 |
1,0 |
|
30 |
10 |
12 |
11 |
7 |
9 |
0,8 |
1,1 |
|
31 |
11 |
6 |
4 |
9 |
11 |
0,6 |
2,1 |
|
32 |
12 |
9 |
7 |
4 |
5 |
2,5 |
2,0 |
|
33 |
13 |
11 |
10 |
8 |
7 |
2,2 |
2,2 |
|
34 |
14 |
5 |
6 |
12 |
13 |
0,7 |
2,3 |
|
35 |
15 |
7 |
10 |
8 |
7 |
1,5 |
0,6 |
|
36 |
16 |
8 |
9 |
7 |
8 |
1,6 |
0,5 |
|
|
а |
в |
г |
б |
а |
г |
в |
I1 – момент инерции ригеля, I2 – момент инерции стойки.
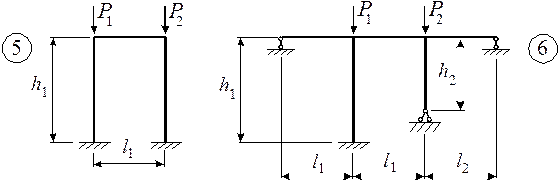
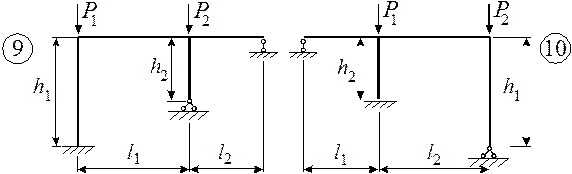
Рис. 2
Пояснения к решению задачи 2.
При расчете рам на устойчивость необходимо
использовать метод перемещений. По канонической форме метода перемещений за
основную систему принимаем раму с введенными фиктивными защемлениями жестких узлов
и дополнительными против смещения опорными стержнями.
Построение единичных эпюр моментов для сжатых стоек
следует проводить по специальным таблицам, а для ригелей – по обычным таблицам
метода перемещений.
Коэффициенты канонических уравнений определяются из
рассмотрения равновесия соответствующих узлов и равновесия ригеля рамы. Эти
коэффициенты будут включать в себя некоторые функции 
и 
от параметров
где Pi и Pk –
силы, действующие вдоль стоек hi и hk; EIi и EIk –
жесткости стоек. Между параметрами ni и nk
необходимо установить связь.
Задача заключается в определении наименьшего критического значения
параметра vn=v.
Условие равенства нулю полных реакций в
введенных связях будет выражено:
Если система получает искривление, перемещения Zi отличны от нуля, что возможно только в случае, когда
определитель D(v) из коэффициентов при неизвестных Zi равен нулю.
Здесь 
–
"единичные" упругие реакции. В значения войдут
выражения функций от параметра v(φ1, φ2, φ3, φ4, η1, η2). Раскрыв определитель D(v), получим трансцендентное уравнение относительно v.
Это уравнение можно решить двумя способами. По первому
способу уравнение решается подбором в следующей последовательности: а) задаются
значением vk ; б) по
вычисленному соотношению определяется vi ; в)
по таблицам находятся значения необходимых коэффициентов (функций φn(vi), φm(vk), …); г) найденные значения функций подставляются в
уравнение устойчивости. По второму способу можно воспользоваться программным
продуктом MathCAD 7.0 версии и выше.
Если данные значения функций не удовлетворяют
уравнению устойчивости, то задаются другим значением vk и все вычисления повторяются.
Эта операция продолжается до тех пор, пока принятые значения не будут удовлетворять
уравнению устойчивости. Тогда по формулам
определяются значения критических сил.
Приложения
Приложение 1. Таблицы
реакций и усилий в изгибаемых стержнях
от единичных смещений связей и внешних
воздействий
Приложение 2. Таблица реакций и усилий в сжато-изогнутых
стержнях от
единичных смещений связей
Приложение 3. Таблица значений трансцедентных функций метода
перемещений для сжато-изогнутых стержней
|
v |
φ1(v) |
φ2(v) |
φ3(v) |
φ4(v) |
η1(v) |
η2(v) |
|
0,0 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
|
0,2 |
0,9973 |
0,9980 |
1,0009 |
0,9992 |
0,9840 |
0,9959 |
|
0,4 |
0,9895 |
0,9945 |
1,0026 |
0,9973 |
0,9362 |
0,9840 |
|
0,6 |
0,9856 |
0,9881 |
1,0061 |
0,9941 |
0,8557 |
0,9641 |
|
0,8 |
0,9566 |
0,9787 |
1,0111 |
0,9895 |
0,7432 |
0,9362 |
|
1,0 |
0,9313 |
0,9662 |
1,0172 |
0,9832 |
0,5980 |
0,8999 |
|
|
|
|
|
|
|
|
|
1,1 |
0,9194 |
0,9590 |
1,0209 |
0,9798 |
0,5131 |
0,8789 |
|
1,2 |
0,8998 |
0,9511 |
1,0251 |
0,9751 |
0,4198 |
0,8557 |
|
1,3 |
0,8814 |
0,9424 |
1,0298 |
0,9715 |
0,3181 |
0,8307 |
|
1,4 |
0,8613 |
0,9329 |
1,0348 |
0,9669 |
0,2080 |
0,8035 |
|
1,5 |
0,8393 |
0,9226 |
1,0403 |
0,9619 |
0,0893 |
0,7743 |
|
1,6 |
0,8153 |
0,9116 |
1,0463 |
0,9566 |
-0,0380 |
0,7432 |
|
|
|
|
|
|
|
|
|
1,7 |
0,7891 |
0,8998 |
1,0529 |
0,9509 |
-0,1742 |
0,7100 |
|
1,8 |
0,7609 |
0,8871 |
1,0600 |
0,9448 |
-0,3191 |
0,6747 |
|
1,9 |
0,7297 |
0,8735 |
1,0676 |
0,9382 |
-0,4736 |
0,6374 |
|
2,0 |
0,6961 |
0,8590 |
1,0760 |
0,9313 |
-0,6372 |
0,5980 |
|
2,1 |
0,6597 |
0,8437 |
1,0850 |
0,9240 |
-0,8103 |
0,5565 |
|
2,2 |
0,6202 |
0,8273 |
1,0946 |
0,9164 |
-0,9931 |
0,5131 |
|
|
|
|
|
|
|
|
|
2,3 |
0,5772 |
0,8099 |
1,1050 |
0,9083 |
-1,1861 |
0,4675 |
|
2,4 |
0,5304 |
0,7915 |
1,1164 |
0,8998 |
-1,3895 |
0,4198 |
|
2,5 |
0,4793 |
0,7720 |
1,1286 |
0,8909 |
-1,6040 |
0,3701 |
|
2,6 |
0,4234 |
0,7513 |
1,1417 |
0,8814 |
-1,8299 |
0,3181 |
|
2,7 |
0,3621 |
0,7294 |
1,1559 |
0,8716 |
-2,0679 |
0,5565 |
|
2,8 |
0,2944 |
0,7064 |
1,1712 |
0,8613 |
-2,3189 |
0,2080 |
|
|
|
|
|
|
|
|
|
2,9 |
0,2195 |
0,6819 |
1,1878 |
0,8506 |
-2,5838 |
0,1498 |
|
3,0 |
0,1361 |
0,6560 |
1,2057 |
0,8393 |
-2,8639 |
0,0893 |
|
3,1 |
0,0424 |
0,6287 |
1,2252 |
0,8275 |
-3,1609 |
0,0207 |
|
3,2 |
-0,0635 |
0,5997 |
1,2463 |
0,8153 |
-3,4763 |
-0,0380 |
|
3,3 |
-0,1847 |
0,5691 |
1,2691 |
0,8024 |
-3,8147 |
-0,1051 |
|
3,4 |
-0,3248 |
0,5366 |
1,2940 |
0,7891 |
-4,1781 |
-0,1742 |
|
3,5 |
-0,4894 |
0,5021 |
1,3212 |
0,7751 |
-4,5727 |
-0,2457 |
|
3,6 |
-0,6862 |
0,4656 |
1,3508 |
0,7609 |
-5,0062 |
-0,3191 |
|
3,7 |
-0,9270 |
0,4265 |
1,3834 |
0,7457 |
-5,4903 |
-0,3951 |
|
3,8 |
-1,2303 |
0,3850 |
1,4191 |
0,7297 |
-6,0436 |
-0,4736 |
|
3,9 |
-1,6268 |
0,3407 |
1,4584 |
0,7133 |
-6,6968 |
-0,5542 |
|
4,0 |
-2,1726 |
0,2933 |
1,5018 |
0,6961 |
-7,5058 |
-0,6372 |
|
|
|
|
|
|
|
|
|
4,1 |
-2,9806 |
0,2424 |
1,5501 |
0,6783 |
-8,5836 |
-0,7225 |
|
4,2 |
-4,3155 |
0,1877 |
1,6036 |
0,6597 |
-10,196 |
-0,8103 |
|
4,3 |
-6,9949 |
0,1288 |
1,6637 |
0,6404 |
-13,158 |
-0,9004 |
|
4,4 |
-15,330 |
0,0648 |
1,7310 |
0,6202 |
-27,781 |
-0,9931 |
|
4,5 |
227,80 |
-0,0048 |
1,8070 |
0,5991 |
221,05 |
-1,0884 |
|
4,6 |
14,669 |
-0,0808 |
1,8933 |
0,5772 |
7,6160 |
-1,1861 |
|
|
|
|
|
|
|
|
|
4,7 |
7,8185 |
-0,1646 |
1,9919 |
0,5543 |
0,4553 |
-1,2865 |
|
4,8 |
5,4020 |
-0,2572 |
2,1056 |
0,5304 |
-2,2777 |
-1,3895 |
|
4,9 |
4,1463 |
-0,3612 |
2,2377 |
0,5054 |
-3,8570 |
-1,4954 |
|
5,0 |
3,3615 |
-0,4772 |
2,3924 |
0,4793 |
-4,9718 |
-1,6040 |
|
5,1 |
2,8130 |
-0,6100 |
2,5757 |
0,4520 |
-5,8570 |
-1,7155 |
|
5,2 |
2,3986 |
-0,7630 |
2,7961 |
0,4234 |
-6,6147 |
-1,8299 |
|
|
|
|
|
|
|
|
|
5,3 |
2,0668 |
-0,9423 |
3,0648 |
0,3935 |
-7,2965 |
-1,9473 |
|
5,4 |
1,7884 |
-1,1563 |
3,3989 |
0,3621 |
-7,9316 |
-2,0679 |
|
5,5 |
1,5455 |
-1,4181 |
3,8234 |
0,3291 |
-8,5379 |
-2,1917 |
|
5,6 |
1,3265 |
-1,7481 |
4,3794 |
0,2944 |
-9,1268 |
-2,3189 |
|
5,7 |
1,1235 |
-2,180 |
5,1346 |
0,2580 |
-9,7056 |
-2,4495 |
|
5,8 |
0,9302 |
-2,7777 |
6,2140 |
0,2195 |
-10,283 |
-2,5838 |
|
|
|
|
|
|
|
|
|
5,9 |
0,7421 |
-3,6678 |
7,8726 |
0,1790 |
-10,863 |
-2,7218 |
|
6,0 |
0,5551 |
-5,1589 |
10,727 |
0,1361 |
-11,445 |
-2,8639 |
|
6,1 |
0,3659 |
-8,2355 |
16,739 |
0,0906 |
-12,038 |
-3,0102 |
|
6,2 |
0,1700 |
-18,591 |
37,308 |
0,0424 |
-12,643 |
-3,1609 |
|
2π |
0,0000 |
-∞ |
+∞ |
0,0000 |
-13,033 |
-3,2898 |
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Теория машин и механизмов
