Главная
Задача 1. Расчет статически
неопределимых арок
Для заданной статически неопределимой арки (рис.1) с
выбранными по шифру из таблицы 1 размерами и нагрузкой при EI=const требуется
построить эпюры изгибающих моментов, поперечных и продольных сил.
Схему загружения арки
принять в виде, указанном на рис.2.
Таблица 1
|
Номер строки |
Схема по рис.1 |
l, м |
α |
f/l |
q1, кН/м |
q2, кН/м |
Очертание оси арки |
|
01 |
1 |
16 |
0,25 |
0,20 |
2 |
0 |
Квадратная парабола |
|
02 |
2 |
18 |
0,30 |
0,30 |
0 |
3 |
Окружность |
|
03 |
3 |
20 |
0,35 |
0,16 |
4 |
0 |
Квадратная парабола |
|
04 |
4 |
22 |
0,40 |
0,25 |
0 |
5 |
Окружность |
|
05 |
5 |
24 |
0,45 |
0,45 |
6 |
0 |
Квадратная парабола |
|
06 |
6 |
26 |
0,50 |
0,32 |
0 |
6 |
Окружность |
|
07 |
7 |
28 |
0,55 |
0,15 |
3 |
0 |
Квадратная парабола |
|
08 |
8 |
30 |
0,60 |
0,18 |
0 |
4 |
Окружность |
|
09 |
9 |
32 |
0,70 |
0,14 |
0 |
2 |
Квадратная парабола |
|
10 |
10 |
34 |
0,65 |
0,22 |
5 |
0 |
Окружность |
|
11 |
11 |
16 |
0,25 |
0,20 |
2 |
0 |
Квадратная парабола |
|
12 |
12 |
18 |
0,30 |
0,30 |
0 |
3 |
Окружность |
|
13 |
13 |
20 |
0,35 |
0,16 |
4 |
0 |
Квадратная парабола |
|
14 |
14 |
22 |
0,40 |
0,25 |
0 |
5 |
Окружность |
|
15 |
15 |
24 |
0,45 |
0,45 |
6 |
0 |
Квадратная парабола |
|
|
в |
г |
б |
а |
в |
б |
а |
1 схема
2 схема
3 схема
4 схема
5 схема
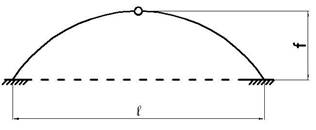
6 схема
7 схема
8 схема
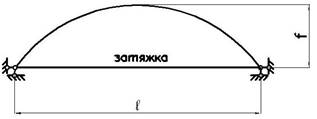
9 схема
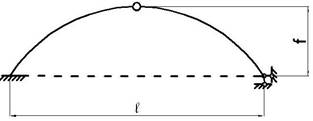
10 схема
11 схема
12 схема
13 схема
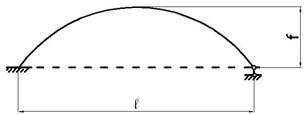
14 схема
15 схема
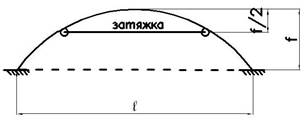
Рис.1
Рис.2
Методические указания
В строительстве применяются в основном статически
неопределимые арки двух видов: двухшарнирные и бесшарнирные.
Расчёт производится методом сил. В арках для
вычисления перемещений в основной системе способ Верещагина вследствие криволинейности всех эпюр неприменим. Непосредственное
интегрирование формулы Мора сложно, а порой и невозможно. Поэтому обычно
интегрирование заменяется суммированием по участкам арки, например, по формуле
Симпсона (способ параболических трапеций).
Для двухшарнирной арки,
являющейся один раз статически неопределимой системой, основную систему
получают, отбрасывая горизонтальную связь в одной из опор. Бесшарнирная
арка является трижды статически неопределимой системой, для неё основную
систему выбирают с введением жёстких консолей, свободные концы которых
совпадают с упругим центром.
Способ упругого центра позволяет записать три
независимых канонических уравнения, каждое из которых содержит только одно
неизвестное.
Уравнение оси арки задаётся в двух вариантах:
1) при очертании оси по параболе
2)
при очертании оси по окружности
Пример
расчета статически неопределимой арки
Для
параболической двухшарнирной арки постоянного
поперечного сечения с заданными размерами и нагрузкой требуется построить эпюры
изгибающих моментов, поперечных и продольных сил (рис.3).
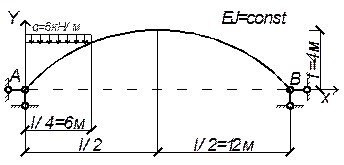
Рис.3
Решение.
Ось
арки очерчена по квадратной параболе 
отнесенной к
началу координат на левой опоре.
Степень
статической неопределимости арки n=3m-Ш=3∙3-8=1.
Основную систему получаем,
принимая за лишнее неизвестное реакцию распора (рис.4).
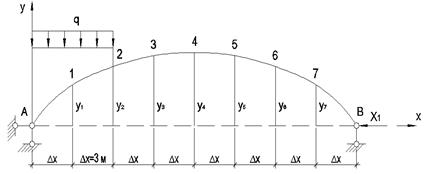
Рис.4
Каноническое уравнение метода сил:
Продольными и поперечными силами при определении
коэффициентов канонического уравнения пренебрегаем.
Рассмотрим основную систему в двух состояниях: при загружении единичной силой Х1=1 и внешней нагрузкой (рис.5).
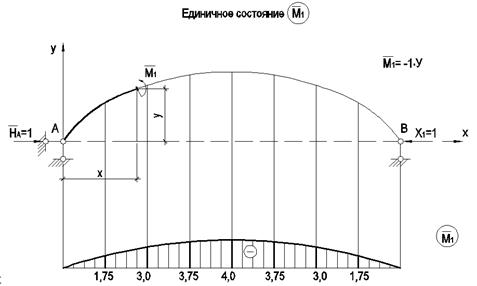
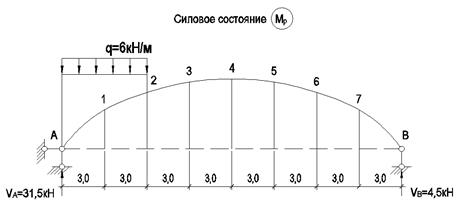
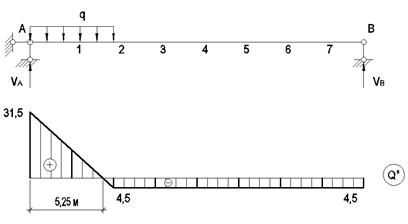
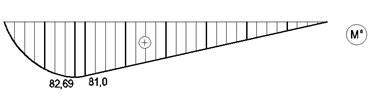
Рис.5
Изгибающий момент в основной системе от внешней
нагрузки совпадает с моментом однопролётной балки того же пролёта и такой же
нагрузки:
Построим балочные эпюры изгибающих моментов и
поперечных сил 
(рис.5).
При вычислении перемещений 
и 
используем
интеграл Мора:
Внесём найденные зависимости в интеграл:
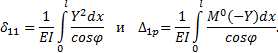
Произведём замену:
Тогда имеем:
Полученные интегралы невозможно вычислить точно,
поэтому интегрирование заменим суммированием. Разобьём пролёт арки на восемь
равных частей ∆x=3 м и, используя правило Симпсона, получим следующие
выражения для и :
Дальнейший расчёт приведён в таблице 2-4.
Подставив численные значения величин ZX и ZP,
получим следующие значения перемещений:
Горизонтальная составляющая опорной реакции
Внутренние силы в двухшарнирной
арке находят по формулам:
Эпюры M, Q и N показаны на рис.6.
Таблица 2
|
Номер сечения |
А |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
В |
|
x, м |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y, м |
0 |
1,75 |
3,0 |
3,75 |
4,0 |
3,75 |
3,0 |
1,75 |
0 |
|
|
0,667 |
0,5 |
0,333 |
0,167 |
0 |
-0,167 |
-0,333 |
-0,5 |
-0,667 |
|
sinφ |
0,5544 |
0,4488 |
0,3173 |
0,165 |
0 |
-0,165 |
-0,3173 |
-0,4488 |
-0,5544 |
|
cosφ |
0,832 |
0,8936 |
0,9483 |
0,9863 |
1,0 |
0,9863 |
0,9483 |
0,8936 |
0,832 |
|
|
0 |
67,5 |
81,0 |
67,5 |
54,0 |
40,5 |
27,0 |
13,5 |
0 |
Таблица 3
|
Номер сечения |
А |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
В |
|
|
31,5 |
13,5 |
-4,5 |
-4,5 |
-4,5 |
-4,5 |
-4,5 |
-4,5 |
-4,5 |
|
|
-17,464 |
-6,0588 |
1,428 |
0,752 |
0 |
-0,752 |
-1,428 |
-2,02 |
-2,495 |
|
|
26,208 |
12,064 |
-4,267 |
-4,438 |
-4,5 |
-4,438 |
-4,267 |
-4,021 |
-3,744 |
|
|
0 |
3,427 |
9,491 |
14,258 |
16,0 |
14,258 |
9,491 |
3,427 |
0 |
|
|
0 |
-132,19 |
-256,248 |
-256,641 |
-216,0 |
-153,985 |
-85,416 |
-26,438 |
0 |
|
|
0 |
28,07 |
48,12 |
60,15 |
64,16 |
60,15 |
48,12 |
28,07 |
0 |
Таблица 4
|
Номер сечения |
А |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
В |
|
|
8,893 |
7,199 |
5,089 |
2,647 |
0 |
-2,647 |
-5,089 |
-7,199 |
-8,893 |
|
|
13,345 |
14,333 |
15,211 |
15,82 |
16,04 |
15,82 |
15,211 |
14,333 |
13,345 |
|
|
0 |
39,43 |
32,88 |
7,35 |
-10,16 |
-19,65 |
-21,12 |
-14,57 |
0 |
|
|
17,315 |
4,865 |
-9,356 |
-7,085 |
-4,5 |
-1,791 |
0,822 |
3,178 |
5,149 |
|
|
-30,809 |
-20,392 |
-13,783 |
-15,068 |
-16,04 |
-16,572 |
-16,639 |
-16,353 |
-15,84 |
|
Кинематическая проверка
|
0 |
-77,219 |
-104,018 |
-27,945 |
40,64 |
74,711 |
66,814 |
28,533 |
0 |
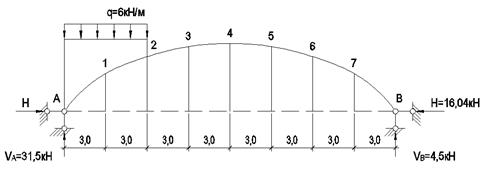
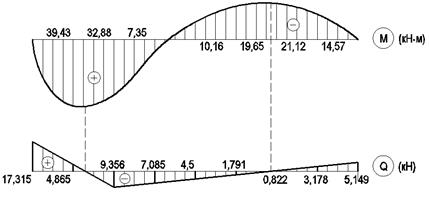
Рис.6
Выполним кинематическую проверку эпюры
изгибающих моментов. Суть проверки заключается в том, что перемещение по
направлению неизвестного x1 должно
равняться нулю.
где М
– эпюра изгибающих моментов для статически неопределимой арки; 
- эпюра моментов
от единичной силы x1 = 1 в
основной системе (статически определимой).
Произведём замену: 
, тогда
Данный интеграл найден по правилу
Симпсона:
Результаты расчёта приведены в таб.4,
последняя строка (кинематическая проверка).
Погрешность составляет всего
Допустимой можно считать невязку до 2%.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Теория машин и механизмов
