Главная

 

Задача 1. Статически определимые стержневые системы, работающие на растяжение-сжатие.

Два стальных (1 и 2) стержня, шарнирно соединенных в точке А, находятся под действием силы Р (рис.1). Первый стержень имеет длину с и площадь поперечного сечения A, второй - длину а и площадь – 2A.

1) Найти величину нормальных напряжений, действующих в стержнях.

2) Найти абсолютную и относительную деформации стержней.

Данные взять из табл.1.

Таблица 1

 

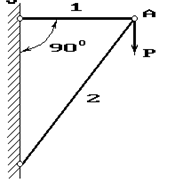
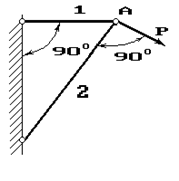
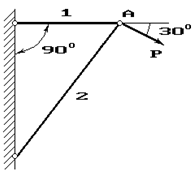
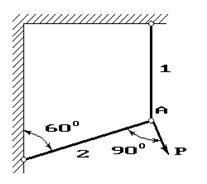
1 схема                    2 схема                           3 схема

 

4 схема                             5 схема                                  6 схема

 

7 схема                             8 схема                                  9 схема

 

10 схема                             11 схема                       12 схема

 

13 схема                             14 схема                                  15 схема

 

 

16 схема                             17 схема                                  18 схема

 

19 схема                             20 схема                       21 схема

 

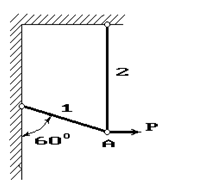
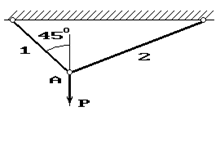
22 схема                             23 схема                              24 схема

 

 

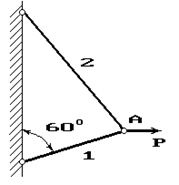
25 схема                             26 схема                                  27 схема

 

28 схема                              29 схема                                              30 схема

 

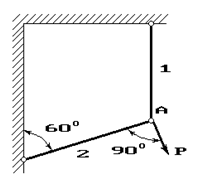
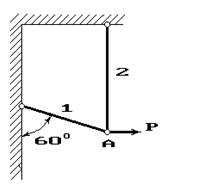
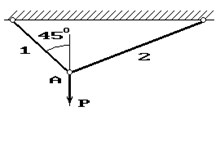
31 схема                           32 схема                                33 схема

 

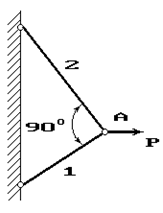
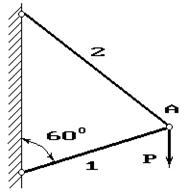
34 схема                              35 схема                                  36 схема

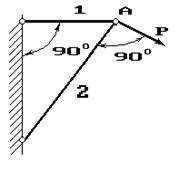
Рис. 1

 

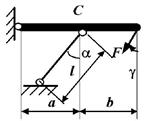
Задача 2. Определение грузоподъемности статически определимой стержневой конструкции, работающей на растяжение-сжатие

Исходные данные к задаче выбираются по табл. 2 и схемам на рис. 2

1. Нарисуйте схему конструкции в масштабе. На рисунке поставьте размеры конструкции в численном виде.

2. Найдите продольные силы в стержнях конструкции, используя метод сечений. Если на расчетной схеме стержень выделен жирной линией, то этот стержень следует считать абсолютно жестким. (Он не деформируется и продольная сила в нем равна нулю).

3. Найдите напряжения в стержнях, выразив их через неизвестную нагрузку.

4. Из условия прочности наиболее напряженного стержня найдите допускаемое значение нагрузки.

5. Найдите перемещение узла С и покажите его на плане перемещений.

 

Таблица 2

 

 

       1 схема                              2 схема                                                    

     

 

3 схема                        4 схема

     

 

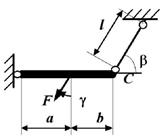
5 схема                        6 схема                    

  

 

 

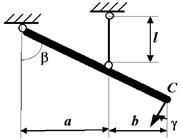
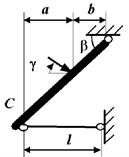
       7 схема                                8 схема                        

   

 

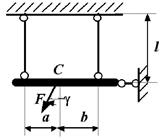
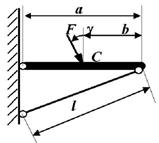
9 схема                                     10 схема

   

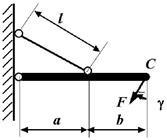
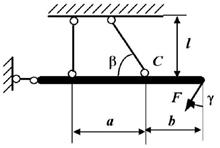
Рис. 2

 

Задача 3. Статически определимые стержневые системы растяжения-сжатия.

Плоская шарнирно-стержневая система загружена в узле силой F (на рис. 3).

Требуется:

1. Определить усилия в стержнях.

2. Подобрать размеры поперечных сечений стержней. Стержень 1 стальной, круглого поперечного сечения, стержень 2 стальной квадратного сечения.

3. Вычислить удлинения (укорочения) стержней и построить план перемещений.

4. Определить перемещение узла.

При расчете считать, что устойчивость сжатых стержней (если таковые в системе имеются) обеспечена.

Для всех вариантов принять расчетное сопротивление стали R =240 МПа,  модуль упругости   E=2∙10⁵ МПа. Остальные данные взять из табл. 3.

 

Таблица 3

 

              1 схема                              2 схема                               

    

 

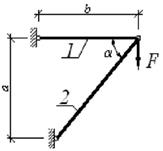
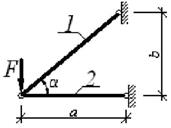
     3 схема                                     4 схема                    

      

 

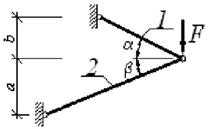
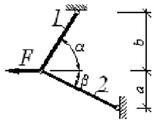
     5 схема                            6 схема                                

            

 

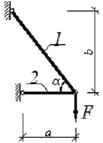
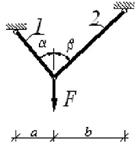
      7 схема                               8 схема                       

 

           

 

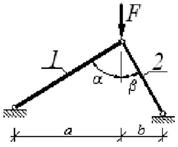
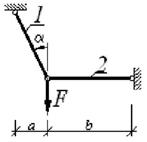
9 схема                                   10 схема

     

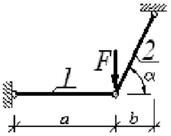
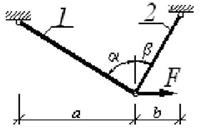
Рис. 3

 

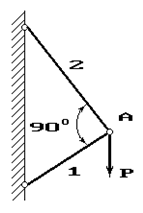
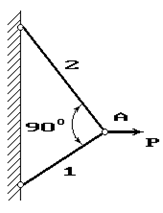
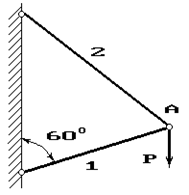
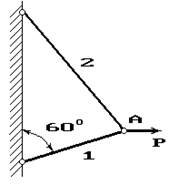
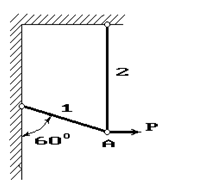
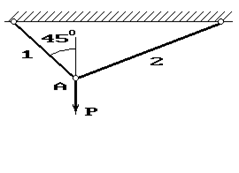
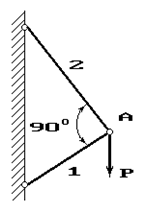
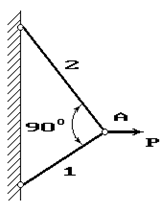
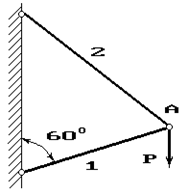
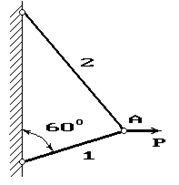
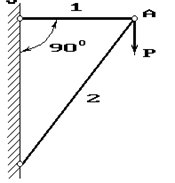
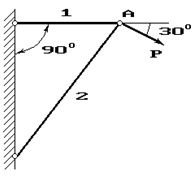
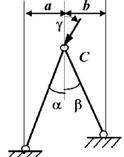
Задача 4. Расчет шарнирно-стержневого кронштейна.

Шарнирно-стержневой кронштейн изготовлен из двух стержней. Один из них стальной с допускаемым напряжением [σ]=160 МПа, другой чугунный с допускаемым напряжением при растяжении [σ_t]=40 МПа и при сжатии – [σ_c]=80 МПа. Требуется подобрать сечения стержней из условия прочности, сделав растянутый стержень стальным, а сжатый – чугунным.

Исходные данные к задаче выбираются по табл. 4 и схемам на рис. 4.

Таблица 4

 

       1 схема                                              2 схема                               

    

 

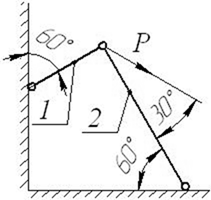
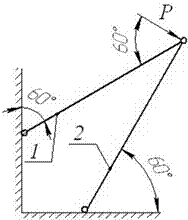
     3 схема                                            4 схема                    

      

 

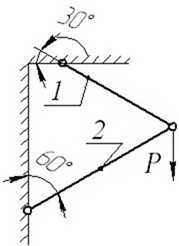
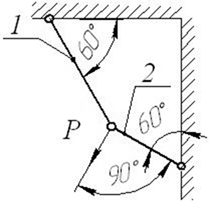
     5 схема                                           6 схема                                

            

 

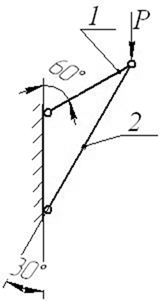
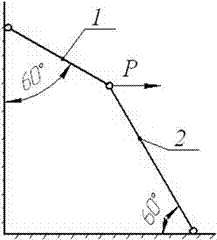
      7 схема                                              8 схема                       

           

 

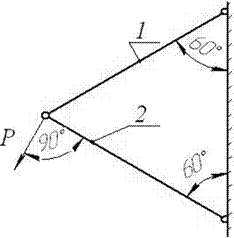
9 схема                                                     10 схема

     

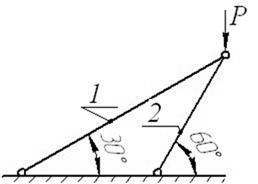
Рис. 4

 

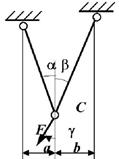
Задача 5. Расчет плоской шарнирно-стержневой системы.

Для плоской шарнирно-стержневой системы (рис. 5,а, табл.5), состоящей из трех деформируемых стержней и абсолютно жесткого тела, требуется:

1. Определить усилия в деформируемых стержнях (в долях ql);

2. Из расчета на прочность найти площади поперечных сечений стержней;

3. Учитывая, что каждый стержень фермы состоит из двух одинаковых равнополочных уголков (рис. 5,б), подобрать по ГОСТ 8509-72, соответствующий номер профиля.

Дано: материал – Сталь 5; [n] = 1,4;  l = 50 см;  q = 200 кН/м,  σ_т=280 Мпа.

Таблица 5

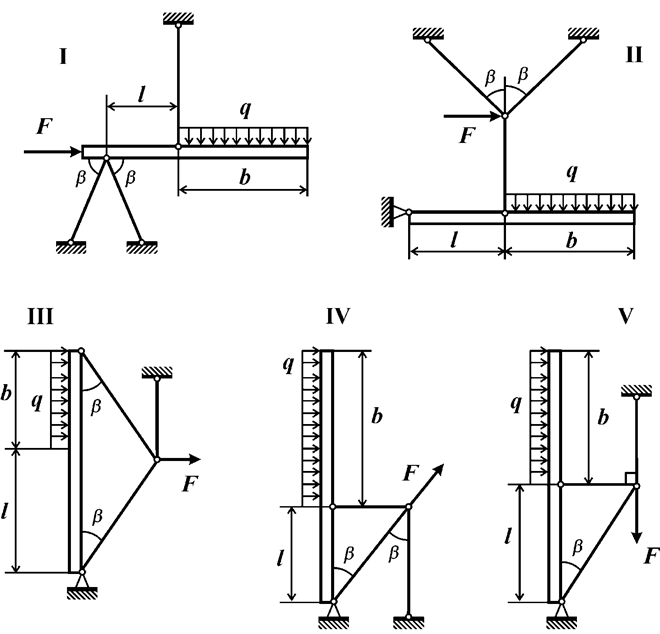
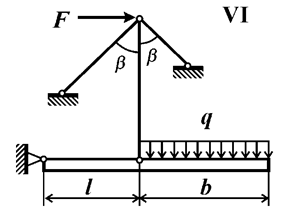
Рис.5,а

 

Рис.5,б

 

 

Примеры выполнения задач

Пример 1

Для заданной стержневой системы (рис. 6).

1. Определить усилия в стержнях;

2. Вычислить напряжения в поперечных сечениях стрежней.

3. Проверить прочность стержней, указав на сколько (в процентах) каждый из стержней недогружен или перегружен. Материал стержней сталь Ст.3, имеющая предел текучести σ_т = 240МПа, требуемый коэффициент запаса по отношению к пределу текучести [n_т] = 1,5.

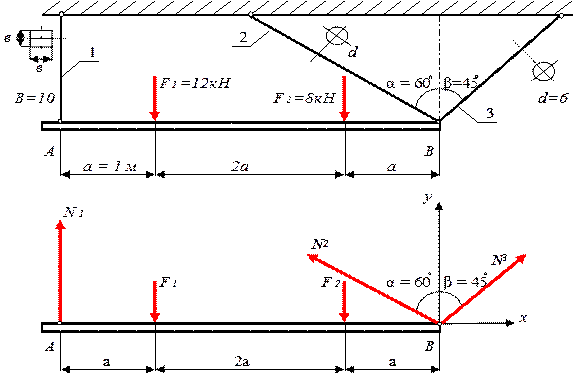
Рис.6

 

К решению подобного типа задач рекомендуется приступать, повторив раздел "статики" составление и решение уравнений равновесия плоской системы произвольно расположенных сил и иметь четкое представление об определении допускаемых напряжений и расчетах на прочность при растяжении и сжатии.

В первую очередь освобождают тело от связей и заменяют их действие на него реакциями связей, которые равны по величине продольным силам. Составляя уравнения равновесия для внешних сил, действующих на систему, и реакций связей, определяют продольные силы в поперечных сечениях бруса.

Площади поперечных сечений стержней определяют для нестандартных профилей, по формулам:

- круглое поперечное сечение , где d – диаметр стержня,

- прямоугольное сечение А = вh, где в и h стороны прямоугольного сечения.

Для профилей стандартного проката (равнополочные и неравнополочные угловые профили, швеллеры и двутавры) площади поперечных сечений определяются по таблицам ГОСТ.

Допускаемое напряжение определяется отношением предела текучести к требуемому (заданному) коэффициенту запаса [σ] = σ_т/[n_т].

 

Решение.

1) Применяем метод сечений и рассматриваем равновесие стержневой системы под действием сил F₁, F₂ и продольных сил N₁, N₂, N₃. Начало координат возьмем в точке В, направим ось х по оси балки АВ, а ось y вертикально вверх. Спроектировать все силы на ось Вх, получим

ΣF_ix = -N₂∙sinα + N₃∙sinβ = 0                                     (1)

Спроектировав все силы на ось Вх, получим

ΣF_iy = N₂∙cosα + N₃∙cosβ  + N₁ – F₁ – F₂ = 0              (2)

Взяв сумму моментов всех сил относительно точки В (в которой пересекаются две неизвестные силы N₂ и N₃), получим

ΣМ_В(F_i) = -N₁·4а + F₁·3а + F₂·а  = 0,                           (3)

откуда

Решим совместно уравнения (1) и (2). Из уравнения (1)

-N₂∙sin60⁰ + N₃∙cos45⁰ = 0

выражаем                                              (4)

поставим N₂ в уравнение (2)

 

N₃ = кН;     N₃ = 8,04 кН

Подставив N₃ в уравнение (4), получим

N₂ = 6,56 кН

 

2) Определяем площади поперечных сечений стержней

А₁ = в² = 10·10 = 100 мм²

Нормальные напряжения в поперечных сечениях стержней определяем по формуле  

 

 

3) Проверка прочности.

Определяем допускаемое напряжение  

стержень 1  на 31,25% недогружен,

стержень 2    на 45% перегружен,

стержень 3    на 77,5% перегружен.

Следовательно, надо увеличить диаметр первого стержня и уменьшить диаметры 2 и 3 стержней.

 

Пример 2

Определение размеров поперечного сечения стержней.

Емкость для хранения воды, представляет собой конструкцию АВСД, деформацией которой пренебрегаем, прикреплена к фундаменту при помощи стержней 1, 2, 3. Вес конструкции и боковое давление на нее указаны на рис. 7.

Определить из условия прочности требуемые размеры поперечных сечений стальных стержней, составленных из прокатных профилей, если для стержней, работающих на растяжение, допускаемое напряжение [σ_t] = 160 МПа; для стержней работающих на сжатие, допускаемое напряжение на сжатие [σ_с] = 100 МПа.

Рис.7

 

Решение.

При расчете стержневых конструкций надо иметь ввиду, что если стержни закреплены по концам шарнирно, то реакции стержней действуют вдоль оси стержня, т.е. имеет место одноосное нагружение.

Применяем метод сечений и рассматриваем равновесие конструкции АВСД под действием заданных нагрузок F и q и реакций стержней N₁, N₂, N₃, которые направляем от узлов. В случае, если в результате определения их величин, они окажутся отрицательными, это будет свидетельствовать о том, что их направления первоначально были выбраны неправильно и соответствующий стержень сжат. Полагая все три стержня растянутыми, направляем усилия N₁, N₂, N₃ так, как показано на (рис. 7,б).

Для равновесия конструкции АВСД в плоскости составляют три уравнения равновесия:

- сумма проекций всех сил и сил реакций связей на одну из координатных осей равна нулю:        

ΣF_iх = 0;

- сумма проекций всех сил и сил реакций связей на другую ось плоскости действия сил равна нулю:

ΣF_iy = 0;

- сумма моментов всех внешних сил и сил реакций связей относительно любой точки этой плоскости равна нулю:

Σ М_Д (F_i) = 0, где Д произвольна.

Направим координатные оси, как показано на рис. 7,б. Тогда

1. ΣF_iх = q·2 – N₂ cosα = 0

2. ΣF_iy = -N₁ – F – N₂ sinα – N₃ = 0

3.  ΣМ_Д (F_i) = q·2·1 + N₁·4 + F·2 = 0

Отсюда находим из (3) уравнения

N₁ = -141 кН,  т.е. стержень 1 – сжат

из уравнения (1)

где : т.к.

N₂ = 45 кН,  т.е. стержень 2 – растянут.

Подставляя N₁ и N₂ в уравнение (2), определим N₃;

+141 – 300 - 45·0,6 - N₃ = 0

N₃ = +141 – 300 – 27,0 = -186 кН

N₃ = -186 кН  т.е. стержень 3 – сжат.

Определяем площади поперечных сечений стержней. Из условия прочности стержня 1.

Определяем необходимую площадь его поперечного сечения

Так как стержень 1 состоит из двух швеллеров, то площадь поперечного сечения одного швеллера равна

из таблиц Сортамента по ГОСТ 8240-89 ближайший номер швеллера № 6,5, у которого А= 7,51 см².

Выбираем для стержня 1 два швеллера № 6,5 А₁= 7,51 см².

Из условия прочности стержня 2

Определяем необходимую площадь его поперечного сечения

Так как стержень 2 состоит из двух равнополочных уголков, то

По ГОСТ 8509-86 ближайший уголок № 2  20х20х4  А = 1,46 см².

Выбираем для стержня 2 два равнополочных уголка №2 20х20х4 А=1,46 см².

Из условия прочности стержня 3

Определяем необходимую площадь его поперечного сечения

так как стержень 3 состоит из двух швеллеров, то

по ГОСТ 8240-89 ближайший швеллер № 8  А= 8,98 см²

Выбираем для стержня 3 два швеллера № 8  А= 8,98 см²

 

 

Пример 3

Стержень ВС кронштейна (рис. 8,а) составлен из двух стальных равнополочных уголков 50х50х5, а стержень АВ – из двух стальных швеллеров №8.

Требуется определить допускаемые значения силы F, действующей на стальной кронштейн в точке В, если допускаемые напряжения для материала на растяжение [σ_t] = 160 МН/м², [σ_с] = 100 МН/м².

Рис.8

 

Решение.

Вырежем мысленно узел В (рис.8,б). Обозначим продольную силу в стержне ВС через N₁, а в стержне АВ – N₂ и рассмотрим условие равновесия узла В.

Для данной системы сходящихся сил можно составить два уравнения равновесия:

ΣF_ix = N₁ + N₂·cosα= 0

ΣF_iy = -F - N₂·sinα= 0

Из 2^го уравнения получаем

Следовательно, стержень АВ сжат силой N₂.

Из 1^го уравнения  т.е. элемент ВС растянут силой N₁.

Из треугольника АВС определим значение sinα и ctgα. По теореме Пифагора

АВ²=АС²+ВС²  отсюда,

Тогда                     

Определяем значения N₁ и N₂, выраженные через силу F.

Из условия прочности  максимальные продольные усилия, которые можно допустить в поперечных сечения стержней равны:

[N₁] = [σ_р]·A₁ = 160·480·2 = 921600 Н, где A₁ = 4,8·2 = 9,6 см² для двух уголков 50х50х5.

[N₂] = [σ_с]·A₂ = 100·898 = 89800 Н, где A₂ = 8,98 см² для швеллера № 8.

Следовательно, исходя из расчета прочности кронштейна по слабому звену, допустимая нагрузка из соотношения N₂ = -1,67F равна

Ответ: [F] =53,8 кН.

 

 

Пример 4

Шарнирно-стержневой кронштейн изготовлен из двух стержней (рис. 9). Один из них стальной с допускаемым напряжением [σ] = 160 Мпа , другой чугунный с допускаемым напряжением при растяжении [σ_t] = 40 Мпа и при сжатии – [σ_c] = 80 Мпа. Требуется подобрать сечения стержней из условия их прочности, сделав растянутый стержень стальным, а сжатый – чугунным.

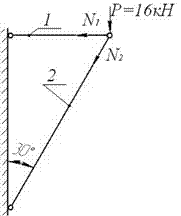
Рис.9

Решение.

Полагая стержни растянутыми, изобразим силы, приложенные к узлу В.

Уравнения равновесия системы сходящихся сил

Решение уравнений:

Отрицательное значение силы N₂ говорит о том, что стержень 2 сжат и его следует по условию задачи сделать чугунным с допускаемым напряжением [σ_c] = 80 Мпа.

По условию прочности

требуемая площадь поперечного сечения первого стержня, изготовленного из стали,

Площадь сечения второго стержня

 

Онлайн-калькулятор "Расчет прочности при растяжении-сжатии"

 

---