Главная

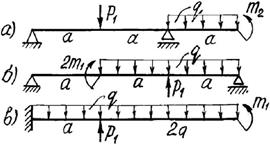
Задача 1. Подбор сечений консольных и двухопорных балок, работающих на поперечный изгиб

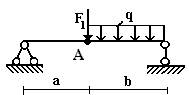
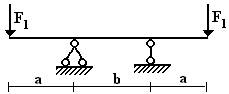
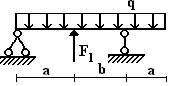
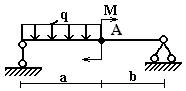
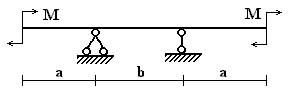
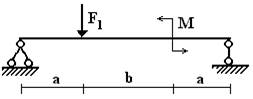
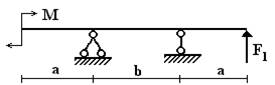
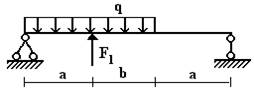
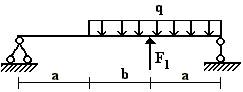
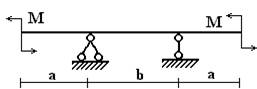
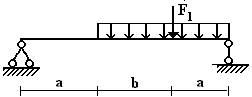
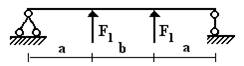
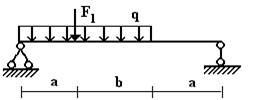
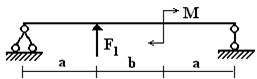
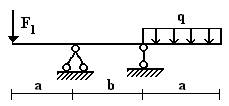
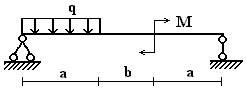
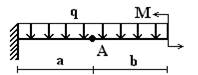
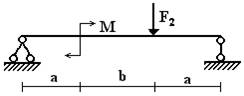
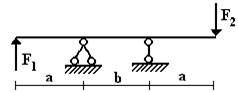
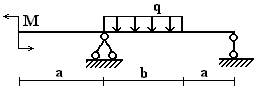
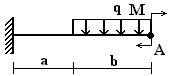
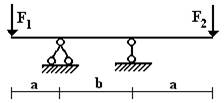
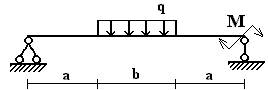
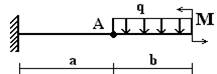
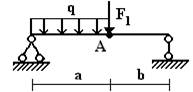
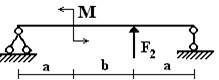
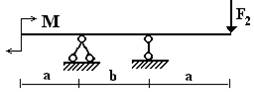
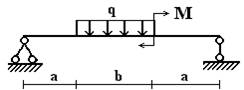
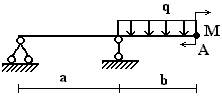
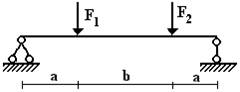
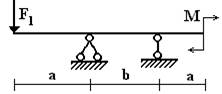
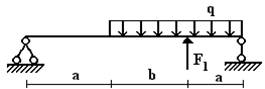
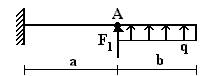
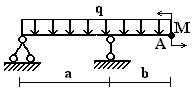
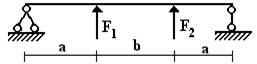
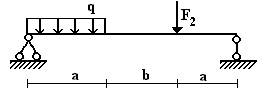
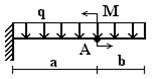
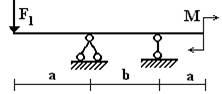
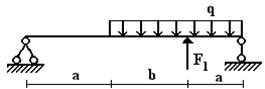
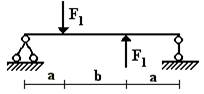
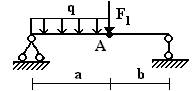
Для балок, изображенных на схемах 1 – 5 (рис.1), требуется:

1) простроить эпюры внутренних усилий;

2) указать положение опасного сечения.

3) для деревянной балки, изображенной на схеме 1, подобрать размеры квадратного поперечного сечения из условия прочности, если [σ] = 16 МПа;

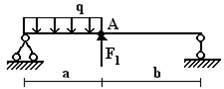
4) для стальной двутавровой балки, изображенной на схеме 2, подобрать номер прокатного профиля из условия прочности.

Данные для схем 1 – 5 взять из табл.1.

Таблица 1

Номер cтроки	Схема по рис.1	F1, см^2	а, м	b, м	М, кНм	q, кН/м
01	1	12	1	2	24	5
02	2	10	2	2	16	4
03	3	12	3	2	12	6
04	4	6	2	3	18	2
05	5	8	1	3	20	4
06	6	10	3	1	12	2
07	7	6	2	2	12	3
08	8	8	1	2	12	6
09	9	6	2	1	16	5
10	10	12	1	3	10	6
11	11	11	1	2	12	6
12	12	12	3	3	18	2
13	13	10	2	3	20	4
14	14	12	1	1	12	2
15	15	6	2	2	12	3
16	16	8	1	2	12	6
17	17	10	2	1	18	5
18	18	6	3	2	20	6
19	19	8	2	2	12	2
20	20	6	1	3	12	4
21	21	12	3	3	12	2
22	22	12	2	1	16	3
23	23	13	1	2	10	6
24	24	14	1	2	12	5
25	25	12	3	1	18	6
26	26	10	2	3	20	6
27	27	12	1	2	12	2
28	28	6	2	3	24	4
29	29	8	1	3	16	2
30	30	10	2	1	12	3
31	31	6	3	2	18	6
32	32	8	2	2	20	5
33	33	6	1	1	12	6
34	34	12	3	3	12	2
35	35	11	2	2	16	4
36	36	12	3	3	12	2
	а	г	в	б	г	а

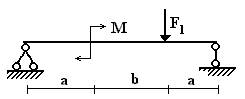
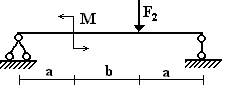
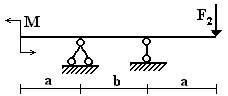
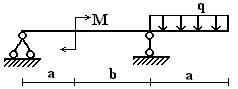
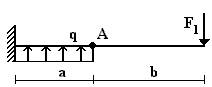
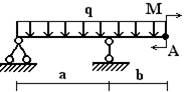
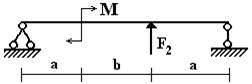
Вариант 1.

1 схема 2 схема 3 схема

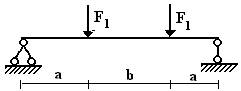
4 схема 5 схема

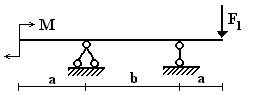
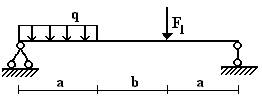
Вариант 2.

1 схема 2 схема 3 схема

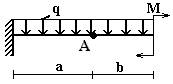
4 схема 5 схема

Вариант 3.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 4.

1 схема 2 схема 3 схема

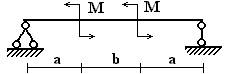
4 схема 5 схема

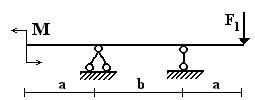
Вариант 5.

1 схема 2 схема 3 схема

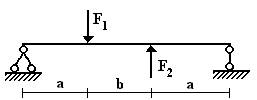
4 схема 5 схема

Вариант 6.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 7.

1 схема 2 схема 3 схема

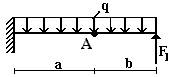
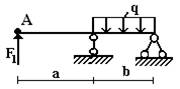
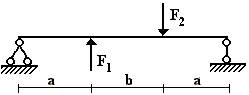
4 схема 5 схема

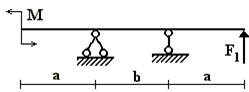
Вариант 8.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 9.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 10.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 11.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 12.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 13.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 14.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 15.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 16.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 17.

1 схема 2 схема 3 схема

4 схема 5 схема

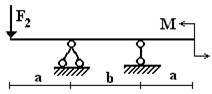
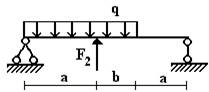
Вариант 18.

1 схема 2 схема 3 схема

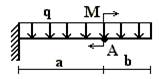
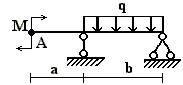
4 схема 5 схема

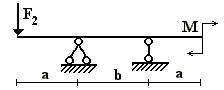
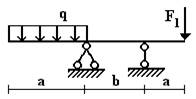
Вариант 19.

1 схема 2 схема 3 схема

4 схема 5 схема

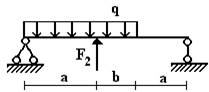
Вариант 20.

1 схема 2 схема 3 схема

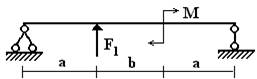
4 схема 5 схема

Вариант 21.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 22.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 23.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 24.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 25.

1 схема 2 схема 3 схема

4 схема 5 схема

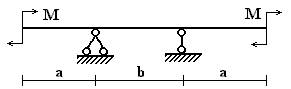
Вариант 26.

1 схема 2 схема 3 схема

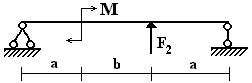
4 схема 5 схема

Вариант 27.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 28.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 29.

1 схема 2 схема 3 схема

4 схема 5 схема

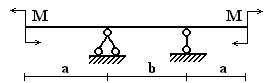
Вариант 30.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 31.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 32.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 33.

1 схема 2 схема 3 схема

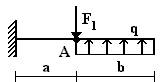
4 схема 5 схема

Вариант 34.

1 схема 2 схема 3 схема

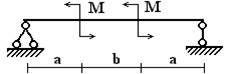
4 схема 5 схема

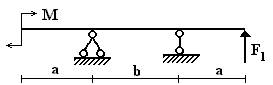
Вариант 35.

1 схема 2 схема 3 схема

4 схема 5 схема

Вариант 36.

1 схема 2 схема 3 схема

4 схема 5 схема

Рис.1

Задача 2. Подбор сечений консольных и двухопорных балок, работающих на поперечный изгиб

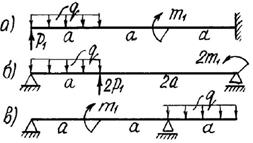
Для заданных схем балок, изображенных на схемах а) и б) (рис.2), требуется:

1) простроить эпюры внутренних усилий Q и изгибающего момента М.

2) подобрать поперечное сечение для схемы а) круглое [σ] = 10 МПа; б) двутавровое [σ] = 150 МПа.

Данные для схем а) и б) взять из табл.2.

Таблица 2

Номер cтроки	Схема по рис.2	а, м	q1=q3, кН/м	q2, кН/м	F1, кН	F2, кН	F3, кН	М1, кНм	М2, кНм	М3, кНм
01	1	2	5	30	10	35	10	10	35	10
02	2	0,8	10	25	15	30	20	15	30	20
03	3	1	15	20	20	25	30	20	25	30
04	4	1,2	20	15	25	20	40	25	20	40
05	5	1,4	25	10	30	15	10	30	15	10
06	6	1,6	30	5	35	10	20	35	10	20
07	7	1,8	5	30	40	5	30	40	5	30
08	8	2	15	35	15	30	20	15	30	20
09	9	2	20	25	20	25	30	20	25	30
10	10	0,8	25	20	25	20	40	25	20	40
11	11	1	30	15	30	15	10	30	15	10
12	12	1,2	5	10	15	10	20	35	10	20
13	13	1,4	20	25	20	5	30	40	30	30
14	14	1,6	10	20	25	20	30	20	25	30
15	15	1,8	15	15	30	15	40	25	20	40
16	16	1	20	10	35	10	10	30	15	10
17	17	1,2	25	5	40	5	20	35	10	20
18	18	1,4	30	30	15	30	30	40	5	30
19	19	1,6	5	35	20	25	20	15	30	20
20	20	1,8	15	25	25	20	30	20	25	30
21	21	2	20	20	30	15	40	25	20	40
22	22	2	25	15	25	10	10	30	15	10
23	23	0,8	30	10	30	5	20	35	10	20
24	24	1	5	35	35	25	20	40	20	30
25	25	1,2	20	25	40	20	30	20	15	20
26	26	1,4	20	20	15	15	40	25	10	30
27	27	1,4	20	15	20	10	10	30	30	40
28	28	1,6	25	10	25	5	20	35	25	10
29	29	1,8	30	25	30	20	30	40	20	20
30	30	1	5	20	15	15	30	15	15	30
31	31	1,2	20	15	20	10	40	20	10	30
32	32	1,4	10	10	25	5	10	25	5	40
33	33	1,6	15	5	30	30	20	30	30	10
34	34	1,8	20	30	35	25	30	35	30	20
35	35	1,8	25	20	30	15	20	40	25	30
36	36	1	15	30	15	10	40	15	20	10
	в	б	б	а	в	в	г	а	г	в

1 схема 2 схема

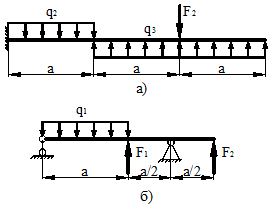
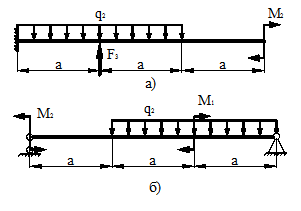
3 схема 4 схема

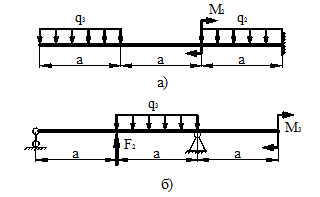
5 схема 6 схема

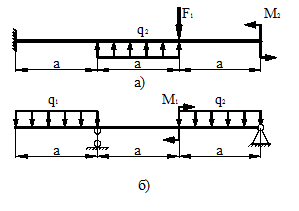
7 схема 8 схема

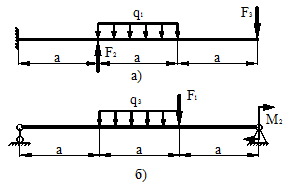
9 схема 10 схема

11 схема 12 схема

13 схема 14 схема

15 схема 16 схема

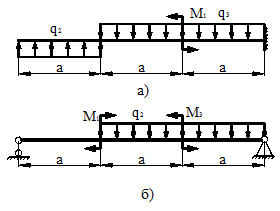
17 схема 18 схема

19 схема 20 схема

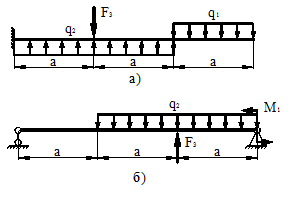
21 схема 22 схема

23 схема 24 схема

25 схема 26 схема

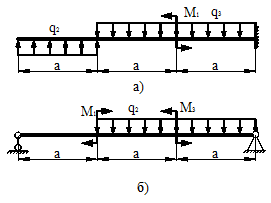
27 схема 28 схема

29 схема 30 схема

31 схема 32 схема

33 схема 34 схема

35 схема 36 схема

Рис.2

Задача 3. Подбор сечений двухопорных балок, работающих на поперечный изгиб

Для заданной двухопорной балки при указанных на схеме нагрузках и размерах требуется:

1. Определить опорные реакции.

2. Построить аналитически эпюры поперечных сил и изгибающих моментов.

3. Установить опасные сечения для нормальных и для касательных напряжений.

4. Подобрать двутавровое сечение, приняв [σ] = 160 МПа, и выполнить его проверку по нормальным напряжениям.

5. Выполнить проверку по касательным напряжениям, приняв [τ] = 96 МПа.

6. Построить для соответствующих опасных сечений эпюры нормальных и касательных напряжений.

Примечание: Данные для решения задачи взять в табл.3 и на рис. 3.

Таблица 3

Номер строки	Схема по рис.3	Параметры	Числовые значения вариантов
			1	2	3	4	5	6	7	8	9	10
01	1	М, кН	20	24	30	28	23	40	36	33	35	25
02	2	F, кН	30	20	40	50	25	15	28	23	35	33
03	3	q, кН/м	50	60	80	40	70	30	50	25	40	60
04	4	l, м	1,0	1,5	2,0	1,0	1,5	1,0	0,5	1,0	1,5	1,0
05	5	М, кН	25	40	35	45	30	37	23	50	45	28
06	6	F, кН	15	20	35	22	28	30	40	36	24	45
07	7	q, кН/м	20	40	30	25	25	30	40	35	50	35
08	8	l , м	1,5	1,2	1,0	0,5	0,5	1,0	1,5	1,0	1,2	0,5
09	9	М, кН	30	20	15	18	28	25	18	25	22	32
10	10	F, кН	20	35	25	28	40	30	26	30	24	45
11	11	q, кН/м	50	40	60	80	90	60	50	40	50	60
12	12	l, м	1,0	1,5	1,0	1,0	0,6	0,5	1,0	2,0	1,0	1,5
13	13	М, кН	20	24	30	28	23	40	36	33	35	25
14	14	F, кН	30	20	40	50	25	15	28	23	35	33
15	15	q, кН/м	50	60	80	40	70	30	50	25	40	60
16	16	l, м	1,0	1,5	2,0	1,0	1,5	1,0	0,5	1,0	1,5	1,0
17	17	М, кН	20	24	30	28	23	40	36	33	35	25
18	18	F, кН	30	20	40	50	25	15	28	23	35	33
19	19	q, кН/м	50	60	80	40	70	30	50	25	40	60
20	20	l, м	1,0	1,5	2,0	1,0	1,5	1,0	0,5	1,0	1,5	1,0
21	21	М, кН	20	24	30	28	23	40	36	33	35	25
22	22	F, кН	30	20	40	50	25	15	28	23	35	33
23	23	q, кН/м	50	60	80	40	70	30	50	25	40	60
24	24	l, м	1,0	1,5	2,0	1,0	1,5	1,0	0,5	1,0	1,5	1,0
25	25	М, кН	20	24	30	28	23	40	36	33	35	25
26	26	F, кН	30	20	40	50	25	15	28	23	35	33
27	27	q, кН/м	50	60	80	40	70	30	50	25	40	60
28	28	l, м	1,0	1,5	2,0	1,0	1,5	1,0	0,5	1,0	1,5	1,0
29	29	М, кН	20	24	30	28	23	40	36	33	35	25
30	30	F, кН	30	20	40	50	25	15	28	23	35	33
	в		а	б	в	г	а	б	в	г	а	б

1 схема 2 схема

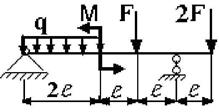
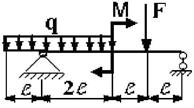
3 схема 4 схема

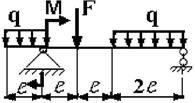
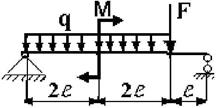
5 схема 6 схема

7 схема 8 схема

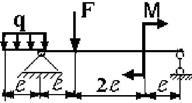
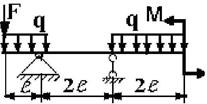
9 схема 10 схема

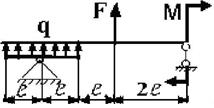
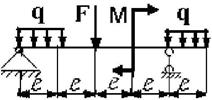
11 схема 12 схема

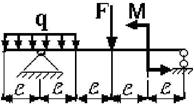
13 схема 14 схема

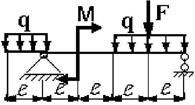
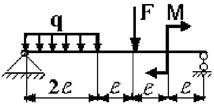
15 схема 16 схема

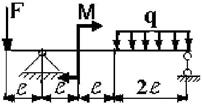
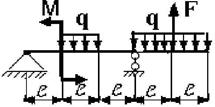
17 схема 18 схема

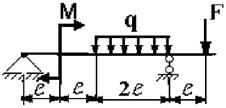
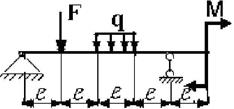
19 схема 20 схема

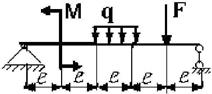
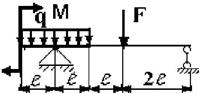
21 схема 22 схема

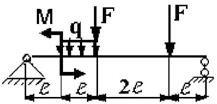
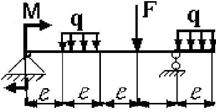
23 схема 24 схема

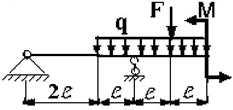
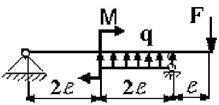
25 схема 26 схема

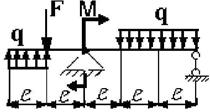
27 схема 28 схема

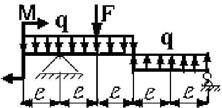
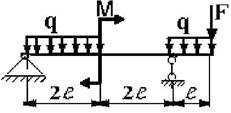
29 схема 30 схема

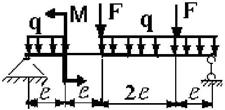
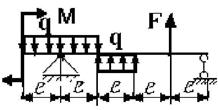
Рис. 3

Задача 4. Подбор сечений консольных балок, работающих на поперечный изгиб

Для заданной консольной балки при указанных на схеме нагрузках и размерах требуется:

1. Определить опорные реакции.

2. Построить аналитически эпюры поперечных сил и изгибающих моментов.

3. Установить опасное сечение балки по нормальным напряжениям.

4. Подобрать прямоугольное сечение при соотношении сторон b/h = 0,5, приняв [σ] = 8,3 МПа (сосна).

5. Построить эпюру нормальных напряжений для опасного сечения.

6. Рассчитать для опасного сечения балки величину нормальных напряжений в слое, расположенном на расстоянии a = 6 см от кромки сечения и показать эти напряжения на эпюре.

Примечание: Данные для решения задачи взять в табл. 4, на рис. 4.

Таблица 4

Номер строки	Схема по рис.4	Параметры	Числовые значения вариантов
			1	2	3	4	5	6	7	8	9	10
01	1	М, кН	20	12	20	12	18	13	22	15	12	14
02	2	F, кН	15	40	32	20	28	33	30	40	25	26
03	3	q, кН	20	10	5	8	18	15	22	19	16	14
04	4	l, м	1,0	1,5	2,0	2,5	2,0	1,0	0,5	1,0	1,5	2,0
05	5	М, кН	28	26	30	25	16	20	10	24	17	27
06	6	F, кН	25	15	30	26	22	16	25	33	18	20
07	7	q, кН	10	12	7	16	12	17	9	8	6	15
08	8	l, м	1,5	2,0	1,0	0,5	1,0	2,0	2,0	1,0	1,0	2,0
09	9	М, кН	20	10	15	18	14	23	17	24	16	27
10	10	F, кН	10	8	20	15	22	12	15	10	14	15
11	11	q, кН	22	8	10	12	14	18	10	12	8	14
12	12	l, м	1,0	1,5	3,0	2,0	1,0	0,5	1,5	2,5	2,0	1,0
13	13	М, кН	20	12	20	12	18	13	22	15	12	14
14	14	F, кН	15	40	32	20	28	33	30	40	25	26
15	15	q, кН	20	10	5	8	18	15	22	19	16	14
16	16	l, м	1,0	1,5	2,0	2,5	2,0	1,0	0,5	1,0	1,5	2,0
17	17	М, кН	20	12	20	12	18	13	22	15	12	14
18	18	F, кН	15	40	32	20	28	33	30	40	25	26
19	19	q, кН	20	10	5	8	18	15	22	19	16	14
20	20	l, м	1,0	1,5	2,0	2,5	2,0	1,0	0,5	1,0	1,5	2,0
21	21	М, кН	20	12	20	12	18	13	22	15	12	14
22	22	F, кН	15	40	32	20	28	33	30	40	25	26
23	23	q, кН	20	10	5	8	18	15	22	19	16	14
24	24	l, м	1,0	1,5	2,0	2,5	2,0	1,0	0,5	1,0	1,5	2,0
25	25	М, кН	20	12	20	12	18	13	22	15	12	14
26	26	F, кН	15	40	32	20	28	33	30	40	25	26
27	27	q, кН	20	10	5	8	18	15	22	19	16	14
28	28	l, м	1,0	1,5	2,0	2,5	2,0	1,0	0,5	1,0	1,5	2,0
29	29	М, кН	20	12	20	12	18	13	22	15	12	14
30	30	F, кН	15	40	32	20	28	33	30	40	25	26
	г		в	а	г	б	г	а	б	в	а	г

1 схема 2 схема

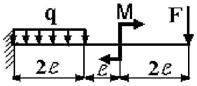
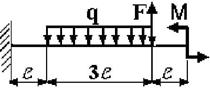
3 схема 4 схема

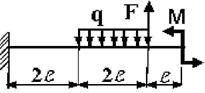
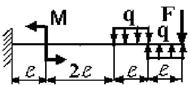
5 схема 6 схема

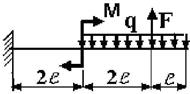
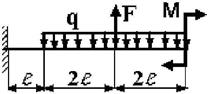
7 схема 8 схема

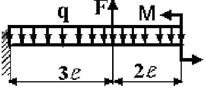
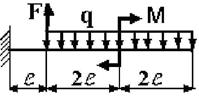
9 схема 10 схема

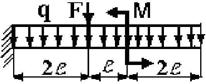
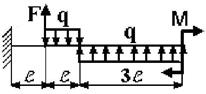
11 схема 12 схема

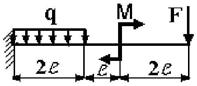
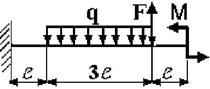
13 схема 14 схема

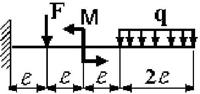
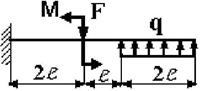
15 схема 16 схема

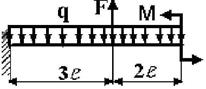
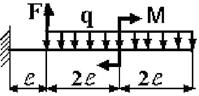
17 схема 18 схема

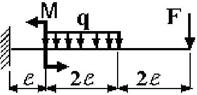
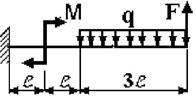
19 схема 20 схема

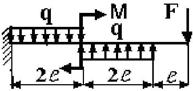
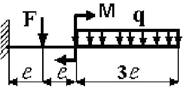
21 схема 22 схема

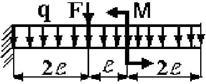
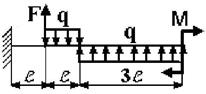
23 схема 24 схема

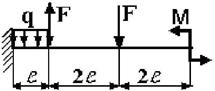
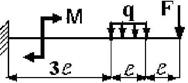
25 схема 26 схема

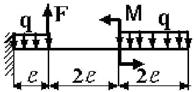
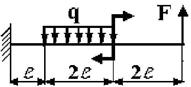
27 схема 28 схема

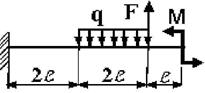
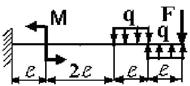
29 схема 30 схема

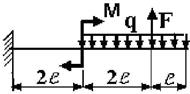
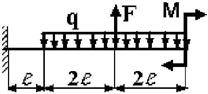
Рис. 4

Задача 5. Подбор сечений консольных и двухопорных балок, работающих на поперечный изгиб

Для заданных схем балок требуется:

Построить эпюры поперечных сил и изгибающих моментов; подобрать поперечные сечения балок по следующим вариантам:

а) для стальной балки (рис.5.1, а) - двутавровое; прямоугольное высотой h и основанием b при соотношении сторон h/b=2; круглое - диаметром d;

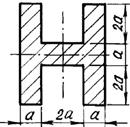
б) для чугунной балки (рис.5.1, б) - форму сечения выбрать по рис.5.2, определить размеры сечения из условия прочности по допускаемым напряжениям;

в) для стальной балки (рис.5.1, в) - сечение, состоящее из двух швеллеров.

Для стальной двутавровой балки (вариант а) и чугунной балки (вариант б) построить эпюры распределения нормальных напряжений по высоте сечения.

Числовые данные берутся из табл.5, расчетные схемы – на рис.5.1.

Таблица 5

Номер строки	Схема по рис. 5.1, 5.2	Сила		Момент		Длина участка а,м	Интенсивность распределенной нагрузки q, кН/м	Допускаемое напряжение, [σ], МПа
		P1, кН	P2, кН	m1, кНм	m2, кНм			Сталь	Чугун
									[σ]с	[σ]р
01	1	40	90	10	10	1	10	200	600	120
02	2	45	80	12	10	1,5	15	160	700	150
03	3	50	85	15	14	2	20	180	500	100
04	4	35	70	12	12	1	10	250	800	150
05	5	50	80	10	15	2	10	160	600	120
06	6	60	70	10	12	1	15	180	700	150
07	7	45	60	12	10	1,5	20	180	500	100
08	8	35	65	10	10	1	10	160	800	150
09	9	40	75	13	10	1	10	160	650	130
10	10	30	90	18	12	2	15	220	750	200
	з	ж	а	б	в	г	ж	е	з	з

1 схема 2 схема

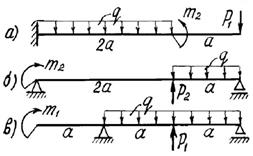
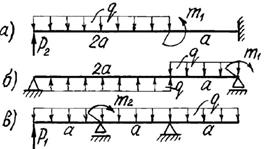
3 схема 4 схема

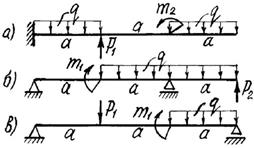
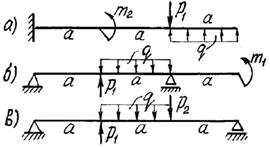
5 схема 6 схема

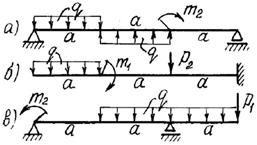
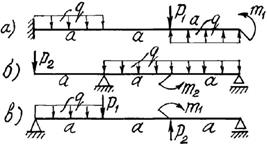
7 схема 8 схема

9 схема 10 схема

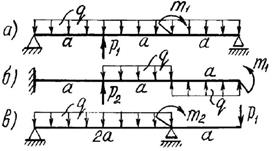
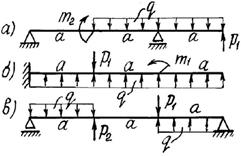
Рис. 5.1

1 схема 2 схема 3 схема 4 схема 5 схема

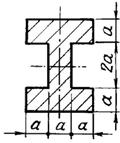
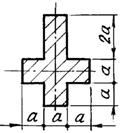
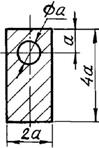
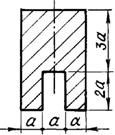
6 схема 7 схема 8 схема 9 схема 10 схема

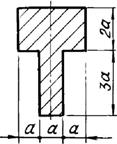
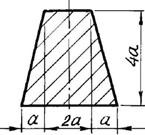
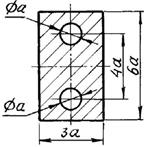
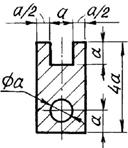
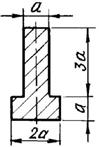
Рис. 5.2

Задача 6. Проверка прочности и подбор сечений консольных и двухопорных балок, работающих на поперечный изгиб

Даны две схемы стальных балок (рис. 6)

Требуется:

Для схемы «а»:

1. Построить эпюры поперечной силы Q и изгибающего момента M.

2. Проверить прочность по нормальным напряжениям в балке сложного поперечного сечения.

3. Вычислить коэффициент использования прочности стали балки.

4. Определить прогиб конца консоли аналитическим методом, составляя и интегрируя дифференциальные уравнения изогнутой оси балки.

Для схемы «б»:

1. Построить эпюры поперечной силы Q и изгибающего момента M.

2. Подобрать сечения следующей формы: прямоугольное (h/b = k); круглое; кольцевое (α= d/D); состоящее из двух швеллеров; двутавровое.

3. Оценить эффективность формы сечения.

Для всех вариантов принять расчетное сопротивление стали R =240 МПа, модуль упругости (модуль Юнга) E=2∙10⁵ МПа. Остальные данные взять из табл. 6

Таблица 6

Номер строки	Схема по рис.6	а1, м	а2, м	q, кН/м	F, кН	М, кНм	k	α
01	1	1,0	2,0	10	25	10	1,5	0,7
02	2	1,2	1,8	12	24	15	2,0	0,8
03	3	1,4	1,6	14	22	20	2,5	0,9
04	4	1,6	1,4	16	20	25	3,0	0,8
05	5	1,2	1,8	18	18	30	2,5	0,7
06	1	2,0	1,0	20	16	35	2,0	0,8
07	2	1,8	1,2	22	15	30	1,5	0,7
08	3	1,6	1,4	24	14	25	2,0	0,9
09	4	1,4	1,6	26	12	20	2,5	0,8
10	5	1,2	1,8	28	10	15	3,0	0,9
	е	а	б	в	г	д	е	б

1 схема

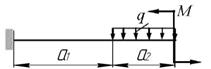
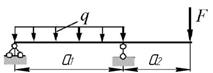
а) б)

2 схема

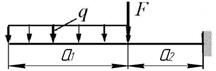
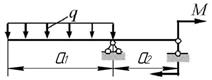
а) б)

3 схема

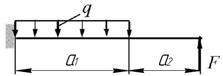
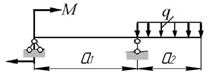
а) б)

4 схема

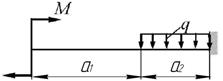
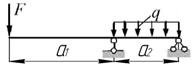
а) б)

5 схема

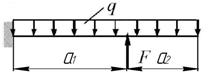
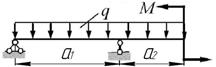
а) б)

Рис.6

Задача 7. Подбор сечения и определение перемещений двутавровой балки при плоском изгибе из условия прочности и жесткости

Для заданной балки при указанных на схеме нагрузках и размерах балки, форме поперечного сечения требуется:

1. разбить балку на участки, обозначив длину каждого из них;

2. определить реакции опор;

3. записать аналитические выражения для внутренних усилий на каждом участке;

4. построить эпюры внутренних усилий в выбранном масштабе;

5. по эпюре определить максимальный по модулю изгибающий момент и назначить размеры поперечного сечения, используя условие прочности по нормальным напряжениям;

6. записать уравнения метода начальных параметров для моментов, углов поворота сечений и прогибов;

7. построить эпюры углов поворота и прогибов;

8. проверить правильность построения эпюр по дифференциальным зависимостям между моментами, углами поворота и прогибами;

9. найти максимальный по модулю прогиб и назначить размеры поперечного сечения по условию жесткости;

10. назначить окончательные размеры поперечного сечения по условиям прочности и жесткости.

Примечание: Данные для решения задачи взять в табл. 7 и на рис. 7.

Дополнительно для всех вариантов принять: форму поперечного сечения балки – стандартный двутавровый профиль; расчетное сопротивление стали R = 200 МПа; нормативный прогиб [v] = a/300; модуль упругости стали E = 2∙10⁵ МПа.

Таблица 7

Номер cтроки	Схема по рис.7	a, м	F, кН	М, кНм	q, кН/м
01	1	4,0	10	30	3
02	2	3,0	14	12	5
03	3	2,0	12	24	4
04	4	2,5	16	18	8
05	5	3,5	20	20	10
06	6	4,0	18	22	7
07	7	3,0	10	16	6
08	8	2,0	14	26	9
09	9	3,5	12	28	3
10	10	4,0	16	14	5
11	11	2,0	20	22	4
12	12	2,5	18	30	8
13	13	3,5	10	24	10
14	14	4,0	14	16	7
15	15	2,5	12	20	6
16	16	2,0	16	28	9
17	17	3,5	20	14	3
18	18	3,0	18	18	5
19	19	4,0	10	30	4
20	20	3,0	14	12	6
21	21	2,0	12	24	9
22	22	2,5	16	30	3
23	23	3,5	20	12	5
24	24	4,0	18	24	4
25	25	3,0	10	18	8
26	26	2,0	14	20	10
27	27	3,5	12	22	7
28	28	4,0	16	16	6
29	29	2,0	20	26	9
30	30	2,5	18	28	3
31	31	3,5	10	14	5
32	32	4,0	14	22	4
33	33	2,5	12	30	6
34	34	2,0	16	24	9
35	35	3,5	20	16	3
36	36	3,0	18	20	5
	б	а	в	а	г

Рис.7

Задача 8. Подбор различных сечений стальной балки при плоском изгибе из условия прочности

Для балки (рис. 8), нагруженной сосредоточенными силами, моментами и равномерно распределенными нагрузками, построить эпюры внутренних силовых факторов - поперечной силы Q_у и изгибающего момента М_х. Из условия прочности по нормальным напряжениям подобрать для балки двутавровое, прямоугольное (h = 2b), круглое, кольцевое (α= d/D = 0,8) сечения. Сравнить веса балок с подобранными поперечными сечениями.

Данные для решения задачи взять в табл. 8 и на рис. 8. Принять [σ] = 160 МПа.

Рекомендуемый порядок выполнения задачи

1. Составить расчётную схему балки, нагруженной внешними силами.

2. Определить реакции опор.

3. Определить внутренние усилия Q и M по участкам и построить их эпюру.

4. Выполнить расчёт прочности балки по допускаемому нормальному напряжению, определив опасное сечение балки по эпюре изгибающих моментов для двутавра.

5. Определить безопасные размеры поперечных сечений для заданных вариантов профилей.

6. Выбрать наиболее экономичный вариант сечения балки (по весу).

7. Сделать выводы.

Таблица 8

Номер cтроки	Схема по рис.8	a, м	b, м	c, м	F, кН	М, кНм	q, кН/м
01	1	0,5	0,2	0,5	-80	20	10
02	2	0,7	0,1	0,7	60	-30	12
03	3	0,6	0,5	0,6	20	40	-14
04	4	0,3	0,6	0,3	-50	25	10
05	5	0,2	0,3	0,2	60	-32	-18
06	6	0,1	0,4	0,5	-70	26	20
07	7	0,5	0,2	0,7	80	-48	30
08	8	0,6	0,1	0,6	50	19	-24
09	9	0,3	0,2	0,2	-60	26	32
10	10	0,4	0,1	0,3	70	-35	15
11	1	0,5	0,2	0,5	-80	20	10
12	2	0,7	0,1	0,7	60	-30	12
13	3	0,6	0,5	0,6	20	40	-14
14	4	0,3	0,6	0,3	-50	25	10
15	5	0,2	0,3	0,2	60	-32	-18
16	6	0,1	0,4	0,5	-70	26	20
17	7	0,5	0,2	0,7	80	-48	30
18	8	0,6	0,1	0,6	50	19	-24
19	9	0,3	0,2	0,2	-60	26	32
20	10	0,4	0,1	0,3	70	-35	15
21	1	0,5	0,2	0,5	-80	20	10
22	2	0,7	0,1	0,7	60	-30	12
23	3	0,6	0,5	0,6	20	40	-14
24	4	0,3	0,6	0,3	-50	25	10
25	5	0,2	0,3	0,2	60	-32	-18
26	6	0,1	0,4	0,5	-70	26	20
27	7	0,5	0,2	0,7	80	-48	30
28	8	0,6	0,1	0,6	50	19	-24
29	9	0,3	0,2	0,2	-60	26	32
30	10	0,4	0,1	0,3	70	-35	15
31	1	0,5	0,2	0,5	-80	20	10
32	2	0,7	0,1	0,7	60	-30	12
33	3	0,6	0,5	0,6	20	40	-14
34	4	0,3	0,6	0,3	-50	25	10
35	5	0,2	0,3	0,2	60	-32	-18
36	6	0,1	0,4	0,5	-70	26	20
	б	а	г	б	в	а	г

Рис.8

Задача 9. Подбор различных сечений стальной балки при плоском изгибе из условия прочности

Для заданной консоли (рис.9, схема «а») и двухопорной балки (рис.9, схема «б») требуется:

1. Построить, соблюдая масштаб, эпюры поперечной силы и изгибающего момента, указав на их характерные ординаты.

2. Подобрать из условия прочности двутавровое сечение балки и определить требуемые размеры прямоугольного сечения при соотношении сторон прямоугольника h=2b. Допускаемое напряжение [σ]=160 МПа.

3. Сравнить площади двутаврового и прямоугольного сечений.

Данные для решения задачи взять в табл. 9 и на рис. 9.

Таблица 9

Номер cтроки	Схема по рис.9	l, м	P, кН	m, кНм	q, кН/м
01	1	0,5	-80	20	10
02	2	0,7	60	-30	12
03	3	0,6	20	40	-14
04	4	0,3	-50	25	10
05	5	0,2	60	-32	-18
06	6	0,1	-70	26	20
07	7	0,5	80	-48	30
08	8	0,6	50	19	-24
09	9	0,3	-60	26	32
10	10	0,4	70	-35	15
11	11	0,5	-80	20	10
12	12	0,7	60	-30	12
13	13	0,6	20	40	-14
14	14	0,3	-50	25	10
15	15	0,2	60	-32	-18
16	16	0,1	-70	26	20
17	17	0,5	80	-48	30
18	18	0,6	50	19	-24
19	19	0,3	-60	26	32
20	20	0,4	70	-35	15
21	1	0,5	-80	20	10
22	2	0,7	60	-30	12
23	3	0,6	20	40	-14
24	4	0,3	-50	25	10
25	5	0,2	60	-32	-18
26	6	0,1	-70	26	20
27	7	0,5	80	-48	30
28	8	0,6	50	19	-24
29	9	0,3	-60	26	32
30	10	0,4	70	-35	15
31	11	0,5	-80	20	10
32	12	0,7	60	-30	12
33	13	0,6	20	40	-14
34	14	0,3	-50	25	10
35	15	0,2	60	-32	-18
36	16	0,1	-70	26	20
	а	в	в	а	б

Схема «а» Схема «б»

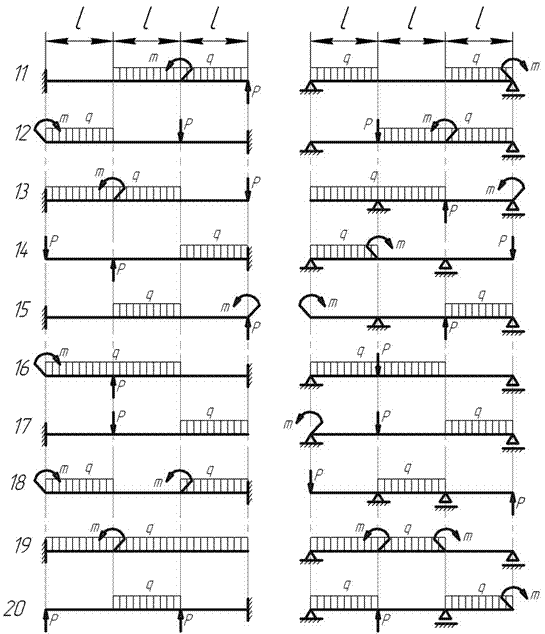
Рис.9

Задача 10. Подбор сечения стальной балки при плоском изгибе из условия прочности

Для стальной балки (рис.10) требуется:

1) подобрать из расчета на прочность по наибольшим напряжениям размеры сечений трех типов (см. рис. 10):

– двутавровое поперечное сечение;

– прямоугольное сечение высотой h=2b;

– круглое поперечное сечение диаметром d;

2) для каждого типа сечения балки вычислить наибольшие касательные напряжения в поперечном сечении;

3) вычертить найденные сечения в одном масштабе на миллиметровой бумаге формата А4, показать размеры сечений, изобразить распределение нормальных и касательных напряжений;

4) найти соотношение весов соответствующих балок G_{двутавра}:G_{прямоугольника}:G_круга, приняв вес двутавровой балки за единицу G_{двутавра}= 1.

Принять: длину l=0,7 м, остальные исходные данные взять из табл. 10 и рис.10.

Таблица 10

Номер cтроки	Схема по рис.10	l1/l	q, кН/м	k	[n]	Материал
01	I	1,0	50	0,75	1,75	Сталь 5 (σТ=280 мПа)
02	II	2,0	80	0,75	2,00	Сталь 3 (σТ=230 мПа)
03	I	3,0	40	0,25	1,50	Сталь 5 (σТ=280 мПа)
04	II	4,0	50	0,75	1,75	Сталь 20 (σТ=220 мПа)
05	I	1,0	80	0,25	2,00	Сталь 40 (σТ=320 мПа)
06	II	2,0	40	0,75	1,50	Сталь 45 (σТ=320 мПа)
07	I	3,0	50	0,75	1,75	Сталь 4 (σТ=240 мПа)
08	II	4,0	80	0,25	2,00	Сталь 3 (σТ=230 мПа)
09	I	2,0	50	0,75	1,50	Сталь 40 (σТ=320 мПа)
10	II	4,0	40	0,25	2,50	Сталь 3 (σТ=230 мПа)
11	I	1,0	50	0,75	1,75	Сталь 5 (σТ=280 мПа)
12	II	2,0	80	0,75	2,00	Сталь 3 (σТ=230 мПа)
13	I	3,0	40	0,25	1,50	Сталь 5 (σТ=280 мПа)
14	II	4,0	50	0,75	1,75	Сталь 20 (σТ=220 мПа)
15	I	1,0	80	0,25	2,00	Сталь 40 (σТ=320 мПа)
16	II	2,0	40	0,75	1,50	Сталь 45 (σТ=320 мПа)
17	I	3,0	50	0,75	1,75	Сталь 4 (σТ=240 мПа)
18	II	4,0	80	0,25	2,00	Сталь 3 (σТ=230 мПа)
19	I	2,0	50	0,75	1,50	Сталь 40 (σТ=320 мПа)
20	II	4,0	40	0,25	2,50	Сталь 3 (σТ=230 мПа)
21	I	1,0	50	0,75	1,75	Сталь 5 (σТ=280 мПа)
22	II	2,0	80	0,75	2,00	Сталь 3 (σТ=230 мПа)
23	I	3,0	40	0,25	1,50	Сталь 5 (σТ=280 мПа)
24	II	4,0	50	0,75	1,75	Сталь 20 (σТ=220 мПа)
25	I	1,0	80	0,25	2,00	Сталь 40 (σТ=320 мПа)
26	II	2,0	40	0,75	1,50	Сталь 45 (σТ=320 мПа)
27	I	3,0	50	0,75	1,75	Сталь 4 (σТ=240 мПа)
28	II	4,0	80	0,25	2,00	Сталь 3 (σТ=230 мПа)
29	I	2,0	50	0,75	1,50	Сталь 40 (σТ=320 мПа)
30	II	4,0	40	0,25	2,50	Сталь 3 (σТ=230 мПа)
31	I	1,0	50	0,75	1,75	Сталь 5 (σТ=280 мПа)
32	II	2,0	80	0,75	2,00	Сталь 3 (σТ=230 мПа)
33	I	3,0	40	0,25	1,50	Сталь 5 (σТ=280 мПа)
34	II	4,0	50	0,75	1,75	Сталь 20 (σТ=220 мПа)
35	I	1,0	80	0,25	2,00	Сталь 40 (σТ=320 мПа)
36	II	2,0	40	0,75	1,50	Сталь 45 (σТ=320 мПа)
	б	а	в	а	г	в

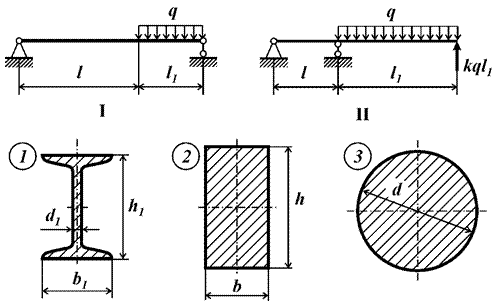
Рис.10

Задача 11. Подбор сечения стальной балки при плоском изгибе из условия прочности

Для стальной балки (рис. 11) требуется:

1) подобрать из расчета на прочность по наибольшим напряжениям размеры сечений трех типов (см. рис. 11):

– тип 1: сечение, составленное из швеллеров или двутавров;

– тип 2: прямоугольное сечение с отношением высоты к ширине h₂/b₂ равным отношению h/b для сечения 1 типа

– тип 3: круглое поперечное сечение;

2) для каждого типа сечения балки вычислить наибольшие касательные напряжения в поперечном сечении;

3) вычертить найденные сечения в одном масштабе на миллиметровой бумаге формата А4, показать размеры сечений, изобразить распределение нормальных и касательных напряжений;

4) найти соотношение весов соответствующих балок G_{двутавра}:G_{прямоугольника}:G_круга, приняв вес двутавровой балки за единицу G_{двутавра}= 1.

Принять: длину l = 0,5 м, остальные исходные данные взять из табл. 11 и рис. 11.

Таблица 11

Номер cтроки	Схема по рис.11	Вариант сечения по рис.11	l1/l	l2/l	q, кН/м	F1/ql	F2/ql	[n]	Материал
01	а)	I	1,0	1,0	50	3,0	1,0	1,75	Сталь 5 (σТ=280 мПа)
02	б)	II	1,5	2,0	100	2,5	1,5	2,00	Сталь 3 (σТ=230 мПа)
03	а)	III	2,0	2,5	80	2,0	–1,5	1,50	Сталь 5 (σТ=280 мПа)
04	б)	I	1,5	1,5	70	1,5	1,5	1,75	Сталь 20 (σТ=220 мПа)
05	а)	II	2,0	1,0	60	–2,0	–2,0	2,00	Сталь 40 (σТ=320 мПа)
06	а)	III	2,5	2,5	90	–2,5	2,5	1,50	Сталь 45 (σТ=320 мПа)
07	б)	I	1,5	1,5	80	–2,0	–2,5	1,75	Сталь 4 (σТ=240 мПа)
08	б)	II	2,0	2,0	60	–1,5	1,5	2,00	Сталь 3 (σТ=230 мПа)
09	а)	III	2,0	1,0	80	–3,0	2,0	1,50	Сталь 40 (σТ=320 мПа)
10	б)	I	1,0	1,5	70	2,0	–1,0	2,50	Сталь 3 (σТ=230 мПа)
11	а)	II	1,0	1,0	50	3,0	1,0	1,75	Сталь 5 (σТ=280 мПа)
12	б)	III	1,5	2,0	100	2,5	1,5	2,00	Сталь 3 (σТ=230 мПа)
13	а)	I	2,0	2,5	80	2,0	–1,5	1,50	Сталь 5 (σТ=280 мПа)
14	б)	II	1,5	1,5	70	1,5	1,5	1,75	Сталь 20 (σТ=220 мПа)
15	а)	III	2,0	1,0	60	–2,0	–2,0	2,00	Сталь 40 (σТ=320 мПа)
16	а)	I	2,5	2,5	90	–2,5	2,5	1,50	Сталь 45 (σТ=320 мПа)
17	б)	II	1,5	1,5	80	–2,0	–2,5	1,75	Сталь 4 (σТ=240 мПа)
18	б)	III	2,0	2,0	60	–1,5	1,5	2,00	Сталь 3 (σТ=230 мПа)
19	а)	I	2,0	1,0	80	–3,0	2,0	1,50	Сталь 40 (σТ=320 мПа)
20	б)	II	1,0	1,5	70	2,0	–1,0	2,50	Сталь 3 (σТ=230 мПа)
21	а)	III	1,0	1,0	50	3,0	1,0	1,75	Сталь 5 (σТ=280 мПа)
22	б)	I	1,5	2,0	100	2,5	1,5	2,00	Сталь 3 (σТ=230 мПа)
23	а)	II	2,0	2,5	80	2,0	–1,5	1,50	Сталь 5 (σТ=280 мПа)
24	б)	III	1,5	1,5	70	1,5	1,5	1,75	Сталь 20 (σТ=220 мПа)
25	а)	I	2,0	1,0	60	–2,0	–2,0	2,00	Сталь 40 (σТ=320 мПа)
26	а)	II	2,5	2,5	90	–2,5	2,5	1,50	Сталь 45 (σТ=320 мПа)
27	б)	III	1,5	1,5	80	–2,0	–2,5	1,75	Сталь 4 (σТ=240 мПа)
28	б)	I	2,0	2,0	60	–1,5	1,5	2,00	Сталь 3 (σТ=230 мПа)
29	а)	II	2,0	1,0	80	–3,0	2,0	1,50	Сталь 40 (σТ=320 мПа)
30	б)	III	1,0	1,5	70	2,0	–1,0	2,50	Сталь 3 (σТ=230 мПа)
31	а)	I	1,0	1,0	50	3,0	1,0	1,75	Сталь 5 (σТ=280 мПа)
32	б)	II	1,5	2,0	100	2,5	1,5	2,00	Сталь 3 (σТ=230 мПа)
33	а)	III	2,0	2,5	80	2,0	–1,5	1,50	Сталь 5 (σТ=280 мПа)
34	б)	I	1,5	1,5	70	1,5	1,5	1,75	Сталь 20 (σТ=220 мПа)
35	а)	II	2,0	1,0	60	–2,0	–2,0	2,00	Сталь 40 (σТ=320 мПа)
36	а)	III	2,5	2,5	90	–2,5	2,5	1,50	Сталь 45 (σТ=320 мПа)
	б	в	а	г	в	а	б	г	в

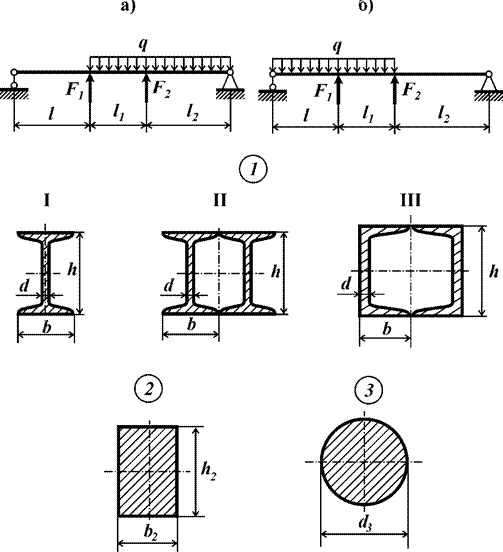
Рис.11

Задача 12. Подбор сечения деревянной (стальной) балки, работающей в условиях плоского поперечного изгиба

Исходные данные к задаче выбираются по табл. 12.1 (12.2) и схемам на рис.12.

1. Нарисуйте схему балки в масштабе. Отрицательные нагрузки направьте в сторону, противоположную показанной на рисунке. На рисунке поставьте размеры балки и значения нагрузки в численном виде.

2. Найдите опорные реакции.

3. Постройте в масштабе эпюры распределения внутренних усилий Q и M по длине стержня.

4. Нарисуйте фасад балки и эпюры распределения нормальных и касательных напряжений по высоте сечения. На фасаде покажите опасные точки.

5. Из условия прочности опасной точки, в которой действуют максимальные нормальные напряжения, найдите размеры поперечного сечения балки. (Для деревянных балок круглого поперечного сечения диаметр бревен не должен превышать ходового размера d ≤ 26 см. Если это условие не выполняется, подберите сечение из нескольких бревен.)

6. Убедитесь в том, что найденный размер поперечного сечения обеспечивает выполнение условия прочности в точке, где действуют максимальные касательные напряжения.

7*. Для сечений из 2-3 бревен сравните расход материала для различных вариантов расположения бревен в поперечном сечении: горизонтальном, вертикальном и других.

Таблица 12.1

Номер строки	Схема по рис.12	F0, кН	F1, кН	F2, кН	l1, м	M0, кНм	M1, кНм	M2, кНм	Сечение	h/b	l2, м	Интенсивность распределенной нагрузки, кН/м
												Вариант 1		Вариант 2
												q01=q11=q1	q02=q12=q2	q01	q11	q02	q12
1	3	5	0	0	0,4	0	0	20	Круг	-	2,0	20	20	20	20	0	-20
2	1	0	-5	0	1,0	0	-20	0	Квадрат	2,0	1,0	-10	-10	0	-10	20	20
3	2	0	0	10	3,0	20	0	0	Круг	-	2,0	20	-20	10	10	-20	0
4	2	0	0	-10	4,0	0	10	0	Квадрат	2,5	1,0	-10	10	-10	-10	0	20
5	3	-10	0	0	0,5	0	0	-10	Круг	-	2,0	5	-5	-10	0	-10	-10
6	1	0	10	0	2,0	-10	0	0	Квадрат	1,5	1,0	5	5	5	5	10	0
7	3	20	0	0	0,6	0	-10	0	Круг	-	2,0	-20	10	0	-20	10	10
8	1	0	-20	0	3,0	0	0	30	Квадрат	3,0	1,0	10	-20	10	10	0	-20
9	2	0	0	30	2,0	0	30	0	Круг	-	2,0	-20	10	20	0	-10	-10
0	3	-30	0	0	0,8	-20	0	0	Квадрат	2,0	1,0	-5	20	-5	-5	20	0
	а	в	а	г	б	в	а	г	б	в	а	г	б	в	а	г	б

Таблица 12.2

Номер строки	Схема по рис.12	F0, кН	F1, кН	F2, кН	l1, м	M0, кНм	M1, кНм	M2, кНм	Сечение	h/b	l2, м	Интенсивность распределенной нагрузки, кН/м
												q01	q11	q02	q12
01	1	0	5	0	0,5	0	0,5	0	Квадрат	1,5	1,0	2	2	0	-5
02	2	0	0	-5	0,8	0	0	-0,5	Круг	-	0,5	4	0	3	3
03	3	2	0	0	0,3	-0,4	0	0	Квадрат	2,0	1,0	0	5	1	1
04	3	-2	0	0	0,4	0	0	0,4	Круг	-	0,5	-2	-2	5	0
05	1	0	-2	0	1,0	0	0,8	0	Квадрат	2,5	1,0	5	0	-1	-1
06	2	0	0	3	0,9	-0,8	0	0	Круг	-	0,5	4	4	2	0
07	1	0	3	0	0,6	0	-1,0	0	Квадрат	3,0	1,0	0	-8	2	2
08	3	1	0	0	0,2	0	0	1,0	Круг	-	0,5	-3	-3	0	8
09	1	0	4	0	0,7	2,0	0	0	Квадрат	2,0	1,0	2	2	0	-10
10	2	0	0	-4	0,8	0	0	-2,0	Круг		0,5	10	0	-4	-4
	а	б	в	г	а	б	в	г	а	б	в	г	г	а	б

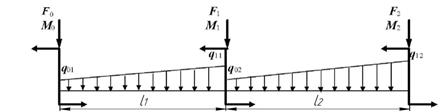
1 схема

2 схема

3 схема

Рис. 12

Задача 13. Подбор сечения стальной двутавровой балки, работающей в условиях плоского поперечного изгиба

Исходные данные к задаче выбираются по табл. 13 и схемам на рис. 13.

1. Нарисуйте схему балки в масштабе. Отрицательные нагрузки направьте в сторону, противоположную показанной на рисунке. На рисунке поставьте размеры балки и значения нагрузки в численном виде.

2. Найдите опорные реакции.

3. Постройте в масштабе эпюры распределения внутренних усилий Q и M по длине стержня.

4. Нарисуйте фасад балки и эпюры распределения нормальных и касательных напряжений по высоте двутавра. На фасаде покажите опасные точки.

5. Из условия прочности опасной точки, в которой действуют максимальные нормальные напряжения, найдите номер двутавра.

6. Проверьте прочность в остальных опасных точках. Если условие прочности в какой-нибудь точке не будет выполняться, подберите новый номер двутавра.

7*. Найдите напряженное состояние произвольной точки двутавра, находящейся в сечении, где Q и M не равны нулю. Покажите напряженное состояние этой точки на рисунке. Определите главные напряжения графическим способом и покажите на рисунке, на каких площадках они действуют.

8*. Исследуйте напряженное состояние в семи точках по высоте двутавра (крайние точки, точка на нейтральной оси, точки на сопряжении полок со стенкой и точки, расположенные на расстоянии, равном четверти высоты двутавра, от нейтральной оси). Для этого:

- вычислите нормальные и касательные напряжения и постройте эпюры распределения этих напряжений по высоте двутавра;

- определите главные и максимальные касательные напряжения и постройте эпюры их изменения по высоте балки (все эпюры напряжений рекомендуется строить в одном масштабе).

Подсчеты удобно производить в табличной форме.

№ точки	z, см	b, см	S^оy, см^3	σ, МПа	τ, МПа	Главные напряжения, МПа		τmax, МПа
						σ1	σ3

9*. Подберите сечение двутавра расчетом по предельному пластическому состоянию.

Таблица 13

Интенсивность распределенной нагрузки, кН/м						Схема по рис.13	l1, м	l3, м	F0, кН	F1, кН	F2, кН	F3, кН	l2, м	q3, кН/м	M1 кНм	M2 кНм
Вариант 1		Вариант 2
q01=q11 =q1	q02=q12=q2	q01	q11	q02	q12
20	0	20	0	0	0	4	2	1	20	0	0	0	3	20	0	30
0	10	0	0	0	10	3	1	4	40	0	0	0	4	30	40	0
-30	0	-30	0	0	0	2	5	1	0	30	0	0	5	-30	50	0
40	0	0	40	0	0	1	2	2	0	0	30	0	6	-20	0	40
0	-20	0	0	-20	0	4	1	2	-40	0	0	0	7	5	-60	0
0	20	0	0	0	20	3	1	3	-50	0	0	0	8	-5	-30	0
-10	0	0	-10	0	0	2	3	2	0	0	0	-30	6	10	0	50
10	0	10	0	0	0	1	3	2	0	-20	0	0	5	-10	0	-50
0	-30	0	0	30	0	3	2	3	30	0	0	0	4	40	20	0
0	30	0	0	0	-30	4	1	1	-30	0	0	0	3	-40	-20	0
а	г	в	б	а	г	в	б	а	г	б	в	а	г	б	в	а

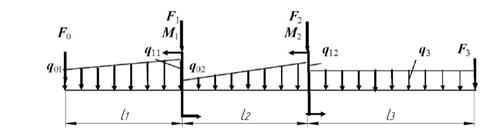
1 схема

2 схема

3 схема

4 схема

Рис. 13

Задача 14. Подбор сечения и определение перемещений двутавровой балки при плоском изгибе

Исходные данные к задаче принимаются по табл. 14 и схемам на рис. 14.

1. Нарисуйте схему балки в масштабе. Отрицательные нагрузки направьте в сторону, противоположную показанной на рис. 14. На рисунке поставьте размеры балки и значения нагрузки в численном виде.

2. Постройте эпюры Q и M. Из условия прочности подберите номер двутавра. Убедитесь в том, что условия прочности выполняются во всех опасных точках.

3. Определите прогиб и угол поворота в сечениях, заданных в табл. 14, аналитическим способом. Для этого:

- составьте приближенное дифференциальное уравнение изогнутой оси балки и проинтегрируйте его, получив выражения для угла поворота и прогиба балки в произвольном сечении;

- найдите из граничных условий постоянные интегрирования;

- определите прогиб и угол поворота в требуемых сечениях.

4. Определите прогиб и угол поворота в сечениях, заданных в табл. 14, методом Максвелла - Мора. Для этого:

- приложите единичные обобщенные силы, соответствующие искомым перемещениям, и постройте эпюры изгибающих моментов от действия этих единичных сил;

- проинтегрируйте приближенную формулу Максвелла - Мора либо аналитически, либо по правилу Верещагина (по формуле Симпсона).

5. Покажите на рисунке изогнутую ось балки и отметьте на ней найденные перемещения.

6. Проверьте жесткость балки. Если условие жесткости не выполняется, измените номер двутавра так, чтобы оно выполнялось.

7*.Оцените влияние поперечной силы на прогиб.

Таблица 14

Номер строки	q1, кН/м	q2, кН/м	l2, м	M1, кНм	M2, кНм	l1, м	l3, м	Угол поворота в сечении	Схема по рис. 14	Прогиб в сечении	q3, кН/м	F0, кН	F1, кН	F2, кН	F3, кН
01	10	0	6	20	0	1	1	1	3	2	0	0	20	-30	0
02	0	10	2	0	20	1	2	2	1	0	0	40	0	-20	0
03	-20	0	4	-30	0	2	1	1	4	2	0	50	0	-10	0
04	0	-20	4	0	-30	1	2	2	5	1	0	0	-40	0	60
05	30	0	2	40	0	2	2	1	2	3	0	0	0	30	-40
06	0	30	6	0	40	2	2	2	6	3	10	-60	0	0	0
07	5	0	4	-50	0	1	1	1	3	1	0	0	-10	30	0
08	0	5	4	0	-50	1	2	2	1	1	0	-40	0	10	0
09	20	0	6	60	0	1	1	1	4	0	0	-50	0	20	0
10	0	20	2	0	60	2	1	2	5	3	-10	0	-60	0	0
	а	в	г	б	а	в	г	б	а	в	г	б	а	в	г

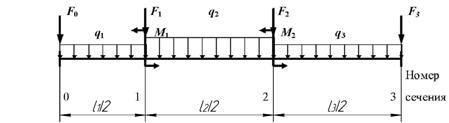
1 схема

2 схема

3 схема

4 схема

5 схема

6 схема

Рис. 14

Примеры выполнения задач

Пример 1

Для заданной балки при указанных на схеме нагрузках и размерах балки, форме поперечного сечения требуется:

1. разбить балку на участки, обозначив длину каждого из них;

2. определить реакции опор;

3. записать аналитические выражения для внутренних усилий на каждом участке;

4. построить эпюры внутренних усилий в выбранном масштабе;

5. по эпюре определить максимальный по модулю изгибающий момент и назначить размеры поперечного сечения, используя условие прочности по нормальным напряжениям;

6. записать уравнения метода начальных параметров для моментов, углов поворота сечений и прогибов;

7. построить эпюры углов поворота и прогибов;

8. проверить правильность построения эпюр по дифференциальным зависимостям между моментами, углами поворота и прогибами;

9. найти максимальный по модулю прогиб и назначить размеры поперечного сечения по условию жесткости;

10. назначить окончательные размеры поперечного сечения по условиям прочности и жесткости.

Дополнительно для всех вариантов принять: форму поперечного сечения балки – стандартный двутавровый профиль; расчетное сопротивление стали R = 200 МПа; нормативный прогиб [v] = a/300; модуль упругости стали E = 2∙10⁵ МПа.

Примечание: Данные для решения задачи взять в табл. 15, на рис. 15.

Таблица 15

a, м	q, кН/м	F, кН	M, кНм
1,5	15	20	25

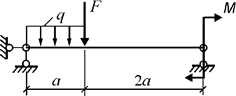
Рис. 15. Схема балки

Решение.

Определение реакций опор

Из уравнений статики всей балки (рис.16) определяются реакции R_A и R_B.

ΣM_B = 0. R_A∙3a - q∙a(0,5a +2a) - F∙2a + M = 0.

ΣF_y = 0. R_A - q∙a - F + R_B = 0.

Отсюда

R_A = (q∙2,5a² + F∙2a - M) = (15∙2,5∙1,5² + 20∙2∙1,5 - 25) = 26,53 кН,

R_B = - R_A + q∙a + F = - 26,53 + 15∙1,5 + 20 = 15,97 кН.

Рис. 16. Расчетная схема балки

Построение эпюр внутренних усилий

Участок 1: 0 ≤ z₁ ≤ a.

Выражения для Q(z₁) и М(z₁), полученные из уравнений равновесия левой оставляемой для рассмотрения части балки (см. рис. 16):

Q(z₁) = - { R_A - q∙z₁};

М(z₁) = - { R_A∙z₁ - q∙z₁∙}.

Для построения эпюр вычисляются значения Q и М в характерных точках участка 1.

Q(0) = - R_A = - 26,53 кН.

Q(a) = - R_A + q∙a = - 26,53 + 15∙1,5 = - 4,03 кН.

М(0) = 0.

М(0,5a) = - R_A∙0,5a + 0,5q(0,5a)² = - 26,53∙0,5∙1,5 + 0,5∙15(0,5∙1,5)² = - 15,68 кНм.

М(a) = - R_A∙a + q∙a² = - 26,53∙1,5 + 15∙1,5² = - 22,92 кНм.

Участок 2: 0 ≤ z₂ ≤ 2a.

Выражения для Q(z₂) и М(z₂), полученные из уравнений равновесия левой оставляемой для рассмотрения части балки (см. рис. 16):

Q(z₂) = - { R_A - q∙a - F};

М(z₂) = - { R_A(a + z₂) - q∙a(0,5a + z₂) - F∙z₂}.

Для построения эпюр вычисляются значения Q и М в характерных точках участка 2.

Q = const = - R_A + q∙a + F = - 26,53 + 15×1,5 + 20 = 15,97 кН.

М(0) = - R_A∙a + 0,5q∙a² = - 26,53∙1,5 + 0,5∙15∙1,5² = - 22,92 кНм.

М(2a) = - R_A∙3a + q∙a(0,5a + 2a) + F∙2a = - 26,53∙3∙1,5 + 15∙1,5∙2,5∙1,5 + 20∙2∙1,5 = 25,0 кНм.

Эпюры Q и М, построенные по вычисленным значениям внутренних усилий в выбранных точках участков, изображены на рис.17.

Рис. 17. Эпюры Q и M

Определение размеров сечения по условию прочности

По эпюре изгибающих моментов (рис. 17) находится наибольший по модулю (расчетный) момент M_max = 25,0 кНм.

Определяется необходимый момент сопротивления сечения при изгибе

W_и ≥ = 1,25∙10^-4 м³ = 125 см³.

По таблице стандартных прокатных профилей (см. раздел «Справочные данные») выбирается и назначается двутавровый профиль № 18, у которого W_и = 143 см³.

Составление уравнений метода начальных параметров для изгибающих моментов, углов поворота сечений и прогибов

В соответствии с правилами составления универсальных уравнений распределенная нагрузка q, действующая только на участке 1, продлевается до конца балки, т.е. до конца участка 2, а на участке 2 прикладывается нагрузка q противоположного направления (рис. 18).

Рис. 18. Схема для составления универсальных уравнений

Таким образом, на участке 2, свободном от нагрузки q, продленная и вновь приложенная нагрузки уравновешены и обе заканчиваются в конце балки. Координаты сечений z на участках 1 и 2 отсчитываются от начала балки. По схеме, изображенной на рис. 16, составляется аналитическое выражение для изгибающих моментов на участках 1 и 2 в форме одного универсального уравнения

M(z) = - R_A∙z + q∙ + F(z - a) - q∙. (1)

Интегрированием дифференциального соотношения

с учетом формулы (1) находится выражение для определения углов поворота сечений:

(2)

где EJ𝜑₀ - постоянная интегрирования, пропорциональная углу поворота φ₀ = φ (0).

Интегрированием дифференциального уравнения

с учетом равенства (2) получается выражение для определения прогибов:

(3)

где EJv₀ - постоянная интегрирования, пропорциональная прогибу в начале координат, т.е. прогибу v₀ = v(0).

Определение постоянных EJ𝛗₀ и EJv₀

Из анализа закрепления оси балки (рис. 16) составляются условия в точках закрепления:

EJv(0) = 0;

EJv(3a) = 0. (4)

Используя условия (4) и равенство (3), записываются два уравнения, содержащих две искомые константы:

EJv₀ = 0,

Решением этой системы уравнений определяются значения постоянных:

EJv₀ = 0;

EJ𝜑₀ = 23,836 кНм².

Построение эпюр EJ𝝋 (z) и EJv(z)

Для построения эпюры EJ𝜑 (z) вычисляются значения этой функции в характерных точках участков 1 и 2 по выражению (2).

EJ𝜑 (0) = EJ𝜑₀ = 23,836 кНм².

EJ𝜑 (0,5a) = 23,836 - 26,53∙ + 15∙ = 17,429 кНм².

EJ𝜑 (a) = 23,836 - 26,53∙ + 15∙ = 2,427 кНм².

EJ𝜑 (1,5a) = 23,836 - 26,53∙ + 15∙ + 20∙ - 15∙ = - 10,271 кНм².

EJ𝜑 (2a) = 23,836 - 26,53∙ + 15∙ + 20∙ - 15∙ = - 13,987 кНм².

EJ𝜑 (2,5a) = 23,836 - 26,53∙ + 15∙ + 20∙ - 15∙ = - 8,719 кНм².

EJ𝜑 (3a) = 23,836 - 26,53∙ + 15∙ + 20∙ - 15∙ = 5,532 кНм².

Для построения эпюры EJv(z) вычисляются значения этой функции в характерных точках участков 1 и 2 по выражению (3).

EJv(0) = EJv₀ = 0.

EJv(0,5a) = - 23,836∙0,5∙1,5 + 26,53∙ - 15∙ = - 16,209 кНм³.

EJv(a) = - 23,836∙1,5 + 26,53∙ - 15∙ = - 16,209 кНм³.

EJv(1,5a) = - 23,836∙1,5∙1,5 + 26,53∙ - 15∙ - 20∙ + 15∙ = - 23,995 кНм³.

EJv(2a) = - 23,836∙2∙1,5 + 26,53∙ - 15∙ - 20∙ + 15∙ = - 10,834 кНм³.

EJv(2,5a) = - 23,836∙2,5∙1,5 + 26,53∙ - 15∙ - 20∙ + 15∙ = - 1,758 кНм³.

EJv(3a) = - 23,836∙3∙1,5 + 26,53∙ - 15∙ - 20∙ + 15∙ = 0.

Дополнительно вычисляются значения EJv(z) в точках, близких к точке смены знака функции EJφ(z).

EJv(1,05a) = - 23,836∙1,05∙1,5 + 26,53∙ - 15∙ - 20∙ + 15∙ = - 24,114 кНм³.

EJv(1,1a) = - 23,836∙1,1∙1,5 + 26,53∙ - 15∙ - 20∙ + 15∙ = - 24,110 кНм³.

Эпюры EJ𝜑 (z) и EJv(z), построенные по вычисленным значениям этих функций в выбранных точках участков, изображены на рис. 19.

Рис. 19. Эпюры изгибающих моментов,

относительных углов поворота сечений и прогибов

Определение размеров сечения по условию жесткости

По эпюре относительных прогибов определяется расчетная величина (EJv)_max (см. рис. 19).

(EJv)_max = 24,115 кНм³.

Находится требуемый момент инерции сечения

По таблице стандартных прокатных профилей (см., раздел «Справочные данные») выбирается и назначается двутавровый профиль № 22, у которого J = 2550 см⁴.

Установление размеров сечения балки по условиям прочности и жесткости

Из расчетов размеров сечения по условиям прочности и жесткости окончательно устанавливается двутавровый профиль № 22, обеспечивающий и прочность, и жесткость балки.

Пример 2

Требуется построить эпюры поперечных сил и изгибающих моментов и подобрать размеры поперечного сечения стальной балки (рис. 20) для различных форм сечения: двутавровой балки, балки прямоугольного сечения со сторонами h и b при h/b = 2 и круглого поперечного сечения. Балка выполнена из стали с допускаемым напряжением [σ] =190 МПа; а =1 м; q=10 кН/м.

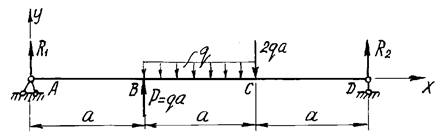
Рис. 20. Расчетная схема балки

1. Определение опорных реакций.

На схеме показываем опорные реакции R₁, H, R₂ . Вертикальные реакции направляем вверх и записываем уравнения равновесия:

ΣX=0; H=0;

ΣM_D=0; R₁3a+qa∙2a-qa∙1,5a-2qa∙a=0.

Отсюда R₁=0,5qa.

ΣM_A=0; R₂3a-2qa∙2a-qa∙1,5a+qa∙a=0.

Отсюда R₂=1,5qa.

Проверим правильность вычислений, составив еще одно уравнение равновесия:

ΣY=0; 0,5qa+qa-qa-2qa+1,5qa=0.

Условие равновесия удовлетворяется, реакции определены правильно.

2.Построение эпюры Q.

Мысленно разбиваем балку на участки. Границами участков являются сечения, в которых к балке приложены сосредоточенные силы или пары сил, начинаются или заканчиваются распределенные нагрузки, имеются промежуточные шарниры. В рассматриваемой балке граничными сечениями будут сечения A, B, C и D. Для каждого из трех участков запишем аналитическое выражение Q(x).

Участок AB, 0<x<a. Рассмотрим произвольно выбранное сечение с абсциссой x. Рассекая балку в этом сечении на две части и отбросив правую часть, вычисляем алгебраическую сумму проекций на ось y всех сил, действующих на оставшуюся часть:

Q(x)=R₁=0,5qa.

Поперечная сила не зависит от переменной x на протяжении всего участка, следовательно, эпюра Q ограничена прямой, параллельной оси абсцисс. Отложив от оси эпюры вверх в выбранном масштабе 0,5qa (рис.21), строим эпюру на этом участке.

Участок BC, a<x<2a. Алгебраическая сумма проекций всех сил на ось y слева от сечения с абсциссой x

Q(x)=0,5qa+qa-q(x-a)=1,5qa-q(x-a).

Полученное выражение является уравнением наклонной прямой, которая может быть построена по двум лежащим на ней точкам. Для ее построения найдем значения поперечной силы на границах участков балки

x=a, Q(a)=1,5qa,

x=2a, Q(2a)=0,5qa.

Участок CD, 2a<x<3a. Поперечная сила на расстоянии x от начала координат

Q(x)=0,5qa+qa-qa-2qa=-1,5qa.

Так как поперечная сила не зависит от переменной x, на последнем участке эпюра Q ограничена прямой, параллельной оси балки (см. рис. 21).

3. Построение эпюры M_z.

Аналитическое выражение для вычисления изгибающего момента в сечении x необходимо записать для каждого участка балки.

Участок AB:

M_z(x)=0,5qa∙x.

На этом участке балки изгибающий момент возрастает по линейному закону и эпюра M_z ограничена наклонной прямой. Вычисляя его значения в сечениях на границах участка, строим в масштабе (рис. 21) эпюру M_z на сжатом волокне

x=0, M_z(0)=0;

x=a, M_z(a)=0,5qa².

Участок BC:

Полученное уравнение является уравнением квадратной параболы и, поскольку поперечная сила Q на участке BC не изменяет знак, экстремума на эпюре M_z не будет.

Определим изгибающий момент на границах участка:

x=a, M_z(a)=0,5qa²;

x=2a, M_z(2a)=0,5qa∙2a+qa(2a-a)-

Отложив вверх от оси балки найденные значения, проводим квадратную параболу выпуклостью вверх (навстречу вектору усилия равномерно распределенной нагрузки).

Участок CD:

M_z(x)=0,5qa∙x+qa(x-a)-qa(x-1,5a)-2qa(x-2a).

В пределах последнего участка балки (2a<x<3a) изгибающий момент линейно зависит от абсциссы x, и эпюра ограничена прямой линией.

При x=2a, M_z(2a)=1,5qa², при x=3a, M_z(3a)=0.

Эпюры Q и M_z показаны на рис. 21.

z

Рис. 21. Расчетная схема балки. Эпюры поперечных сил и изгибающих моментов

По эпюре M_z находим опасное сечение балки - сечение, в котором изгибающий момент максимален по абсолютной величине. Для заданной балки изгибающий момент в опасном сечении = M_z(2a)=1,5qa² или после подстановки числовых значений =1,5∙10∙1²= 15 кНм.

Из условия прочности определим требуемый момент сопротивления сечения

Номер двутавра находим по расчетному значению момента сопротивления W_z, используя таблицы сортамента прокатной стали.

Внимание! В таблицах сортамента прокатной стали (см. «справочные данные») оси z соответствует ось x , это означает, что W_z=W_x.

Наиболее близок к требуемому момент сопротивления двутавра №14, равный W_x= 81,7 см³. Выбрав это сечение, определяем нормальные напряжения в поперечном сечении балки:

Подбираем прямоугольное сечение, момент сопротивления которого определяется с учетом того, что h=2b:

Отсюда

Круглое поперечное сечение имеет момент сопротивления

Диаметр круга

Рассмотрим второй метод построения эпюр внутренних усилий, действующих в сечениях балки. Он состоит в том, что поперечные силы и изгибающие моменты вычисляются на границах участков без записи уравнений Q(z), M(z), а соответствующие эпюры строятся на основании дифференциальных зависимостей между Q, M, q:

Зависимости (1) позволяют установить следующие характерные особенности эпюр поперечных сил и изгибающих моментов:

На участках, где нет распределенной нагрузки, эпюра Q ограничена прямыми, параллельными оси балки, а эпюра M - наклонными прямыми.

На участках, где приложена равномерно распределенная нагрузка интенсивностью q, эпюра Q ограничена наклонными прямыми, а эпюра M - квадратными параболами, выпуклость которых направлена навстречу вектору равномерно распределенной нагрузки.

На участках, где Q >0, изгибающий момент возрастает; если Q<0 - изгибающий момент убывает.

В сечениях, где к балке приложены сосредоточенные силы, на эпюре Q будут скачки на величину приложенных сил, а на эпюре M - переломы, острие которых направлено против действия этих сил.

В сечениях, где к балке приложены пары сил (сосредоточенные моменты), на эпюре M будут скачки на величину этих моментов.

Если на участке балки имеется равномерно распределенная нагрузка и эпюра Q в пределах участка изменяет знак, то в сечении, где Q = 0, на эпюре M_z будет экстремум.

Примеры использования дифференциальных зависимостей при расчете балок приводятся ниже.

Пример 3

Рассмотрим задачу подбора сечения балки, изготовленной из хрупкого материала. Балка (рис.22) изготавливается из чугуна и имеет сечение, показанное на рис.24.

Требуется определить из расчета на прочность по допускаемым напряжениям размеры поперечного сечения, если материал балки - чугун с допускаемым напряжением на сжатие [σ]_сж=700 МПа и на растяжение [σ]_р=140 МПа; a=1 м; q= 10 кН/м.

Рис. 22. Расчетная схема чугунной балки

Решение.

Для нахождения опасного сечения строим эпюры M и Q. Очевидно, что данная балка имеет три участка:

AB (0≤x≤a), BC (a≤x≤2a), CD (2a≤x≤3a).

Для того чтобы не вычислять опорные реакции, рассмотрим балку, начиная с участка AB. Найдем поперечную силу и изгибающий момент в начале этого участка. Мысленно рассечем балку в сечении A на две части и отбросим правую ее часть. Слева на оставшуюся часть действует только сосредоточенная сила, равная 2qa. Проектируя эту силу на нормаль к оси балки, получаем

Q(0) = 2qa.

Рассекая балку в сечении B и поступая аналогично, находим величину поперечной силы в этом сечении - она равна алгебраической сумме проекций сил, действующих на оставшуюся левую часть балки, на нормаль к ее оси:

Q(a) = 2qa-qa qa,

где 2qa - проекция сосредоточенной силы на нормаль к оси балки; qa - проекция равнодействующей распределенной нагрузки.

Изгибающий момент в начале первого участка M (0) = 0; в конце участка он равен алгебраической сумме моментов относительно точки B от сосредоточенной силы 2qa и распределенной нагрузки:

M_z(a)=2qa∙a-qa∙0,5a=1,5qa².

Строим эпюры Q и M_z для первого участка балки.

Выбрав масштаб, откладываем вверх от оси эпюр (Q и M_z положительны!) найденные значения поперечных сил и изгибающих моментов. На эпюре Q соединяем прямой линией точки с координатами (0, 2qa) и (a, qa), а на эпюре M_z проводим квадратную параболу выпуклостью вверх через точки (0, 0) и (a, 1,5qa²).

Поступая аналогично, вычисляем поперечные силы и изгибающие моменты в начале и конце участков BC и CD.

Участок BC: a≤x≤2a;

Q(a) qa, Q(2a)qa;

M(a)1,5qa², M(2a) 2,5qa².

Отложив вверх вычисленные значения Q и M, строим эпюры внутренних усилий на втором участке балки. Как следует из дифференциальных зависимостей, эти эпюры ограничены прямыми линиями.

Участок CD: 2a≤x≤3a;

Q(2a)qa, Q(3a)qa;

M(2a) =4,5qa², M(3a)=5,5qa².

В начале последнего участка к балке приложена пара сил, что вызывает появление скачка на эпюре изгибающих моментов. На участке CD распределенной нагрузки нет, поэтому эпюры Q, M_z ограничены прямыми линиями (рис.23).

Окончательный вид эпюр Q, M_z показан на том же рисунке.

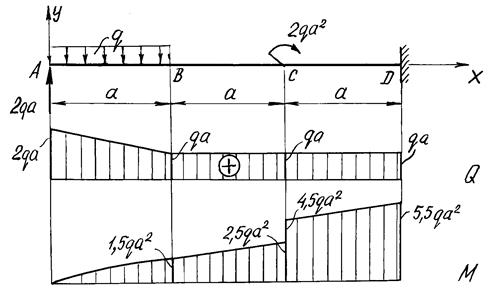
Рис. 23. Расчетная схема балки. Эпюры поперечных сил и изгибающих моментов

Опасное сечение находится в заделке и расчетный изгибающий момент = 5,5qa² =5,5∙10∙1² Нм =55∙10³ Нм = 55 кНм.

Для определения размеров поперечного сечения необходимо найти из условия прочности балки осевой момент сопротивления относительно его нейтральной оси.

Заданное сечение (рис.24) имеет ось симметрии, и для определения положения его центра тяжести достаточно вычислить только одну его координату - ординату у_с.

Разобьем заданную фигуру на две простые части: прямоугольник (1) и полукруг (2). В качестве исходных осей принимаем главные центральные оси прямоугольника y₁, z₁. Тогда ордината центра тяжести всей фигуры определится по формуле

Определив положение центра тяжести, проводим главные центральные оси Y, Z составной фигуры.

Рис. 24. Поперечное сечение чугунной балки

Вычисляем момент инерции заданного сечения относительно главной центральной оси Z:

При расчете на прочность балок, изготовленных из хрупких материалов, для сечений с одной осью симметрии необходимо вычислять два момента сопротивления относительно оси Z:

Из эпюры изгибающих моментов (рис.23), построенной на сжатом волокне, следует, что в опасном сечении верхние волокна балки сжаты, а нижние растянуты. Условие прочности для опасных точек в растянутой зоне сечения имеет вид

Отсюда a = 0,043 м = 4,3 см.

Опасной точкой в сжатой зоне является точка, наиболее удаленная от оси z на расстояние . Условие прочности балки по допускаемым напряжениям на сжатие

Отсюда a = 0,026 м = 2,6 см.

В расчете по нормальным напряжениям из двух найденных значений a принимаем большее (a = 4,3 см), что обеспечивает прочность материала балки как в растянутой, так и в сжатой зонах.

Пример 4.

Рассмотрим пример подбора составного сечения стальной балки.

Для балки (рис.25) подобрать сечение, состоящие из двух стальных швеллеров. Принять а = 1 м; q = 10 кН/м; [σ] =190 МПа.

Рис. 25. Расчетная схема балки

Решение.

Определяем опорные реакции:

ΣM_B=0; R₁2a-qa²-2qa∙a=0; R₁=3qa/2.

ΣM_A=0; R₂2a+2qa∙3a-2qa∙2a+qa²=0. R₂=-3qa/2.

Отметим, что момент распределенной нагрузки относительно опоры B равен нулю, а реакция второй опоры направлена не вверх, как показано на рис.25, а вниз.

Проверка правильности вычисления опорных реакций:

ΣY=0; 3qa/2-2qa-3qa/2+2qa=0.

Реакции определены правильно.

Эпюры Q, M_z строятся аналогично эпюрам предыдущего примера. Вид эпюр показан на рис.26.

Рис. 26. Расчетная схема балки. Эпюры поперечных сил и

изгибающих моментов

По эпюре М_z находим величину изгибающего момента, максимального по модулю

=1,5qa²=1,5∙10∙1²= 15 кНм.

Сечение балки подбираем из условия прочности при изгибе. Требуемый момент сопротивления сечения, состоящего из двух швеллеров

Осевой момент сопротивления одного швеллера будет в два раза меньше – W_z=39,5 см³.

По таблице сортамента прокатной стали находим, что ближайший подходящий момент сопротивления имеет швеллер № 12, для которого W_z=W_x= 50,6 см³. Швеллер № 10 с осевым моментом сопротивления 34,8 см³ принять нельзя, так как в этом случае момент сопротивления сечения, составленного из двух швеллеров, будет равен 69,6 см³<79 см³ и напряжения в балке превысят допускаемые на 13%, что неприемлемо (в расчетах допускается перенапряжение ≤ 5%) .

Рассмотрим пример решения второй части задачи.

Построим эпюры распределения нормальных напряжений по высоте сечения для двух балок - двутавровой стальной и чугунной.

Нормальные напряжения в поперечном сечении балок при изгибе определяются по формуле

По ширине сечения нормальные напряжения распределяются равномерно. Зависимость между σ и у линейная, нормальные напряжения прямо пропорциональны расстоянию слоя волокон от нейтральной оси, совпадающей с главной центральной осью инерции Z.

Вычислим максимальные нормальные напряжения в двутавровом сечении балки

Минимальные (сжимающие) напряжения в двутавровом сечении по абсолютной величине будут равны максимальным растягивающим напряжениям.

Для чугунной балки величина максимальных (растягивающих) напряжений

Минимальные (сжимающие) напряжения

Выбрав масштаб, строим эпюры распределения нормальных напряжений по высоте стальной (рис.27, а) и чугунной (рис.27, б) балок.

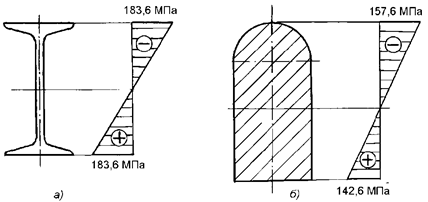
Рис. 27. Распределение нормальных напряжений по высоте балок

Пример 5.

Подобрать из расчета на прочность и жесткость прямоугольное h=2b, круглое и двутавровое поперечные сечения балки, расчетная схема которой показана на рис. 28, а.

Дано: F=5 кН; M=24 кНм; q=30 кН/м; L=4 м; [V]=l/200; [σ]=240 Мпа; E=2,06∙10⁵ Мпа.

Рис. 28

Решение.

1. Построение эпюр внутренних усилий

Из условия равновесия балки, взяв сумму моментов относительно точек а и b, находим реакции в опорах: R_a=8,5 кН, R_b=101,5 кН.

Применяя метод сечений, находим значения изгибающего момента M_Z и поперечной силы Q в сечениях балки. По найденным значениям строим эпюры Q и M_Z (рис. 28, б, в).

2. Определение размеров поперечного сечения балки W_z из условия прочности

По эпюре находим наибольший изгибающий момент, возникающий в сечениях балки M_zmax=50 кНм. Используя условие прочности, определяем момент сопротивления:

Определив W_z, находим размеры поперечного сечения.

а) Прямоугольное сечение.

Момент сопротивления прямоугольного сечения определяется по формуле

где h=2b.

Следовательно,

Отсюда

Площадь прямоугольного сечения равна A=h∙b=92,48 см².

б) Круглое сечение.

Момент сопротивления круглого сечения определяется по формуле

Тогда

отсюда

Площадь круглого сечения

в) Двутавровое сечение.

По таблице сортамента (ГОСТ 8239-72*) подбираем двутавр (W_z ≥ 208,3 см³) № 22 с моментом сопротивления W_z= 232 см³ и площадью сечения A=30,6 см².

Сравнив площади поперечных сечений, можно сделать вывод, что наиболее рациональным является двутавровое поперечное сечение.

3. Построение эпюр прогибов и углов поворота

Для построения эпюр прогибов и углов поворота используем универсальные уравнения прогибов

и углов поворота

метода начальных параметров.

На рис. 28, г приведена расчетная схема.

Начальные параметры равны: Q₀=R_a=8,5 кН; M₀=0; V₀=0; φ₀≠0.

Неизвестным начальным параметром является φ₀. Для определения φ₀ составим уравнение прогибов в сечении на правой опоре, учитывая, что здесь V_b=0.

Подставив значения, получим

В результате получим рад.

Для построения эпюр прогибов и углов поворота разобьем пролет балки на четыре части, а консоль на две.

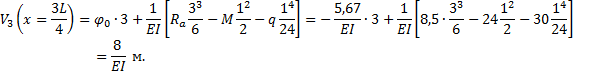
Вычисленные результаты сводим в таблицу.

Значения прогибов и углов поворота балки

x	0				l
V, м	0				0
φ, рад

По данным этой таблицы строим эпюры прогибов и углов поворота балки (см. рис.28, д, е).

4. Определение размеров поперечного сечения балки из условия жесткости

По эпюре прогибов определяем наибольший прогиб, который равен , где J_Z – момент инерции балки относительно оси Z.

Используя условие жесткости балки V_max≤[V],

найдем

По условию задачи

а) Прямоугольное сечение:

Отсюда h=2b=23,1 см.

Площадь прямоугольного сечения равна A=h∙b=273,705 см².

б) Круглое сечение:

Отсюда

Площадь круглого сечения

в) Двутавровое сечение.

По таблице сортамента (ГОСТ 8239-72*) подбираем двутавр (Jz≥1028 см⁴) № 18 с моментом сопротивления J_z=1290 см⁴ и площадью сечения A=23,4 см².

Таким образом, сравнивая все полученные сечения, окончательно принимаем двутавр №22 как наиболее рациональное сечение, обеспечивающее выполнение условий прочности и жесткости.

Пример 6.

Для балки, изображенной на рис. 29, а, требуется:

1) построить эпюры поперечных сил Q_y и изгибающих моментов M_x, найти ;

2) подобрать прямоугольное (h:b=2), кольцевое (d_внутр:d_внеш=0,8) и двутавровое поперечное сечение при [σ]=160 Мпа;

3) выбрать наиболее рациональное сечение по расходу материала.

Для деревянной балки круглого поперечного сечения (рис. 29, б) требуется:

1) построить эпюры Q_y и M_x, найти ;

2) подобрать диаметр сечения при [σ]=8 Мпа;

3) построить эпюру прогибов при E=12 Гпа (по 3 ординатам на каждом участке).

Дано: l₁=1,8 м, l₂=6 м, a₁/a=7, a₂/a=8, a₃/a=1, M=7 кНм, F=8 кН, q=6 кН/м.

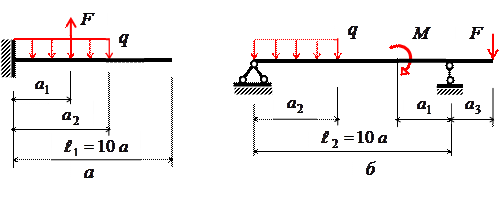
Рис. 29

Решение.

Задача 1 (рис.29,а)

В нашем случае l₁=1,8 м=10а, следовательно a=0,18 м. При этом a₁=7a=1,26 м, a₂=8a=1,44 м. Расчетная схема балки, соответствующая исходным данным, показана на рис. 30.

Приложенные к балке два вида нагрузок разделяют ее длину на три участка и вызывают в защемлении опорную реакцию R₀ и опорный момент M₀. Определяем их значения, используя условия равновесия сил, действующих на консоль (рис. 30):

ΣF_y=0, R₀+8-6∙1,44=0, R₀=0,64 кН;

Σm₀=0, M₀-8∙1,26-6∙1,44∙0,72=0, M₀=3,86 кНм.

Если опорные реакции R₀ и M₀ найдены верно, то любое другое уравнение равновесия должно тождественно удовлетвориться:

Σm₁=0, M₀+R₀∙1,26-6∙1,44∙0,54=0, 0=0.

Для определения Q_y и M_x на участках балки методом сечений воспользуемся скользящей системой координат. Напомним, что положительный изгибающий момент растягивает нижние волокна и ординаты эп.M_x откладывается на них. Положительная поперечная сила вращает оставленную часть консоли по часовой стрелке и ординаты эп.Q_y откладываются вверх от оси эпюры

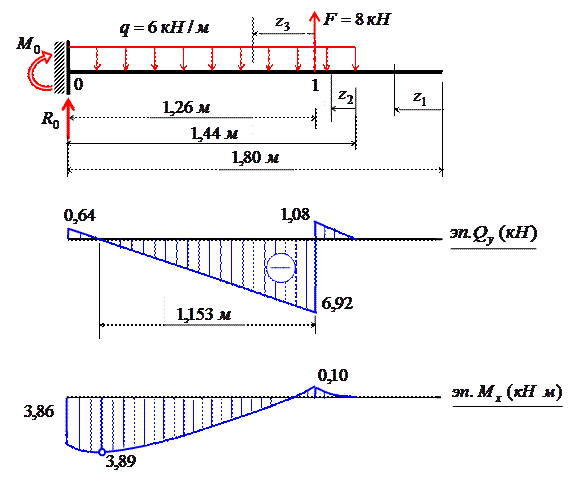
Рис. 30

Итак имеем:

участок № 1 (0≤z₁≤0,36 м) Q₁=0, M₁=0;

участок № 2 (0≤z₂≤0,18 м) Q₂=6z₂, Q₂(0,18)=1,08 кН, M₂(0,18)=0,10 кНм;

участок № 3 (0≤z₃≤1,26м), Q₃==-8+6∙(0,18+z₃)=-6,92+6∙z₃,

Q₃=0, -6,92+6∙=0,

при =1,153 м, Q₃(1,26)=0,64 кН,

M₃(1,153)=3,89 кНм;

M₃(1,26)=3,86 кНм.

Так как между Q_y и M_x существует дифференциальная зависимость (), то если в сечении поперечная сила Q_y=0, то изгибающий момент M_x в этом сечении принимает экстремальное значение.

По эпюре M_x устанавливаем опасное сечение и значение расчетного момента в нем (M_max=3,89 кНм).

Рис. 31

Записываем условие прочности по нормальным напряжениям и определяем требуемое численное значение осевого момента сопротивления W_x:

Рассмотрим прямоугольное сечение (рис. 31). Осевой момент сопротивления будет равен (h=2b):

отсюда b=3,3∙10^-2 м, A=b∙h=2b²=22∙10^-4 м².

Рассмотрим кольцевое сечение (рис. 31). Осевой момент сопротивления будет равен:

отсюда d=7,5∙10^-2 м. Тогда

Рассмотрим двутавровое сечение (рис. 31). По сортаменту ближайшее большее значение W_x будет у двутавра №10 с W_x=39,7 см³=39,7∙10^-6 м³ и площадью поперечного сечения A=12 см²=12∙10^-4 м².

Самым экономичным с точки зрения расхода материала будет двутавровое сечение, так как у него площадь поперечного сечения оказалась наименьшей.

Задача 2 (рис.29,б)

В нашем случае l₂=6 м=10a, следовательно a=0,6 м. При этом a₁=7a=4,2 м, a₂=8a=4,8 м, a₃=a=0,6 м. Расчетная схема деревянной балки, соответствующая исходным данным, показана на рис. 32.

Рис. 32

Приложенные к балке три вида нагрузок разделяют ее длину на четыре участка (0-1, 1-2, 2-3, 3-4) и вызывают в опорах балки реакции H₀, R₀ и R₃, которые определяем из следующих уравнений равновесия:

ΣF_z=0, H₀=0;

ΣM₃=0, 6R₀+10∙0,6+4-6∙6∙3=0, R₀=15,31 кН;

ΣM₀=0, 6R₃-10∙6,6-4-6∙6∙3=0, R₃=21,49 кН;

Проверка: ΣF_y=0, R₀+R₃-8-6∙4,8=0, 0=0.

Определим на участках балки Q_y и M_x:

участок № 1 (0≤z₁≤0,18 м), Q₁=15,31-6∙z₁, M₁==15,31∙z₁-6∙ Q₁=0, при =2,55 м; Q₁(1,8)=4,51 кН; M₁(1,8)=17,84 кНм;

участок № 2 (0≤z₂≤0,6 м), Q₂=8 кН, M₂=-8∙z₁, M₂(0,6)=-4,8 кНм;

участок № 3 (0≤z₃≤1,2 м), M₃=21,49∙z₃-8∙(z₃+0,6)=13,49∙z₃-4,8; Q₃=8-21,49=13,49 кН; M₃(1,2)=11,38 кНм;

участок № 4 (0≤z₄≤3 м), Q₄=15,31-6∙(z₄+1,8)=4,51-6∙z₄, Q4=0 при =0,75 м; Q₄(3,0)=-13,49 кН;

M₄(0)=15,31∙(z₄+1,8)+7-6∙ , M4(0)=24,84 кНм; M₄(0,75)=26,54 кНм, M₄(3,0)=11,38 кНм.

По полученным в характерных сечениях значениям Q_y и M_x строим эпюры Q_y и M_x (рис. 32). По эпюре M_x устанавливаем опасное сечение и значение расчетного момента в нем (M_max=26,54 кНм).

Искомый диаметр балки находим из условия прочности по нормальным напряжениям:

Прогибы характерных сечений деревянной балки определим методом начальных параметров. Начало координат совмещаем с левым крайним сечением балки (рис. 33). По условию задачи начальный прогиб v₀ равен нулю (v₀=0). Уравнение метода начальных параметров на различных участках принимает следующий вид:

на первом участке (0≤z₁≤0,18 м)

на втором участке (1,8≤z₂≤4,8 м)

на третьем участке (4,8≤z₃≤6,0 м)

на четвертом участке (6,0≤z₄≤6,6 м)

Рис. 33

Второй начальный параметр (начальный угол поворота φ₀) найдем из граничного условия, которое говорит, что при z₃=6 м, прогиб опорного сечения 3 равен нулю v_y(6)=0:

Вычислим прогиб посередине второго участка:

Остальные прогибы по краям и посередине всех четырех участков вычисляем аналогичным способом. Эпюра прогибов приведена на рис. 33.

Пример 7.

Для консольной балки, изображенной на рис.34 и двухопорной балки, изображенной на рис.35 требуется:

1. Построить эпюры поперечных сил Q и изгибающих моментов M_z.

2. Подобрать из условия прочности сечения для консольной балки в виде двутавра, а для балки на двух опорах в соответствии с рис.36.

3. Определить перемещение свободного конца консольной балки.

Дано: Материал балки сталь Ст3; Е = 2∙10⁵ МПа; [σ] = 160 Мпа, а₁=1 м; а₂ = 4 м; а₃ = 1 м; а₄ = 2 м; а₅ = 2 м; а₆ = 2 м; q = 10 кН/м; F = 30 кН; М = - 40 кНм;

Решение.

1) Консольная балка (рис.34)

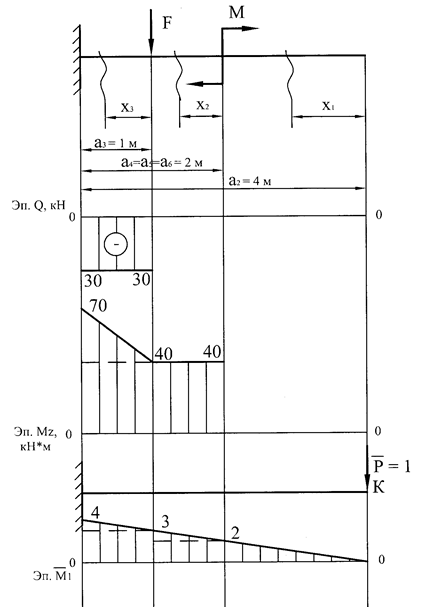
Рис.34

1. Построение эпюр Q и М_я

Участок 1

Q₁ = 0; M_z1 = 0

Участок 2

Q₂ = 0;

ΣM_{z сеч.Х2} = 0; М_z2 +M = 0

M_z2 = - M = - 40 кНм

Участок 3

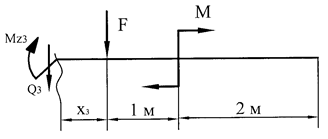
ΣY = 0; -Q₃ - F = 0

Q₃ = - F = - 30 кН

ΣМ_{z сеч.Х3} = 0;

М_z3 = M + F∙x₃ = 0; M_z3 = - M - F∙x₃

x₃ = 0 M₃ = - 40 кНм;

х₃ = 1 м М₃ = - 40 - 30∙1 = - 70 кНм

Строим эпюры Q и M_z (рис.34).

2. Определение сечения балки

Опасное сечение балки в заделке. Условие прочности

Подбираем двутавр №30 с W_I = 472 см³; I_I = 7080 см⁴.

3.Определение перемещения конца балки.

Прикладываем в точке К единичную силу и строим единичную эпюру изгибающего момента .

Прогиб конца балки равен

Конец балки прогибается вниз.

2) Двухопорная балка (рис.35)

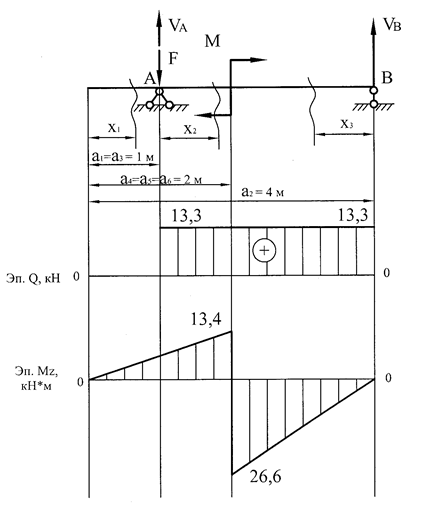
Рис.35

1. Определение опорных реакций.

ΣМ_В = 0; V_A ∙3 - F∙3 + M = 0;

ΣМ_А = 0; V_В∙3 - M = 0;

2. Определение Q и М_z

Участок 1

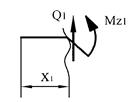
Q₁ = 0; M_z1 = 0

Участок 2

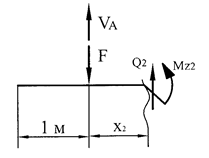
ΣY=0; Q₂ - F + V_A = 0;

Q₂ = F – V_A = 30 – 16,7 = 13,3 кН

ΣМ_{z сеч X2} = 0;

M_z2 + (F - V_A)∙x₂ = 0;

М_z2 = - (F - V_A)∙x₂

x₂ = 0 M_z2 = 0;

x₂ = 1 м М_z2 = (30 – 16,7)∙1 = 13 кНм.

Участок 3

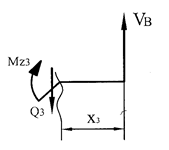
ΣY=0; -Q₃ + V_В = 0; Q₃ = V_В = 13,3 кН

ΣМ_{z сеч X3} = 0; M_z3 – V_В∙x₃ = 0; М_я3 = V_В∙x₃

x₃ = 0 M_z3 = 0;

x₃ = 4 м М_z3 = 13,3∙2 = 26,6 кНм.

Строим эпюры Q и М_z (рис.35).

3. Определение геометрических характеристик сечения балки

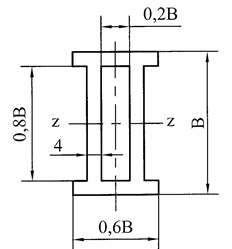
Рис.36

Момент инерции сечения

Момент сопротивления сечения

4. Определение размеров сечения балки

Опасное сечение под сосредоточенным моментом. Условие прочности имеет вид

Пример 8.

Для консольной балки, изображенной на рис.37 требуется:

1. Построить эпюры поперечных сил и изгибающих моментов

2. Подобрать деревянную балку круглого поперечного сечения из условия прочности по нормальным напряжениям.

Дано:

Рис.37

Решение.

1. Разделим балку на 3 участка. Для каждого участка запишем аналитические выражения для поперечных сил и изгибающих моментов

По полученным результатам построим эпюры поперечных сил и изгибающих моментов

Эпюра

Эпюра

Рис.38

Из построенной эпюры видно, что опасным будет сечение на втором участке , в котором изгибающий момент достигает значения

2. Подбираем деревянную балку круглого поперечного сечения из условия прочности по нормальным напряжениям. Условие прочности:

где – момент сопротивления круглого поперечного сечения при изгибе.

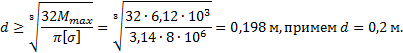
Пример 9.

Для шарнирно-опертой балки, изображенной на рис.39 требуется:

1. Построить эпюры поперечных сил и изгибающих моментов

2. Подобрать стальную балку двутаврового поперечного сечения из условия прочности по нормальным напряжениям.

Дано:

Рис.39

Решение.

1. Прежде чем записать аналитические выражения для поперечных сил и изгибающих моментов необходимо вначале определить опорные реакции.

Следовательно, опорные реакции определены правильно.

Разобьем балку на четыре участка и для каждого запишем аналитические выражения для поперечных сил и изгибающих моментов

т.к. поперечная сила на участке меняет знак, необходимо функцию исследовать на экстремум:

По полученным результатам построим эпюры поперечных сил и изгибающих моментов (рис.40)

Эпюра

Эпюра

Рис.40

Из построенной эпюры видно, что опасным будет сечение на втором участке , в котором изгибающий момент достигает значения

2. Подбираем стальную балку двутаврового поперечного сечения условия прочности по нормальным напряжениям. Условие прочности:

Из сортамента ГОСТ 8239-89 находим ближайшее значение , что соответствует двутавру №16.

Пример 10.

Для стальной шарнирно-опертой двутавровой балки (рис.41) требуется:

1) подобрать поперечное сечение балки двутаврового профиля, исходя из условия прочности,

2) определить ее изогнутую ось.

Дано: М₁ = 60 кНм; М₂ = 0 кНм; q₁ = -30 кН/м; q₂ = -30 кН/м; l₁ = 2,2 м; l₂ = 2,9 м; l₃ = 1,6 м; P = 20 кН; материал-сталь; [σ]=160 МПа; [τ]=96 МПа Е=2∙10⁵ Мпа.

Рис.41

Решение.

Первым шагом расчета является определение реакций для последующего построения эпюр Q и M. Из уравнения статики:

Реакцию найдем из уравнения:

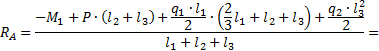
Проверим правильность нахождения реакций, спроектировав все силы на ось :

Из уравнения следует, что реакции опор определены, верно.

Теперь перейдем к составлению аналитических выражений для поперечных сил и изгибающих моментов по участкам балки. При этом заметим, что при составлении уравнений Q и в особенности для M первого участка целесообразнее составлять, отсекая правую часть балки, поэтому начнем рассматривать балку с правой стороны.

участок III:

участок II:

участок I: прежде чем рассмотрим I участок, запишем выражение для ординаты интенсивности нагрузки в произвольном сечении , учитывая, что отсчитывается с правого конца участка. Из подобия треугольников имеем:

Располагая выражениями для Q и M, построим их эпюры.

Подберем профиль двутавра, исходя из условия прочности по нормальным напряжениям:

По сортаменту прокатного профиля выберем двутавр №36 с и проверим прочность балки по касательным напряжениям где

Как видно условие прочности по касательным напряжениям тоже удовлетворяется.

Произведем проверку прочности балки по третьей гипотезе прочности. Для этого построим эпюры Q и для расчетного сечения А (рис.42) т.к. там максимальная поперечная нагрузка.

Рис.42

Основными точками расчетного сечения будут точки 1, 2 и 3, но в точках 1 и 3 прочность уже проверена по и , поэтому осталось проверить прочность в точки 2. Для этого вычислим величины и по формулам:

Подставляя значения и в формулу для приведенных напряжений по третьей гипотезе прочности и сопоставляя с допускаемыми напряжениями , получим:

Следовательно, прочность балки обеспечена.

Теперь перейдем к определению изогнутой оси балки с помощью метода начальных параметров. Для этого рассмотрим произвольное сечение вблизи правого конца балки и запишем дифференциальное уравнение изогнутой оси в соответствии с методом начальных параметров:

После двукратного интегрирования и раскрытия скобок получим:

где C и D постоянные интегрирования, определяемые из граничных условий.

Граничные условия для балки правой опоры записываются как:

y=0 при x=0 тогда

Граничные условия для балки левой опоры записываются как:

y=0 при x=6,7 тогда

Подставляя значения C и D вычислим ординаты изогнутой оси при значениях x=0; x=0,8; x=1,6; x=3,05; x=4,5; x=5,6; x=6,7.

По полученным данным строим ось балки (рис.43).

Рис.43

Пример 11.

Для заданной схемы балки (рис.44, а) требуется:

1) построить эпюру поперечных сил и эпюру изгибающих моментов;

2) из условия прочности подобрать стальную двутавровую балку с указанием её номера по ГОСТ 8239-72.

Допускаемое напряжение на изгиб принять [σ]=150 МПа.

Рис.44

Решение.

Прежде чем приступить к построению эпюр, необходимо определить реакции опор балки. Для этого составим уравнение равновесия:

ΣM_A=0; q∙4∙2 - F∙5 - R_B∙6 + M =0

Отсюда

ΣM_B=0; R_A∙6 - q∙4∙4 + F∙1 + M =0

Отсюда

В данном случае нагружения балки, когда внешние силы, перпендикулярные продольной оси балки и внешние моменты приложены в главной центральной плоскости инерции, в поперечных сечениях возникают два внутренних усилия: поперечная сила Q_y и изгибающий момент М_х (плоский поперечный изгиб).

Обозначим характерные точки балки: А, 1, 2, В, 3 (рис.44, а). Найдём поперечную силу в точке А, где приложена реакция опоры R_А=50 kH, стремящаяся повернуть левую часть балки по часовой стрелке, тогда Q_yA=R_A=50 кН положительна и должна быть отложена в выбранном масштабе вверх от базовой оси, проведённой параллельно оси балки (рис.44, б).

Для определения поперечной силы в точке 1 оставим часть балки, лежащую левее сечения, проведённого через точку 1, а всё, что лежит правее, мысленно отбросим. Сила R_A по-прежнему стремится повернуть левую часть балки по часовой стрелке, следовательно, по принятому правилу знаков, вызовет появление положительной поперечной силы, а равномерно распределённая нагрузка стремится повернуть левую часть балки против часовой стрелки и значит, она вызовет возникновение отрицательной поперечной силы. Найдём алгебраическую сумму этих сил для определения Q_y]=R_A-q∙4=50-20∙4= - 30 кН. Поперечная сила Q_y1 отрицательна, поэтому должна быть отложена в выбранном масштабе ниже базовой линии. На участке А-1 эпюра изобразится наклонной прямой (рис.44, б).

Определяя Q_y2, отбросим правую часть балки и оставим часть балки, лежащую левее точки 2: Q_y2=R_A - q∙4 = -30 кН. Отложим найденное значение в точке 2 на эпюре Q_y ниже базовой линии. На участке 1-2, где нет распределённой нагрузки, эпюра изобразилась прямой, параллельной оси балки. Но, кроме того, в точке 2 приложена сосредоточенная сила F, поэтому она должна быть отложена на эпюре в виде скачка вверх, т.к. стремится повернуть левую часть балки по часовой стрелке.

Поперечную силу в точках В и 3 удобнее определить, отбрасывая часть балки, лежащую левее точек В и 3, и оставляя всё, что лежит правее. Иначе говоря, построить эпюру справа налево. Правее точки В приложен в точке 3 только сосредоточенный момент, который не создаёт поперечной силы: Q_y3=0. Поэтому на участке B-3 эпюра изобразится прямой, совпадающей с базовой линией.

В точке В приложена сосредоточенная сила R_B, поэтому её необходимо отложить в виде скачка. Сила R_B стремится повернуть правую часть балки против часовой стрелки, значит, вызовет возникновение, отрицательной поперечной силы и её нужно отложить вниз Q_yB=R_B = -20 кН. Теперь можно соединить прямой точки эпюры на участке 2-В. Эпюра изобразится в виде прямой, параллельной оси балки. Эпюра Q_y построена.

На участке А-1 наклонная эпюра пересекает нулевую (базовую) ось. В соответствии с ранее записанными правилами на эпюре М_х в этой точке пересечения будет точка перегиба. Найдём значение координаты z . Из подобия треугольников на эпюре Q_y:

Решая полученную пропорцию, получим z=2,5 м. Обозначим на балке эту точку буквой К.

Приступим к построению эпюры изгибающих моментов М_х (рис.44, в).

В точке А (конец балки) изгибающий момент М_xА=0.

Найдём значение изгибающего момента в точке К, отбросив часть балки правее точки К и оставив часть балки левее. Считаем, что в точке балка К закреплена. Реакция опоры R_A изгибает балку сжатыми волокнами вверх, а распределённая нагрузка - вниз, тогда

Отложим на эпюре М_х полученное значение в выбранном масштабе.

Вычислим изгибающий момент в точке 1, по-прежнему оставляя левую часть балки:

M_x1= R_A∙4 - q∙4∙2 = 50∙4 - 20∙4∙2 = 40 кНм.

Отложим это значение на эпюре М_х. Соединим эпюру по найденным точкам параболой, направленной выпуклостью навстречу стрелкам равномерно распределённой нагрузки q.

Чтобы вычислить значение изгибающего момента в точке 2 опять оставим левую часть балки:

M_x2= R_A∙5 - q∙4∙3 = 50∙5 - 20∙4∙3 = 10 кНм.

Отложим это значение на эпюре М_х и соединим с предыдущей точкой эпюры наклонной прямой, плавно сопрягая её с параболической частью эпюры М_х.

Изгибающий момент в точках B и 3 удобнее вычислять, отбрасывая часть балки, лежащую левее этих точек.

В точке 3 приложен сосредоточенный момент М. Отложим на эпюре изгибающих моментов значение М_х3= -М= -10 кНм ниже линии нулей в виде скачка (сжатые волокна находятся внизу). На участке B-3 эпюра изобразится прямой, параллельной базовой линии, так как на правую часть балки до точки В действует только сосредоточенный момент и М_хB= -М= -10 кНм. Соединим значение М_xB с предыдущей точкой М_х2 наклонной прямой. В точке 2 на эпюре моментов, где на балку действует сосредоточенная сила F, получился излом. В точке В на эпюре также получился излом, так как в этой точке на балку действует сосредоточенная сила R_B. Эпюра М_х построена.

Опасным будет сечение, в котором изгибающий момент М_х имеет максимальное значение - в точке К:

max M_x =M_xK= 62,5 кНм.

Из условия прочности:

Из таблицы сортамента прокатных профилей (ГОСТ 8239-72) выбираем

двутавр №27а, для которого W_x=407 см³.

Балка будет перегружена на 2,3%, что допускается, так как перенапряжение допускается ∆=5%.

Онлайн-калькулятор "Подбор круглого сечения балки при изгибе"

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00