Главная

 

Задача 1. Расчет двухопорной балки при действии вынужденных колебаний.   

          На стальной балке (рис.1), установлен электродвигатель весом G, совершающий n об/мин. Центробежная сила, возникающая вследствие неуравновешенности частей двигателя составляет F =0,2G. Подобрать двутавровое поперечное сечение балки из условия отстройки от резонанса ω=1,4φ, определить максимальный прогиб и максимальные напряжения. Собственный вес балки не учитывается.

          Данные взять из табл.1.

Таблица 1

 

1 схема                                               2 схема

                

 

3 схема                                               4 схема

                 

 

5 схема                                               6 схема

                  

 

7 схема                                               8 схема

                  

 

9 схема                                               10 схема

               

 

11 схема                                               12 схема

                  

 

13 схема                                               14 схема

                     

 

15 схема                                               16 схема

                   

 

17 схема                                               18 схема

                     

 

19 схема                                               20 схема

                 

 

21 схема                                               22 схема

                      

 

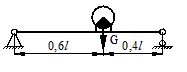
23 схема                                               24 схема

                         

 

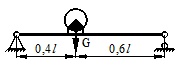
25 схема                                               26 схема

                        

 

27 схема                                               28 схема

                     

 

29 схема                                               30 схема

                      

 

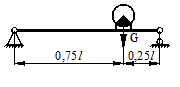
31 схема                                               32 схема

                         

 

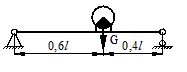
33 схема                                               34 схема

                       

 

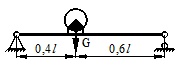
35 схема                                               36 схема

                          

Рис.1

 

 

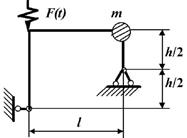
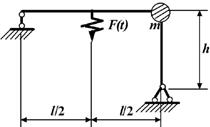
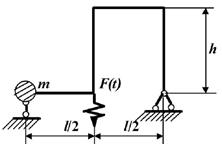
Задача 2. Вынужденные колебания системы с одной степенью свободы.

Исходные данные к задаче принимаются по табл. 2 и схемам на рис. 2

1. Определите круговую частоту свободных колебаний системы, предварительно выяснив направление возможных перемещений сосредоточенной массы.

2. Постройте эпюру изгибающих моментов от статического действия амплитудного значения заданной нагрузки F(t).

3. Вычислите величину перемещения сосредоточенной массы от статического действия амплитуды F(t).

4. Определите амплитудное значение силы инерции, действующей на сосредоточенную массу в процессе вынужденных колебаний, принимая их частоту θ в зависимости от частоты свободных колебаний ω по табл. 2.

5. Постройте эпюру изгибающих моментов от динамического действия нагрузки.

Таблица 2

 

1 схема                                            2 схема

     

 

 

3 схема                                                  4 схема

  

 

 

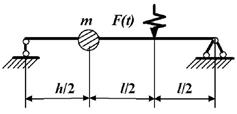
5 схема                                                  6 схема

  

 

 

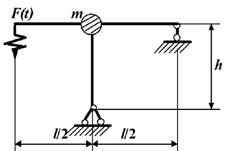
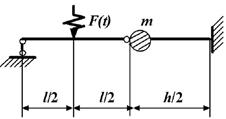
7 схема                                                   8 схема

  

 

 

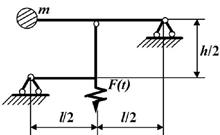
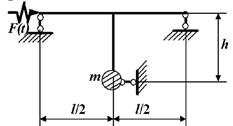
9 схема                                             10 схема

        

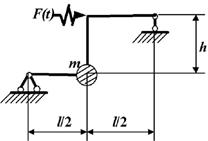
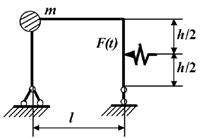
Рис. 2

 

 

Примеры выполнения задач

Пример 1

На двухопорной балке (двутавр №36; погонная масса ­q­ = 46,8 кг/м; I_x = 13380 см⁴; W_x = 743 см³; модуль Юнга E = 2∙10⁵ МПа = 2∙10⁴ кН/см²) посередине пролета установлен электромотор массой М = 3568 кг (рис. 3). В связи с несовпадением оси вращения ротора с его центральной осью образовался эксцентриситет е = 0,25 см, что создает из-за динамической неуравновешенности последнего вибрационную нагрузку на балку. Масса неуравновешенной части ротора m = 698,6 кг, а число оборотов его n = 550 об/мин. Требуется проверить эту систему на резонанс, а также прочность балки при [σ] = 120 МПа (при переменных напряжениях, возникающих в элементах конструкции при колебаниях, допускаемые напряжения понижают).

Рис. 3. К расчету балки на колебания: а – заданная балка;

б – расчетная схема и ее грузовое состояние; в – единичное состояние

Решение.

1. Пренебрегая массой балки (считая ее невесомой), устанавливаем, что такая система обладает одной степенью свободы, ибо положение массы М при вертикальных колебаниях балки определяется одной координатой – прогибом ее в точке крепления электромотора (т. е. посередине пролета).

2. Проверка на резонанс. Для этого надо вычислить статический прогиб балки ∆_ст в точке K (рис. 3,а). Используем метод Мора в форме Верещагина. Сначала строим эпюру изгибающих моментов грузового состояния от действия веса Q (рис. 3, б), потом эпюру единичного состояния (рис. 3, в). По участкам вычисляем площади Ω_i грузовой эпюры и определяем положение центров их тяжести.

Под центрами тяжести площадей Ω_i в эпюре  определяем ординаты . Тогда  где в силу симметрии имеем   так что

Изгибная жесткость стальной балки в данном случае EI_x = 2∙10⁴ кН/см² ∙13380 см⁴ = 2,776∙10⁸ кНсм² и, следовательно, при Q = M∙g = 3568 кг∙9,81 м/с² = 35000 Н = 35 кН.

Круговая частота собственных колебаний системы

Частота вынужденных колебаний (при n = 560 об/мин)

Отношение частот вынужденных и собственных колебаний

Это означает, что система вошла в запретную зону резонансов. Как быть? Конструктор может заменить материал балки (что проблематично), изменить место крепления груза на балке (что чаще всего не допускается), изменить жесткость балки, т. е. принять балку иного сечения. Последнее чаще всего и делается.

Изменим сечение, приняв двутавр № 40 (I_x = 19062 см⁴; W_x = 953 см³).

Тогда

а круговая частота собственных колебаний системы

отношение частот вынужденных и собственных колебаний

Из зоны резонансов вышли.

3. Проверка прочности балки:

где  (отношение статических прогибов здесь вполне можно заменить отношением сил, их вызвавших, ибо в линейно деформируемых системах перемещения ∆ пропорциональны силам). Центробежная сила инерции  равномерно вращающейся массы m = 698,6 кг равна  В свою очередь коэффициент нарастания колебаний

так что

Тогда

Прочность балки обеспечена.

 

 

Пример 2

Медный стержень круглого поперечного сечения диаметром d = 2,5 см и длиной R₀ = 3 м (рис. 4) удерживает на нижнем торце груз массой M = 3920 кг. Пренебрегая массой стержня, определить частоту и период собственных колебаний этой упругой системы.

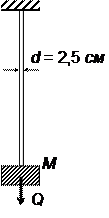
Рис.4

Решение.

1. Эта система (см. рис. 4, а) обладает одной степенью свободы.

2. Круговая частота ω собственных колебаний определится по формуле

где g = 9,81 м/с² = 981 см/с² – ускорение свободного падения; ∆_ст – удлинение стержня от веса Q груза, равного

Q = M∙g = 3920∙9,81 = 38455 Н = 38,455 кН.

Это продольное удлинение в данном случае удобно вычислить по формуле Гука как

где для меди модуль Юнга E_м = 1,1∙10⁵ МПа = 1,1∙10⁴ кН/см², а площадь поперечного сечения

Таким образом,

Тогда круговая частота собственных колебаний

период колебаний

техническая частота

минутная частота

3. Если при прочих равных условиях взять стержень алюминиевый (E_ал = 0,7∙10⁵ МПа = 0,7∙10⁴ кН/см²), то

и круговая частота

а период колебаний

Как видно, частота ω и период T зависят не только от расчетной схемы и геометрических характеристик сечений элементов, но и от упругих свойств материала конструкции (от модуля Юнга E).

4. Оценим, насколько оправдано пренебрежение массой стержня при вычислении ω и T. Плотность меди ρ_м = 8960 кг/м³ = 8,96 г/см³, так что масса рассмотренного выше стержня (V₀=R₀A₀  – объем) m_м = ρ_мV₀ = = 8,96∙3∙10²∙4,9∙10 ^–3 = 13,17 кг и это составляет 1/297 часть от массы груза. Для алюминиевого стержня, при плотности ρ_ал = 2,7 г/см³, это составляет 1/987 часть от массы груза M. В данном случае пренебрежение массой стержня – оправдано.

 

 

Пример 3

На консольной балке (рис.5), состоящей из двух швеллеров № 12 установлен агрегат весом G = 4 кН, создающий вибрационную нагрузку F = F_o∙sinΩt, при этом F_o=1 кН,  Ω= 22 с^-1.

Определить величину динамического коэффициента. В случае попадания в зону критических частот добиться, чтобы χ≤2 и определить величину максимальных и минимальных нормальных напряжений. Весом балки и внутренним трением пренебречь.

Рис.5

Решение.

По ГОСТ 8240-89 для швеллера № 12: I_z=304 см⁴, W_z=50,6 см², тогда для сечения, состоящего из двух швеллеров I_z= 2∙304 = 608 см⁴,   W_z=2∙50,6= 101,2 см³.

В случае вынужденных колебаний коэффициент динамичности

Собственная частота колебаний

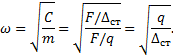
Построив эпюру M_z и  (от единичной силы, приложенной вертикально в сечении А), определим с помощью интегралов Мора (вычисляя способом Верещагина)

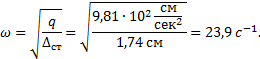
Отличие собственной частоты колебаний ω от частоты вынужденных колебаний Ω – незначительно, поэтому - весьма велик.

Для отстройки от области критических частот изменим l до 2 метров, тогда =0,82 см и соответственно

Опасное сечение – в заделке. Напряжения от веса агрегата

Динамическая составляющая от вибрационной нагрузки

- является амплитудой переменной во времени составляющей напряжений. Следовательно, напряжения изменяются от σ_max = 79,2 + 35,6 = 114,8 МПа до σ_min = 79,2 – 35,6 = 43,6 Мпа (рис.6).

Рис.6

 

---