Расчетно-графические работы

 

 

Главная

 

 

Задача 1. Расчет  плоской балочной фермы с построением линии влияния

Расчет рам и ферм SOPROMATGURU.RU

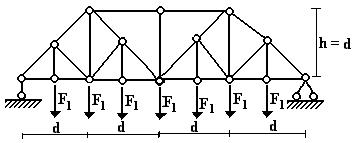
Для одной из балочных ферм, изображенных на рис. 1 требуется:

1) определить аналитически усилия в отмеченных стержнях от неподвижной нагрузки в виде сосредоточенных сил F, приложенных в каждом узле прямолинейного пояса фермы;

2) построить линии влияния усилий для отмеченных стержней при «езде» по прямолинейному поясу фермы;

3) вычислить по линиям влияния усилия в отмеченных стержнях от сил F и результаты сравнить со значениями усилий, полученными аналитически.

Исходные данные для расчета принять из табл.1.

Таблица 1

Номер

строки

Схемы балок

рис. 1

h, м

l, м

F, кН

01

1 

2

2

5

02

2

1,5

1

7

03

3

0,75

1,5

9

04

4

1,75

1,5

10

05

5

2

1

8

06

6

3

2

6

07

7

3

2,5

4

08

8

0,75

1

6

09

9

1,5

1,5

7

10

10

2

2

9

11

11

1

2,5

5

12

12

2

2

4

13

13

1,5

1

6

14

14

1,75

1,5

5

15

15

1

2

10

16

16

2

2,5

8

17

17

2,5

1

5

18

18

1

1,5

5

19

19

1,5

2

8

20

20

0,75

1

9

21

21

1

2,5

9

22

22

2

2

10

23

23

1

1

5

24

24

0,75

2

6

25

25

1

1

7

26

1 

0,75

1

6

27

2

1,5

1,5

7

28

3

2

2

9

29

4

1

2,5

5

30

5

2

2

4

31

6

1,5

1

6

32

7

1,75

1,5

5

33

8

1

2

10

34

9

2

2,5

8

35

10

2,5

1

5

36

11

1

2,5

8

 

в

а

б

г

 

Схема 1                                                         Схема 2

1

 

 

Схема 3                                                         Схема 4

1

 

 

Схема 5                                                         Схема 6

1

 

 

Схема 7                                                         Схема 8

1

 

 

Схема 9                                                         Схема 10

1

 

 

Схема 11                                                         Схема 12

1

 

 

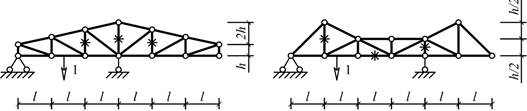
Схема 13                                                         Схема 14

1

 

 

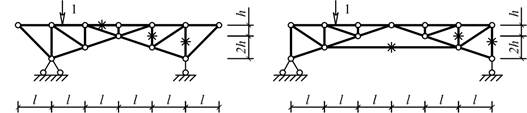
Схема 15                                                         Схема 16

1

 

 

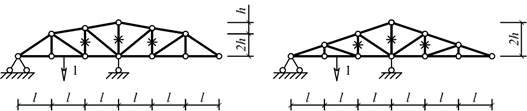
Схема 17                                                         Схема 18

1

 

 

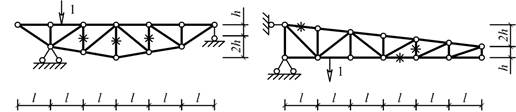
Схема 19                                                         Схема 20

1

 

 

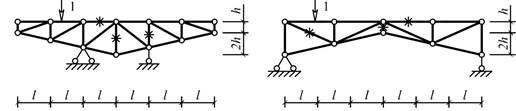
Схема 21                                                         Схема 22

1

 

 

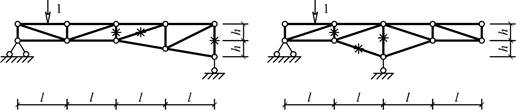
Схема 23                                                         Схема 24

1

 

 

Схема 25

1

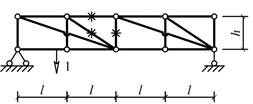
Рис. 1

 

Пример решения задачи

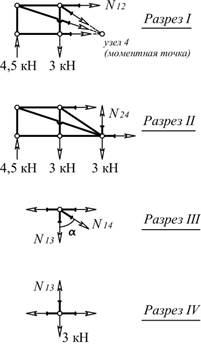
Исходные данные: схема фермы на рис. 2; l=4 м; h=3 м; F=3 кН.

а) Аналитическое определение усилий в отмеченных стержнях от неподвижной нагрузки

 

1

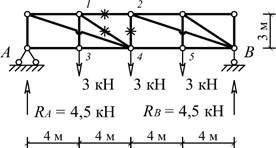
Рис. 2

 

 

1

 

ΣM4=0:  N12∙3+4,5∙8-3∙4=0 ⟹ N12= -8 кН

 

 

 

 

ΣY=0:  N24+4,5-3-3=0 ⟹ N24= 1,5 кН

 

 

 

 

ΣY=0:  -N14∙cosα-N13=0 ⟹ N14= -N13/cosα

 

 

 

 

ΣY=0:  N13-3=0 ⟹ N13=3 кН

N14= -N13/cosα=-3/(3/5)=-5 кН.

 

 

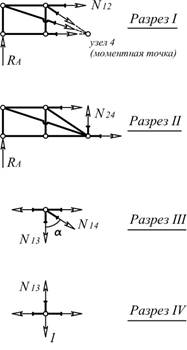
б) Линии влияния усилий для отмеченных на схеме стержней

 

1

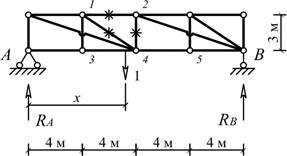
Рис. 3

 

 

1

 

 

ΣM4=0:  N12=-RA∙(8/3) (уравнение правой ветви)

 

 

 

ΣY=0:  N24=-RA (уравнение правой ветви)

 

 

 

 

ΣY=0:  N14=-N13∙(5/3)

 

 

 

ΣY=0:  N13=1

 

 

1

Рис. 4

 

в) Определение усилий в отмеченных стержнях по формуле влияния от сил F=3 кН.

N12=3∙(-2/3)+3∙(-4/3)+3∙(-2/3)=-8 кН,

N24=3∙(1/4)+3∙(1/2)+3∙(-1/4)=1,5 кН,

N13=3∙1=3 кН,

N14=3∙(-5/3)=-5 кН.

 

Пояснения к решению задачи

1) Аналитический способ нахождения усилий от неподвижной нагрузки требует рассмотрения равновесия отсеченной части фермы, содержащей определяемое усилие.

2) Основой для построения линий влияния в стержнях фермы, в большинстве случаев, являются линии влияния опорных реакций, вид и значение ординат которых очевиден. Задача, как правило, сводится к нахождению связи внутреннего усилия с реакциями опор через законы равновесия и последующего перемасштабирования линий влияния реакций. В приведенном примере связь усилия в стержне 1–2 с реакцией RA, когда груз находится справа от разреза I, определена из равенства нулю моментов относительно точки (узла) 4 для левой отсеченной части фермы. В результате получено уравнение правой ветви, а левая ветвь, как известно, пересекается с правой в точке, лежащей на одной вертикали с моментной точкой (узлом) 4. Для усилия в стержне 2–4 ветви линии влияния параллельны, поскольку связь с реакцией определяется уравнением равновесия . Для построения линии влияния усилия в стержне 1–4 использована связь этого усилия с усилием в стержне 1–3 из равновесия узла 1, а линия влияния усилия в стержне 1–3 легко построить, если рассмотреть равновесие узла 3.

 

 

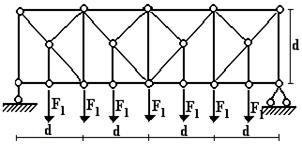
Задача 2. Расчет  плоской балочной фермы при заданной неподвижной нагрузке

При заданной неподвижной нагрузке определить внутренние усилия в стержнях указанной в табл. 2 панели фермы.

Данные взять из табл.2

Таблица 2

Номер

cтроки

Номер схемы

по рис.5

№ панели

фермы

F1,

кН

F,

кН

d,

м

01

1

2

12

8

2

02

2

2

10

16

3

03

3

2

12

4

4

04

4

3

6

10

2

05

5

3

8

4

5

06

6

1

10

4

6

07

7

2

6

3

3

08

8

2

8

10

2

09

9

1

6

8

4

10

10

3

12

6

3

11

11

2

11

8

5

12

12

3

12

16

1

13

13

3

10

4

2

14

14

1

12

10

4

15

15

2

6

4

5

16

16

2

8

4

3

17

17

1

10

3

2

18

18

2

6

10

5

19

19

2

8

8

3

20

20

3

6

8

2

21

21

3

12

16

1

22

22

1

12

4

3

23

23

2

13

10

4

24

24

2

14

4

5

25

25

1

12

4

3

26

26

3

10

3

2

27

27

2

12

10

1

28

28

3

6

8

3

29

29

3

8

6

5

30

30

1

10

8

4

31

31

2

6

16

2

32

32

2

8

5

1

33

33

1

6

10

3

34

34

3

12

6

6

35

35

2

11

8

4

36

36

3

12

6

2

 

г

б

а

г

в

 

1 схема                                                                     2 схема                         

 

 

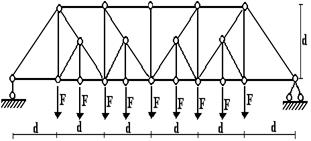
3 схема                                                               4 схема                         

 

 

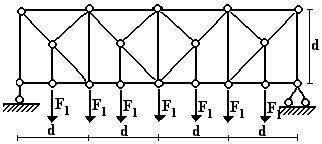
5 схема                                                                  6 схема                         

 

 

7 схема                                                                         8 схема                         

 

 

9 схема                                                                          10 схема                         

 

 

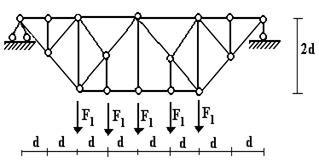
11 схема                                                                        12 схема                         

 

 

13 схема                                                                        14 схема                         

 

 

15 схема                                                          16 схема                         

 

 

17 схема                                                                      18 схема                         

 

 

19 схема                                                                   20 схема                         

 

 

21 схема                                                        22 схема                         

 

 

23 схема                                                                    24 схема                         

 

 

25 схема                                                                        26 схема                         

 

 

27 схема                                                       28 схема                         

 

 

29 схема                                                                30 схема                         

 

 

31 схема                                                                   32 схема                         

 

 

33 схема                                                                    34 схема                         

 

 

35 схема                                                                   36 схема                         

Рис. 5

 

 

Задача 3. Расчет  плоской балочной фермы с построением линий влияния

Для фермы (рис.6) с выбранными из табл.3 размерами и нагрузкой требуется:

1) определить аналитически усилия во всех стержнях фермы;

2) построить линии влияния усилий в стержнях заданной панели, включая правую стойку, от действия подвижной нагрузки;

3) с помощью линий влияния подсчитать значения усилий от заданной нагрузки и сравнить их со значениями, полученными в пункте 1).

 

Таблица 3

Номер

строки

Номер схемы

по рис.6

№ панели

d, м

h, м

Р, кН

01

1

2

3,0

3,0

1,8

02

2

3

4,0

5,5

1,5

03

3

4

2,5

3,5

1,2

04

4

5

3,5

4,0

1,0

05

5

2

4,5

6,0

1,9

06

6

3

3,0

4,2

2,0

07

7

4

2,5

4,6

1,1

08

8

5

4,0

4,5

1,3

09

9

2

3,5

5,0

1,4

10

10

3

4,5

4,4

1,6

11

11

4

2,3

3,2

2,1

12

12

5

2,8

5,2

2,8

13

13

2

4,1

4,4

2,5

14

14

3

2,6

3,4

2,2

15

15

4

3,3

5,4

2,9

16

16

5

4,7

4,3

2,6

17

17

2

3,2

3,6

2,3

18

18

3

3,8

5,6

3,0

19

19

4

2,4

4,1

2,7

20

20

5

3,6

3,8

2,4

21

1

3

3,5

3,0

1,5

22

2

4

4,5

5,5

1,2

23

3

5

3,0

3,5

1,0

24

4

2

2,5

4,0

1,9

25

5

3

4,0

6,0

2,0

26

6

4

3,5

4,2

1,1

27

7

5

4,5

4,6

1,3

28

8

2

2,3

4,5

1,4

29

9

3

2,8

5,0

1,6

30

10

4

4,1

4,4

2,1

31

11

5

2,6

3,2

2,8

32

12

2

3,3

5,2

2,5

33

13

3

4,7

4,4

2,2

34

14

4

3,2

3,4

2,9

35

15

5

3,8

5,2

2,6

36

16

3

2,4

4,4

2,3

 

в

б

а

г

в

 

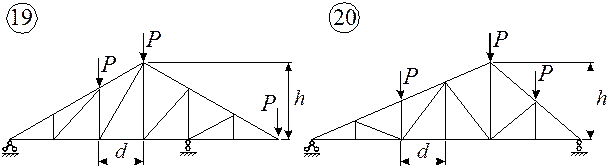
Рис.6

 

Пояснения к решению задачи

Усилие в каждом стержне следует определять непосредственно через нагрузку и опорные реакции, для каждого усилия выбрать оптимальный способ из трех известных (моментной точки; проекций; вырезания узлов).

При определении усилий необходимо показывать используемые сечения, приводить соответствующие уравнения, а все величины, входящие в них, должны быть указаны на чертеже. Геометрические размеры надо определять аналитически.

Построение линий влияния должно сопровождаться необходимыми расчетными формулами. Линии влияния строятся под схемой фермы. На них должны быть проставлены числовые значения ординат под всеми узлами. Для определения усилий в стержнях с помощью линий влияния использовать указания к задаче 1.

 

 

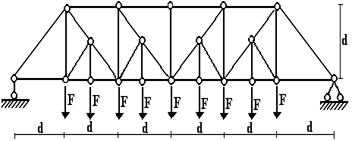
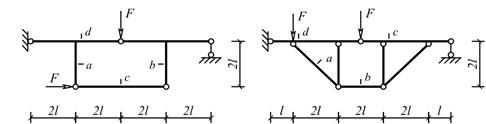
Задача 4. Расчет  плоской балочной фермы с построением линий влияния

Для простой плоской фермы (рис. 7), нагруженной в узлах верхнего пояса сосредоточенными силами F с выбранными из табл. 4 исходными данными требуется:

а) определить (аналитически) усилия в стержнях заданной панели, включая правую стойку (4 стержня);

б) построить линии влияния усилий в тех же стержнях;

в) по линиям влияния подсчитать значения усилий от заданной нагрузки и сравнить со значениями, полученными аналитически.

 

Таблица 4

Номер

cтроки

Номер схемы

по рис.7

№ панели

фермы

l,

кН

F,

кН

h,

м

01

1

2

30

1,8

3,0

02

2

3

28

1,5

5,5

03

3

4

27

1,2

3,5

04

4

5

24

1,0

4,0

05

5

2

21

1,9

6,0

06

6

3

18

2,0

4,2

07

7

4

32

1,1

4,6

08

8

5

33

1,3

4,5

09

9

2

22

1,4

5,0

10

0

3

23

1,6

4,4

11

1

2

30

1,8

3,0

12

2

3

28

1,5

5,5

13

3

4

27

1,2

3,5

14

4

5

24

1,0

4,0

15

5

2

21

1,9

6,0

16

6

3

18

2,0

4,2

17

7

4

32

1,1

4,6

18

8

5

33

1,3

4,5

19

9

2

22

1,4

5,0

20

0

3

23

1,6

4,4

21

1

2

30

1,8

3,0

22

2

3

28

1,5

5,5

23

3

4

27

1,2

3,5

24

4

5

24

1,0

4,0

25

5

2

21

1,9

6,0

26

6

3

18

2,0

4,2

27

7

4

32

1,1

4,6

28

8

5

33

1,3

4,5

29

9

2

22

1,4

5,0

30

0

3

23

1,6

4,4

31

1

2

30

1,8

3,0

32

2

3

28

1,5

5,5

33

3

4

27

1,2

3,5

34

4

5

24

1,0

4,0

35

5

2

21

1,9

6,0

36

6

3

18

2,0

4,2

 

а

б

г

в

б

 

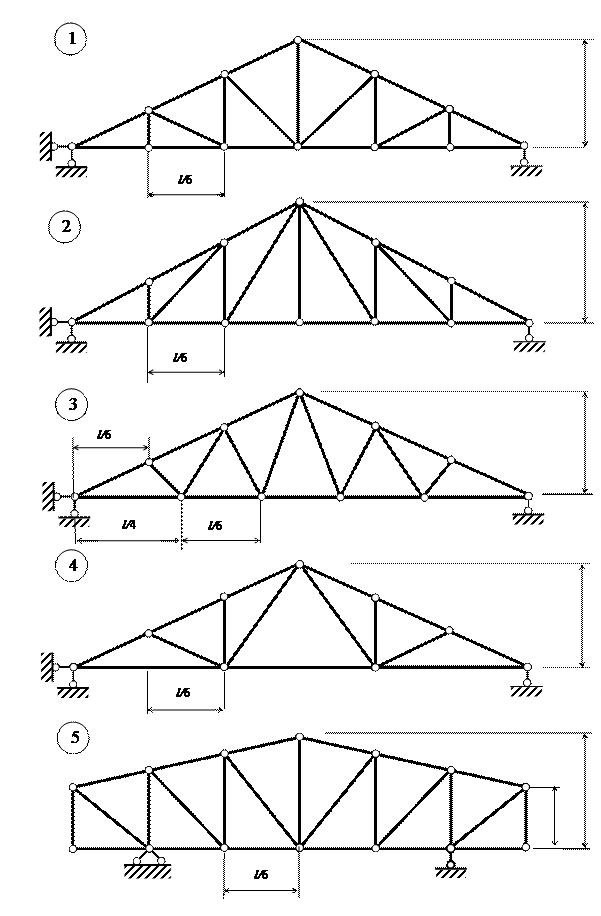
Подпись: hПодпись: h/2 h/2 Подпись: hПодпись: hПодпись: hПодпись: h h h h

Подпись: hПодпись: hПодпись: hПодпись: hПодпись: h/2Подпись: h h h hПодпись: h/2Подпись: h/2Подпись: h/4Подпись: h/2

Рис.7

 

Пояснения к решению задачи

По условию задачи требуется определить усилия не во всех стержнях фермы, а только в стержнях заданной панели. В этом случае удобно воспользоваться способом сквозных сечений.

Сущность способа состоит в следующем: ферму рассекают на две части таким образом, чтобы в разрез попало не более трех стержней  с неизвестными усилиями; одну из частей мысленно отбрасывают, а ее действие на оставшуюся заменяют усилиями. Затем составляют уравнения моментов относительно моментных точек, (находящихся на пересечении двух из трех стержней), или уравнения проекций, если два из пересекаемых стержней параллельны. Таким образом, можно получить три уравнения и в каждом будет по одному неизвестному.

Особенность расчета шпренгельных ферм является то, что для некоторых стержней нельзя провести удачного сечения (пересекающего не более трех стержней). В связи с этим появляется необходимость переходить к схеме взаимодействия шпренгеля с основной решеткой. Для этого необходимо предварительно выделить основную и дополнительную решетки и установить схемы их взаимодействия с основной решеткой, т.е. схемы передачи нагрузки со шпренгелей в узлы основной фермы.

Для успешного расчленения заданной фермы на основную и шпренгель необходимо твердо усвоить типы шпренгелей.

Следует иметь в виду, что в большинстве случаев (для всех заданных ферм) усилия в элементах, входящих и в шпренгель и в основную решетку

удается определить, рассматривая непосредственно заданную ферму. В связи с этим рекомендуется сначала рассмотреть заданную схему и найти  все усилия, для которых возможно провести удачное сечение.

Остальные усилия определяются из рассмотрения только шпренгеля или только основной решетки. При этом в работе обязательно нужно приводить схемы шпренгеля и основной решетки отдельно с указанием узловой нагрузки, полученной в результате передачи местной нагрузки со шпренгеля в узлы основной решетки.

Производя определение усилий, надо приводить все схемы, разрезы и указывать все величины, входящие в расчетные формулы. Геометрические характеристики (плечи, углы и пр.) должны быть определены аналитически, а не графически.

Построение линий влияния усилий в стержнях ферм начинают с построения линий влияния опорных реакций. Для балочных ферм, эти линии влияния имеет такой же вид, как и  линии влияния опорных реакций балок того же пролета. Затем груз F = 1 устанавливается в произвольном узле фермы по одну сторону от сечения (например, слева). Для определения усилия составляется уравнение равновесия правой отсеченной части фермы, которое является аналитическим выражением левой ветви линии влияния.

При составлении уравнений статики  используются те же способы, что и для определения усилий от неподвижной нагрузки. Обычно требуется две последовательные установки силы F = 1 – слева и справа от сечения. Поскольку в ферме нагрузка прикладывается только в узлах, то в пределах рассеченной панели левую и правую ветвь линии влияния следует соединить прямой.

При построении линий влияния в шпренгельной ферме, схемы фермы (заданная, основная и шпренгель) должны быть вычерчены заново, без нагрузки. Должны быть приведены все сечения и расчеты, а на полученных линиях влияния должны быть проставлены числовые значения ординат под каждым узлом фермы.

Максимальное расчетное усилие определяется суммой усилий от постоянной нагрузки и максимального усилия от временной нагрузки. Минимальное расчетное усилие равно сумме усилия от постоянной нагрузки и минимального усилия от временной нагрузки. Максимальные и минимальные расчетные усилия должны быть определены для всех восьми стержней и сведены в таблицу.

 

 

Задача 5. Расчет  плоской фермы с построением линий влияния

Для плоской фермы (рис. 8, табл. 5) построить эпюру нормальных сил.

Таблица 5

Номер

cтроки

Номер схемы

по рис.8

F/P

01

I

1

02

II

2

03

III

3

04

IV

1

05

V

2

06

VI

–1

07

VII

–2

08

VIII

–3

09

IX

–1

10

X

–2

11

I

1

12

II

2

13

III

3

14

IV

1

15

V

2

16

VI

–1

17

VII

1

18

VIII

2

19

IX

3

20

X

1

21

I

2

22

II

–1

23

III

–2

24

IV

–3

25

V

–1

26

VI

–2

27

VII

1

28

VIII

2

29

IX

3

30

X

1

31

I

2

32

II

–1

33

III

–2

34

IV

–3

35

V

–1

36

VI

–2

 

в

г

 

03a  03a

03a

03b

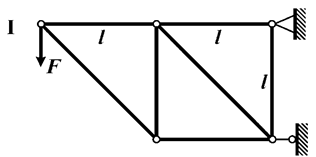
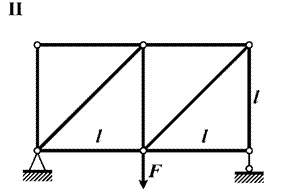
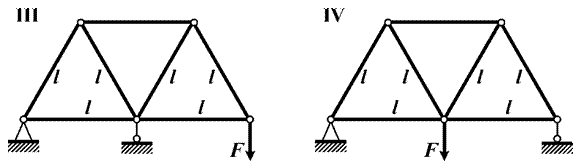
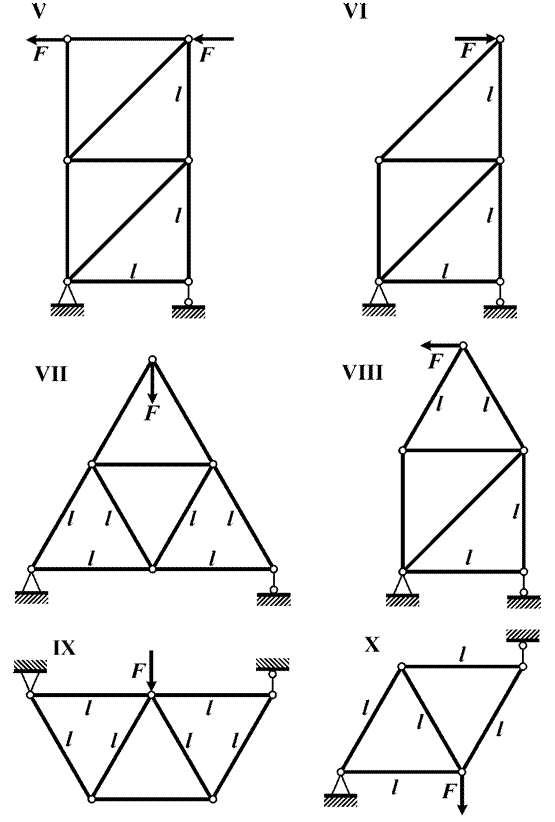
Рис. 8

 

 

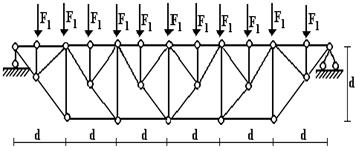
Задача 6. Расчет  плоской статически определимой балочной фермы на действие постоянной нагрузки

Для плоской балочной фермы (рис. 9) нагруженной постоянной  нагрузкой F приложенной в каждом узле ездового пояса фермы (показан пунктирной линией) кроме крайних узлов, где приложена нагрузка F/2, с выбранными по шифру из таблицы 6 размерами, требуется:

а) Произвести анализ геометрической неизменяемости фермы.

Необходимое и достаточное условие геометрической неизменяемости простейших по структуре образования ферм заключается в выполнении условия

С = 2У,                                                                         

где С – количество стержней фермы, включая опорные; У – количество узлов.

б) Определить усилия в стержнях заданной панели, включая левую и правую стойки, от действия нагрузки F.

 

Таблица 6

Номер

cтроки

Номер схемы

по рис.9

№ панели

фермы

(считая слева)

d,

м

h,

м

Постоянная

нагрузка

F, кН

01

1

4

6

8

200

02

2

5

8

10

180

03

3

6

4

6

160

04

4

7

6

9

140

05

5

8

9

12

120

06

6

9

6

6,6

100

07

7

8

8

8,8

80

08

8

7

4

6,6

60

09

9

6

5

7,5

220

10

10

5

6

7,2

240

11

1

4

6

8

200

12

2

5

6

10

180

13

3

6

8

6

160

14

4

7

4

9

140

15

5

8

6

12

120

16

6

9

9

6,6

100

17

7

8

6

8,8

80

18

8

7

8

6,6

60

19

9

6

4

7,5

220

20

10

5

5

7,2

240

21

1

4

6

8

200

22

2

5

6

10

180

23

3

6

6

6

160

24

4

7

8

9

140

25

5

8

4

12

120

26

6

9

6

6,6

100

27

7

8

9

8,8

80

28

8

7

6

6,6

60

29

9

6

8

7,5

220

30

10

5

4

7,2

240

31

1

4

5

8

200

32

2

5

6

10

180

33

3

6

6

6

160

34

4

7

6

9

140

35

5

8

8

12

120

36

6

9

4

6,6

100

 

а

г

а

б

в

 

1 схема

 

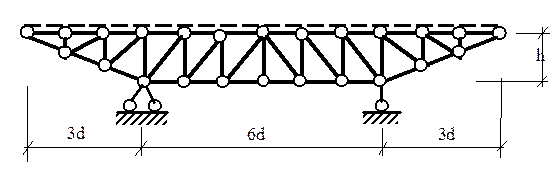
2 схема

 

3 схема

 

4 схема

 

5 схема

 

6 схема

 

7 схема

 

8 схема

 

9 схема

 

10 схема

Рис. 9

 

 

Задача 7. Расчет  плоской статически определимой балочной фермы на действие подвижной нагрузки

Для плоской балочной фермы (рис. 10) нагруженной постоянной  нагрузкой F приложенной в каждом узле ездового пояса фермы (показан пунктирной линией) кроме крайних узлов, где приложена нагрузка F/2, с выбранными по шифру из таблицы 9 размерами, требуется:

1) Построить линии влияния опорных реакций.

2) Построить линии влияния усилий для стержней заданной панели, включая левую и правую стойки, воспользовавшись способом сечений или способом вырезания узлов.

При использовании способа сечений достаточно составить уравнение одной из ветвей линии влияния, выразив его через линию влияния опорной реакции. Для построения второй ветви можно воспользоваться следующими положениями:

а) в балочной ферме нулевые точки ветвей линий влияния находятся под опорными узлами;

б)  левая и правая ветви линии влияния пересекаются под моментной точкой;

в) если моментная точка находится в бесконечности, левая и правая ветви линии влияния должны быть параллельны.

3) Определить по линиям влияния значения усилий от действия неподвижной нагрузки.

4) Определить по линиям влияния максимальные и минимальные значения усилия от подвижной нагрузки АК (таблица 7).

 

Таблица 7. Основные показатели нормативных подвижных нагрузок

Примечание: При действии нагрузки АК равномерно распределенная нагрузка не учитывается.

 

5. Определить расчетные величины усилий в стержнях заданной панели от неподвижной и подвижной нагрузок.  Результаты представить в табличной форме (табл. 8).

 

Таблица 8. Вычисление расчетных усилий

 

Стержень

Усилие от

неподвижной

нагрузки, кН

Усилие от подвижной

нагрузки, кН

Расчетное усилие,

кН

max.

min.

max.

min.

 

 

 

 

 

 

 

 

Таблица 9

Номер

cтроки

Номер схемы

по рис.10

№ панели

фермы

(считая слева)

d,

м

h,

м

Постоянная

нагрузка

F, кН

01

1

4

6

8

200

02

2

5

8

10

180

03

3

6

4

6

160

04

4

7

6

9

140

05

5

8

9

12

120

06

6

9

6

6,6

100

07

7

8

8

8,8

80

08

8

7

4

6,6

60

09

9

6

5

7,5

220

10

10

5

6

7,2

240

11

1

4

6

8

200

12

2

5

6

10

180

13

3

6

8

6

160

14

4

7

4

9

140

15

5

8

6

12

120

16

6

9

9

6,6

100

17

7

8

6

8,8

80

18

8

7

8

6,6

60

19

9

6

4

7,5

220

20

10

5

5

7,2

240

21

1

4

6

8

200

22

2

5

6

10

180

23

3

6

6

6

160

24

4

7

8

9

140

25

5

8

4

12

120

26

6

9

6

6,6

100

27

7

8

9

8,8

80

28

8

7

6

6,6

60

29

9

6

8

7,5

220

30

10

5

4

7,2

240

31

1

4

5

8

200

32

2

5

6

10

180

33

3

6

6

6

160

34

4

7

6

9

140

35

5

8

8

12

120

36

6

9

4

6,6

100

 

а

г

а

б

в

 

1 схема

 

2 схема

 

3 схема

 

4 схема

 

5 схема

 

6 схема

 

7 схема

 

8 схема

 

9 схема

 

10 схема

Рис. 10

 

 

Задача 8. Расчет  распорных и комбинированных систем

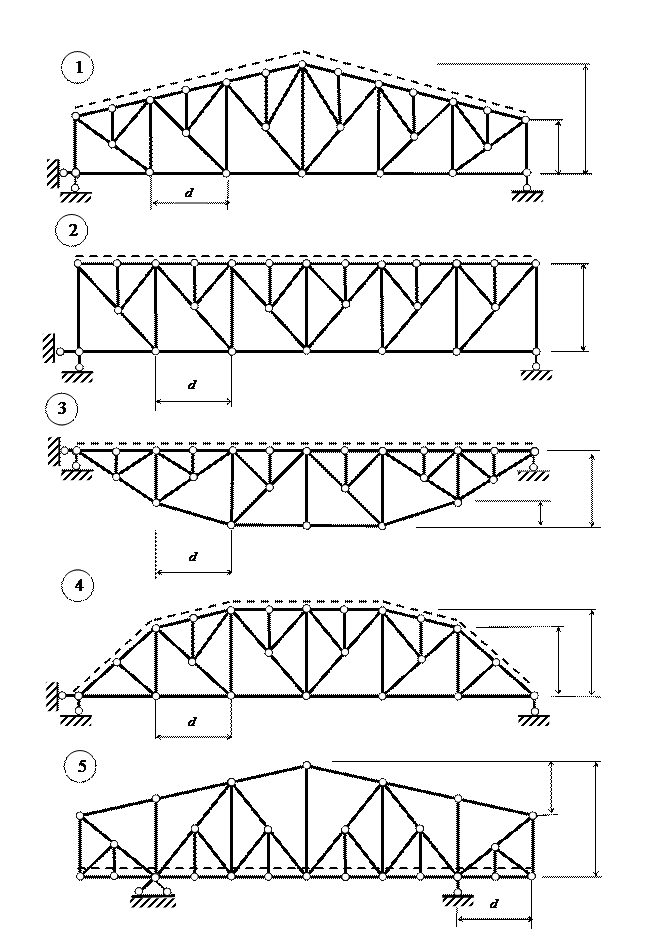
Для одной из стержневых систем, изображенных на рис. 11 требуется:

1) выполнить кинематический анализ;

2) определить внутренние силовые факторы в указанных сечениях.

Исходные данные для расчета принять из табл. 10.

Таблица 10

Номер

строки

Схемы балок

рис. 11

l, м

F, кН

01

1 

2

5

02

2

1

7

03

3

1,5

9

04

4

1,5

10

05

5

1

8

06

6

2

6

07

7

2,5

4

08

8

1

6

09

9

1,75

7

10

10

2

9

11

11

2,5

5

12

12

2

4

13

1 

1

6

14

2

1,75

5

15

3

2

10

16

4

2,5

8

17

5

1

5

18

6

1,5

5

19

7

2

8

20

8

3

9

21

9

2,5

9

22

10

2

10

23

11

1

5

24

12

3

6

25

1 

1

6

26

2

1,75

7

27

3

2

9

28

4

2,5

5

29

5

2

4

30

6

1

6

31

7

1,75

5

32

8

2

10

33

9

2,5

8

34

10

1

5

35

11

1,5

5

36

12

2

8

 

а

б

г

 

Схема 1                                          Схема 2

1

 

  

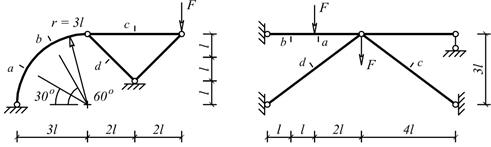
Схема 3                                          Схема 4

1

 

 

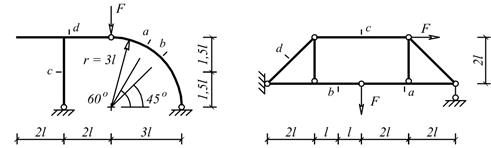
Схема 5                                          Схема 6

1

 

 

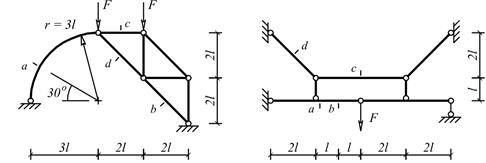
Схема 7                                          Схема 8

1

 

 

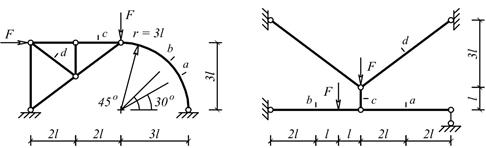
Схема 9                                          Схема 10

1

 

 

Схема 11                                          Схема 12

1

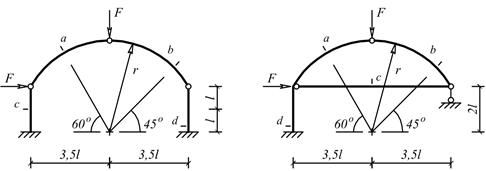
Рис. 11

 

Пример решения задачи

Этот раздел предусмотрен для студентов, желающих доказать, что они способны решать задачи статики стержневых систем повышенной сложности. Поэтому пример решения здесь не приводится.

 

Пояснения к решению задачи

1) В распорных системах при вертикальной нагрузке возникают реакции (распор) в горизонтальных связях (затяжках, распорках и др.). Найдите реакции в связях.

2) Сложности возникают не только при определении реакций в связях, но и при доказательстве, что рассматриваемая конструктивная схема является статически определимой, т.е. кинематически неизменяемой, у которой степень свободы равна нулю. Преодолейте эти трудности.

 

 

Задача 9. Расчет  плоской статически определимой шпренгельной фермы

Для плоской шпренгельной фермы (рис. 12) нагруженной постоянной  нагрузкой F в узлах пояса, отмеченного пунктиром,  с выбранными по шифру из таблицы 11 размерами, требуется:

а) определить (аналитически) усилия в стержнях заданной панели, включая правую стойку (4 стержня);

б) построить линии влияния усилий в тех же стержнях;

в) установить наиболее опасное положение временной нагрузки для каждого стержня заданной панели отдельно и найти величины максимальных и минимальных усилий;

г) определить максимальные и минимальные значения расчетных усилий во всех стержнях заданной панели (с учетом постоянной нагрузки).

 

Таблица 11

Номер

cтроки

Номер схемы

по рис.12

№ панели

фермы

(считая слева)

d,

м

h,

м

Постоянная

нагрузка

F, кН

Временная

нагрузка

Fвр, кН

01

1

2

3,0

3,2

12,0

16,0

02

2

3

3,5

4,0

12,5

17,0

03

3

4

4,0

3,8

13,0

18,0

04

4

5

4,5

3,3

13,5

18,5

05

5

2

3,6

3,6

11,5

17,5

06

6

3

4,2

3,0

11,0

19,0

07

7

4

2,7

4,2

20,0

20,0

08

8

5

3,2

4,1

19,0

22,5

09

9

2

3,3

3,7

18,0

24,0

10

0

3

3,4

3,5

17,5

23,0

11

1

2

3,0

3,2

12,0

16,0

12

2

3

3,5

4,0

12,5

17,0

13

3

4

4,0

3,8

13,0

18,0

14

4

5

4,5

3,3

13,5

18,5

15

5

2

3,6

3,6

11,5

17,5

16

6

3

4,2

3,0

11,0

19,0

17

7

4

2,7

4,2

20,0

20,0

18

8

5

3,2

4,1

19,0

22,5

19

9

2

3,3

3,7

18,0

24,0

20

0

3

3,4

3,5

17,5

23,0

21

1

2

3,0

3,2

12,0

16,0

22

2

3

3,5

4,0

12,5

17,0

23

3

4

4,0

3,8

13,0

18,0

24

4

5

4,5

3,3

13,5

18,5

25

5

2

3,6

3,6

11,5

17,5

26

6

3

4,2

3,0

11,0

19,0

27

7

4

2,7

4,2

20,0

20,0

28

8

5

3,2

4,1

19,0

22,5

29

9

2

3,3

3,7

18,0

24,0

30

0

3

3,4

3,5

17,5

23,0

31

1

2

3,0

3,2

12,0

16,0

32

2

3

3,5

4,0

12,5

17,0

33

3

4

4,0

3,8

13,0

18,0

34

4

5

4,5

3,3

13,5

18,5

35

5

2

3,6

3,6

11,5

17,5

36

6

3

4,2

3,0

11,0

19,0

 

в

г

а

б

в

б

 

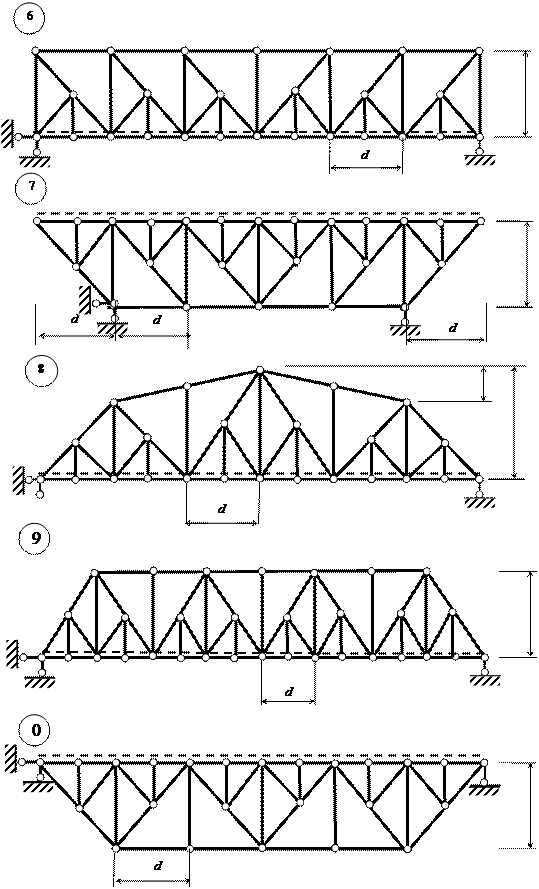
Подпись: hПодпись: hПодпись: 1,2hПодпись: h/3Подпись: h Подпись: h/2Подпись: h h h hПодпись: h/2Подпись: h

 

Подпись: hПодпись: hПодпись: h/2Подпись: hПодпись: hПодпись: h

Рис.12

 

Пояснения к решению задачи

По условию задачи требуется определить усилия не во всех стержнях фермы, а только в стержнях заданной панели. В этом случае удобно воспользоваться способом сквозных сечений.

Сущность способа состоит в следующем: ферму рассекают на две части таким образом, чтобы в разрез попало не более трех стержней  с неизвестными усилиями; одну из частей мысленно отбрасывают, а ее действие на оставшуюся заменяют усилиями. Затем составляют уравнения моментов относительно моментных точек, (находящихся на пересечении двух из трех стержней), или уравнения проекций, если два из пересекаемых стержней параллельны. Таким образом, можно получить три уравнения и в каждом будет по одному неизвестному.

Особенность расчета шпренгельных ферм является то, что для некоторых стержней нельзя провести удачного сечения (пересекающего не более трех стержней). В связи с этим появляется необходимость переходить к схеме взаимодействия шпренгеля с основной решеткой. Для этого необходимо предварительно выделить основную и дополнительную решетки и установить схемы их взаимодействия с основной решеткой, т.е. схемы передачи нагрузки со шпренгелей в узлы основной фермы.

Для успешного расчленения заданной фермы на основную и шпренгель необходимо твердо усвоить типы шпренгелей.

Следует иметь в виду, что в большинстве случаев (для всех заданных ферм) усилия в элементах, входящих и в шпренгель и в основную решетку удается определить, рассматривая непосредственно заданную ферму. В связи с этим рекомендуется сначала рассмотреть заданную схему и найти  все усилия, для которых возможно провести удачное сечение.

Остальные усилия определяются из рассмотрения только шпренгеля или только основной решетки. При этом в работе обязательно нужно приводить схемы шпренгеля и основной решетки отдельно с указанием узловой нагрузки, полученной в результате передачи местной нагрузки со шпренгеля в узлы основной решетки.

Производя определение усилий, надо приводить все схемы, разрезы и указывать все величины, входящие в расчетные формулы. Геометрические характеристики (плечи, углы и пр.) должны быть определены аналитически, а не графически.

Построение линий влияния усилий в стержнях ферм начинают с построения линий влияния опорных реакций. Для балочных ферм, эти линии влияния имеет такой же вид, как и  линии влияния опорных реакций балок того же пролета. Затем груз F = 1 устанавливается в произвольном узле фермы по одну сторону от сечения (например, слева). Для определения усилия составляется уравнение равновесия правой отсеченной части фермы, которое является аналитическим выражением левой ветви линии влияния.

При составлении уравнений статики  используются те же способы, что и для определения усилий от неподвижной нагрузки. Обычно требуется две последовательные установки силы F = 1 – слева и справа от сечения. Поскольку в ферме нагрузка прикладывается только в узлах, то в пределах рассеченной панели левую и правую ветвь линии влияния следует соединить прямой.

При построении линий влияния в шпренгельной ферме, схемы фермы (заданная, основная и шпренгель) должны быть вычерчены заново, без нагрузки. Должны быть приведены все сечения и расчеты, а на полученных линиях влияния должны быть проставлены числовые значения ординат под каждым узлом фермы.

Максимальное расчетное усилие определяется суммой усилий от постоянной нагрузки и максимального усилия от временной нагрузки. Минимальное расчетное усилие равно сумме усилия от постоянной нагрузки и минимального усилия от временной нагрузки. Максимальные и минимальные расчетные усилия должны быть определены для всех восьми стержней и сведены в таблицу.

 

 

Задача 10. Расчет  плоской статически определимой фермы при постоянной и подвижной нагрузке

Для заданной фермы (рис.14), загруженной равномерно распределенной постоянной нагрузкой и испытывающей воздействие подвижной системы грузов, требуется:

1) Определить аналитически усилия от воздействия постоянной нагрузки в указанной панели фермы для следующих стержней:

- 1 элемент нижнего пояса;

- 1 элемент верхнего пояса;

- 1 стойка;

- 2 раскоса;

2) Построить линии влияния в указанных стержнях.

3) Установить наиболее опасное положение подвижной нагрузки для получения максимального и минимального значения усилия для любых (кроме 2-й категории) двух из заданных стержней фермы.

4) Определить максимальные и минимальные расчетные усилия в этих стержнях фермы (с учетом постоянной и временной нагрузок).

5) Определить с помощью ЭВМ усилия во всех стержнях фермы от воздействия постоянной нагрузки.

Размеры, нагрузки, схема подвижной конструкции даны на рис.13 и 14 и в таблице 12.

Таблица 12

Номер

cтроки

Номер схемы

по рис.14

№ панели

фермы

(считая слева)

Длина панели

d, м

Расстояние

между

фермами

с, м

Постоянная

нагрузка

q, кН/м2

Временная

Нагрузка (рис.13)

P1,

кН

P2,

кН

P3,

кН

P4,

кН

a,

м

b,

м

01

10

2

1,5

3

250

15

20

10

10

0,2

2,0

02

9

3

2,0

4

225

10

15

8

10

0,2

1,8

03

8

4

2,5

5

200

8

7

15

10

0,3

1,6

04

7

5

3,0

6

175

10

15

15

7

0,4

1,4

05

6

2

3,5

7

180

5

7

7

10

0,5

1,2

06

5

3

4,0

8

160

12

6

7

10

0,6

1,0

07

4

4

2,0

9

150

6

10

10

8

0,7

0,8

08

3

5

2,5

4

280

10

8

10

8

0,8

0,6

09

2

2

3,5

5

300

15

10

20

10

0,9

0,4

10

1

3

4,0

6

225

8

10

20

10

1

0,2

11

10

2

1,5

3

250

15

20

10

10

0,2

2,0

12

9

3

2,0

4

225

10

15

8

10

0,2

1,8

13

8

4

2,5

5

200

8

7

15

10

0,3

1,6

14

7

5

3,0

6

175

10

15

15

7

0,4

1,4

15

6

2

3,5

7

180

5

7

7

10

0,5

1,2

16

5

3

4,0

8

160

12

6

7

10

0,6

1,0

17

4

4

2,0

9

150

6

10

10

8

0,7

0,8

18

3

5

2,5

4

280

10

8

10

8

0,8

0,6

19

2

2

3,5

5

300

15

10

20

10

0,9

0,4

20

1

3

4,0

6

225

8

10

20

10

1

0,2

21

10

2

1,5

3

250

15

20

10

10

0,2

2,0

22

9

3

2,0

4

225

10

15

8

10

0,2

1,8

23

8

4

2,5

5

200

8

7

15

10

0,3

1,6

24

7

5

3,0

6

175

10

15

15

7

0,4

1,4

25

6

2

3,5

7

180

5

7

7

10

0,5

1,2

26

5

3

4,0

8

160

12

6

7

10

0,6

1,0

27

4

4

2,0

9

150

6

10

10

8

0,7

0,8

28

3

5

2,5

4

280

10

8

10

8

0,8

0,6

29

2

2

3,5

5

300

15

10

20

10

0,9

0,4

30

1

3

4,0

6

225

8

10

20

10

1

0,2

31

10

2

1,5

3

250

15

20

10

10

0,2

2,0

32

9

3

2,0

4

225

10

15

8

10

0,2

1,8

33

8

4

2,5

5

200

8

7

15

10

0,3

1,6

34

7

5

3,0

6

175

10

15

15

7

0,4

1,4

35

6

2

3,5

7

180

5

7

7

10

0,5

1,2

36

5

3

4,0

8

160

12

6

7

10

0,6

1,0

 

а

б

в

г

в

б

а

г

б

в

а

 

Рис. 13

 

 

Рис. 14

 

 

Примеры выполнения задач

 

Пример 1. Пример расчета фермы на неподвижную нагрузку

Проведем расчет фермы, изображенной на рис. 15.

 

1) Определение опорных реакций от заданной нагрузки

 

Рис. 15. Заданная ферма

 

Определим линейную нагрузку, при

При действии на ферму вертикальной нагрузки  возникают две опорные реакции  и , определяемые из следующих уравнений статики.

1. Равенство нулю суммы моментов всех сил относительно шарнира B, из которого определяется опорная реакция .

2. Равенство нулю суммы моментов всех сил относительно шарнира A, из которого определяется опорная реакция .

Проверка правильности вычисления опорных реакций осуществляется по формуле

Реакции вычислены верно.

 

2) Определение продольных усилий в стержнях шпренгельной решетки

 

Для  определения продольных усилий перераспределим внешнюю нагрузку  в узлы шпренгельной фермы:

где  – силы в крайних узлах фермы;

 – силы во всех остальных узлах фермы.

Снимаем шпренгельную фермочку и известными способами определим усилия в стержнях (рис. 16).

Рис.16. Расчетная схема шпренгеля.

 

Проверку осуществим по формуле

Реакции вычислены верно.

Усилия в стержнях 1-го узла определим методом вырезания узлов (рис. 17).

Рис.17. Расчетная схема для определения усилий S12 и S14

 

Узел 1.

Поскольку шпренгельная фермочка симметрична, то

Вырезаем узел 2 и определяем усилия в стержне 2-4 (рис. 18).

Рис.18. Расчетная схема для определения усилий S24

 

Узел 2.

 

 

3) Определение усилий в стержнях основной фермы

Перераспределим внешнюю нагрузку в узлы основной фермы. Определим узловую нагрузку основной фермы  и   (рис. 19).

Рис.19. Расчетная схема основной фермы

 

Опорные реакции основной фермы равны опорным реакциям шпренгельной фермы.

Определим усилия  в стержне 1-3 методом моментных точек. Для этого разрежем панель сечением I-I. При определении усилия  моментной точкой является узел 6.

Так как усилие  имеет отрицательный знак, то стержень 1-3 сжат.

Усилие  определяем методом проекций:

Усилие  отрицательно, следовательно, стержень 1-6 сжат.

Усилие  определяем методом моментных точек. Моментной точкой является узел 1.

Усилие  в стержне 3-6 определим методом вырезания узлов (рис. 20).

Рис.20. Расчетная схема для определения усилия S4

 

Узел 3.               

Усилие  в стержне 1-5 определяем методом проекций, после рассечения фермы сечением II-II (рис. 21).

 

Рис.21. Расчетная схема для определения усилия S5 в стержне 1-5

 

 

4) Определение усилий в стержнях шпренгельной фермы

У данной на рис. 15 фермы имеются стержни трех категорий:

1 – все стержни верхнего пояса, все длинные стойки  и все стержни типа 4-6;

2 – принадлежащие  только шпренгелю – все короткие стойки и раскосы типа 3-4;

3 – принадлежащие и основной ферме и шпренгельной фермочке, стержни типа 1-4, 1-2, 2-3.

Продольные усилия в стержнях шпренгельной фермы обозначим через N.

 

 

 

 

 

 

 

 

5) Построение линий влияния в стержнях шпренгельных ферм

Линии влияния опорных реакций

Приведем формулы вертикальных опорных реакций, которые будут необходимы для вывода аналитических выражений усилий в стержнях фермы и построения их линий влияния. При принятой системе координат с началом на опоре B аналитическое выражение   и   найдем соответственно из выражений

откуда при 

Вычисляем численные значения  и

Линии влияния опорных реакций показаны на рис. 22, а, б.

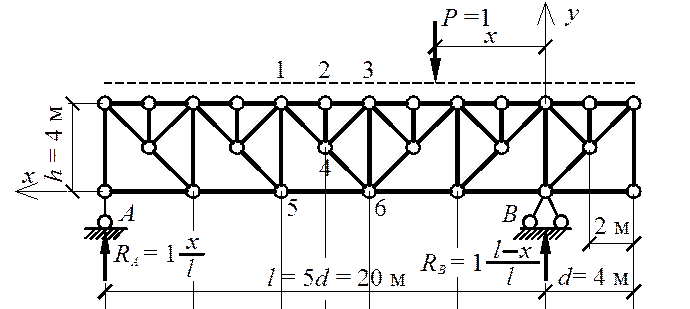
Рис.22. Линии влияния опорных реакций

 

 

6) Построение линий влияния продольных сил в стержнях указанной панели

Линии влияния  усилий в стержнях шпренгельной фермочки

 

1. Примем  в узлах 1 или 3. Стержни шпренгеля не работают, поэтому

2. Примем  в узле 2, в этом случае методом вырезания узлов определяем усилия во всех стержнях шпренгеля (рис. 23).

Рис.23. Расчетная схема для определения усилия S12 и S14 от P = 1 в узле 1

 

Поскольку шпренгель симметричный, то

Вырезаем узел 2 (рис. 24).

Рис.24. Расчетная схема для определения усилия S24  от P = 1 в узле 2

 

По найденным значениям ординат строятся л. в. , л. в. , л. в. , рис. 25

.

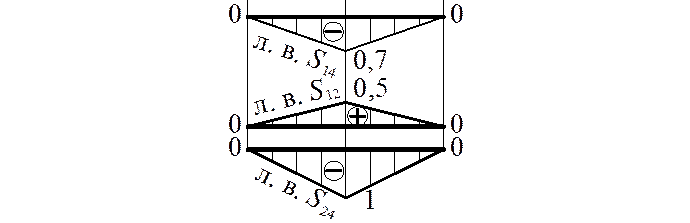
Рис.25

 

 

7) Линии влияния усилий в стержнях основной фермы

 

Для построения линий влияния разрежем панель сечением I-I (рис. 26).

Построение л. в.  в стержне 1-3.

Рис.26. Схема для построения л. в. усилий S1, S2, S3, S4 в стержнях основной фермы

 

Рассмотрим равновесие правой отсеченной части

Характерные ординаты продольной силы равны:

 

 

Рассмотрим равновесие левой отсеченной части.

 

 

 

Линия влияния  показана на рис. 3.20.

Построение л. в.  в стержне 1-6.

 

 

 

 

 

Линия влияния показана на рис. 3.20.

Построение л. в.  в стержне 5-6.

 

 

 

 

 

Линия влияния    показана на рис. 3.20.

Построение л. в. в стержне 3-6.

Усилие  от действия единичной силы определяем, вырезав узел 2 (рис. 27).

Рис.27. Определение усилия S4 от P = 1 в узле 2

 

Построение л. в.  в стержне 1-5 основной фермы.

Рассекаем основную ферму сечением II-II на две части, так чтобы сечение проходило через три стержня (рис. 28).

Рис.28. Схема к построению л. в. S5 в стержне 1-5

 

Рассмотрим равновесие правой части.

 

 

Рассмотрим равновесие левой части.

 

 

 

По вычисленным значениям ординат строим линию влияния усилия  (рис. 3.22).

 

8) Построение линий влияния усилий в стержнях шпренгельной фермы

Линии влияния продольных усилий в стержнях шпренгельной фермы построены методом наложения.

В стержнях 1-й категории шпренгельной фермы л. в. совпадают с л. в. соответствующих стержней основной фермы (рис. 29, а, б, в, г).

В стрежнях 2-й категории шпренгельной фермы л. в. совпадают с л. в. соответствующих стержней шпренгельной решетки (рис. 29, д, е).

В стержнях 3-й категории шпренгельной фермы л. в. получают алгебраическим суммированием соответственно л. в. стержней 1-й и 2-й категории (рис. 29, ж, з).

ЛВ N56= ЛВ S3 (стержень 1-й категории).

ЛВ N64= ЛВ S2 (стержень 1-й категории).

ЛВ N26= ЛВ S4 (стержень 1-й категории).

ЛВ N15= ЛВ S5 (стержень 1-й категории).

ЛВ N24= ЛВ S24 (стержень 2-й категории).

ЛВ N34= ЛВ  S34 (стержень 2-й категории).

ЛВ N13= ЛВ S2+ЛВ S14 (стержень 3-й категории).

ЛВ N12= ЛВ N23=ЛВ S1+ЛВ S12 (стержень 3-й категории).

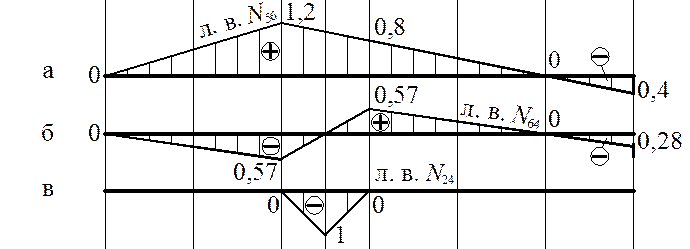
Рис.29. Линии влияния продольных усилий в стержнях

1 категории а, б, в, г; 2 категории д, е; 3 категории ж, з

 

 

9) Определение max N и min N в стержнях шпренгельной фермы от совместного действия постоянной и временной нагрузки

 

Величины максимальных и минимальных продольных усилий от совместного действия постоянной и временной нагрузки определяются следующим образом:

где  продольная сила в стержне от действия постоянной  и положительной временной нагрузки ;

 продольная сила в стержне от действия постоянной   и отрицательной временной нагрузки .

Усилие   по линии влияния от заданной нагрузки  определится по формуле

где ω  площадь участка линии влияния усилия  под нагрузкой .

Усилие , определенное другим способом, стр. 12:

 

10) Определение  от временной нагрузки в стержне 5-6.

 

Используется ранее построенная линия влияния продольной силы   (рис. 29, а) и вновь показанная на рис. 30.

Рис.30. Схема к определению опасного положения

временной нагрузки для стержня 5-6

 

Для определения критической силы и по ней опасное положение временной нагрузки, нужно проверить выполнение условия

Найдем тангенсы угла наклона линии влияния под нагрузкой по рис. 30.

1. Пусть сила  является критической.

а) Примем  левее положительной вершины K линии влияния .

б) Примем  правее этой же вершины K линии влияния .

Сила  не является критической, так как не меняет знак функции

2. Пусть сила  является критической.

а)  Примем  левее вершины K линии влияния .

б) Примем  правее вершины K линии влияния .

Сила  не является критической, так как не меняет знак функции

3. Пусть сила  является критической.

а)  Примем  левее вершины K линии влияния .

б) Примем  правее вершины K линии влияния .

Сила  является критической, поскольку поменялся знак функции  при переходе через вершину K л. в.  на противоположный.

4. Пусть сила  является критической.

а)  Примем  левее вершины K линии влияния .

б) Примем  правее вершины K линии влияния .

Сила  не является критической, так как не меняет знак функции

Нагрузка займет опасное положение для стержня 5-6, когда сила  находится в первом узле шпренгельной фермы. В этом случае возникает наибольшая положительная сила в стержне 5-6 от временной нагрузки. Найдем это усилие:

где  - ординаты линии влияния усилия  под соответствующими нагрузками (рис. 29), 

Ординаты  определяем из пропорций:

Определяем  от совместного действия постоянной и временной нагрузки:

Стержень растянут от совместного действия этих нагрузок.

 

11) Определение  от временной нагрузки в стержне 5-6

 

В этом случае лучше определять продольные силы от действия всех четырех сил, когда они находятся под отрицательной вершиной линии влияния :

 над вершиной K1

P2 над вершиной K1

P3 над вершиной K1

P4 над вершиной K1

Временная нагрузка займет опасное положение, когда третий груз находится над вершиной K1 линии влияния . В этом случае в стержне 5-6 будет максимально отрицательная продольная сила, равная –23 кН.

Определим минимальную продольную силу в стержне 5-6 от совместного действия постоянной и временной нагрузки:

Поперечное сечение стержня определяется в зависимости от действия продольной силы

По этой методике определяются расчетные усилия и для других стержней. При наличии нескольких положительных и отрицательных вершин на линии влияния стержня для всех случаев определяют опасные положения, по ним вычисляются  продольные силы от временной нагрузки, а за расчетные берутся наибольшие значения.

 

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

 

Теоретическая механика   Сопротивление материалов

Прикладная механика  Детали машин  Теория машин и механизмов

 

 

 

 

00:00:00

 

Top.Mail.Ru