Главная
Задача 1. Расчет статически неопределимых
ферм
Для заданной статически неопределимой фермы (рис.1) с
заданными в табл.1 нагрузками требуется определить опорные реакции.
Таблица 1
|
Номер cтроки |
Схема по рис.1 |
P, кН |
Q, кН |
|
01 |
1 |
10 |
7 |
|
02 |
2 |
8 |
6 |
|
03 |
3 |
5 |
3 |
|
04 |
4 |
6 |
4 |
|
05 |
5 |
9 |
7 |
|
06 |
6 |
10 |
8 |
|
07 |
7 |
11 |
6 |
|
08 |
8 |
12 |
7 |
|
09 |
9 |
6 |
7 |
|
10 |
10 |
5 |
5 |
|
11 |
11 |
11 |
4 |
|
12 |
12 |
7 |
3 |
|
13 |
13 |
5 |
4 |
|
14 |
14 |
6 |
9 |
|
15 |
15 |
12 |
8 |
|
16 |
16 |
13 |
7 |
|
17 |
17 |
10 |
4 |
|
18 |
18 |
10 |
5 |
|
19 |
19 |
6 |
6 |
|
20 |
20 |
10 |
3 |
|
21 |
21 |
7 |
7 |
|
22 |
22 |
11 |
8 |
|
23 |
23 |
9 |
5 |
|
24 |
24 |
7 |
4 |
|
25 |
25 |
6 |
9 |
|
26 |
26 |
8 |
7 |
|
27 |
27 |
8 |
4 |
|
28 |
28 |
10 |
9 |
|
29 |
29 |
9 |
3 |
|
30 |
30 |
12 |
9 |
|
31 |
31 |
8 |
7 |
|
32 |
32 |
7 |
8 |
|
33 |
33 |
6 |
3 |
|
34 |
34 |
8 |
9 |
|
35 |
35 |
7 |
5 |
|
36 |
36 |
8 |
4 |
|
|
а |
г |
в |
1 схема
2 схема
3 схема
4 схема
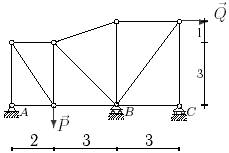
5 схема
6 схема
7 схема
8 схема
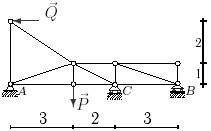
9 схема
10 схема
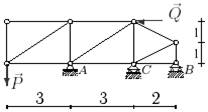
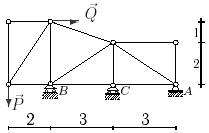
11 схема
12 схема
13 схема
14 схема
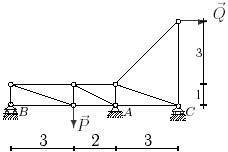
15 схема
16 схема
17 схема
18 схема
19 схема
20 схема
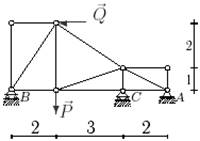
21 схема
22 схема
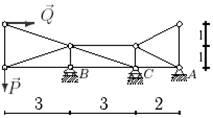
23 схема
24 схема
25 схема 26 схема
27 схема
28 схема
29 схема
30 схема
31 схема
32 схема
33 схема
34 схема
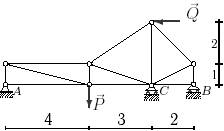
35 схема
36 схема
Рис.1
Задача 1. Расчет статически неопределимых
ферм
Для заданной статически неопределимой фермы (рис.2) с
заданными в табл.2 размерами и нагрузками требуется определить усилия во всех стержнях.
Таблица 2
|
Номер cтроки |
Схема по рис.2 |
d, м |
h, м |
P, кН |
Площади сечений |
|||
|
Нижнего пояса |
Верхнего пояса |
Решетки |
Элементов шпренгеля |
|||||
|
01 |
1 |
3,0 |
3,2 |
2 |
F |
1,5 F |
1,2 F |
F |
|
02 |
2 |
3,2 |
3,0 |
3 |
1,2 F |
1,7 F |
F |
1,5 F |
|
03 |
3 |
3,5 |
3,1 |
4 |
1,4F |
2 F |
2 F |
0,8 F |
|
04 |
4 |
2,9 |
2,9 |
5 |
1,6 F |
1,6 F |
0,8 F |
1,1 F |
|
05 |
5 |
3,3 |
3,3 |
6 |
1,8 F |
1,4 F |
0,9 F |
0,9 F |
|
06 |
6 |
3,4 |
3,4 |
7 |
1,3 F |
1,3 F |
1,3 F |
1,2 F |
|
07 |
7 |
3,6 |
3,5 |
8 |
1,5 F |
F |
1,1 F |
1,3 F |
|
08 |
8 |
3,1 |
3,6 |
9 |
1,7 F |
1,1 F |
1,5 F |
1,4 F |
|
09 |
9 |
3,7 |
3,7 |
10 |
1,1 F |
1,2 F |
0,7 F |
1,6 F |
|
10 |
10 |
3,8 |
3,8 |
12 |
2 F |
1,8 F |
1,4 F |
0,7 F |
|
11 |
11 |
3,0 |
3,2 |
2 |
F |
1,5 F |
1,2 F |
F |
|
12 |
12 |
3,2 |
3,0 |
3 |
1,2 F |
1,7 F |
F |
1,5 F |
|
13 |
13 |
3,5 |
3,1 |
4 |
1,4F |
2 F |
2 F |
0,8 F |
|
14 |
14 |
2,9 |
2,9 |
5 |
1,6 F |
1,6 F |
0,8 F |
1,1 F |
|
15 |
15 |
3,3 |
3,3 |
6 |
1,8 F |
1,4 F |
0,9 F |
0,9 F |
|
16 |
16 |
3,4 |
3,4 |
7 |
1,3 F |
1,3 F |
1,3 F |
1,2 F |
|
17 |
17 |
3,6 |
3,5 |
8 |
1,5 F |
F |
1,1 F |
1,3 F |
|
18 |
18 |
3,1 |
3,6 |
9 |
1,7 F |
1,1 F |
1,5 F |
1,4 F |
|
19 |
19 |
3,7 |
3,7 |
10 |
1,1 F |
1,2 F |
0,7 F |
1,6 F |
|
20 |
20 |
3,8 |
3,8 |
12 |
2 F |
1,8 F |
1,4 F |
0,7 F |
|
21 |
21 |
3,0 |
3,2 |
2 |
F |
1,5 F |
1,2 F |
F |
|
22 |
22 |
3,2 |
3,0 |
3 |
1,2 F |
1,7 F |
F |
1,5 F |
|
23 |
23 |
3,5 |
3,1 |
4 |
1,4F |
2 F |
2 F |
0,8 F |
|
24 |
24 |
2,9 |
2,9 |
5 |
1,6 F |
1,6 F |
0,8 F |
1,1 F |
|
25 |
25 |
3,3 |
3,3 |
6 |
1,8 F |
1,4 F |
0,9 F |
0,9 F |
|
26 |
1 |
3,4 |
3,4 |
7 |
1,3 F |
1,3 F |
1,3 F |
1,2 F |
|
27 |
2 |
3,6 |
3,5 |
8 |
1,5 F |
F |
1,1 F |
1,3 F |
|
28 |
3 |
3,1 |
3,6 |
9 |
1,7 F |
1,1 F |
1,5 F |
1,4 F |
|
29 |
4 |
3,7 |
3,7 |
10 |
1,1 F |
1,2 F |
0,7 F |
1,6 F |
|
30 |
5 |
3,8 |
3,8 |
12 |
2 F |
1,8 F |
1,4 F |
0,7 F |
|
31 |
6 |
3,0 |
3,2 |
2 |
F |
1,5 F |
1,2 F |
F |
|
32 |
7 |
3,2 |
3,0 |
3 |
1,2 F |
1,7 F |
F |
1,5 F |
|
33 |
8 |
3,5 |
3,1 |
4 |
1,4F |
2 F |
2 F |
0,8 F |
|
34 |
9 |
2,9 |
2,9 |
5 |
1,6 F |
1,6 F |
0,8 F |
1,1 F |
|
35 |
10 |
3,3 |
3,3 |
6 |
1,8 F |
1,4 F |
0,9 F |
0,9 F |
|
36 |
11 |
3,4 |
3,4 |
7 |
1,3 F |
1,3 F |
1,3 F |
1,2 F |
|
|
а |
г |
в |
б |
в |
а |
г |
б |
Рис.2
Пояснения к решению задачи
Усилия, площади поперечных сечений и модули упругости
по длине каждого стержня не меняются, поэтому интегрирование формулы Мора
сводится к суммированию:
Здесь за величину F0 удобно
принять F.
В первую очередь надо определить усилия во всех
стержнях основной системы от действия единичного неизвестного и нагрузки.
Расчет удобно свести в таблицу 3:
Таблица 3
|
№ стержня |
l, м |
|
|
|
|
|
|
|
|
Проверка
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Сумма величин, подсчитанных в столбце 7, дает значение
коэффициента канонического уравнения 
, а в столбце 8 – значение свободного члена 
.
При кинематической проверке (столбец 11) ошибка
допускается не более 2%.
Примеры
расчета статически неопределимых ферм
В статически неопределимой ферме помимо
связей, необходимых для геометрической неизменяемости, имеются лишние связи,
число которых характеризует степень статической неопределимости фермы. При расчёте
фермы методом сил следует иметь в виду, что при узловом приложении нагрузки в
стержнях фермы возникают лишь продольные силы N. Так как усилия, площади поперечных сечений и модули
упругости по длине стержня не меняются, то интегрирование по формуле Мора
сводится к суммированию.
Если ферма один раз статически
неопределима, то каноническое уравнение метода сил имеет вид:
Перемещения 
и 
определяют по
формулам:
где 
- продольные усилия в стержнях основной системы от
силы x1 = 1;
- продольные усилия в стержнях основной системы от внешней
нагрузки.
Окончательные усилия в любом стержне
фермы находят по формуле
Проверка расчёта статически
неопределимой фермы производится так же, как и в рамах. При статической
проверке необходимо убедиться в том, что узлы фермы находятся в равновесии. Для
статического контроля вычислений можно также воспользоваться формулой А.А.Уманского:
где Px и Py – проекции
действующих сил на оси X и Y;
x, y – координаты приложения нагрузок.
При этом начало координат можно выбрать
в любом месте; учитываются все внешние силы, в том числе и опорные реакции.
Кинематическая проверка должна
показать, что перемещение по направлению лишнего неизвестного равно нулю:
Допустимой можно считать невязку до 2%.
Пример
1.
Для статически неопределимой фермы с
заданными размерами и нагрузкой требуется определить усилия во всех стержнях (рис.
3).
Площади поперечных сечений стержней:
нижнего пояса F; верхнего пояса 1,5F; решетки 1,2F.
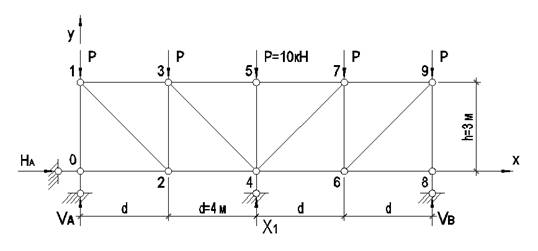
Рис.3
Решение.
Степень статической неопределимости
фермы найдем по формуле:
где С – число стержней фермы;
С0 – число опорных стержней;
У – число узлов фермы.
n = 17+4-2∙10 = 1.
Ферма один раз статически неопределима.
Основную систему получим путем отбрасывания среднего опорного стержня, реакцию
которого принимаем за лишнее неизвестное Х1.
Каноническое уравнение метода сил:
Загружаем основную систему по
отдельности силой Х1=1
и внешней нагрузкой. Находим, соответственно, продольные усилия в стержнях и Nр (рис. 4).
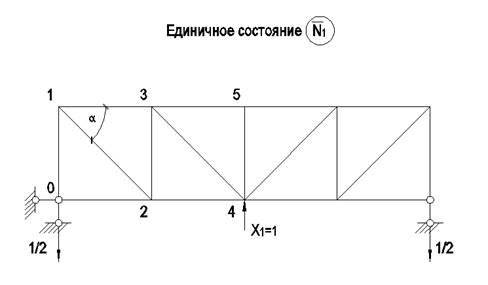
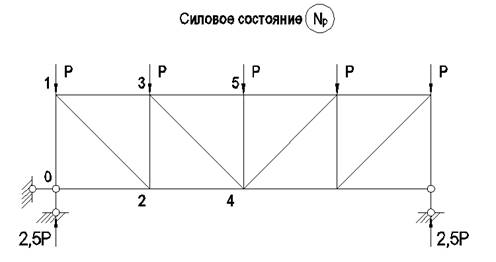
Рис.4
Весь расчет выполнен в таблице 4.
Вследствие симметрии в таблицу внесены данные, относящиеся к левой половине
фермы.
За величину F0 удобно
принять F, т.е. F0=F.
Таблица 4
|
№ стержня |
l, м |
|
|
|
кН |
|
|
|
Проверка
|
|
0-1 |
3,0 |
1/1,2 |
0,5 |
0,625 |
-25,0 |
-31,25 |
11,875 |
-13,125 |
-16,406 |
|
1-3 |
4,0 |
1/1,5 |
0,67 |
1,197 |
-20,0 |
-35,73 |
15,91 |
-4,09 |
-7,307 |
|
0-2 |
4,0 |
1,0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2-3 |
3,0 |
1/1,2 |
0,5 |
0,625 |
-15,0 |
-18,75 |
11,875 |
-3,125 |
-3,906 |
|
3-5 |
4,0 |
1/1,5 |
1,33 |
4,717 |
-26,67 |
-94,59 |
31,588 |
4,918 |
17,442 |
|
2-4 |
4,0 |
1 |
-0,67 |
1,796 |
20,0 |
-53,6 |
-15,91 |
4,09 |
-10,961 |
|
1-2 |
5,0 |
1/1,2 |
-0,83 |
2,87 |
25,0 |
-86,458 |
-19,712 |
5,288 |
-18,288 |
|
3-4 |
5,0 |
1/1,2 |
-0,83 |
2,87 |
8,33 |
-28,808 |
-19,712 |
-11,382 |
39,362 |
|
4-5 |
3,0 |
1/1,2 |
0 |
0 |
-10,0 |
0 |
0 |
-10,0 |
0 |
|
|
|
|
|
Σ=14,70 |
|
Σ=349,186 |
|
|
Σ=0,064 |
Таким образом, по таблице, имеем:
Статическую проверку расчёта выполним по
формуле А.Уманского:
ΣNili = -13,125∙3-4,09∙4-3,125∙3+4,918∙4+4,09∙4+5,288∙5-11,382∙5-10∙3=45,812-135,66=-89,848
Начало координат осей XY выбираем
на левой опоре.
Абсолютная ошибка равна (-0,152).
Погрешность составляет в процентах:
Кинематическая проверка (см. нижнюю
строку табл.4):
Погрешность составляет всего
Обе проверки показали, что расчёт выполнен верно.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Теория машин и механизмов
