Главная

Задача 1. Расчет перемещений в статически определимых двухопорных рамах

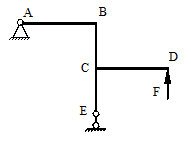
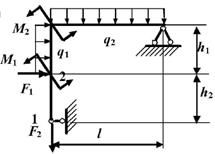
Для рамы (рис.1), соответствующей варианту задания, с размерами и нагрузкой, выбранными по шифру из табл.3, требуется:

1) определить опорные реакции, используя уравнения равновесия;

2) Построить эпюры внутренних силовых факторов М, Q и N;

3) Определить горизонтальное и вертикальное перемещение заданного сечения;

4) Определить угол поворота заданного сечения.

Числовые данные взять из табл.1. Жесткость сечения вертикальных и горизонтальных сечений рамы принять равной EI. Длина каждого из горизонтальных участков l, длина каждого из вертикальных участков h.

Таблица 1

Номер cтроки	Схема по рис.1	F, кН	h, м	l, м	Сечение
01	1	20	1	2	B
02	2	25	2	1	C
03	3	30	3	4	D
04	4	35	4	3	B
05	5	40	5	2	C
06	6	45	1	5	D
07	7	50	2	3	B
08	8	55	3	4	C
09	9	60	4	5	D
10	10	65	5	1	B
11	11	25	3	4	C
12	12	30	4	3	D
13	13	35	5	2	B
14	14	40	1	5	C
15	15	45	2	3	D
16	16	50	3	4	B
17	17	55	2	1	C
18	18	60	3	2	D
19	19	20	2	1	B
20	20	25	1	4	C
21	21	30	3	3	D
22	22	35	2	2	B
23	23	40	2	5	C
24	24	45	3	3	D
25	25	50	4	4	B
26	26	55	5	5	C
27	27	60	1	1	D
28	28	65	2	4	B
29	29	25	3	3	C
30	30	30	4	2	D
31	31	35	5	5	B
32	32	40	3	3	C
33	33	45	4	1	D
34	34	45	5	3	B
35	35	50	1	2	C
36	36	55	2	3	D
	а	б	а	г	в

1 схема 2 схема 3 схема

4 схема 5 схема 6 схема

7 схема 8 схема 9 схема

10 схема 11 схема 12 схема

13 схема 14 схема 15 схема

16 схема 17 схема 18 схема

19 схема 20 схема 21 схема

22 схема 23 схема 24 схема

25 схема 26 схема 27 схема

28 схема 29 схема 30 схема

31 схема 32 схема 33 схема

34 схема 35 схема 36 схема

Рис.1

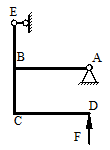
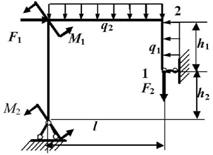
Задача 2. Расчет угловых перемещений в статически определимых консольных рамах

Для рамы (рис.2), соответствующей варианту задания, с размерами и нагрузкой, выбранными по шифру из табл.2, требуется определить угол поворота сечения «К».

Числовые данные взять из табл.2.

Таблица 2

Номер cтроки	Номер схемы по рис.2	F1, кН	М, кНм	q, кН/м	а, м	b, м	l, м
01	1	12	24	5	1	2	2
02	2	10	16	4	2	2	3
03	3	12	12	6	3	2	4
04	4	6	18	2	2	3	2
05	5	8	20	4	1	3	5
06	6	10	12	2	3	1	6
07	7	6	12	3	2	2	3
08	8	8	12	6	1	2	2
09	9	6	16	5	2	1	4
10	10	12	10	6	1	3	3
11	11	11	12	6	1	2	5
12	12	12	18	2	3	3	1
13	13	10	20	4	2	3	2
14	14	12	12	2	1	1	4
15	15	6	12	3	2	2	5
16	16	8	12	6	1	2	3
17	17	10	18	5	2	1	2
18	18	6	20	6	3	2	5
19	19	8	12	2	2	2	3
20	20	6	12	4	1	3	2
21	21	12	12	2	3	3	1
22	22	12	16	3	2	1	3
23	23	13	10	6	1	2	4
24	24	14	12	5	1	2	5
25	25	12	18	6	3	1	3
26	26	10	20	6	2	3	2
27	27	12	12	2	1	2	1
28	28	6	24	4	2	3	3
29	29	8	16	2	1	3	5
30	30	10	12	3	2	1	4
31	31	6	18	6	3	2	2
32	32	8	20	5	2	2	1
33	33	6	12	6	1	1	3
34	34	12	12	2	3	3	6
35	35	11	16	4	2	2	4
36	36	12	12	2	3	3	2
	г	б	б	г	в	а	а

1 схема 2 схема 3 схема

4 схема 5 схема 6 схема

7 схема 8 схема 9 схема

10 схема 11 схема 12 схема

13 схема 14 схема 15 схема

16 схема 17 схема 18 схема

19 схема 20 схема 21 схема

22 схема 23 схема 24 схема

25 схема 26 схема 27 схема

28 схема 29 схема 30 схема

31 схема 32 схема 33 схема

34 схема 35 схема 36 схема

Рис.2

Задача 3. Определение перемещений в статически определимых консольных и двухопорных рамах

Исходные данные к задачам принимаются по табл. 3 и 4 и схемам на рис. 3 и 4.

1. Нарисуйте схему рамы в масштабе. Отрицательные нагрузки направьте в сторону, противоположную показанной на рисунке. Покажите на рисунке размеры рамы и величины нагрузок в численном виде.

2. Найдите опорные реакции и постройте эпюры внутренних усилий N, Q и M. Проверьте равновесие узлов.

3. Определите линейные (вертикальное, горизонтальное) перемещения и угол поворота заданных сечений, используя метод Максвелла - Мора. Для этого:

- приложите в заданных сечениях единичные обобщенные силы, соответствующие искомым перемещениям;

- постройте эпюры изгибающих моментов от единичных сил (M_i);

- выполните перемножение эпюры M изгибающих моментов от заданной нагрузки и эпюр M_i от единичных обобщенных сил, используя правило Верещагина (формулу Симпсона);

- проинтегрируйте формулу Максвелла - Мора аналитически и сравните результаты аналитического и графического (с помощью правила Верещагина, формулы Симпсона) интегрирования формулы Максвелла - Мора.

4. Покажите на рисунке ось рамы после деформации и на ней найденные линейные и угловые перемещения заданных сечений с учетом полученных знаков.

5*.Оцените влияние продольной силы на величину одного из найденных линейных перемещений.

Таблица 3

Номер строки	Схема по рис.3	F1, кН	M1, кНм	l, м	q1, кН/м	q2, кН/м	Линейное перемещение в сечении	F2, кН	M2, кНм	Угол поворота в сечении	h1, м	h2, м
01	1	0	10	5,0	5	0	1	30	0	2	2,0	3,0
02	2	20	0	4,0	0	-5	2	0	-50	1	3,0	2,0
03	3	0	-10	3,0	10	0	1	10	0	2	2,0	4,0
04	4	-20	0	6,0	0	10	2	0	-40	1	4,0	3,0
05	5	0	30	5,0	20	0	1	-20	0	2	4,0	4,0
06	6	-30	0	4,0	0	-20	2	0	-30	1	2,0	2,0
07	7	0	40	3,0	-10	0	1	20	0	2	4,0	2,0
08	8	30	0	4,0	0	20	2	0	-20	1	3,0	4,0
09	9	0	50	6,0	-20	0	1	-30	0	2	4,0	3,0
10	10	-10	0	5,0	0	-10	2	0	-60	1	3,0	3,0
	а	г	в	б	а	г	в	б	а	г	в	б

Таблица 4

Номер строки	Схема по рис.4	q1, кН/м	F1, кН	Линейное перемещение в сечении	q2, кН/м	F2, кН	h1, м	Угол поворота в сечении	M1, кНм	M2, кНм	l, м	h2, м
01	1	10	0	2	0	-10	2,0	1	0	60	3,0	3,0
02	2	0	10	1	20	0	3,0	2	30	0	5,0	4,0
03	3	-10	0	2	0	-20	3,0	1	0	-60	4,0	4,0
04	4	0	20	1	-20	0	2,0	2	-30	0	6,0	4,0
05	5	20	0	2	0	10	4,0	1	0	50	5,0	3,0
06	6	0	-10	1	10	0	4,0	2	40	0	3,0	2,0
07	7	-20	0	2	0	20	3,0	1	0	-50	4,0	2,0
08	8	0	-20	1	-10	0	3,0	2	-40	0	6,0	3,0
09	9	30	0	2	0	-30	2,0	1	0	70	3,0	3,0
10	10	0	30	1	5	0	2,0	2	50	0	5,0	2,0
	в	г	а	б	в	г	а	б	в	г	а	б

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

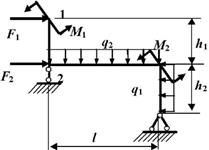
Рис.3

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

Рис. 4

Задача 4. Определение перемещений в статически определимых составных рамах и балках

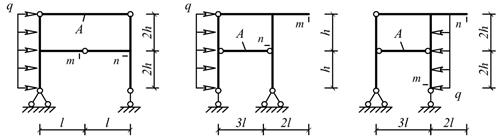
Для одной из рам, изображенных на рис. 5, требуется определить линейное перемещение сечения m и угол поворота сечения n. Расчет перемещений выполнить с учетом податливости сжато-растянутых стержней и упругих связей (пружин). Для расчета принять:

1) жесткость изгибаемых стержней EI постоянной по длине и одинаковой для всех элементов рамы;

2) жесткость сжато-растянутых стержней EA= EI /l²;

3) податливость пружин l³/EI.

Исходные данные для расчета принять из табл.5.

Таблица 5

Номер строки	Схемы балок рис. 5	h, м	l, м	q, кН/м
01	1	4	3.5	2
02	2	3	2.5	3
03	3	1	1.5	4
04	4	1.5	1	1
05	5	2.5	2	8
06	6	3.5	3	3.5
07	7	2	4	7
08	8	2	3	2.5
09	9	3	2.5	1.5
10	10	4	1	3
11	11	1.5	4	4
12	12	2.5	3	1.5
13	13	3	2	2.5
14	14	2	3.5	2
15	15	4	3	3
16	16	1	4	4
17	17	3	3	1
18	18	2	1	2.5
19	19	1	2	1.5
20	20	2	1.5	3
21	21	4	3	3.5
22	22	3	2	2
23	23	2	4	3
24	24	1	2	1
25	25	1.5	1	1.5
26	1	1	3.5	2
27	2	3	2	2.5
28	3	2	3.5	2
29	4	4	3	3
30	5	1	4	4
31	6	3	3	1
32	7	2	1	2.5
33	8	1	2	1.5
34	9	2	1.5	3
35	10	4	3	3.5
36	11	2	3.5	2
	а	г	в	б

Схема 1 Схема 2

Схема 3 Схема 4

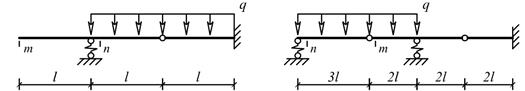
Схема 5 Схема 6

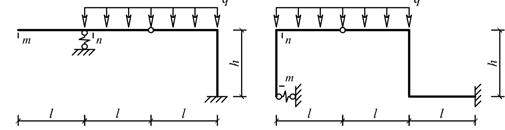
Схема 7 Схема 8

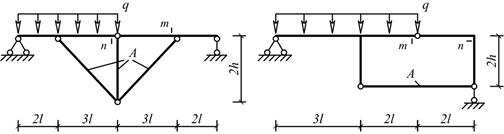
Схема 9 Схема 10

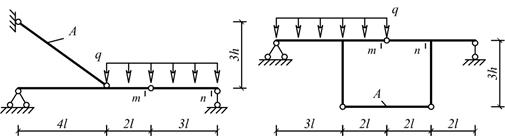
Схема 11 Схема 12

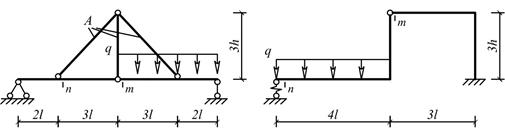
Схема 13 Схема 14

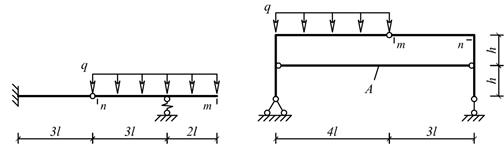
Схема 15 Схема 16

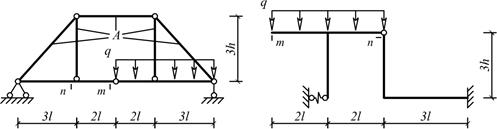
Схема 17 Схема 18

Схема 19 Схема 20 Схема 21

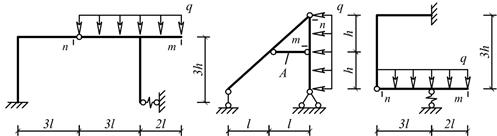
Схема 22 Схема 23 Схема 24

Схема 25

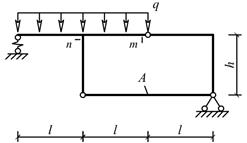
Рис.5

Задача 5. Определение перемещений в статически определимых двухопорных рамах

Для рамы с выбранными из таблицы 6 данными определить горизонтальное перемещение или угол поворота указанного сечения.

В данной задаче жесткости отдельных стержней различны, заданы их соотношения, поэтому искомые перемещения должны быть выражены через EJ₁ или EJ₂.

Особое внимание следует обратить на построение эпюр изгибающих моментов. Прежде чем строить любую эпюру (от нагрузки или единичную), необходимо определить опорные реакции.

Таблица 6

Номер строки	Схемы балок рис. 6	l, м	P, кН	q, кН/м	№ сечения	Вид перемещения	J2:J1
01	1	9,0	9	1,0	1	Угол поворота	1:2
02	2	9,5	2	1,2	2	Горизонтальное перемещение	2:1
03	3	8,0	5	1,5	3	Угол поворота	1:3
04	4	8,5	4	1,8	1	Горизонтальное перемещение	3:1
05	5	5,0	3	2,0	2	Угол поворота	2:3
06	6	5,5	10	2,4	3	Горизонтальное перемещение	3:2
07	7	6,0	7	3,0	1	Угол поворота	3:5
08	8	7,5	8	2,5	2	Горизонтальное перемещение	5:3
09	1	6,8	5	1,9	1	Угол поворота	3:4
10	2	6,2	3	3,2	2	Горизонтальное перемещение	4:3
11	3	6,5	6	3,5	3	Угол поворота	1:2
12	4	9,0	9	1,0	1	Горизонтальное перемещение	2:1
13	5	9,5	2	1,2	2	Угол поворота	1:3
14	6	8,0	5	1,5	3	Горизонтальное перемещение	3:1
15	7	8,5	4	1,8	1	Угол поворота	2:3
16	8	5,0	3	2,0	2	Горизонтальное перемещение	3:2
17	1	5,5	10	2,4	1	Угол поворота	3:5
18	2	6,0	7	3,0	2	Горизонтальное перемещение	5:3
19	3	7,5	8	2,5	3	Угол поворота	3:4
20	4	6,8	5	1,9	1	Горизонтальное перемещение	4:3
21	5	6,2	3	3,2	2	Угол поворота	1:2
22	6	6,5	6	3,5	3	Горизонтальное перемещение	2:1
23	7	9,0	9	1,0	1	Угол поворота	1:3
24	8	9,5	2	1,2	2	Горизонтальное перемещение	3:1
25	1	8,0	5	1,5	1	Угол поворота	2:3
26	2	8,5	4	1,8	2	Горизонтальное перемещение	3:2
27	3	5,0	3	2,0	3	Угол поворота	3:5
28	4	5,5	10	2,4	1	Горизонтальное перемещение	5:3
29	5	6,0	7	3,0	2	Угол поворота	3:4
30	6	7,5	8	2,5	3	Горизонтальное перемещение	4:3
31	7	6,8	5	1,9	1	Угол поворота	1:2
32	8	6,2	3	3,2	2	Горизонтальное перемещение	2:1
33	1	6,5	6	3,5	1	Угол поворота	1:3
34	2	9,0	9	1,0	2	Горизонтальное перемещение	3:1
35	3	9,5	2	1,2	3	Угол поворота	2:3
36	4	8,0	5	1,5	1	Горизонтальное перемещение	3:2
	а	г	в	б	а	в	б

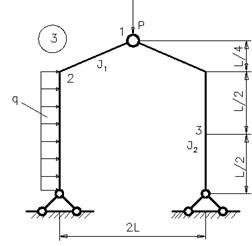
Рис.6. Схемы к задаче 5

Примеры выполнения задач

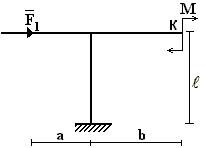
Пример 1

Для рамы, изображенной на рис.7, а, определить горизонтальное перемещение ригеля рамы и угол поворота узла С. Жесткость сечения EI_x, всех элементов рамы одинакова.

F = 50 кН, М = 60 кНм, q = 20 кН/м.

Рис. 7. а) расчетная схема рамы; б)эпюра изгибающих моментов от внешней нагрузки;

в) определение горизонтального перемещения узла «Д»; г) эпюра изгибающих моментов от F = 1;

д) определение угла поворота узла «С»; е) эпюра изгибающих моментов от М = 1

Решение.

Определение перемещений будем выполнять по методу Мора. Интеграл Мора будем вычислять с использованием правила Симпсона. В выражении Влиянием продольных сил на величину перемещений будем пренебрегать, тогда перемещения будем определять по формуле

Строим грузовую эпюру изгибающих моментов от внешней нагрузки M_f (рис.7, б). Для определения горизонтального перемещения ригеля ∆_гор освобождаем раму от внешней нагрузки и прикладываем к раме в узле С или D горизонтальную единичную силу F =1 и строим единичную эпюру (рис. 7, в, г). Вычисляем горизонтальное перемещение ригеля рамы

Знак минус означает, что перемещение ригеля будет вправо, а не влево как предполагали на рис.7, в.

Для определения угла поворота узла С (θ_с) освобождаем раму от внешней нагрузки и прикладываем к раме в узле С единичный момент М =1 и строим единичную эпюру (рис. 7, д, е).

Вычисляем угол поворота узла С. Так как на эпюре на стойках эпюра отсутствует, то перемножение ординат производим только на ригеле

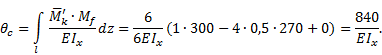
Направление угла поворота совпадает с предполагаемым на рис.7, в и направлено по часовой стрелке.

Пример 2

Определить вертикальное и горизонтальное перемещения сечения В рамы, изображенной на рис.8,а, если жесткость поперечного сечения рамы EI=12000 кНм².

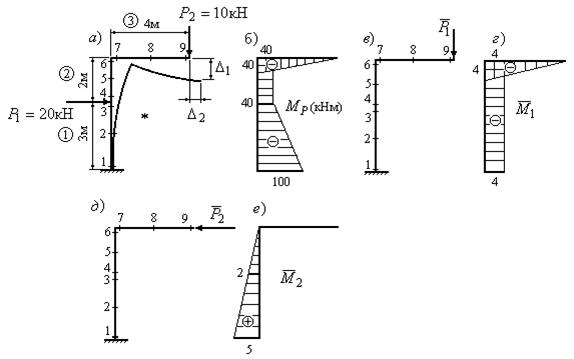
Рис.8

Решение.

1. Разбиваем раму на участки, расставляем характерные сечения и выбираем точку наблюдения (рис.8,а).

2. Определяем грузовые моменты в характерных сечениях и строим эпюру грузовых изгибающих моментов (рис.8,б).

3. Изображаем первое единичное состояние (рис.8,в), определяем моменты в характерных сечениях и строим эпюру единичных изгибающих моментов (рис.8,г).

4. Изображаем второе единичное состояние (рис.8,д), определяем моменты в характерных сечениях и строим эпюру единичных изгибающих моментов (рис.8,е).

5. Находим вертикальное перемещения узла В, перемножая эпюры изгибающих моментов M_P и . Поскольку обе эпюры изгибающих моментов являются линейными, при перемножении эпюр воспользуемся формулами трапеций и треугольников .

На участке №1 будем перемножать эпюры с помощью формулы трапеций, на участках №2 и №3 – с помощью формулы треугольников:

Перемещение получилось положительным. Это означает, что направление перемещения совпадает с направлением единичной силы .

6. Находим горизонтальное перемещение узла В, перемножая эпюры изгибающих моментов M_P и . Так же, как и в предыдущем пункте будем использовать при перемножении эпюр формулы трапеций и треугольников:

Горизонтальное перемещение ∆₂ оказалось отрицательным. Это означает, что узел В в горизонтальном направлении перемещается не влево, куда изначально была направлена единичная сила, а вправо, что соответствует физическому смыслу задачи.

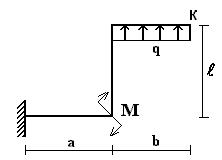
Пример 3

Для рамы, изображенной на рис. 9, требуется определить линейное перемещение сечения m и угол поворота сечения n. Расчет перемещений выполнить с учетом податливости сжато-растянутых стержней и упругих связей (пружин). Для расчета принять:

1) жесткость изгибаемых стержней EI постоянной по длине и одинаковой для всех элементов рамы;

2) жесткость сжато-растянутых стержней EA= EI /l²;

3) податливость пружин l³/EI.

Исходные данные: l=2 м; h=2 м; q=3 кН/м.

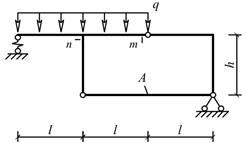
Рис. 9

Решение.

а) Расчетная схема рамы, эпюра изгибающих моментов и значение продольной силы в элементе ab от нагрузки (рис. 10).

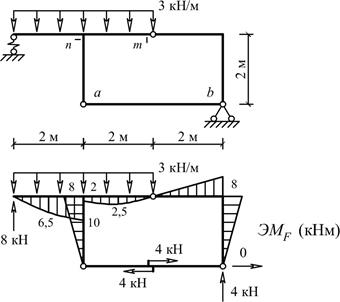
Рис. 10

б) Эпюра изгибающих моментов и значение продольной силы в элементе ab от единичной силы, приложенной в сечении m (рис.11).

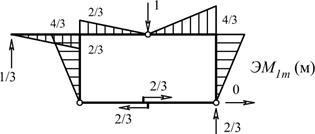
Рис. 11

в) Эпюра изгибающих моментов и значение продольной силы в элементе ab от единичного момента, приложенного в сечении n (рис.12).

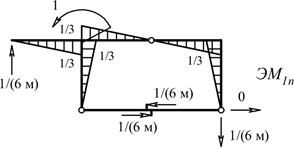
Рис. 12

г) Линейное перемещение сечения m (∆_m) и угловое перемещение сечения n (φ_n), найденные по формуле Мора

д)

где M₁, M_F – эпюра моментов соответственно от единичного воздействия и заданной нагрузки;

N₁, N_F – продольная сила в элементе ab соответственно от единичного воздействия и заданной нагрузки;

R₁, R_F – реакция в пружине соответственно от единичного воздействия и заданной нагрузки.

Пояснения к решению примера 3

1) При построении эпюр изгибающих моментов использован прием, состоящий в том, что предварительно определена продольная сила в сжато-растянутом стержне ab. Для этого было записано выражение изгибающего момента относительно шарнира в отсеченной части, отделенной разрезом от рамы по шарниру и элементу ab, и этот момент приравнен к нулю.

2) В формуле Мора первый член учитывает влияние на величину перемещения изгиба стержней рамы. Для участков с криволинейной эпюрой изгибающих моментов этот член рекомендуется вычислять по формуле Симпсона, т.е.

где (M₁∙M_F)_н, (M₁∙M_F)_с, (M₁∙M_F)_к – произведение значений изгибающих моментов соответственно в начале, середине и конце участка.

На участках с прямолинейной эпюрой M_F вычисление интеграла проще произвести по правилу Верещагина, т.е.

где 𝜔– значений площадь эпюры M_F

у – ордината на эпюре M₁ под (над) центром тяжести эпюры M_F

Второй член формулы Мора учитывает влияние на величину отыскиваемого перемещения податливости сжато-растянутых стержней рамы. Этот член записан в форме решения интеграла Мора для случая, когда N₁ и N_F = const.

3) Третий член в формуле Мора учитывает влияние на величину отыскиваемого перемещения податливости упругих связей (пружин). Он также представлен в форме решения интеграла Мора по аналогии с предыдущим пунктом, если произвести замену N₁ на R₁, N_F на R_F, а вместо EA поставить жесткость пружины EI/L².

Пример 4

Для трехшарнирной рамы, представленной на рис. 13,а необходимо определить

1) опорные реакции и построить эпюры усилий M, Q и N.

2) определить вертикальное перемещение точки (шарнира) С.

Рис.13

Решение.

Опорные реакции определяем с помощью следующих уравнений равновесия:

ΣM_K=0; -8∙3,5+10-3∙4∙2-R_B∙6=0; R_B=-7 кН;

ΣM_B=0; -8∙9,5+10+ R_D∙6-3∙4∙2 =0; R_D=15 кН;

ΣM_С^лев=0; -8∙5,5+10+15∙2+H_A∙4 =0; H_A=1 кН;

ΣM_С^прав=0; 3∙4∙2+7∙4-H_B∙4 =0; H_B=13 кН.

Проверка: ΣX=0; -H_A+H_B-3∙4=0;

ΣY=0; R_D-R_B-8=0.

Для построения эпюр M, Q и N разобьем раму на семь участков (рис.13,б). На участках I - V и VII эпюра М будет линейной, и может быть построена по двум точкам - по концам участков, а эпюры Q и N постоянны и для их построения достаточно определить значения Q и N в любом из сечений участков. На участке VI, на котором действует равномерно распределенная нагрузка, эпюра М будет криволинейной и должна строиться минимум по трем точкам - по краям и в середине участка, а эпюры Q и N будут линейными и их необходимо строить по двум точкам. Все сечения (точки), в которых необходимо вычислять значения М для построения эпюры М показаны на рис. 13,б. Ниже показаны вычисления внутренних усилий в некоторых (наиболее сложных) сечениях:

M₅^лев=1∙2,5-8∙1,5=-9,5 (кНм);

M₇^лев=1∙4-8∙3,5=-24 (кНм);

M₈^лев=1∙4-8∙5,5+15∙2=-10 (кНм);

M₁₀^прав=3∙4∙2-13∙4+7∙2=-14 (кНм);

M₁₂^прав=3∙2∙1-13∙2+7∙2=-6 (кНм);

Q₅^лев=-8∙0,8+1∙0,6=-5,8 (кН);

Q₇=-8+15=+7 (кН);

Q₉^прав=+7 (кН);

Q₁₁^нижн=3∙4-13=-1 (кН);

Q₁₃=-13 (кН);

N₅^лев=+8∙0,6+1∙0,8=5,6 (кН);

N₇^прав=N₈=N₉=N₁₀=-3∙4+13=+1 (кН);

N₁₁^нижн=N₁₂=N₁₃=+7 (кН);

N₁₄^прав=+13 (кН).

После построения эпюр усилий M, Q и N необходимо выполнить проверку равновесия узлов на эпюре М и отдельно по эпюрам Q и N:

а) на эпюре М

ΣM₁=0;

ΣM₂=0;

ΣM₃=0;

ΣM₄=0;

б) по эпюрам Q и N

ΣX=0; -1-5,8∙0,6+5,6∙0,8=0;

ΣY=0; -8-5,8∙0,8+5,6∙0,6=0;

ΣX=0; 1+5,8∙0,6-5,6=0;

ΣY=0; -7-5,8∙0,8-5,6∙0,6+15=0.

Для определения перемещения точки С необходимо в этой точке приложить вертикальную сосредоточенную силу единичной величины, и от ее действия (без учета внешних нагрузок) построить единичную эпюру изгибающих моментов (см. рис. 13,е). Эпюра изгибающих моментов от внешней нагрузки представлена на рис. 13,в. В результате искомое перемещение будет:

Пример 5

Определить горизонтальное перемещение правого узла рамы т. i₁ от нагрузки (рис.14,а).

Рис.14

Решение.

Строим эпюры в заданной раме:

1) от нагрузки эпюру (рис. 14, б);

2) от силы =1, приложенной в т. i₁ по направлению перемещения (рис.14,в).

Эпюры только на двух участках (1), (2). Для упрощения расчетов, представим эпюру на участке (2) в виде двух табличных эпюр (рис. 14,г). Суммарная эпюра двух последних должна быть эквивалентна исходной.

Вычисление перемещения по Верещагину

Здесь знак «-» в скобках при втором слагаемом указывает на то, что перемножаемые эпюры расположены с разных сторон стержня.

Пример 6

Определить угловое перемещение левого узла рамы из примера 5 в т. i₂ от нагрузки (рис. 15).

Рис.15

Решение.

Эпюра от заданной нагрузки приведена на рис. 14, б;

Строим эпюру от единичного момента . Направление момента выбираем произвольно (по часовой стрелке).

Определяем перемещение

Знак «+» говорит о том, что направление углового смещения узла i₂ происходит по выбранному направлению .

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00