Главная

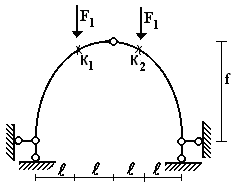
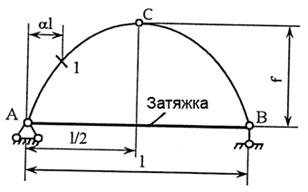
Задача 1. Расчет трехшарнирной арки

Для трехшарнирной арки изображенной на рис.1 требуется определить внутренние усилия в сечениях К₁ и К₂ (уравнение – оси парабола).

Данные взять из табл.1.

Таблица 1

Номер cтроки	Номер схемы по рис.1	F1, кН	q, кН/м	l, м
01	1	12	5	2
02	2	10	4	3
03	3	12	6	4
04	4	6	2	2
05	5	8	4	5
06	6	10	2	6
07	7	6	3	3
08	8	8	6	2
09	9	6	5	4
10	10	12	6	3
11	11	11	6	5
12	12	12	2	1
13	13	10	4	2
14	14	12	2	4
15	15	6	3	5
16	16	8	6	3
17	17	10	5	2
18	18	6	6	5
19	19	8	2	3
20	20	6	4	2
21	21	12	2	1
22	22	12	3	3
23	23	13	6	4
24	24	14	5	5
25	25	12	6	3
26	26	10	6	2
27	27	12	2	1
28	28	6	4	3
29	29	8	2	5
30	30	10	3	4
31	31	6	6	2
32	32	8	5	1
33	33	6	6	3
34	34	12	2	6
35	35	11	4	4
36	36	12	2	2
	а	б	г	в

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

11 схема 12 схема

13 схема 14 схема

15 схема 16 схема

17 схема 18 схема

19 схема 20 схема

21 схема 22 схема

23 схема 24 схема

25 схема 26 схема

27 схема 28 схема

29 схема 30 схема

31 схема 32 схема

33 схема 34 схема

35 схема 36 схема

Рис. 1

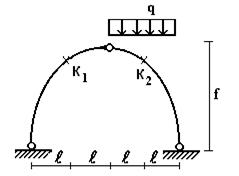
Задача 2. Расчет трехшарнирной арки и рамы с построением линий влияния

Для сплошной трехшарнирной арки или рамы, соответствующей заданному варианту расчетной схемы (рис.2), требуется:

1) построить эпюры изгибающих моментов, поперечных и продольных сил, а также определить значения M, Q, N в сечениях K₁ и K₂ от действия внешней постоянной нагрузки;

2) построить линии влияния M, Q, N от действия подвижной нагрузки для сечений K₁ и K₂ и с помощью линий влияния найти значения M, Q, N от действия внешней постоянной нагрузки.

Исходные данные выбираются из табл. 2.

Таблица 2

Номер cтроки	Номер схемы по рис.2	Очертание оси	l, м	f/l	α	β1	β2	P, кН	q, кН/м
01	а	Парабола	26	0,34	0,20	0,20	0,65	4,0	4,0
02	а	Окружность	36	0,35	0,50	0,30	0,68	3,0	6,0
03	б	Рама	18	0,39	0,30	0,22	0,70	5,0	8,0
04	в	Рама	28	0,40	0,60	0,25	0,72	6,0	5,0
05	г	Рама	20	0,32	0,40	0,15	0,80	7,0	7,0
06	а	Парабола	32	0,36	0,70	0,40	0,84	8,0	4,0
07	а	Окружность	22	0,38	0,80	0,35	0,86	2,0	6,0
08	б	Рама	34	0,33	0,25	0,12	0,75	5,0	8,0
09	в	Рама	24	0,30	0,35	0,33	0,85	8,0	5,0
10	г	рама	30	0,31	0,45	0,45	0,90	4,0	7,0
11	а	Парабола	21	0,21	0,24	0,13	0,66	3,5	3,5
12	а	Окружность	35	0,28	0,65	0,23	0,82	5,5	4,5
13	б	Рама	29	0,25	0,33	0,18	0,73	6,7	5,5
14	в	Рама	23	0,22	0,75	0,14	0,67	7,5	6,5
15	г	Рама	19	0,29	0,42	0,21	0,87	8,5	2,5
16	а	Парабола	31	0,26	0,15	0,19	0,74	2,5	3,5
17	а	Окружность	25	0,23	0,36	0,16	0,69	4,5	4,5
18	б	Рама	37	0,30	0,55	0,26	0,88	6,0	5,5
19	в	Рама	33	0,27	0,27	0,21	0,76	7,0	6,5
20	г	рама	27	0,24	0,48	0,17	0,71	3,0	2,5
21	а	Парабола	20	0,32	0,40	0,15	0,80	7,0	7,0
22	а	Окружность	32	0,36	0,70	0,40	0,84	8,0	4,0
23	б	Рама	22	0,38	0,80	0,35	0,86	2,0	6,0
24	в	Рама	34	0,33	0,25	0,12	0,75	5,0	8,0
25	г	Рама	24	0,30	0,35	0,33	0,85	8,0	5,0
26	а	Парабола	30	0,31	0,45	0,45	0,90	4,0	7,0
27	а	Окружность	21	0,21	0,24	0,13	0,66	3,5	3,5
28	б	Рама	35	0,28	0,65	0,23	0,82	5,5	4,5
29	в	Рама	29	0,25	0,33	0,18	0,73	6,7	5,5
30	г	рама	23	0,22	0,75	0,14	0,67	7,5	6,5
31	а	Парабола	19	0,29	0,42	0,21	0,87	8,5	2,5
32	а	Окружность	31	0,26	0,15	0,19	0,74	2,5	3,5
33	б	Рама	25	0,23	0,36	0,16	0,69	4,5	4,5
34	в	Рама	37	0,30	0,55	0,26	0,88	6,0	5,5
35	г	Рама	33	0,27	0,27	0,21	0,76	7,0	6,5
36	а	Парабола	27	0,24	0,48	0,17	0,71	3,0	2,5
	а	б	в	г	а	б	в	г	а

Рис. 2

Пояснение к решению задачи

На вычерченную в принятом масштабе арку надо нанести все заданные размеры и нагрузку. Для заданных сечений необходимо вычислить координаты и значения синусов и косинусов углов наклона касательных.

Ординаты точек оси арки и углы наклона касательных определяются по следующим уравнениям:

а) при очертании оси по параболе

б) при очертании оси по окружности

где

Для трехшарнирных рам ординаты и необходимые углы наклона определяются непосредственно из чертежа. Следует помнить, что для правой половины арки или рамы угол наклона касательной отрицателен.

Вычисление значений опорных реакций, моментов, поперечных и продольных сил в заданных сечениях надо иллюстрировать необходимыми формулами. На линиях влияния M, Q, N должны быть проставлены числовые значения всех характерных ординат, определение которых должно быть приведено в расчете. Линии влияния надо строить под схемой арки (рамы) в своем линейном масштабе.

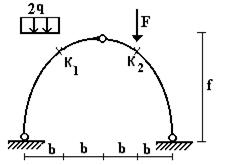
Задача 3. Расчет трехшарнирной арки и рамы с построением линий влияния

Для заданной трехшарнирной арки или рамы (рис. 3) с заданными исходными данными требуется:

1) построить эпюры изгибающих моментов, поперечных и продольных сил и подобрать размеры прямоугольного поперечного сечения из условия прочности по нормальным напряжениям с соотношением b/h согласно шифру;

2) в опасном сечении (установленном в пункте 1) построить линии влияния изгибающих моментов, поперечных и продольных сил.

3) При помощи линий влияния определить внутренние усилия в опасном сечении и сравнить с результатами расчета в п.1).

Исходные данные, согласно шифру, выбираются по табл.3.

Таблица 3

Номер cтроки	Номер схемы по рис.3	q1, кН/м	q2, кН/м	F1, кН	F2, кН	F3, кН	F4, кН	l, м	f, м	b/h
01	1	0	3,2	10	0	0	0	12	4	0,5
02	2	3,8	0	0	0	0	12	24	12	0,3
03	3	0	4,2	0	16	0	0	18	6	0,4
04	4	4,6	0	0	0	24	0	27	10	0,6
05	1	0	4,8	22	0	0	0	12	4	0,5
06	2	4,5	0	0	0	0	20	9	3	0,6
07	3	0	3,4	15	0	0	0	15	5	0,4
08	4	2,8	0	0	0	18	0	18	6	0,5
09	1	0	3,0	0	14	0	0	24	12	0,4
10	2	2,6	0	0	0	25	0	12	6	0,6
11	1	0	3,2	10	0	0	0	12	4	0,5
12	2	3,8	0	0	0	0	12	24	12	0,3
13	3	0	4,2	0	16	0	0	18	6	0,4
14	4	4,6	0	0	0	24	0	27	10	0,6
15	1	0	4,8	22	0	0	0	12	4	0,5
16	2	4,5	0	0	0	0	20	9	3	0,6
17	3	0	3,4	15	0	0	0	15	5	0,4
18	4	2,8	0	0	0	18	0	18	6	0,5
19	1	0	3,0	0	14	0	0	24	12	0,4
20	2	2,6	0	0	0	25	0	12	6	0,6
21	1	0	3,2	10	0	0	0	12	4	0,5
22	2	3,8	0	0	0	0	12	24	12	0,3
23	3	0	4,2	0	16	0	0	18	6	0,4
24	4	4,6	0	0	0	24	0	27	10	0,6
25	1	0	4,8	22	0	0	0	12	4	0,5
26	2	4,5	0	0	0	0	20	9	3	0,6
27	3	0	3,4	15	0	0	0	15	5	0,4
28	4	2,8	0	0	0	18	0	18	6	0,5
29	1	0	3,0	0	14	0	0	24	12	0,4
30	2	2,6	0	0	0	25	0	12	6	0,6
31	1	0	3,2	10	0	0	0	12	4	0,5
32	2	3,8	0	0	0	0	12	24	12	0,3
33	3	0	4,2	0	16	0	0	18	6	0,4
34	4	4,6	0	0	0	24	0	27	10	0,6
35	1	0	4,8	22	0	0	0	12	4	0,5
36	2	4,5	0	0	0	0	20	9	3	0,6
	б	а	г	в	в	б	г	а	г	в

Схемы нагрузки

Рис. 3. Расчетные схемы распорных систем и схемы нагрузки

Пояснение к решению задачи

Схему арки надо вычертить, определив по уравнению ее оси достаточное число точек (не менее шести, включая замковый шарнир) и проведя через них плавную кривую. На схему надо нанести все заданные размеры и нагрузку. Для отмеченных сечений надо вычислить координаты и, кроме того, значения синусов и косинусов углов наклона касательных и составить таблицу геометрических характеристик.

На вычерченную в принятом масштабе арку надо нанести все заданные размеры и нагрузку. Для заданных сечений необходимо вычислить координаты и значения синусов и косинусов углов наклона касательных.

Ординаты точек оси арки и углы наклона касательных определяются по следующим уравнениям:

а) при очертании оси по параболе

б) при очертании оси по окружности

где

Для трехшарнирных рам ординаты и необходимые углы наклона определяются непосредственно из чертежа. Следует помнить, что для правой половины арки или рамы угол наклона касательной отрицателен.

Вычисление значений опорных реакций, моментов, поперечных и продольных сил в заданных сечениях надо иллюстрировать необходимыми формулами. На линиях влияния M, Q, N должны быть проставлены числовые значения всех характерных ординат, определение которых должно быть приведено в расчете. Линии влияния надо строить под схемой арки (рамы) в своем линейном масштабе.

Вычисление значений опорных реакций, моментов, поперечных и продольных сил в заданных точках надо иллюстрировать необходимыми формулами.

Опасным принято называть сечение, в котором напряжения достигает наибольших (наименьших) значений. Напряжения определяются по формулам внецентренного сжатия

В формуле для определения напряжений А – площадь поперечного сечения арки или рамы, а W – осевой момент сопротивления сечения.

Следовательно, положение "опасного" сечения определяется комбинацией М, N и находится по соответствующим эпюрам. Для "опасных" сечений требуется построить эпюры нормальных напряжений. При этом сечение принимается постоянным по длине арки и является прямоугольным с отношением b/h согласно таблице 3.

Выбрав "опасное" сечение " К ", необходимо построить линии влияния М_k,, Q_k и N_к. Для построения линий влияния М_k,, Q_k и N_к. надо сначала построить линию влияния распора и подсчитать значение ее характерной ординаты. На окончательных линиях влияния должны быть проставлены числовые значения всех характерных ординат, определение которых должно быть приведено в расчете.

Линии влияния надо строить под схемой арки (рамы) в том же линейном масштабе. Загрузив линии влияния заданной нагрузкой, найти величину усилий в опасном сечении и составить таблицу сравнения результатов пунктов 1 и 3.

Задача 4. Расчет трехшарнирной арки с построением линий влияния

Для трехшарнирной арки с заданными исходными данными требуется:

1) Определить аналитически опорные реакции от заданной нагрузки.

2) Аналитическим способом построить эпюры изгибающих моментов, поперечных и продольных сил от заданной нагрузки.

3) Построить линии влияния изгибающего момента, поперечной и продольной силы для заданного сечения k₁ и k₂.

4) Подсчитать по линиям влияния для сечения k₁ и k₂ величины внутренних усилий (M, Q и N).

5) Сравнить величины внутренних усилий M, Q и N для сечения k₁ и k₂, полученные по линиям влияния, с их величинами, определенными аналитически.

6) Провести расчет трехшарнирной арки на заданную нагрузку на ЭВМ.

Исходные данные, согласно шифру, выбираются по табл. 4.

Таблица 4

Номер cтроки	Очертание оси арки	l, м	а1, м	а2, м	b1, м	b2, м	q1, кН/м	q2, кН/м	f, м	P1, кН	P2, кН
01	парабола	26	5	10	17	5	–	40	9	40	100
02	окружность	36	10	7	25	10	40	–	12	50	90
03	парабола	18	7	2	12	4	–	50	6	60	70
04	окружность	28	7	8	20	7	50	–	11	70	60
05	парабола	20	6	4	16	3	–	60	6	80	50
06	окружность	32	3	8	27	13	60	–	12	90	40
07	парабола	22	4	8	19	8	70	–	8	100	40
08	окружность	34	12	10	25	4	–	70	11	90	50
09	парабола	24	10	10	20	8	80	–	7	80	40
10	окружность	30	13	9	24	13	–	80	9	70	50
11	парабола	26	5	10	17	5	–	40	9	40	100
12	окружность	36	10	7	25	10	40	–	12	50	90
13	парабола	18	7	2	12	4	–	50	6	60	70
14	окружность	28	7	8	20	7	50	–	11	70	60
15	парабола	20	6	4	16	3	–	60	6	80	50
16	окружность	32	3	8	27	13	60	–	12	90	40
17	парабола	22	4	8	19	8	70	–	8	100	40
18	окружность	34	12	10	25	4	–	70	11	90	50
19	парабола	24	10	10	20	8	80	–	7	80	40
20	окружность	30	13	9	24	13	–	80	9	70	50
21	парабола	26	5	10	17	5	–	40	9	40	100
22	окружность	36	10	7	25	10	40	–	12	50	90
23	парабола	18	7	2	12	4	–	50	6	60	70
24	окружность	28	7	8	20	7	50	–	11	70	60
25	парабола	20	6	4	16	3	–	60	6	80	50
26	окружность	32	3	8	27	13	60	–	12	90	40
27	парабола	22	4	8	19	8	70	–	8	100	40
28	окружность	34	12	10	25	4	–	70	11	90	50
29	парабола	24	10	10	20	8	80	–	7	80	40
30	окружность	30	13	9	24	13	–	80	9	70	50
31	парабола	26	5	10	17	5	–	40	9	40	100
32	окружность	36	10	7	25	10	40	–	12	50	90
33	парабола	18	7	2	12	4	–	50	6	60	70
34	окружность	28	7	8	20	7	50	–	11	70	60
35	парабола	20	6	4	16	3	–	60	6	80	50
36	окружность	32	3	8	27	13	60	–	12	90	40
	б	а	г	в	в	б	г	а	г	в

Рис. 4. Схема арки

Задача 5. Расчет трехшарнирной арки и рамы с построением линий влияния с построением линий влияния

Для сплошной трёхшарнирной арки или рамы (рис.5.) требуется:

1) Провести кинематический анализ;

2) Построить эпюры изгибающих моментов, поперечных и нормальных сил от действия постоянной нагрузки (рис.6);

3) Построить линии влияния M, Q и N для сечения 1 и по ним найти значения M, Q и N от той же постоянной нагрузки. Сравнить полученный результат c аналитическим расчетом.

Исходные данные, согласно шифру, выбираются согласно табл. 5.

Таблица 5

Номер cтроки	Номер схемы по рис.5	Очертание оси арки	l, м	f/l	α	q1, кН/м	q2, кН/м	P, кН
01	1	Парабола	24	0,34	0,20	0	4	4,0
02	2	Окружность	36	0,35	0,50	4	0	3,0
03	3	Парабола	18	0,39	0,30	0	5	5,0
04	4	Окружность	28	0,40	0,60	5	0	6,0
05	5	Парабола	20	0,32	0,40	0	6	7,0
06	6	Окружность	32	0,36	0,70	6	0	8,0
07	7	Парабола	22	0,38	0,80	7	0	2,0
08	8	Окружность	34	0,33	0,25	0	7	5,0
09	9	Парабола	24	0,30	0,35	8	0	8,0
10	10	Окружность	30	0,31	0,45	0	8	4,0
11	1	Парабола	24	0,21	0,24	0	4	3,5
12	2	Окружность	36	0,28	0,65	4	0	5,5
13	3	Парабола	18	0,25	0,33	0	5	6,7
14	4	Окружность	28	0,22	0,75	5	0	7,5
15	5	Парабола	20	0,29	0,42	0	6	8,5
16	6	Окружность	32	0,26	0,15	6	0	2,5
17	7	Парабола	22	0,23	0,36	7	0	4,5
18	8	Окружность	34	0,30	0,55	0	7	6,0
19	9	Парабола	24	0,27	0,27	8	0	7,0
20	10	Окружность	30	0,24	0,48	0	8	3,0
21	1	Парабола	24	0,32	0,40	0	4	7,0
22	2	Окружность	36	0,36	0,70	4	0	8,0
23	3	Парабола	18	0,38	0,80	0	5	2,0
24	4	Окружность	28	0,33	0,25	5	0	5,0
25	5	Парабола	20	0,30	0,35	0	6	8,0
26	6	Окружность	32	0,31	0,45	6	0	4,0
27	7	Парабола	22	0,21	0,24	7	0	3,5
28	8	Окружность	34	0,28	0,65	0	7	5,5
29	9	Парабола	24	0,25	0,33	8	0	6,7
30	10	Окружность	30	0,22	0,75	0	8	7,5
31	1	Парабола	24	0,29	0,42	0	4	8,5
32	2	Окружность	36	0,26	0,15	4	0	2,5
33	3	Парабола	18	0,23	0,36	0	5	4,5
34	4	Окружность	28	0,30	0,55	5	0	6,0
35	5	Парабола	20	0,27	0,27	0	6	7,0
36	6	Окружность	32	0,24	0,48	6	0	3,0
	а	б	в	г	а	б	в	г

1 схема

2 схема

3 схема

4 схема

5 схема

6 схема

7 схема

8 схема

9 схема

10 схема

Рис.5

Рис.6. Схема нагрузки

Пояснение к решению задачи

Схему арки надо вычертить, определив по уравнению её оси не менее пяти точек, включая замковый шарнир C и проведя через них плавную кривую. На схему надо нанести все заданные размеры и нагрузки.

Ординаты точек оси арки и углы наклона касательных определяются по следующим уравнениям:

а) при очертании оси по параболе:

где f - стрела подъема

б) при очертании оси по окружности:

где

Для трёхшарнирных рам ординаты и необходимые углы наклона определяются непосредственно из чертежа.

Для построения эпюр М, Q и N ось арки или рамы следует разбить на участки c равными проекциями (не менее восьми участков). В число расчётных точек необходимо включить точку приложения силы Р, начало и конец распределённой нагрузки, шарнир С и сечение 1, a для рам точки, в которых изменяется угол наклона оси рамы.

Вычисление значений опорных реакций, моментов, поперечных и нормальных сил в расчётных точках надо иллюстрировать необходимыми формулами.

При построении линий влияния М, Q и N в сечении 1 на них должны быть проставлены числовые значения всех характерных ординат. Линии влияния надо строить под схемой арки (рамы) в том же линейном масштабе.

Примеры расчета трехшарнирной арки

Пример 1.

1. Определение опорных реакций от заданной нагрузки

Проведем расчет арки, показанной на рис. 7, а.

При действии на арку вертикальной нагрузки возникают две вертикальные опорные реакции R_A и R_B, и горизонтальная опорная реакция Н, называемая распором (см. рис.7, а). Указанные опорные реакции определяются из 3 уравнений статики:

1. Равенство нулю суммы моментов всех сил относительно шарнира В, из которого определяется опорная реакция R_A.

2. Равенство нулю суммы моментов всех сил относительно шарнира А, из которого определяется опорная реакция R_В.

3. Равенство нулю суммы моментов сил, приложенных к левой или правой половине арки, относительно ключевого шарнира С, из которого определяется распор Н.

R_A = 39 кН.

R_B = 37 кН.

H=36 kH.

Проверка правильности вычисления опорных реакций осуществляется по формулам:

2. Определение внутренних усилий в сечениях арки

Для получения формулы уравнений внутренних усилий в сечении применяется метод плоских сечений. При этом рассматривается равновесие левой отсеченной части арки относительно сечения. При расстоянии равном х от рассматриваемого сечения до опоры А (см. рис. 7, а), получим:

(1)

(2)

(3)

где – балочный изгибающий момент и балочная поперечная сила в сечении х балки пролетом l от приложенной к балке внешней нагрузки (см. рис. 7, б‑г), y_x, cosφ_x, sinφ_x – геометрические параметры, определяемые по следующим уравнениям:

а) при очертании оси по параболе

б) при очертании оси по окружности

где

Следует помнить, что для правой половины арки угол φ_x отрицательный.

Таким образом, для построения эпюр внутренних усилий необходимо:

– Отметить на оси арки достаточное число точек (не менее пяти, включая шарнир С).

– Вычислить координаты, значения синусов и косинусов углов наклона касательных всех этих точек.

– Найти значения изгибающего момента и поперечной силы для соответствующих точек балки, загруженной той же нагрузкой, что и арка.

– По формулам (1) – (3) вычислить значения внутренних усилий в арке.

Приведенную последовательность действий удобнее всего выполнять в таблице 6

Таблица 6

№ п/п	Координата, м		tg φx	cos φx	sin φx	, кНм	, Кн	Mx, кНм	Qx, кН	Nx, кН
	x	yx
1	0	0,000	1,000	0,707	0,707	0	39	0,000	2,121	-53,033
2	3	2,625	0,750	0,800	0,600	108	33	13,500	4,800	-48,600
							21		-4,800	-41,400
3	6	4,500	0,500	0,894	0,447	162	15	0,000	-2,683	-38,908
4	9	5,625	0,250	0,970	0,243	198	9	-4,500	0,000	-37,108
5	12	6,000	0,000	1,000	0,000	216	3	0,000	3,000	-36,000
6	15	5,625	-0,250	0,970	-0,243	211,5	-6	9,000	2,910	-36,380
							-10		-0,970	-37,350
7	18	4,500	-0,500	0,894	-0,447	168	-19	6,000	-0,894	-40,696
8	21	2,625	-0,750	0,800	-0,600	97,5	-28	3,000	-0,800	-45,600
9	24	0,000	-1,000	0,707	-0,707	0	-37	0,000	-0,707	-51,619

Эпюры внутренних усилий в арке показаны на рис. 7, д-ж.

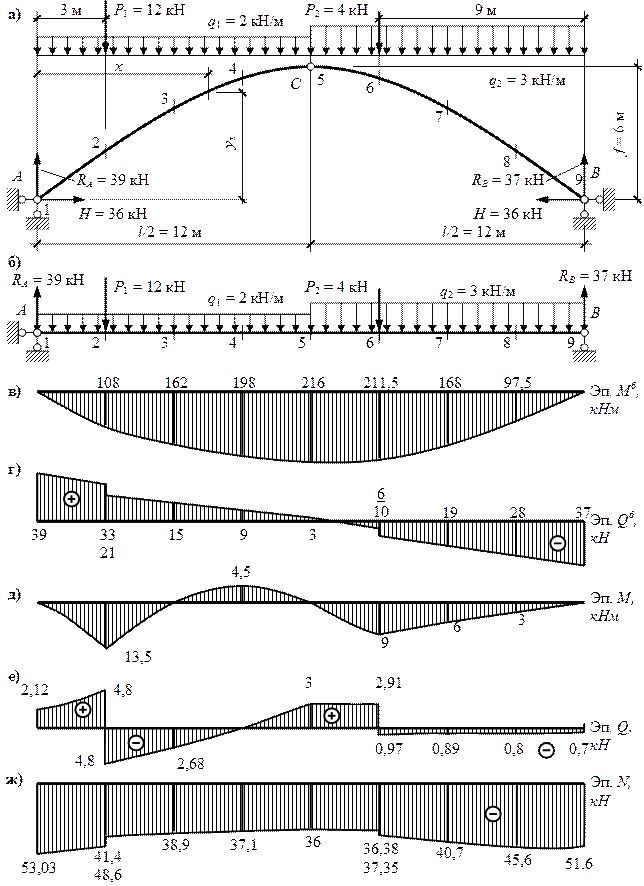
Рис. 7. Пример расчета на неподвижную нагрузку

3. Построение линий влияния в трехшарнирных арках

3.1. Линии влияния опорных реакций

Приведем формулы вертикальных опорных реакций, которые будут необходимы для вывода аналитических выражений М, Q, N и построения их линий влияния. При принятой системе координат (рис. 8, а) аналитическое выражения R_A и R_B найдем соответственно из выражений:

откуда при Р = 1

Вычисляем численные значения R_A и R_B:

при x=0, R_A =0, R_B =1;

при x=l, R_A =1, R_B =0.

Линии влияния опорных реакций показаны на рис. 8, б, в.

3.2.Линии влияния распора H

Получим аналитическое выражение правой ветви линии влияния распора, для этого примем, что Р = 1 находится правее сечения С, 0 ≤ x ≤ l/2

Из уравнения равновесия

Находим

Вычисляем численные значения распора:

при х = 0 Н = 0;

Для получения аналитического выражения левой ветви линии влияния Н примем, что P=1 левее сечения С; l/2 ≤ x ≤ l.

Откуда

Характерные ординаты левой ветви

при х = l Н = 0.

Линия влияния распора, ее характерные ординаты и формулы построения левой и правой ветви, показаны на рис. 8, г.

3.3. Линии влияния изгибающего момента М_k, поперечной силы Q_k, продольной силы N_k в сечении k, находящемся левее ключевого шарнира

1. Примем P=1 левее сечения k;

b ≤ x ≤ l;

Рассмотрим равновесие правой отсеченной части.

Изгибающий момент в сечении k

а характерные ординаты его линии влияния равны:

при х = l M_k = 0;

при х = b

Поперечная сила в сечении k

а ее характерные ординаты равны

при х = l Q_k = 0;

при х = b

Продольная сила в сечении k

Характерные ординаты продольной силы равны

при х = l N_k = 0;

при х = b

2. Примем P=1 правее сечения k;

l/2 ≤ x ≤ b

При этих условиях:

При х = b

при х = l/2

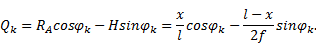
При х = b

при х = l/2

При х = b

при х = l/2

3. Примем Р=1 между точками С и B;

0 ≤ x ≤ l/2, .

При этих условиях

При х = l/2

при х = 0 M_k = 0.

При х = l/2

при х = 0 Q_k = 0.

При х = l/2

при х = 0 N_k = 0.

Линии влияния изгибающего момента, поперечной и продольной сил показаны соответственно на рис. 8., д, е, ж.

Рассматривая эти линии влияния, можно заметить, что для их построения следует вычислить следующие основные ординаты внутренних усилий при положении подвижной единичной нагрузки:

– чуть левее сечения k;

– чуть правее сечения k;

– над ключевым шарниром.

Формулы для определения значений этих ординат приведены в табл. 7.

Рис. 8. Построение линий влияния в трехшарнирной арке

Таблица 7. Значения основных вершин на линиях влияния

Наименование вершины (см. рис. 8)	Формулы
	Сечение k левее шарнира С	Сечение k правее шарнира С*
ИЗГИБАЮЩИЙ МОМЕНТ
hC (Р = 1 на шарнире С)
hk (Р = 1 на сечении k)
ПОПЕРЕЧНАЯ СИЛА
aC (Р = 1 на шарнире С)
(Р = 1 чуть левее сечения k)
(Р = 1 чуть правее сечения k)
ПРОДОЛЬНАЯ СИЛА
bc (Р = 1 на шарнире С)
(Р = 1 чуть левее сечения k)
(Р = 1 чуть правее сечения k)

* – напомним, что если сечение находится правее шарнира С, то sinφ_k отрицательный.

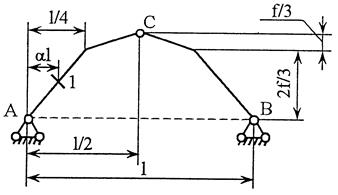
4. Пример построения линий влияния внутренних усилий в сечении k₁, расположенном левее ключевого шарнира С

Геометрические характеристики арки (см. рис. 9, а):

- ось арки – квадратная парабола;

- пролет l = 24 м;

- стрела подъема f = 6 м;

Геометрические характеристики сечения k₁:

- a = 3 м;

- b = 21 м;

- y_k1 = 2,625 м;

- sinφ _k1 = 0,6;

- cosφ _k1 = 0,8.

4.1. Построение линии влияния изгибающего момента M_k1

Определяем характерные ординаты линии влияния.

1. Сила Р = 1 на сечении k.

2. Сила Р = 1 на шарнире С.

Соединяя полученные ординаты прямыми линиями между собой и с нулевыми ординатами линии влияния на опорах, получим линию влияния изгибающего момента в сечении k₁ (см. рис. 9, б).

Рис. 9. Пример построения линий влияния

4.2. Построение линии влияния поперечной (Q_k1) и продольной (N_k1) сил

Определяем характерные ординаты линии влияния.

1. Сила Р = 1 чуть левее сечения k.

2. Сила Р = 1 чуть правее сечения k.

3. Сила Р = 1 на шарнире С.

Соединяя полученные ординаты прямыми линиями между собой и с нулевыми ординатами линии влияния на опорах, получим линию влияния поперечной и продольной сил в сечении k₁ (см. рис. 9, в, г).

5. Пример построения линий влияния внутренних усилий в сечении k₂, расположенном правее ключевого шарнира С

Геометрические характеристики сечения k₂ (см. рис. 7, а):

– a = 15 м;

– b = 9 м;

– y_k1 = 5,625 м;

– sinφ _k1 = –0,243;

– cosφ _k1 = 0,97.

5.1. Построение линии влияния изгибающего момента M_k2

Определяем характерные ординаты линии влияния.

1. Сила Р = 1 на сечении k.

2. Сила Р = 1 на шарнире С.

Соединяя полученные ординаты прямыми линиями между собой и с нулевыми ординатами линии влияния на опорах, получим линию влияния изгибающего момента в сечении k₂ (см. рис. 10, б).

Рис. 10. Пример построения линий влияния

5.2. Построение линии влияния поперечной (Q_k2) и продольной (N_k2) сил

Определяем характерные ординаты линии влияния.

1. Сила Р = 1 чуть левее сечения k.

2. Сила Р = 1 чуть правее сечения k.

3. Сила Р = 1 на шарнире С.

Соединяя полученные ординаты прямыми линиями между собой и с нулевыми ординатами линии влияния на опорах, получим линию влияния поперечной и продольной сил в сечении k₂ (см. рис. 10, в, г).

5.3. Определение усилий по линиям влияния от заданной нагрузки

При действии на балку системы сил Р₁, Р₂ … Р_n равномерно распределенных нагрузок q₁, q₂ … q_n и моментов М₁, М₂ … М_n полное усилие получим по принципу сложения действий:

где n – соответственное количество нагрузок Р_i, q_i, М_i; y_i – ордината линий влияния определяемого усилия под действием силы Р_i; ω_i – площадь участка линии влияния под нагрузкой q_i; α_i – угол наклона линии влияния в точке приложения момента М_i.

5.4. Усилия M_k1, N_k1 и Q_k1 в сечении k₁ по линиям влияния от заданной нагрузки

При действии заданной нагрузки (см. рис. 8, а) изгибающий момент в сечении определится по формуле:

Ордината на линии влияния M_k1 под силой Р₁: y₁ = 1,97 м.

Ордината на линии влияния M_k1 под силой Р₂ определится из пропорции: , откуда

Площадь участка линии влияния M_k1 под нагрузкой q₁:

Площадь участка линии влияния M_k1 под нагрузкой q₂:

Момент в сечении k₁:

Момент в сечении k₁, определенный аналитически (рис. 7): M_k1 = 13,5 кНм.

Рис. 10. Определение усилий по линиям влияния в сечении k₁

Разница в значениях момента составляет , что менее предельной ошибки [3%], и обусловлена округлениями при подсчетах.

Поперечная сила в сечении k₁ определится по той же формуле:

При определении значения y₁ замечаем, что сила Р₁ находится как раз в сечении k₁ и в этом месте происходит скачек значений на линии влияния Q_k1. Из двух значений выбираем любое, например y₁ = 0,55 (определяем поперечную силу чуть левее сечения).

Ордината на линии влияния Q_k1 под силой Р₂ определится из пропорции: , откуда .

Поперечная сила в сечении k₁:

Поперечная сила в сечении k₁, определенная аналитически: Q_k1 = 4,8 кН. Значения совпадают.

Аналогично определим по линии влияния продольную силу в сечении k₁.

Поперечная сила в сечении k₁, определенная аналитически: N_k1 = –48,6 кН. Значения совпадают.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00