Главная

Задача 1. Расчет перемещений в рамах от изменения температуры

Для одной из рам, изображенных на рис. 1, требуется определить линейное перемещение сечения m и угол поворота сечения n.

При расчете перемещений принять:

1) высоту поперечного сечения всех стержней h_c=0,1l;

2) положение центра тяжести поперечного сечения посередине его высоты;

3) коэффициент линейного расширения одинаковым для всех элементов системы и равным α = 10^-5 1/град;

4) параметр температуры t = 10°C (на схемах рам температура снаружи t_н не показана).

Исходные данные принять из табл. 1.

Таблица 1

Номер строки	Схемы балок по рис. 1	l, м	h, м	Температура снаружи, tн	Температура внутри, tв
01	1	2	2.5	t	-2t
02	2	3	4	-t	-3t
03	3	4	3	2t	4t
04	4	2	3	-2t	4t
05	5	2	4	4t	-4t
06	6	4	2.5	3t	-t
07	7	3	4	-3t	t
08	8	2	3	-2t	2t
09	9	1	2.5	t	3t
10	10	2	1.5	-t	-3t
11	11	4	3	2t	2t
12	12	3	4	3t	-2t
13	13	2	2.5	-3t	t
14	14	1	2	t	-t
15	15	3	3	-2t	2t
16	16	4	4	-t	-4t
17	17	3	2.5	3t	-t
18	18	1	4	4t	2t
19	19	2	3	-t	4t
20	20	2	4	-2t	3t
21	21	3	2.5	3t	-t
22	22	2	3.5	2t	3t
23	23	4	3	3t	2t
24	24	2	3.5	-t	4t
25	25	1	2.5	2t	-2t
	в	г	б	а	в

Схема 1 Схема 2 Схема 3

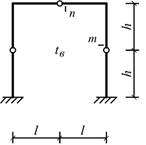
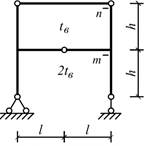
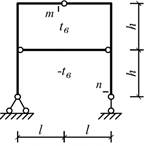
Схема 4 Схема 5 Схема 6

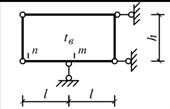
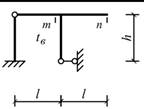
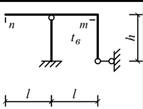
Схема 7 Схема 8 Схема 9

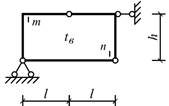
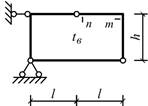
Схема 10 Схема 11 Схема 12

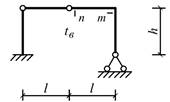
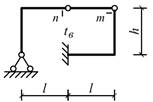
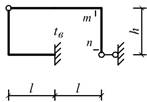
Схема 13 Схема 14 Схема 15

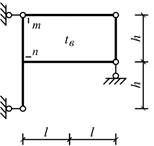
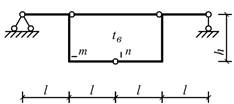
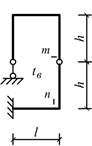
Схема 16 Схема 17 Схема 18

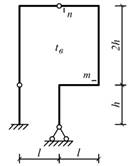
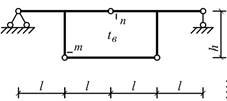
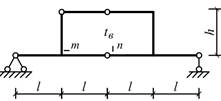
Схема 19 Схема 20 Схема 21

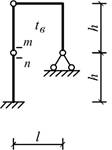
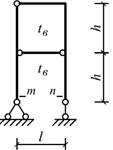
Схема 22 Схема 23 Схема 24

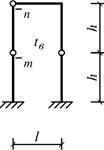
Схема 25

Рис.1

Примеры выполнения задач

Пример 1.

Исходные данные: схема рамы на рис.2; l=2 м; h=2 м; t_н= t; t_в= -4t; l=2 м; t=10°C.

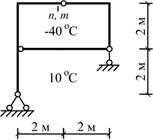
Рис.2

Решение.

1) Эпюры изгибающих моментов и продольной силы в раме от единичной силы, приложенной в сечении m (для определения вертикального перемещения сечения m) (рис.3).

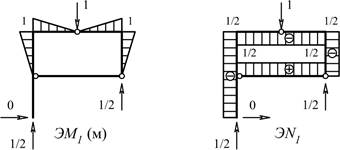
Рис.3

2) Эпюры изгибающих моментов и продольной силы в раме от единичного момента, приложенного в сечении n (для определения угла поворота сечения n) (рис.4).

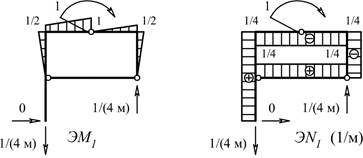
Рис.4

3) Линейное (Δ_m) перемещение сечения m и угловое (φ_n) перемещение сечения n, найденные по формуле Мора

где α – коэффициент линейного расширения;

t’=( t_н + t_в)/2 – температура на оси стержня;

t’’=| t_н - t_в |;

ω_N1, ω_M1 – площадь эпюры соответственно N₁ и M₁ на участке (стержне).

Примечания.

- В формуле Мора первый член учитывает влияние температурного удлинения (укорочения) стержней рамы на величину отыскиваемого перемещения, а второй член – влияние на перемещение температурного искривления стержней.

- Знак первого члена формулы Мора устанавливается в зависимости от знака температуры на оси стержня (t’) и знака эпюры продольной силы; знак второго члена зависит от направления температурной кривизны и кривизны от изгиба, вызванного единичной силой. Если на каком-либо участке эти кривизны совпадают, то знак второго члена принимается положительным, в противном случае – отрицательным.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00