Главная

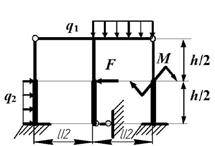
Задача 1. Расчет статически неопределимых рам методом сил

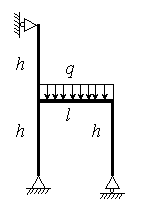
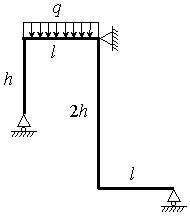
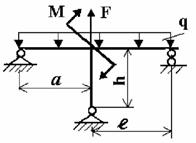
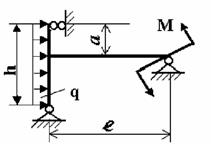
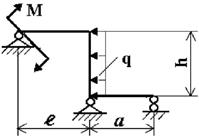
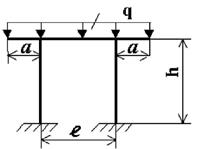
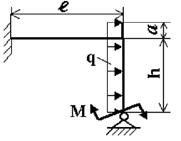
На рис. 1 изображена нагруженная в своей плоскости рама, вертикальные элементы которой имеют моменты инерции j, а горизонтальные элементы kj.

Требуется:

1. установить степень статической неопределимости и выбрать основную систему;

2. написать канонические уравнения;

3. построить эпюру М от единичных сил и от заданной нагрузки;

4. найти коэффициент канонических уравнений;

5. найти величины «лишних» неизвестных Х;

6. выполнить деформационную проверку правильности определения неизвестных;

7. построить окончательные эпюры внутренних силовых факторов N, Q_y, M_x.

Указание. При выполнении деформационной проверки следует установить, равняется ли нулю перемещение одной из опорных точек. Для этого необходимо выбрать новую основную систему, приложить в направлении отброшенной связи единичную силу, построить эпюру моментов. Перемножив эпюру моментов от внешней нагрузки и от найденной неизвестной силы Х на эпюру моментов от единичной нагрузки, определить перемещение опорной точки. При правильно решенной задаче в результате перемножения должен получиться ноль.

Данные взять из табл. 1.

Таблица 1

Номер cтроки	Схема по рис.1	l, м	h, м	k	q, кН/м
01	1	11	2	1,1	15
02	2	12	3	1,2	20
03	3	3	4	1,3	30
04	4	4	5	1,4	4
05	5	5	6	1,5	5
06	6	6	2	1,6	6
07	7	7	3	1,7	7
08	8	8	4	1,8	8
09	9	9	5	1,9	9
10	10	10	6	2,0	10
11	11	5	5	1,4	30
12	12	6	6	1,5	4
13	13	7	2	1,6	5
14	14	8	3	1,7	6
15	15	9	4	1,8	7
16	16	11	5	1,1	8
17	17	12	4	1,2	30
18	18	3	5	1,3	4
19	19	4	6	1,4	5
20	20	5	2	1,5	6
21	21	6	3	1,6	7
22	22	7	4	1,7	8
23	23	8	5	1,8	9
24	24	9	6	1,9	10
25	25	10	5	2,0	30
26	26	5	6	1,4	4
27	27	6	2	1,5	5
28	28	7	3	1,6	6
29	29	8	4	1,7	7
30	30	9	5	1,8	15
31	31	5	2	1,5	20
32	32	6	3	1,6	30
33	33	7	4	1,7	4
34	34	8	5	1,8	5
35	35	9	6	1,1	6
36	36	10	3	1,2	7
	б	а	г	в	а

1 схема 2 схема 3 схема

4 схема 5 схема 6 схема

7 схема 8 схема 9 схема

10 схема 11 схема 12 схема

13 схема 14 схема 15 схема

16 схема 17 схема 18 схема

19 схема 20 схема 21 схема

22 схема 23 схема 24 схема

25 схема 26 схема 27 схема

28 схема 29 схема 30 схема

31 схема 32 схема 33 схема

34 схема 35 схема 36 схема

Рис.1

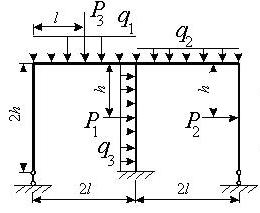
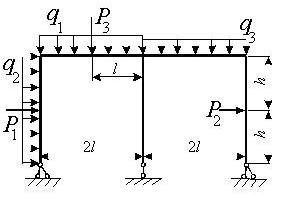
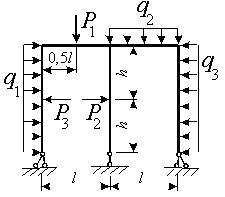
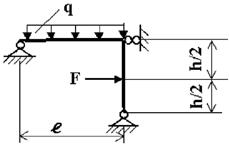
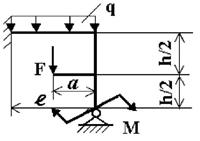
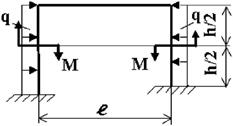
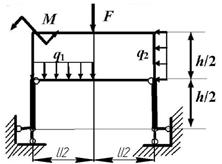
Задача 2. Расчет статически неопределимых рам методом сил

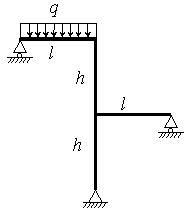
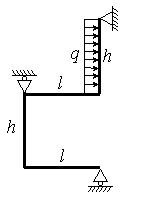
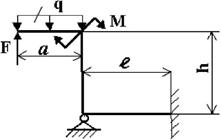
Для рамы (рис.2), соответствующей варианту задания, с размерами и нагрузкой, выбранными по шифру из табл.2, требуется методом сил построить эпюры М, Q и N.

Таблица 2

Номер cтроки	Номер схемы по рис.2	F1, кН	а, м	b, м	l, м	М, кНм	q, кН/м
01	1	12	1	2	2	24	5
02	2	10	2	2	3	16	4
03	3	12	3	2	4	12	6
04	4	6	2	3	2	18	2
05	5	8	1	3	5	20	4
06	6	10	3	1	6	12	2
07	7	6	2	2	3	12	3
08	8	8	1	2	2	12	6
09	9	6	2	1	4	16	5
10	10	12	1	3	3	10	6
11	11	11	1	2	5	12	6
12	12	12	3	3	1	18	2
13	13	10	2	3	2	20	4
14	14	12	1	1	4	12	2
15	15	6	2	2	5	12	3
16	16	8	1	2	3	12	6
17	17	10	2	1	2	18	5
18	18	6	3	2	5	20	6
19	19	8	2	2	3	12	2
20	20	6	1	3	2	12	4
21	21	12	3	3	1	12	2
22	22	12	2	1	3	16	3
23	23	13	1	2	4	10	6
24	24	14	1	2	5	12	5
25	25	12	3	1	3	18	6
26	26	10	2	3	2	20	6
27	27	12	1	2	1	12	2
28	28	6	2	3	3	24	4
29	29	8	1	3	5	16	2
30	30	10	2	1	4	12	3
31	31	6	3	2	2	18	6
32	32	8	2	2	1	20	5
33	33	6	1	1	3	12	6
34	34	12	3	3	6	12	2
35	35	11	2	2	4	16	4
36	36	8	1	2	3	20	3
	г	в	а	в	а	б	а

1 схема 2 схема 3 схема

4 схема 5 схема 6 схема

7 схема 8 схема 9 схема

10 схема 11 схема 12 схема

13 схема 14 схема 15 схема

16 схема 17 схема 18 схема

19 схема 20 схема 21 схема

22 схема 23 схема 24 схема

25 схема 26 схема 27 схема

28 схема 29 схема 30 схема

31 схема 32 схема 33 схема

34 схема 35 схема 36 схема

Рис.2

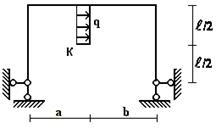
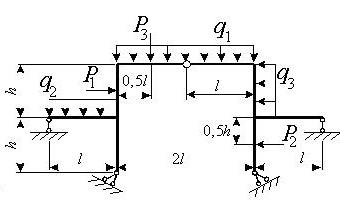
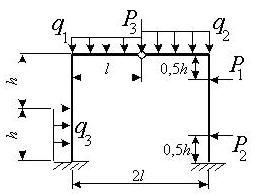
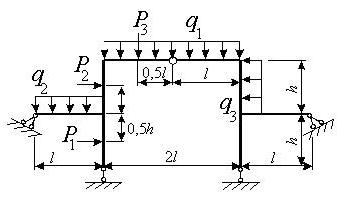
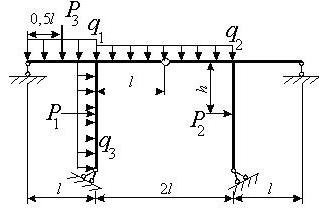
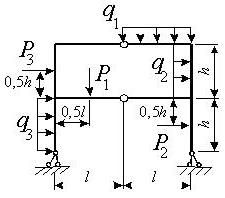
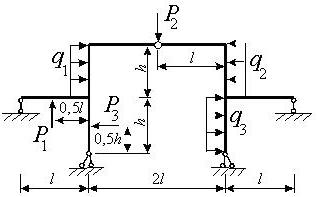
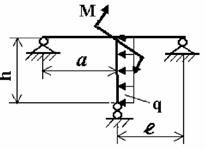
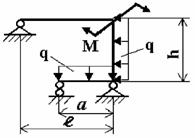
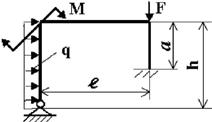
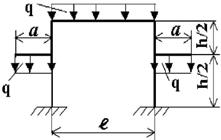
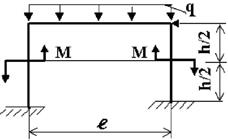
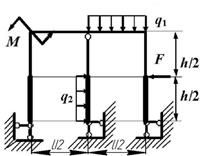
Задача 3. Расчет статически неопределимых рам методом сил

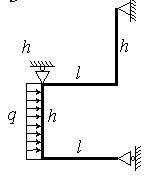
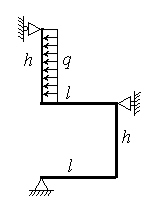
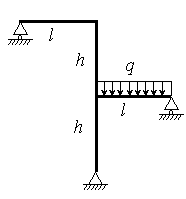
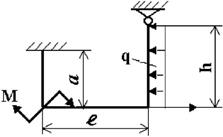
Для заданной статически неопределимой рамы (рис.3) с заданными в табл.3 размерами и нагрузками требуется построить эпюры изгибающих моментов, поперечных и продольных сил.

Таблица 3

Номер cтроки	Номер схемы по рис.3	l, м	h, м	P1, кН	P2, кН	P3, кН	q1, кН/м	q2, кН/м	q3, кН/м	I1/I2
1	1	10	6,0	4,0	0	0	1,8	0	0	0,5
2	2	17	5,5	0	4,5	0	0	1,9	0	2,0
3	3	19	5,0	0	0	5,0	0	0	2,0	0,3
4	4	12	9,5	3,6	0	0	2,2	0	0	3,0
5	5	11	9,0	0	2,0	0	0	2,1	0	0,7
6	6	13	8,5	0	0	3,2	0	0	2,3	1,5
7	7	14	8,0	8,0	0	0	1,7	0	0	0,6
8	8	15	6,5	0	6,0	0	0	2,4	0	1,7
9	9	16	7,0	0	0	3,0	0	0	2,5	0,8
10	10	18	7,5	2,0	0	0	1,6	0	0	1,3
11	11	17	5,3	0	2,8	0	0	1,6	0	0,4
12	12	19	6,7	0	0	3,7	0	0	2,2	1,8
13	13	10	5,6	2,2	0	0	1,5	0	0	0,9
14	14	11	7,3	0	3,3	0	0	1,7	0	1,0
15	15	15	5,9	0	0	3,9	0	0	2,3	1,2
16	16	12	7,6	2,4	0	0	1,9	0	0	1,4
17	17	11	6,1	0	3,4	0	0	1,8	0	1,6
18	18	16	7,9	0	0	4,2	0	0	2,4	1,9
19	19	13	6,4	2,6	0	0	2,0	0	0	2,5
20	20	14	8,1	0	3,5	0	0	2,1	0	2,2
21	1	19	6,7	0	0	3,7	0	0	2,2	1,8
22	2	10	5,6	2,2	0	0	1,5	0	0	0,9
23	3	11	7,3	0	3,3	0	0	1,7	0	1,0
24	4	15	5,9	0	0	3,9	0	0	2,3	1,2
25	5	12	7,6	2,4	0	0	1,9	0	0	1,4
26	6	11	6,1	0	3,4	0	0	1,8	0	1,6
27	7	16	7,9	0	0	4,2	0	0	2,4	1,9
28	8	13	6,4	2,6	0	0	2,0	0	0	2,5
29	9	14	8,1	0	3,5	0	0	2,1	0	2,2
30	10	19	5,0	0	0	5,0	0	0	2,0	0,3
31	11	12	9,5	3,6	0	0	2,2	0	0	3,0
32	12	11	9,0	0	2,0	0	0	2,1	0	0,7
33	13	13	8,5	0	0	3,2	0	0	2,3	1,5
34	14	14	8,0	8,0	0	0	1,7	0	0	0,6
35	15	15	6,5	0	6,0	0	0	2,4	0	1,7
36	16	16	7,0	0	0	3,0	0	0	2,5	0,8
	в	а	г	б	а	г	б	в	а	б

I₁ – момент инерции ригеля, I₂ – момент инерции стойки.

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

11 схема 12 схема

13 схема 14 схема

15 схема 16 схема

17 схема 18 схема

19 схема 20 схема

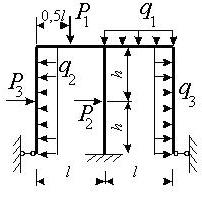
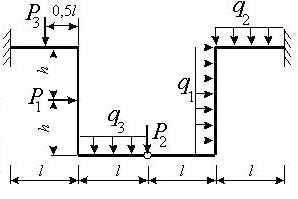
Рис.3

Пояснения к решению задачи

Для упрощения расчета рекомендуется принять симметричную основную систему. Можно применить и разложение нагрузки и неизвестных на симметричные и кососимметричные.

При построении единичных и грузовых эпюр изгибающих моментов необходимо приводить определение опорных реакций. Эпюры изгибающих моментов должны быть построены со стороны растянутых волокон. При "перемножении" эпюр следует пользоваться способом Верещагина.

После определения значений неизвестных рекомендуется построить эпюры моментов . Суммирование этих эпюр между собой и с грузовой эпюрой дает окончательную эпюру моментов. Суммирование рекомендуется производить по характерным точкам и в пояснениях обязательно приводить все расчеты.

Подсчет поперечной силы Q удобнее производить по формуле

где Q⁰ – "балочная" поперечная сила (найденная для данного участка как для простой балки на двух опорах); М_пр – момент на правом конце участка; М_лев – момент на левом конце участка; l – длина участка.

Эпюра N строится по эпюре поперечных сил путем вырезания узлов (как принято при расчете ферм), начиная с узла, в котором количество неизвестных продольных сил не превышает двух. При вырезании каждого узла учитывается, что положительная поперечная сила вращает узел по ходу часовой стрелки, а отрицательная – против.

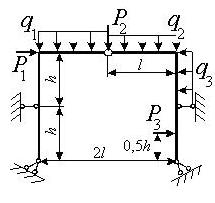
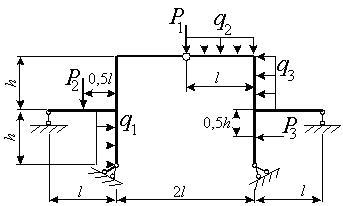
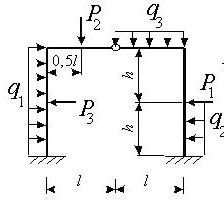
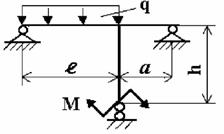
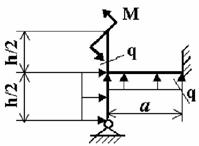
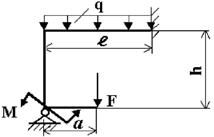
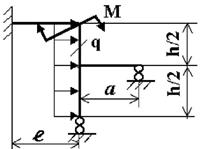
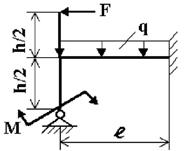
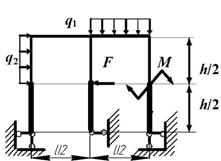
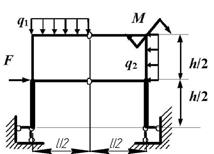
Задача 4. Расчет статически неопределимых рам методом сил

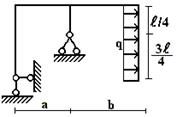
Для заданной статически неопределимой рамы (рис.4) с заданными в табл.4 нагрузками требуется определить опорные реакции.

Таблица 4

Номер cтроки	Схема по рис.4	P, кН	F, кН	q, кН/м
1	1	14	12	2
2	2	8	8	6
3	3	30	12	3
4	4	24	12	6
5	5	14	12	6
6	6	24	15	6
7	7	16	12	3
8	8	24	6	3
9	9	30	15	1
10	10	8	5	2
11	11	32	12	6
12	12	21	15	4
13	13	18	10	5
14	14	8	6	2
15	15	8	9	3
16	16	21	5	5
17	17	42	5	2
18	18	7	18	4
19	19	16	9	3
20	20	8	12	6
21	21	24	6	6
22	22	21	12	4
23	23	24	8	6
24	24	40	11	3
25	25	8	6	3
26	26	28	12	6
27	27	8	10	3
28	28	12	10	2
29	29	7	18	4
30	30	24	8	6
31	31	7	6	4
32	32	42	10	6
33	33	21	10	4
34	34	21	6	2
35	35	6	15	1
36	36	8	12	6
	б	а	в	г

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

11 схема 12 схема

13 схема 14 схема

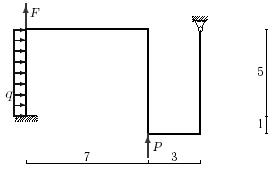
15 схема 16 схема

17 схема 18 схема

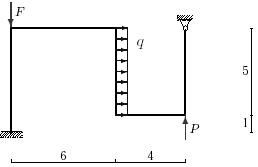
19 схема 20 схема

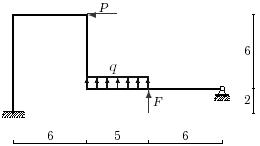
21 схема 22 схема

23 схема 24 схема

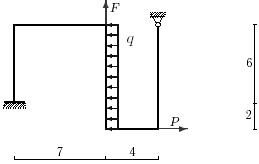
25 схема 26 схема

27 схема 28 схема

29 схема 30 схема

31 схема 32 схема

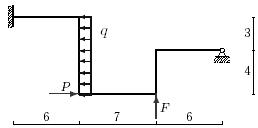
33 схема 34 схема

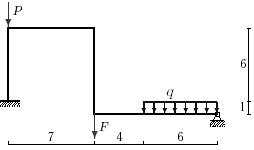
35 схема 36 схема

Рис.4

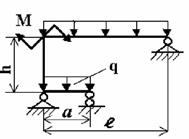
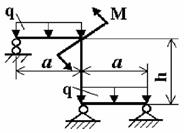
Задача 5. Расчет статически неопределимых рам методом сил

Для заданной статически неопределимой рамы при указанных размерах и нагрузках требуется:

1. Установить степень статической неопределимости.

2. Найти «лишние» опорные реакции с помощью канонических уравнений метода сил.

3. Построить эпюры продольных сил, поперечных сил и изгибающих моментов.

4. Выполнить проверку расчета.

Примечание: Данные для решения взять в табл. 5 и на рис. 5.

Таблица 5

Номер строки	Схема по рис.5	Параметры	Числовые значения вариантов
01	1	М, кНм	20	30	10	15	20	15	25	40	10	20
02	2	F, кН	25	15	60	45	15	10	10	20	35	20
03	3	q, кН/м	10	12	14	16	18	20	30	24	20	28
04	4	h, м	2,5	3,5	3,0	2,5	3,0	2,0	2,5	3,0	3,0	2,5
05	5	L, м	2,0	4,0	2,0	3,0	4,0	2,5	2,0	1,0	2,5	3,0
06	6	A, м	1,0	1,7	1,5	1,0	1,5	1,5	1,0	1,5	1,5	1,5
07	7	М, кНм	30	45	25	30	25	24	35	20	35	20
08	8	F, кН	45	30	35	50	65	20	50	35	25	20
09	9	q, кН/м	10	15	15	18	20	30	20	25	27	20
10	10	H, м	2,5	3,0	2,0	2,0	2,5	2,5	3,0	3,0	3,0	3,0
11	11	L, м	3,0	2,0	3,0	4,0	4,5	2,5	3,0	2,0	3,5	4,0
12	12	A, м	1,8	1,0	1,5	1,6	1,0	1,2	1,5	1,0	2,0	1,8
13	13	М, кНм	30	40	20	20	40	26	25	60	30	20
14	14	F, кН	24	25	35	65	30	30	30	50	65	35
15	15	q, кН/м	30	30	30	10	10	35	20	35	15	10
16	16	H, м	3,0	3,0	2,5	3,0	2,5	3,0	2,5	2,0	3,0	2,5
17	17	L, м	4,0	4,0	2,0	2,5	3,0	4,0	3,0	3,0	2,0	4,0
18	18	А, м	2,0	1,5	1,0	1,5	1,4	2,0	1,4	1,0	1,5	2,0
19	19	М, кНм	30	45	25	30	25	24	35	20	35	20
20	20	F, кН	45	30	35	50	65	20	50	35	25	20
21	21	q, кН/м	10	15	15	18	20	30	20	25	27	20
22	22	H, м	2,5	3,0	2,0	2,0	2,5	2,5	3,0	3,0	3,0	3,0
23	23	L, м	3,0	2,0	3,0	4,0	4,5	2,5	3,0	2,0	3,5	4,0
24	24	A, м	1,8	1,0	1,5	1,6	1,0	1,2	1,5	1,0	2,0	1,8
25	25	М, кНм	30	45	25	30	25	24	35	20	35	20
26	26	F, кН	45	30	35	50	65	20	50	35	25	20
27	27	q, кН/м	10	15	15	18	20	30	20	25	27	20
28	28	H, м	2,5	3,0	2,0	2,0	2,5	2,5	3,0	3,0	3,0	3,0
29	29	L, м	3,0	2,0	3,0	4,0	4,5	2,5	3,0	2,0	3,5	4,0
30	30	A, м	1,8	1,0	1,5	1,6	1,0	1,2	1,5	1,0	2,0	1,8
	а		б	в	г	а	б	в	г	а	б	в

1 схема 2 схема

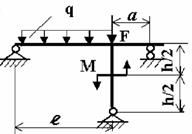
3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

11 схема 12 схема

13 схема 14 схема

15 схема 16 схема

17 схема 18 схема

19 схема 20 схема

21 схема 22 схема

23 схема 24 схема

25 схема 26 схема

27 схема 28 схема

29 схема 30 схема

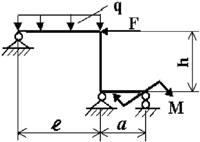
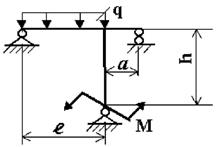
Рис. 5

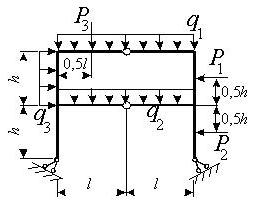
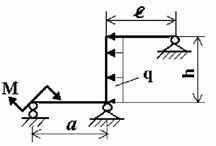
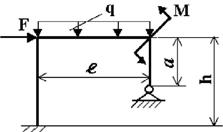
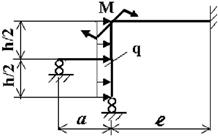
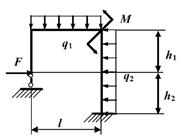
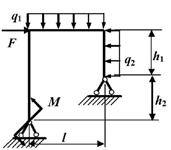
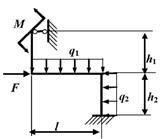
Задача 6. Расчет статически неопределимых рам

Исходные данные к задачам принимаются по табл. 6 и схемам на рис. 6.

1. Нарисуйте схему конструкции рамы в масштабе. Отрицательные нагрузки направьте в сторону, противоположную показанной на рисунке. Покажите на рисунке размеры рамы и величины нагрузок в численном виде.

2. Найдите степень статической неопределимости заданной системы.

3. Выберите основную систему, отбросив лишние связи, и приложите к основной системе лишние неизвестные (реакции в отброшенных связях).

4. Запишите условие совместности деформаций и раскройте его, определив деформации любым способом.

5. Из условия совместности деформаций найдите значение лишней неизвестной.

6. Постройте окончательные эпюры внутренних усилий.

7. Изобразите на рисунке изогнутую ось рамы.

8. Выполните проверку, перемножив окончательную эпюру изгибающих моментов и эпюру моментов от единичной силы.

9*. Исследуйте, как изменится эпюра изгибающих моментов, если одну шарнирно подвижную опору сделать упругой (в виде пружины). Коэффициент жесткости пружины считайте заданной величиной.

Таблица 6

Номер строки	Схема по рис. 6	h2, м	l, м	F, кН	M, кНм	q1, кН/м	q2, кН/м	h1, м
01	10	1	3	20	0	10	0	1
02	9	2	4	0	40	0	10	2
03	8	3	5	-10	0	-20	0	3
04	7	4	6	0	-50	0	-20	1
05	6	2	5	10	0	30	0	2
06	5	1	4	0	-60	0	30	3
07	4	3	3	-20	0	20	0	1
08	3	4	4	0	-40	0	20	2
09	2	5	5	-30	0	0	-10	3
10	1	3	6	0	20	-10	0	2
	б	г	в	а	б	г	в	а

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

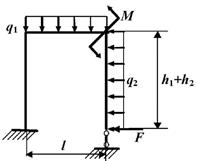
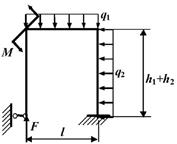
7 схема 8 схема

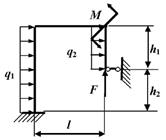
9 схема 10 схема

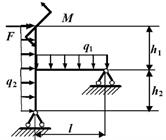
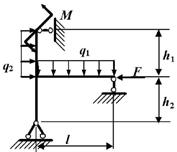
Рис. 6

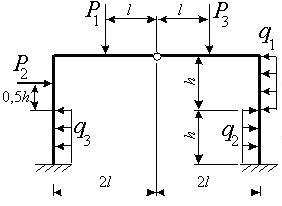
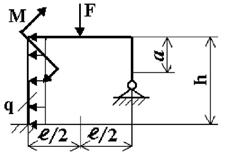
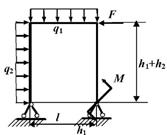
Задача 7. Расчет статически неопределимой рамы с шарнирами с учетом симметрии

Исходные данные к задаче принимаются по табл. 7 и схемам на рис. 7.

1. Нарисуйте схему рамы в масштабе. Отрицательные нагрузки направьте в сторону, противоположную показанной на рисунке.

2. Определите степень статической неопределимости рамы.

3. Выберите основную систему, сохраняя симметрию конструкции. Приложите к основной системе лишние неизвестные.

4. Запишите систему канонических уравнений метода сил для определения лишних неизвестных и найдите коэффициенты этой системы уравнений. Для этого выполните следующее:

- разложите заданную нагрузку, включая лишние неизвестные (если это необходимо) на симметричную и кососимметричную части;

- постройте эпюры изгибающих моментов:

а) от симметричной части нагрузки;

б) от кососимметричной части нагрузки;

в) от единичных значений лишних неизвестных (или от симметричной или кососимметричной частей лишних неизвестных);

- перемножьте соответствующие эпюры моментов по правилу Верещагина (Симпсона) для определения коэффициентов системы канонических уравнений.

5. Решите систему уравнений и найдите значения лишних неизвестных.

6. Постройте окончательные эпюры внутренних усилий N, Q, M и сделайте проверку, перемножив окончательную эпюру M на эпюры моментов от единичных сил.

Таблица 7

Номер строки	Схема по рис. 7	l, м	h, м	q1, кН/м	q2, кН/м	F, кН	M, кНм	I2/I1
01	1	4	6	20	0	20	0	2
02	2	6	8	0	-20	0	-60	2,5
03	3	8	6	30	0	30	0	3
04	4	6	4	0	-30	0	-50	1,5
05	5	8	10	40	0	40	0	2
06	6	6	8	0	-40	0	60	2,5
07	7	4	6	-40	0	-50	0	3
08	8	6	10	0	20	0	40	1,5
09	9	10	8	-20	0	-60	0	2
10	10	8	6	0	40	0	20	2,5
	в	г	а	б	в	г	а	б

Примечание. I₂/I₁ – отношение моментов инерции нижней и верхней частей стоек.

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

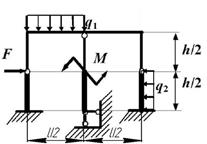
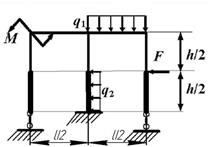
Рис. 7

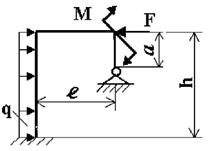
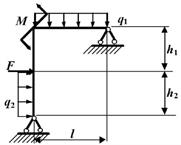
Задача 8. Расчет статически неопределимой рамы

Для статически неопределимой рамы (рис.8) требуется:

1) раскрыть статическую неопределимость,

2) построить эпюры внутренних силовых факторов,

3) выполнить деформационную проверку.

Расчет выполнить в буквенном виде, выражая N_z и Q_y через Р, а М_х через Рl.

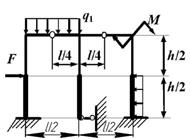
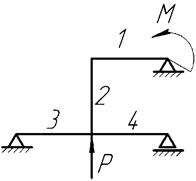
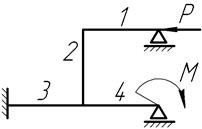
Принять длины стержней 1, 2, 3, 4 равными l. M=2Pl.

1 схема 2 схема 3 схема

4 схема 5 схема 6 схема

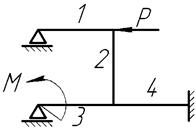
7 схема 8 схема 9 схема

10 схема 11 схема 12 схема

13 схема 14 схема 15 схема

16 схема 17 схема 18 схема

19 схема 20 схема 21 схема

22 схема 23 схема 24 схема

Рис.8

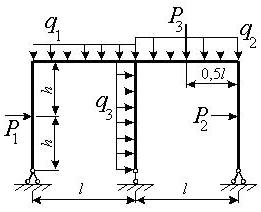
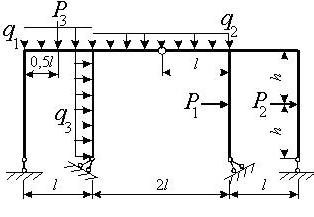
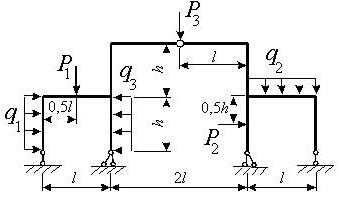
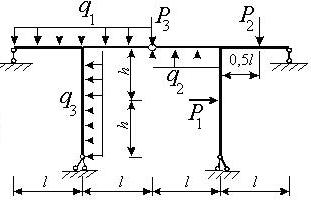
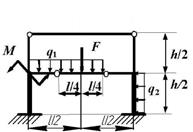
Задача 9. Расчет статически неопределимой рамы

Для расчета заданной статически неопределимой рамы (рис.9) требуется:

1) раскрыть статическую неопределимость методом сил и построить эпюры М, Q, N;

2) произвести проверку правильности построения эпюр;

3) провести ее расчет на ЭВМ.

Исходные данные определяются по табл. 9. и рис.9.

Таблица 9

Номер cтроки	Номер схемы по рис.9	l, м	h, м	P1, кН	P2, кН	q1, кН/м	q2, кН/м	I1/I2
1	1	6	8	6	0	2	0	2:1
2	2	9	4	9	0	3	0	3:1
3	3	12	4	0	8	0	3	3:2
4	4	6	8	0	8	0	2	4:1
5	5	10	4	10	0	5	0	5:3
6	6	8	6	8	0	2	0	2:1
7	7	6	6	0	6	0	3	3:1
8	8	9	8	0	8	0	3	3:2
9	9	12	6	12	0	4	0	4:1
10	10	6	4	6	0	2	0	2:3
11	11	6	8	6	0	2	0	2:1
12	12	9	4	9	0	3	0	3:1
13	13	12	4	0	8	0	3	3:2
14	14	6	8	0	8	0	2	4:1
15	15	10	4	10	0	5	0	5:3
16	16	8	6	8	0	2	0	2:1
17	17	6	6	0	6	0	3	3:1
18	18	9	8	0	8	0	3	3:2
19	19	12	6	12	0	4	0	4:1
20	20	6	4	6	0	2	0	2:3
21	21	6	8	6	0	2	0	2:1
22	22	9	4	9	0	3	0	3:1
23	23	12	4	0	8	0	3	3:2
24	24	6	8	0	8	0	2	4:1
25	25	10	4	10	0	5	0	5:3
26	26	8	6	8	0	2	0	2:1
27	27	6	6	0	6	0	3	3:1
28	28	9	8	0	8	0	3	3:2
29	29	12	6	12	0	4	0	4:1
30	30	6	4	6	0	2	0	2:3
31	1	6	8	6	0	2	0	2:1
32	2	9	4	9	0	3	0	3:1
33	3	12	4	0	8	0	3	3:2
34	4	6	8	0	8	0	2	4:1
35	5	10	4	10	0	5	0	5:3
36	6	8	6	8	0	2	0	2:1
	а	б	г	в	г	б	а	б

I₁ – момент инерции горизонтальных и наклонных стержней, I₂ – момент инерции вертикальных стержней.

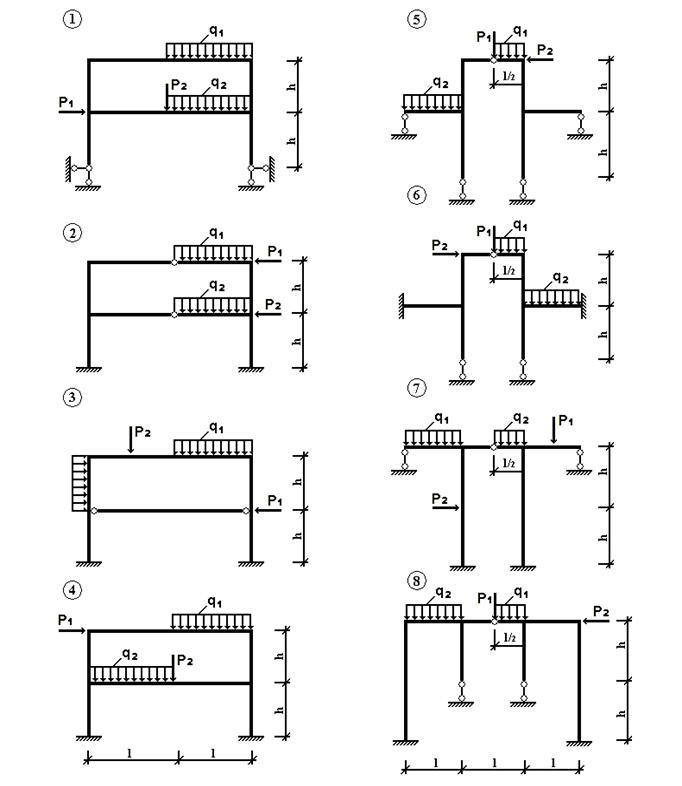
Рис.9

Пояснения к решению задачи

Расчет статически неопределимой рамы может быть произведен различными методами. Одним из распространенных является метод сил. За основные (лишние) неизвестные силы в данном случае принимаются реактивные силы в отброшенных связях системы. Расчет рамы начинается с нахождения степени ее статической неопределимости, которая может быть установлена по формуле

Л= 3К – Ш. (1)

При кинематическом анализе заданной статически неопределимой системы можно выделить необходимые связи и «лишние» связи. Необходимые связи – связи, отбрасывание которых приводит к геометрической или мгновенной изменяемости основной системы. Лишние связи – связи, отбрасывание которых не приводит к геометрической или мгновенной изменяемости системы.

Вычислив количество лишних связей, приступают к выбору основной системы и назначению неизвестных. Основной явится та статически определимая система, которая получена из заданной статически неопределимой после устранения лишних связей. Желательно получить наиболее простую основную систему. Если заданная система симметричная, то основная система должна быть симметричной. Наиболее удачным ее выбор считается тогда, когда большинство побочных перемещений обратятся в нули.

Действие отброшенных связей заменяется неизвестными усилиями. Основная система должна быть: 1) статически определимой и 2) геометрически неизменяемой.

Количество возможных основных систем неограниченно. Для простых задач выбор той или иной основной системы диктуется, как правило, простотой построения в них единичных и грузовой эпюр, что приводит к уменьшению трудоемкости расчета. При образовании основной системы могут быть использованы следующие приемы (показаны на примере системы, изображенной на рис. 9(1), а):

- устранение опорных связей (рис. 9(1), б);

- введение шарниров (рис. 9(1), в);

- рассечение элементов (рис. 9(1), г);

- сочетание приемов (рис. 9(1), д).

На рис. 9(1), е, ж показаны примеры неудачного выбора основной системы.

Для симметричных рам (рис. 9(1), а) эффективна группировка неизвестных (рис. 9(1), з, и), приводящая к заметному сокращению количества счета.

Рис. 9(1). Выбор основной системы

После этого составляются канонические уравнения. В общем случае они запишутся в следующем виде:

δ₁₁∙x₁+ δ₁₂∙x₂+ δ₁₃∙x₃+…+ δ_1n∙x_n+∆_1p=0;

δ₂₁∙x₁+ δ₂₂∙x₂+ δ₂₃∙x₃+…+ δ_2n∙x_n+∆_2p=0; (2)

………………………………………..

δ_n1∙x₁+ δ_n2∙x₂+ δ_n3∙x₃+…+ δ_nn∙x_n+∆_np=0.

Физический смысл уравнений состоит в том, что перемещение по направлению каждой неизвестной сил от всех неизвестных сил и от заданной нагрузки должно равняться нулю, так как в заданной системе имеются связи по направлению неизвестных сил.

Каждый коэффициент при неизвестном, входящем в каноническое уравнение (δ₁₁, δ_12, δ_nn), есть перемещение основной системы по направлению неизвестных от единичных сил . Например, δ₁₂ перемещение по направлению силы от действия единичной силы . Свободные члены уравнения (Δ_1p, Δ_2p, Δ_np) представляют собой перемещения основной системы по направлению неизвестных от заданной нагрузки.

Коэффициенты при неизвестных и свободные члены канонических уравнений определяются с помощью интеграла Мора по формулам

Если в раме стержни прямолинейны и по длине имеют одинаковую жесткость, то можно определить коэффициенты при неизвестных и свободные члены по правилу А.Н.Верещагина (перемножением эпюр) по выражениям

где ω – площадь одной из эпюр изгибающих моментов; – ордината другой (обязательно прямолинейной) эпюры, взятой по центру тяжести эпюры ω. Важно отметить, что ордината должна быть вычислена обязательно из прямолинейной эпюры.

Площадь эпюр и место положения ординаты центра тяжести можно определить с помощью готовых таблиц. Коэффициенты δ_nn всегда положительны, коэффициенты δ_in и свободные члены ∆_np могут быть как положительными, так и отрицательными, а также равными нулю. Для определения коэффициентов при неизвестных и свободных членов уравнения необходимо построить «единичные» эпюры изгибающих моментов. Другими словами, нужно построить эпюры изгибающих моментов: – от силы x₁=1; – от силы x₂=1 и т. д. Кроме того, можно построить эпюру М_р от действия на основную систему заданных нагрузок.

После определения коэффициентов при неизвестных и свободных членов уравнения необходимо выполнить проверку правильности их вычисления, для чего надо построить также суммарную единичную эпюру

(5)

и вычислить δ_ss; сумма δ_ik вычисляется отдельно. Если они определены правильно, то должно удовлетворяться следующее условие

Свободные члены проверяются условием

(7)

Если не выполняется универсальная проверка (6), то для отыскания ошибки следует провести построчные проверки:

……………………………………………

Определив коэффициенты при неизвестных и свободные члены канонических уравнений и выполнив все проверки, приступают к решению системы канонических уравнений, из которой определяют значения неизвестных x₁, x₂, x₃, …, x_n. Затем полученные значения неизвестных необходимо поставить в исходные уравнения, для того чтобы убедиться в правильности выполненного решения.

После определения неизвестных можно приступить к построению окончательной эпюры изгибающих моментов M. Это может быть осуществлено с помощью одного из следующих приемов.

Прием первый. Ординаты эпюр от единичных воздействий умножить соответственно на числовые значения найденных неизвестных x₁, x₂, x₃, …, x_n с учетом знаков (т.е. построить эпюры ). Построить эпюру М путем сложения соответствующих ординат эпюр с эпюрой изгибающих моментов от внешней нагрузки M_p.

Прием второй. Приложить к основной системе заданные нагрузки, найденные усилия x₁, x₂, x₃, …, x_n (с учетом знака) и построить эпюру М как для обычной статически определимой системы.

Окончательная эпюра изгибающих моментов должна быть обязательно проверена с помощью следующего условия:

Это может быть проделано путем умножения эпюры М (по правилу А.Н.Верещагина) на суммарную единичную эпюру . Результат должен быть равным нулю или близким к нему:

Проведенная проверка называется кинематической. Кроме этого необходимо еще выполнить и статическую проверку, т.е. должно быть выполнено условие равновесия для каждого узла ΣM=0.

Ординаты эпюры изгибающих моментов откладываются в стороны растянутого волокна. Эпюра поперечных сил строится с помощью эпюры изгибающих моментов. Если последняя прямолинейна, то поперечная сила определяется по выражению

На участках, где данная эпюра криволинейная, эпюра поперечных сил вычисляется по формуле

где Q^б – «балочная» поперечная сила, которая рассчитывается для данного сечения как для простой балки на двух шарнирных опорах; M_пр – момент на правом конце рассматриваемого участка (положительный, если он действует против хода часовой стрелки); M_лев – момент на левом конце рассматриваемого участка (положительный, если он действует по ходу часовой стрелки); l – длина рассматриваемого стержня.

Поперечная сила считается положительной, если для совмещения оси элемента с касательной к эпюре изгибающих моментов приходится вращать эту ось по ходу часовой стрелки; вращение должно производиться так, чтобы угол поворота был не больше 90º.

Для определения направления поперечной силы надо провести через данное сечение элемента разрез и к каждой его части приложить поперечную силу. Если она положительная, то должна вращать каждую часть элемента по ходу часовой стрелки.

Эпюра продольных сил N строится с помощью эпюры поперечных сил путем вырезания узлов, как это делается при расчете статически определимых ферм, начиная с узла, в котором количество неизвестных продольных сил не более двух. Зная поперечные силы в узлах и внешнюю нагрузку, продольные силы находим из условия равновесия суммы проекций на выбранные оси координат:

ΣX=0 или ΣY=0. (13)

Для проверки полученных эпюр Q и N нужно провести сечение и отделить от рамы какую-либо часть, в местах сечения положить продольные и поперечные силы и внешнюю нагрузку. Если эпюры построены правильно, то будут удовлетворены условия равновесия действующих усилий отсеченной части рамы:

ΣX=0; ΣY=0.

Примеры расчета рам методом сил

Пример 1.

Для заданной статически неопределимой рамы (рис. 10) требуется:

а) раскрыть статическую неопределимость методом сил и построить эпюры М, Q и N;

б) произвести проверку правильности построения эпюр;

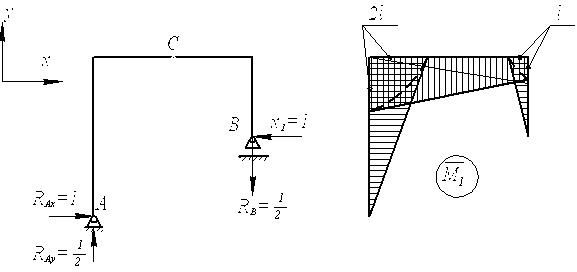
Рис.10

Решение.

1. Определяется степень статической неопределимости системы: Л = 3К – Ш =3·2 – 2=4.

2. Выбирается основная система. Рама симметричная, следовательно, основную систему следует выбирать также симметричной (рис. 11).

Рис.11

3. Записываются канонические уравнения методом сил. Их будет столько, сколько лишних связей:

δ₁₁∙x₁+ δ₁₂∙x₂+ δ₁₃∙x₃+δ₁₄∙x₄+∆_1p=0;

δ₂₁∙x₁+ δ₂₂∙x₂+ δ₂₃∙x₃+δ₂₄∙x₄+∆_2p=0;

δ₃₁∙x₁+ δ₃₂∙x₂+ δ₃₃∙x₃+δ₃₄∙x₄+∆_3p=0;

δ₄₁∙x₁+ δ₄₂∙x₂+ δ₄₃∙x₃+δ₄₄∙x₄+∆_4p=0.

4. Определяются перемещения, входящие в канонические уравнения. Для этого строятся эпюры изгибающих моментов от единичных сил и внешней нагрузки: (рис. 12)

Рис.12

5. Вычисляются коэффициенты и свободные члены канонических уравнений с помощью построенных единичных и грузовых эпюр.

Для этого используется правило А.Н.Верещагина и формула трапеций:

а) находятся значения коэффициентов и свободных членов канонических уравнений:

Аналогично определяются

б) выполняется проверка полученных результатов. Для этого строится суммарная единичная эпюра:

(рис. 12);

Проверка показала, что полученные значения коэффициентов при неизвестных и свободных членов уравнений найдены правильно.

6. Найденные значения коэффициентов при неизвестных и свободных членов подставляются в канонические уравнения и сокращаются на .

Получается следующая система:

10,314∙x₁ + 0∙x₂ + 16,726∙x₃ + 0,314∙x₄ + (-754,354) =0

0∙x₁ + 336∙x₂ + 0∙x₃ + 0∙x₄ + 2910 =0;

16,726∙x₁ + 0∙x₂ + 105,362∙x₃ + 6,058∙x₄ + 6120,36 =0

0,314∙x₁ + 0∙x₂ + 6,058∙x₃ + 7,646∙x₄ + 605,046 =0.

7. Полученную систему канонических уравнений можно решить любым способом: сокращенным алгоритмом Гаусса, способом итерации на ЭВМ.

В результате решения получены следующие значения неизвестных:

x₁=224,104; x₃=-92,81;

x₂=-8,661; x₄=-14,798.

Для проверки правильности решения все неизвестные подставляются в систему канонических уравнений:

10,314∙224,104 + (-92,814)∙16,726 + 0,314∙(-14,798) - 754,354=0;

0∙224,104 + 336∙(-8,661) + 0∙(92,814) + 0∙(-14,796) + 2910=0;

16,726∙224,104 + 105,362∙(-92,814) + 6,058∙(-14,798) + 6120,36=0;

0,314∙224,104 + 6,058∙(-92,814) + 7,646∙(-14,798) + 605,046=0.

8. Строится окончательная эпюра изгибающих моментов (рис. 13):

Рис.13

9. Проводится кинематическая и статическая проверки правильности построения окончательной эпюры изгибающих моментов:

а) кинематическая проверка заключается в соблюдении условия

б) статическая проверка заключается в проверке равновесия всех узлов рамы (рис. 14).

Рис.14

10. По построенной эпюре изгибающих моментов строится эпюра поперечных сил:

а) для стержней, загруженных внешней нагрузкой, поперечная сила определяется по формуле

б) для стержней, не загруженных внешней нагрузкой, поперечная сила определяется по формуле

По полученным результатам строится эпюра поперечных сил (рис. 15).

Рис.15

11. По эпюре поперечных сил строится эпюра продольных сил (рис. 16).

Рис.16

12. Выполняется статическая проверка правильности построения эпюр поперечных и продольных сил. Для этого отбрасываются опорные связи и их действие заменяется силами, взятыми с эпюр Q и N . Система под действием всех сил должна находиться в равновесии (рис. 17).

ΣX=0; ΣY=0;

ΣX= (139,573 - 145,081)∙0,8321 + (2,885 + 5,436)∙0,5547 = -4,613 + 4,615 = 0,002.

Погрешность

ΣY= -100 - 10 + (-2,885 + 5,436)∙0,8321 + (139,537 – 145,081)∙0,5547 = 2160 +160,004 = 0,004.

Погрешность

Рис.17

Пример 2.

Для рамы, изображенной на рис.18, а, требуется построить эпюры изгибающих моментов, поперечных и продольных сил.

Решение.

1. Кинематический анализ

По формуле определяем число лишних связей n (степень статической неопределимости) заданной стержневой системы:

n= 2Ш+С₀-3Д=2∙2+7-3∙3=2.

Здесь: Ш=2 – шарниры B, C; C₀=7 – опорные связи по три в заделках D, E и одна связь в шарнирно подвижной опоре A, Д=3 – диски ABD, BC, CE; (рис. 18, а).

2. Выбор основной системы

На рис. 18, б и рис. 19, а представлены два варианта основной системы, удовлетворяющие требованиям статической определимости и геометрической неизменяемости. На рис. 19, б приведен пример неудачного выбора основной системы: для диска ABD оставлена одна лишняя связь (например, опора А), в то время как для дисков BC, CE удалена необходимая связь (например, вертикальная), что превращает эту часть сооружения в механизм с одной степенью свободы.

Рис. 18. Расчет рамы методом сил

Рис. 19. Выбор основной системы метода сил

Будем работать с основной системой, представленной на рис. 18, а. В стержне ВС возникает только продольная сила. Разрежем этот стержень: на рис. 18, б концы стержня в месте разреза (точки b, c) условно разнесены один от другого. Неизвестную продольную силу обозначим x₁.

Отбросим опору в точке А и ее действие на раму заменим усилием x₂. Таким образом, x₂ – это опорная реакция в точке А.

3. Формирование системы канонических уравнений метода сил

Для нашей задачи система канонических уравнений имеет вид:

Здесь:

– сближение точек b и c, вызванное силами ;

– сближение точек b и c от действительного значения силы ;

– сближение точек b и c, вызванное силой ;

– сближение точек b и c от действительного значения силы ;

– сближение точек b и c от заданной нагрузки.

– вертикальное перемещение точки А, вызванное силами );

– вертикальное перемещение точки А от действительного значения силы ;

– вертикальное перемещение точки А, вызванное силой ;

– вертикальное перемещение точки А от действительного значения силы ;

– вертикальное перемещение точки А от заданной нагрузки.

Смысл первого уравнения состоит в запрещении сближения/удаления точек b и c, смысл второго уравнения – в запрещении вертикального перемещения точки А. Именно при этих условиях основная система (рис. 18, б) будет работать эквивалентно заданной (рис. 18, а).

3.1. Построение единичных эпюр изгибающих моментов

Единичные эпюры моментов и строятся в основной системе от и соответственно (рис. 18, в, г). Суммарная единичная эпюра от сил и , действующих одновременно, показана на рис. 18, д. Поскольку эпюра равна сумме эпюр и , то можно переходить к следующему пункту задачи.

На рис. 18, в, г, д ординаты эпюр в начале участков выделены более крупным шрифтом в сравнении с ординатами в середине участков.

3.2. Определение коэффициентов системы канонических уравнений

Коэффициенты системы уравнений подсчитываем по формуле

3.3. Проверка коэффициентов канонических уравнений

Поскольку , то переходим к следующему пункту задачи.

3.4. Построение грузовой эпюры изгибающих моментов

Грузовая эпюра моментов строится в основной системе от заданной нагрузки (рис.18, е) – ординаты эпюры в начале участков выделены более крупным шрифтом в сравнение с ординатами в середине участков.

3.5. Определение свободных членов системы канонических уравнений

Свободные члены подсчитываем по формуле

3.6. Проверка свободных членов канонических уравнений

Поскольку , то переходим к следующему пункту задачи.

4. Решение системы канонических уравнений

Система канонических уравнений с учетом подсчитанных значений коэффициентов приобретает вид

Решаем полученную систему уравнений. Для этого умножим второе уравнение на -315/324:

и сложим первое уравнение с измененным вторым. В результате получим

Откуда и

5. Построение окончательных (расчетных) эпюр изгибающих моментов, поперечных и продольных сил

5.1. Построение расчетной эпюры моментов

Строим исправленные эпюры , (рис. 18, ж, з). Расчетная эпюра моментов (рис. 18, и) получается сложением грузовой эпюры (рис. 18, е) с единичными исправленными: . Сложение эпюр осуществляется поточечно.

Например, для вертикального участка от точки D до точки приложения силы имеем: в точке D M_н = 10,942 - 73,900 + 50= -12,958; в сечении под силой M_к= 3,647 - 73,900 + 80 = 9,747. Соединяем эти две ординаты прямой линией. Для горизонтального участка от точки А до точки приложения силы имеем: в точке А M_н = 0; в точке под силой M_к= 0 + 36,950 – 16 = 20,950; посередине участка M_c= 0 + 18,475 - 4=14,475. По этим трем точкам строим квадратную параболу. Для других участков вычисления аналогичны.

5.2. Кинематическая проверка

Поскольку

5.3. Построение расчетной эпюры поперечных сил

Поперечную силу на участке определяем по формуле

Участок от опоры А до точки приложения силы:

Участок от точки приложения силы до точки В:

Участок СЕ:

Вертикальный участок от точки В до точки приложения силы:

Вертикальный участок от точки приложения силы до точки D:

По данным проведенного расчета построена расчетная эпюра поперечных сил (рис. 18, к).

5.4. Построение расчетной эпюры продольных сил

В нашем случае определение продольных сил следует начать либо с узла А, либо с узла С, и продолжить рассмотрением узла В.

Начнем с узла С.

Из уравнения равновесия ΣF_x=0: -N_BС – 1,216 =0 находим N_BС= -1,216 кН.

Из уравнения равновесия ΣF_y=0 находим N_CE=0.

Узел В:

ΣF_x=0: -N_AB – 1,216 + 1,216=0; N_AB=0;

ΣF_y=0: -N_BD – 10,762 = 0; N_BD= -10,762 кН;

По данным проведенного расчета построена расчетная эпюра продольных сил (рис. 18, л).

5.5. Статическая проверка

В заданной системе (рис. 18, а) отбрасываем опоры. Их действие на раму заменяем усилиями согласно построенным эпюрам M, Q, N (рис. 18, м). Проверяем выполнение уравнений равновесия

ΣF_y=0: 9,238 + 10,762 – 4 - 2∙8 = 20 – 20 = 0,

ΣF_x=0: 5 - 3,784 - 1,216 = 5 – 5 = 0,

ΣM₀=0: 2∙8∙4 + 4∙4 + 5∙6 - 10,762∙8 – 12,958 – 1,216∙3 - 7,295 = 110 – 109,997 = -0,03 ≈ 0 [(110-109,997)/109,997∙100=0,003<1%]

Выполнение кинематической и статической проверок подтверждает правильность построения эпюр M, Q, N.

Пример 3.

Для рамы, изображенной на рис.20, требуется построить эпюры изгибающих моментов, поперечных и продольных сил. Жесткости стержней приняты постоянными, равными EJ. Размерности сил и моментов – кН и кНм, распределенной нагрузки – кН/м, линейные размеры – м.

Рис.20

Решение.

1. Кинематический анализ

Степень статической неопределимости данной рамы (см. рис. 20) равна с=3∙к-ш,

где к – число замкнутых контуров; ш – число одиночных шарниров: шарнир, соединяющий два стержня, считается одиночным, три стержня – двойным и т.д.

Степень статической неопределимости с=3∙2-4=2, так как замкнутые контуры представлены шарнирно-неподвижной опорой A и контуром ACDB, а число одиночных шарниров равно 4.

2. Выбор основной системы

Основная система может быть образована отбрасыванием связей в шарнирно-неподвижной опоре A. На рис.21 представлена основная система, загруженная внешними силами. X₁ и X₂ – реакции в отброшенных «лишних» связях, направленные, как правило, по горизонтали и вертикали.

Рис. 21

3. Построение эпюр изгибающих моментов в основной системе от действия внешней нагрузки и единичных сил

На рис. 22, а, б построены единичные эпюры моментов.

а) б)

Рис. 22

Грузовые эпюры строят в основной системе.

На рис. 23 построены грузовые эпюры моментов при действии заданной нагрузки (в соответствии с рис. 21) в размерности кНм.

Рис. 23

4. Канонические уравнения метода сил

Канонические уравнения метода сил для дважды статически неопределимой рамы имеют вид

δ₁₁∙X₁+δ₁₂∙X₂+∆_1F=0;

δ₂₁∙X₁+δ₂₂∙X₂+∆_2F=0, (1)

где δ_ij – единичные перемещения, первый индекс i показывает направление, второй индекс j – причину (например, δ₁₂ – перемещение по направлению от силы ); ∆_if – грузовые перемещения.

5. Вычисление единичных перемещений

5.1. Определение δ_ii

δ_ii определяются перемножением единичных эпюр самих на себя по правилу Верещагина (см. рис.22, а, б):

где – площадь единичной эпюры изгибающих моментов на i- м участке; – ордината, взятая на эпюре под центром тяжести.

5.2. Определение 𝛿_ij (i≠j)

δ_ij определяются по формуле Мора с использованием правила Верещагина – взаимного перемножения единичных эпюр (см. рис. 22, а, б):

где – площадь участка единичной эпюры (см. рис. 22, а); – ордината, взятая на эпюре (см. рис. 22, б) под центром тяжести площади участка эпюры . Суммирование производится по участкам. Коэффициенты побочной диагонали равны

6. Универсальная проверка единичных перемещений

Определим сумму единичных перемещений (с учетом знаков), равную δ_Si=δ₁₁+δ₁₂+δ₂₁+δ₂₂=314,66/EJ.

Сложив, учитывая знаки, соответствующие ординате эпюр и (см. рис. 22, а, б), получим суммарную единичную эпюру .

Данная операция необходима для проверки правильности вычисления единичных перемещений. Она заключается в равенстве суммы единичных перемещений и суммарных единичных перемещений δ_Si=Σδ_i,j.

Рис. 24

Для этого перемножим эпюру саму на себя по правилу Верещагина (рис. 24).

Следовательно, коэффициенты определены правильно.

7. Определение грузовых перемещений

Грузовые перемещения определяют путем перемножения эпюр M_F на и соответственно (см. рис. 22, а, б и рис. 23).

8. Универсальная проверка грузовых перемещений

Перемножим эпюру (см. рис. 23) на эпюру (см. рис. 24)

где ω_iF – площадь участка грузовой эпюры M_F; – ордината эпюры под центром тяжести участка эпюры M_F. Вычисления дают по участкам.

Оценка правильности определения грузовых перемещений производится по условию: алгебраическая сумма грузовых перемещений должна быть равна сумме грузовых перемещений по направлениям 1 и 2. Таким образом, перемещение ∆_sF под действием внешних сил в направлениях 1 и 2 равно

Суммирование по участкам

Погрешность не превышает 0,01%.

9. Решение системы канонических уравнений

Запишем систему алгебраических уравнений согласно формуле (1), сократив на 1/EJ:

432X₁-366X₂-1622=0; (2)

-366X₁+554X₂+20160=0.

а) б)

Рис. 25

Решение системы (2) дает X₁==-46,468 кН; X₂=-64,572 кН.

Перемножая ординаты эпюр и на X₁, X₂ (с учетом их знаков), получим эпюры и Данные эпюры приведены на рис. 25.

10. Построение окончательной эпюры изгибающих моментов

Окончательную эпюру моментов в заданной системе получим просуммировав эпюры (см. рис. 23), и (см. рис. 25, а, б). .

Эпюра M_F показана на рис. 26.

Примечание. Эпюры изгибающих моментов должны быть построены на сжатых волокнах. Сложение ординат эпюр проводят с учетом знака. Знак определяется расположением эпюры относительно стержня на данном участке. Например, знак минус – эпюра на внутренней стороне контура, следовательно знак плюс – эпюра на внешней стороне контура.

Рис. 26

11. Деформационная проверка окончательной эпюры изгибающих моментов

Задача, решаемая при деформационной проверке, – получение равенства нулю перемещений по выбранным ранее направлениям приложенных сил X₁ и X₂. Необходимо окончательную эпюру M_F умножить на любую единичную или суммарную единичную:

Погрешность составляет

12. Построение эпюр поперечных и продольных сил в статически неопределимой системе

Дифференцированием окончательной эпюры M_F вычисляем значения эпюр поперечных сил Q. Эпюру Q вычисляем по формуле

где Q⁰ – поперечная сила в сечении простой балки от заданной нагрузки; M_пр и M_лев – опорные моменты на левом и правом концах участка; d – длина участка. Например, для участка AC (рис. 26, а) Q⁰ = 20 кН, т.к. горизонтальная нагрузка, равная F=40 кН, приложена в середине. Момент M=158,808 кНм взят с окончательной эпюры M_F (см. рис. 26). Тогда с учетом знака Q⁰

а) б) в)

Рис. 27

На рис.27, б – эпюра поперечных сил от нагрузки F=40.

На рис.27, в – эпюра момента на участке AC от M_F в узле C.

На рис.28 показана эпюра поперечных сил в размерности кН.

Рис. 28

Примечание. Положительные значения эпюры Q откладываются на внешних сторонах стержней рамы при условии расположения наблюдателя внутри рассматриваемого контура. Для данной рамы контуры обозначены буквами: первый контур – A, B, C, D; второй контур – B, D, E, K.

Продольные силы в стержнях определяют из условия равновесия узлов.

Главный вектор сил в узле равен нулю при отсутствии внешней силы в узле. При наличии сосредоточенной силы в узле условие равновесия имеет вид . В соответствии с этим построим эпюру продольных сил N. На рис. 29, а, б, в даны расчетные схемы узлов C, E, D.

а) б) в)

Рис. 29

Узел C (рис. 29, а). Сумма проекций сил на горизонтальную ось X-N_CE=Q_CA =6,468 кН.

Сумма проекций сил на вертикальную ось Y-N_CA=Q_CE =64,572 кН.

Узел E (рис. 29, б). ΣY=0; N_ED=Q_EK=100 кН.

Узел D (рис. 29, в). ΣY=0; N_DB=Q_DC+N_DE=64,572+100=164,572 кН.

На рис. 30 приведена эпюра продольных сил в размерности кН.

Рис. 30

Примечание. Рассмотрим равновесие узла C (см. рис. 29, а). В узел входят стержни AC и CE. Согласно эпюре Q с учетом правила знаков для поперечных сил укажем направления их. Q_CA=6,468 направлена по часовой стрелке вокруг узла: (знак (+)); Q_CE=-64,572 – против часовой стрелки (знак (-)). Следовательно, при проецировании сил на горизонтальную ось продольная сила N_CE=6,468 стержня CE должна быть растягивающей. Сила N_CA=64,572 получена из условия равновесия при проецировании на вертикальную ось. Остальные узлы рассмотрены аналогично узлу С.

13. Статическая проверка

Сумма проекций всех сил (внешних и реакций связей) на любую ось равна нулю.

Сумма моментов всех сил (внешних и реакций связей) относительно любой точки рамы равна нулю.

На рис. 31 дана схема статически определимой рамы с указанием сил и моментов.

Рис. 31

Сумма проекций сил на вертикальную ось:

ΣY=-R_A+R_B-F=64,572+164,572-100=0.

Сумма проекций сил на горизонтальную ось:

ΣX=-H_A+F+H_B=-46,468+40+6,468=0.

Уравнение моментов вокруг точки B:

Σm_B=0; Q∙5+F∙3-R_A∙8-M_B=100∙5+40∙3-64,572∙8-103,424=0.

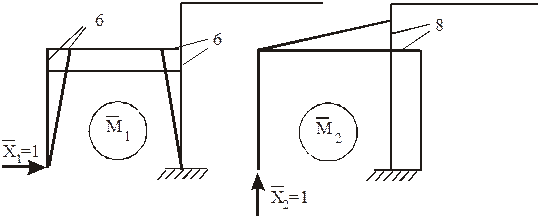
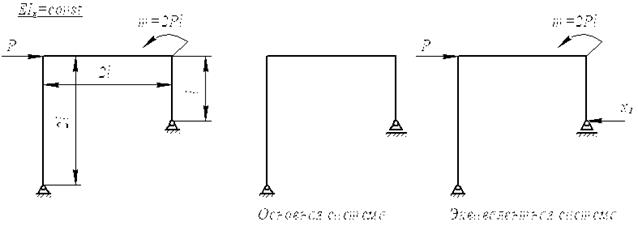
Пример 4.

Раскрыть статическую неопределимость рамы (рис.32, а) и построить эпюры внутренних силовых факторов.

а) б) в)

Рис.32

1. Выбираем основную систему (рис.32, б).

2. Рисуем эквивалентную систему (рис.32, в).

3. Каноническое уравнение метода сил δ₁₁X₁+∆_1p=0.

а) б)

Рис.33. Единичное нагружение

Определяем реакции опор в единичном нагружении (рис. 33, а):

2) Из уравнения ΣY=0 следует

3) Из уравнения ΣX=0 следует

Проверка:

Далее строим эпюру . (рис.33, б).

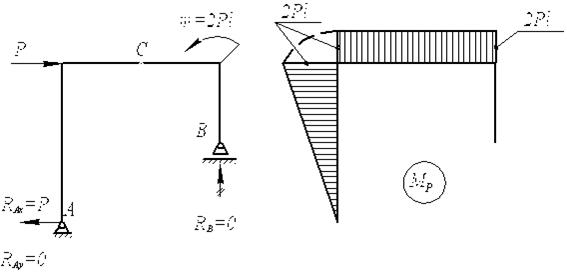
Рис.34. Грузовое нагружение

Определяем реакции в грузовом нагружении (рис. 34):

2) Из уравнения ΣY=0 следует

3) Из уравнения ΣX=0 следует

Проверка:

Строим эпюру моментов М_Р. Умножаем эпюру на (рис. 33).

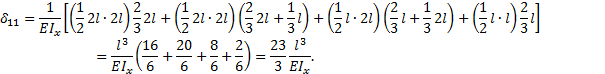
Умножаем эпюру М_Р на (рис. 34 и 33).

Решаем каноническое уравнение

Вычисляем реакции (рис. 35) и строим эпюры N_z, Q_y и М_х (рис. 36).

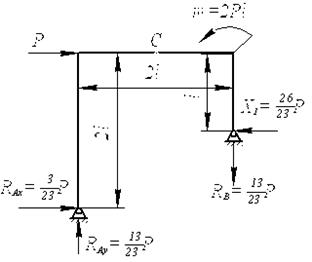
Рис.35. Схема рамы с найденными реакциями

Проверка:

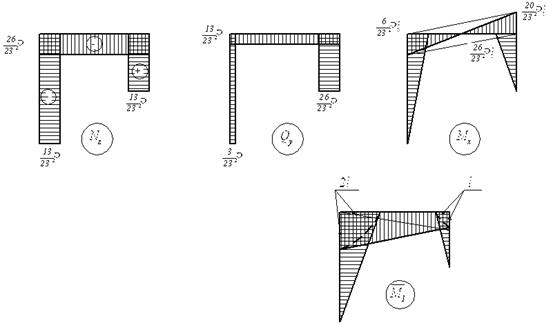
Рис.36. Окончательные эпюры

Деформационная проверка:

Умножаем эпюру М_х на .

Пример 5.

Рассмотрим в качестве объекта расчета статически неопределимую раму (рис. 37).

Рис. 37

Решение.

Сформулируем последовательность шагов, которые следует выполнить при решении задачи:

1. Определение степени статической неопределимости: n=5-3=2.

2. Выбор основной системы. Основной называется статически определимая, геометрически неизменяемая система, незагруженная внешними силами и “лишними” неизвестными. Варианты основных систем, которые можно получить из заданной системы (рис. 37), приведены на рис. 38.

В первом варианте (рис. 38,а) в качестве “лишних” неизвестных были приняты горизонтальная и вертикальная реакции на правой опоре. Во втором варианте (рис.38,б) в качестве “лишних” неизвестных были приняты реакция в горизонтальной связи на правой опоре и опорный момент на левой опоре. При создании третьего варианта основной системы был врезан простой шарнир в тело рамы. Это понизило степень статической неопределимости на единицу. Для снижения степени статической неопределимости еще на единицу на левой опоре был врезан еще один шарнир. В качестве “лишних” неизвестных в третьем варианте были приняты опорный момент на левой опоре и внутренний момент, действующий в узле, соединяющем стойку и ригель балки.

Рис.38. Варианты основных систем

3. Построение эквивалентной системы путем нагружения основной системы внешними силами и “лишними” неизвестными. Выбирая в качестве основной системы вариант (рис.38,а), изобразим эквивалентную систему (рис.39).

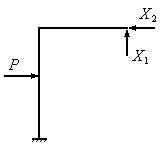
Рис.39. Эквивалентная система

Действие отброшенных связей в этой системе заменяется неизвестными силами X₁ и X₂. Изображенная на рис.39 система будет эквивалентной заданной системе лишь в том случае, если перемещения в месте отброшенных связей по их направлению будут равны нулю (условия эквивалентности):

∆₁(P, X₁, X₂)=0, (1)

∆₂(P, X₁, X₂)=0, (2)

Уравнения (1), (2) удобно записывать в канонической (упорядоченной) форме:

δ₁₁X₁ + δ₁₂X₂ + ∆_1P = 0; (3)

δ₂₁X₁ + δ₂₂X₂ + ∆_2P = 0. (4)

Геометрический смысл уравнения (3) состоит в равенстве нулю перемещений в направлении первой “лишней” неизвестной силы X₁, вызванных самой силой X₁ (δ₁₁X₁), силой X₂ (δ₁₂X₂) и внешней нагрузкой (∆_1P). Геометрический смысл уравнения (4) состоит в равенстве нулю перемещений в направлении второй “лишней” неизвестной силой X₂, вызванных самой силой X₂ (δ₂₂X₂), силой X₁ (δ₂₁X₁) и внешней нагрузкой (∆_2P).

Канонические уравнения составляются в соответствии с определенным правилом независимо от степени статической неопределимости системы и от реального геометрического смысла каждого из уравнений. Для n раз статически неопределимой задачи система канонических уравнений принимает вид:

где i-е уравнение канонической системы уравнений метода сил приравнивает к нулю перемещение в i-м сечении эквивалентной системы под действием заданных внешних сил и всех “лишних” неизвестных.

4. Вычисление свободных членов и коэффициентов канонической системы уравнений.

Свободные члены (грузовые члены) системы канонических уравнений () выражают перемещения сечений в месте отброшенных связей, вызванных внешними силами. Геометрический вид этих перемещений для рамы, изображенной на рис.39, приведен на рис.40,а.

Для определения этих перемещений следует построить грузовую эпюру изгибающих моментов (рис.40,б), единичные эпюры (рис.40,г,е) и перемножить соответствующим образом грузовую и единичные эпюры, пользуясь формулой Мора:

В практических случаях для вычисления этих перемещений удобно пользоваться формулой Мора-Симпсона

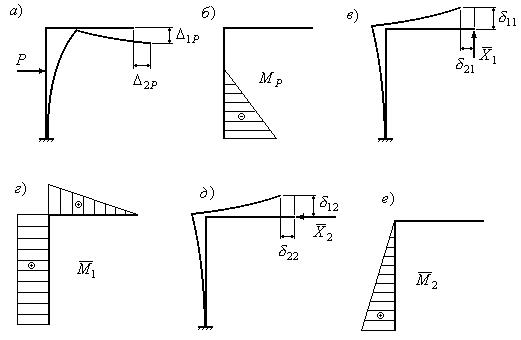
Рис. 40

Коэффициенты системы канонических уравнений (единичные члены) выражают перемещение сечения системы, вызванное действием единичной силы. Например, коэффициент δ_ij представляет собой перемещение i-го сечения основной системы от приложения единичной силы в сечении j. Определяются единичные коэффициенты из формулы Мора:

В практических случаях для определения единичных коэффициентов системы канонических уравнений метода сил удобно пользоваться формулой треугольников

Единичные коэффициенты могут быть главными, если оба индекса у них одинаковы δ_ii. Главные коэффициенты всегда больше нуля. Эти коэффициенты стоят на главной диагонали системы канонических уравнений. Побочные коэффициенты δ_ij могут быть положительными, отрицательными или равными нулю. Из теоремы Максвелла следует правило взаимности этих коэффициентов:

δ_ij=δ_ji. (8)

Правило взаимности коэффициентов позволяет существенно сократить число вычислений по определению единичных коэффициентов системы канонических уравнений метода сил.

5. Решение системы канонических уравнений относительно “лишних” неизвестных. В результате мы получаем ряд “лишних” неизвестных X₁, X₂, ….., X_n, которые используются для определения суммарных изгибающих моментов.

6. Определение величин суммарных изгибающих моментов с помощью выражения . Этот способ определения изгибающих основан на принципе независимости действия сил. Суммарные изгибающие моменты определяются путем алгебраического сложения эпюр изгибающих моментов от внешней нагрузки и от “лишних” неизвестных. Вид суммарной эпюры изгибающих моментов для рамы (рис.37) приведен на рис.41.

Рис.41. Суммарная эпюра изгибающих моментов

7. Проверка правильности построения суммарной эпюры изгибающих моментов.

а) Статическая проверка. Проверяется выполнение равновесия узлов по моментам. Вырезается узел, в котором сходятся несколько стержней, действие отброшенных частей рамы заменяется моментами и составляется уравнение равновесия, представляющее равенство нулю моментов в узле: ΣM=0. У рассматриваемой рамы всего один такой узел (рис.42).

Рис.42

б) Деформационная проверка. Для выполнения этой проверки выбираем дополнительную основную систему, например, для рассматриваемой рамы такой дополнительной основной системой может быть система, изображенная на рис.38,б. Здесь в качестве “лишней” неизвестной принят опорный момент на левой опоре. Обозначим его X₃. Нагрузим дополнительную основную систему единичным моментом и построим эпюру единичных моментов . Умножим суммарную эпюру изгибающих моментов на эпюру , используя формулу Мора (6), в которой изгибающий момент M_P заменяется изгибающим моментом M_S. В равной степени для определения перемещений при выполнении деформационной проверки можно использовать формулу Мора-Симпсона (6.1). Полученное произведение должно тождественно равняться нулю. С точки зрения физического смысла это означает, что угол поворота сечения на левой опоре равен нулю. В практических задачах при округлении получаемых чисел в процессе расчета конструкции накапливаются ошибки. Поэтому в большинстве случаев тождественное равенство искомых перемещений отсутствует. В связи с этим принято в уравнении перемещений при выполнении деформационной проверки отдельно суммировать положительные члены (А), отдельно отрицательные (В) и относительную погрешность определять по формуле:

Эта погрешность не должна превышать 3%. В этом случае можно считать, что деформационная проверка сходится.

8. Построение эпюры суммарной эпюры поперечных сил Q_S.

Эпюра Q_S строится методом вырезания участков. Предположим, что мы хотим построить эпюру поперечных сил на участке рамы 1-2 (рис.43).

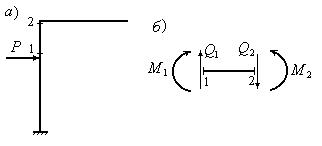
Рис.43

С этой целью мы вырезаем участок 1-2 (рис.43,а) и прикладываем в сечениях №1 и №2 поперечные силы (рис.43,б). Поскольку их величины и знак неизвестны, прикладываем их такими, чтобы они были положительными в соответствии с правилом знаков для поперечной силы. Кроме поперечных сил в сечениях №1 и №2 прикладываем моменты, действующие в этих сечениях . Эти моменты берем из суммарной эпюры изгибающих моментов. Составляя суммы моментов относительно сечений №1 и №2, находим соответственно значения поперечной силы Q₂ и Q₁. Следует отметить, что при наличии распределенной нагрузки ее нужно прикладывать к вырезанному участку и учитывать ее влияние на величину поперечных сил. Определив таким образом величину поперечной силы во всех “характерных” сечениях, строим эпюру поперечных сил. Для контроля правильности построения эпюры поперечных сил следует пользоваться следствиями из дифференциальных зависимостей между поперечной силой и изгибающим моментом.

Возможный вид эпюры поперечных сил приведен на рис.44.

Рис.44. Суммарная эпюра поперечных сил

9. Построения эпюры продольных сил.

Продольные усилия в стержнях рамы определяются методом вырезания узлов. Вырежем узел рамы (рис.45). Приложим к узлу продольные силы N₂, N₃ и поперечные силы Q₂ и Q₃, взятые из суммарной эпюры поперечных сил Q_S.

Рис.45

Суммируя силы, действующие в узле на оси x и y, найдем продольные силы N₂ и N₃. Суммарная эпюра продольных усилий N_S приведена на рис.46.

Рис.46. Суммарная эпюра продольных сил

Пример 6.

Для статически неопределимой рамы (рис. 47) построить эпюры М, Q, N и проверить решение.

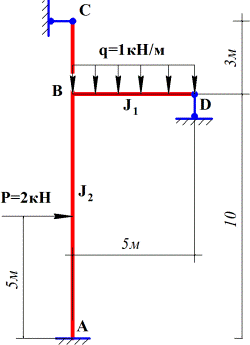
Рис. 47

Решение.

1. Определим степень статической неопределимости по формуле:

Л = С₀ + 2Ш – 3Д;

где: С₀ – число опорных связей; С₀ = 4;

Ш – число простых промежуточных шарниров, Ш = 0;

Д – число жестких дисков, Д = 1.

Л = 5+2·0-3·1 = 2.

Рама два раза статически неопределима.

2. Выбираем основную систему, удалив одну, горизонтальную опорную связь, взамен этой удаленной связи приложим неизвестное усилие Х₁ (рис. 48)

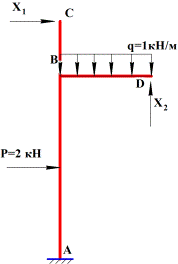
Рис. 48

3. Составим систему канонических уравнений метода сил:

где: δ₁₁ – перемещение точки по направлению Х₁.

4. Построим эпюры изгибающих моментов в единичных и грузовой систем основной системы.

Х₁ = 1 (рис.49)

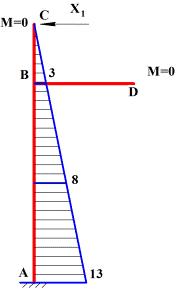
Рис. 49

Х₂ = 1 (рис.50)

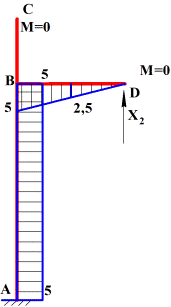
Рис. 50

В грузовом состоянии (рис.51 и 52).

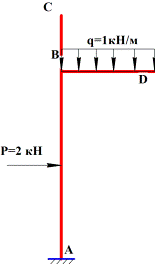
Рис. 51

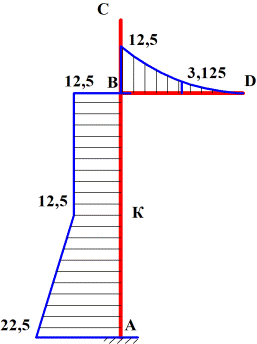
Рис. 52

4. Коэффициенты уравнения определяются по формуле Мора. Если жесткость стержня EY по длине постоянна, формула Мора имеет такой вид:

где М₁ и М_р – соответственно эпюры моментов в единичном и грузовом состоянии основной системы. Интеграл Мора можно вычислить по формуле Симпсона:

Где L – длина перемножаемого участка стержня;

M – численные значения ординат эпюр моментов.

После построить эпюры моментов в единичном и грузовом состоянии для основной системы.

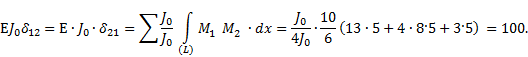
5. Решим систему канонических уравнений по алгоритму Гаусса.

№ уравнений	№ строк	Х1	Х2	D1P	проверка
I	1	183,1	100,00	-320,83	0,21
	2	-1	-0,546	1,75	0,21
II	1	100	104,17	-265,63	20,62
	2	100	-54,62	175,24	20,62
II’	1	0	49,5	90,39	0,82
	2	0	-1	1,82	0,82

II’ = -Х₂ + (1,82) = 0

Х₂ =1,82.

I = -Х₁ + (-0,546)∙(1,82) + 1,75= 0;

Х₁ = 0,756.

6. Построим окончательные эпюры изгибающих моментов (рис.53). Умножаем ординаты единичных эпюр на найденные значения перемещений Z₁ и Z₂; вычисляем ординаты грузовой эпюры в основной системе.

М_Х = М₁∙Х₁ + М₂∙Х₂ +М_Р;

M_АВ = 13∙ (0,756)+ 5∙ (1,82)- 22,5= -3,55 кНм.

М_ВА = 3∙ (0,756)+ 5∙ (1,82)-12,5= -1,11кНм.

М_ВС = 3∙0,756 =2,27 кНм.

М_К = 8∙0,756 +5∙1,82 - 12,5=2,67 кНм.

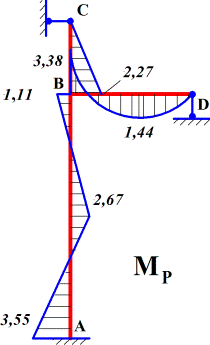
Рис. 53. Окончательная эпюра изгибающих моментов

7. Построим эпюры поперечных сил Q (рис.54).

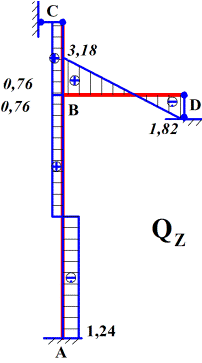
Рис. 54. Эпюра Q

8. Построим эпюры продольных сил N (рис.55).

Рис. 55. Эпюра N

9. Статическая проверка узлов (рис.56).

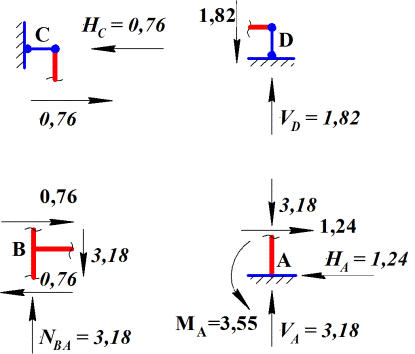
Рис. 56. Статическая проверка

10. Проверяем решение из условия равновесия рамы в целом.

К раме прикладываются заданные нагрузки и вычисленные опорные реакции (рис.57). Полученная произвольная плоская система сил должна удовлетворять всем уравнениям статики.

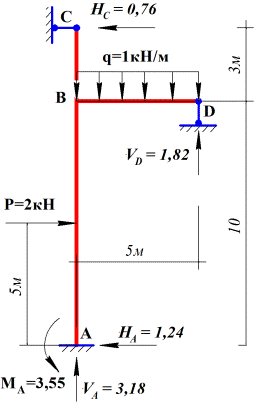
Рис. 57

Пример 7.

На рисунке 58 изображена плоская рама с двумя шарнирно неподвижными и одной шарнирно подвижной опорой.

Построить эпюры поперечной силы, изгибающего момента и продольной силы и определить перемещения.

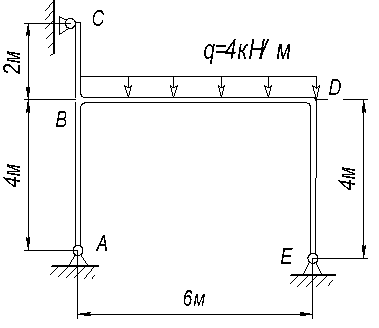
Рис. 58

Решение.

Количество наложенных связей 2+2+1=5.

Кинематическая неизменяемость плоской системы достигается наложением на нее трех связей. Столько же можно составить для нее независимых уравнений равновесия. Значит изображенная рама является дважды статически неопределимой. Составленные три уравнения равновесия не позволят определить 5 неизвестных реакций связей.

Если удалить "лишние" связи и к полученной раме, которая называется основной системой, приложить заданную нагрузку и силы, равные реакциям удаленных связей, то получим статически определимую систему, эквивалентную заданной. То есть деформация ее и внутренние силовые факторы такие же, как и у заданной конструкции. Значит перемещения ∆₁ и ∆₂ вдоль удаленных связей равны нулю.

На основании принципа независимости действия сил

∆₁=∆₁₁+∆₁₂+∆_1P=0;

∆₂=∆₂₁+∆₂₂+∆_2P=0. (1)

Здесь ∆_1k - перемещение вдоль i-ой удаленной связи от реакции X_k.

∆_1p - перемещение в этом же направлении от заданной нагрузки.

Перемещение ∆_1k можно представить произведением δ_ikX_k, в котором δ_ik - перемещение вдоль i-ой удаленной связи, но не от силы X_k, а от единичной силы, приложенной вместо X_k. Система уравнений (1) принимает вид

δ₁₁X₁+δ₁₂X₂+∆_1P=0;

δ₂₁X₁+δ₂₂X₂+∆_2P=0. (2)

Перемещение ∆_ip и δ_ik можно найти по методу Мора-Верещагина. Найденные реакции удаленных связей X₁ и X₂ позволяют построить эпюры внутренних силовых факторов для эквивалентной системы. Поскольку эквивалентная система испытывает такие же деформации, что и заданная, то внутренние силовые факторы, определенные для нее по найденным силам X_k, являются таковыми и для заданной системы.

На рис.59 приведены 4 конструкции, полученные удалением двух связей. Заметим, что вторая конструкция может иметь вертикальные поступательные перемещения без сопротивления приложенной нагрузке. Третья конструкция может поворачиваться вокруг оси опоры А на небольшой угол. При этом угол поворота рамы зависит от приложенных сил нелинейно. Значит вторая и третья рамы не могут быть приняты за основную систему.

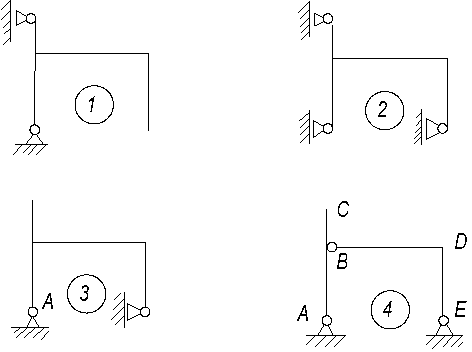
Рис. 59

Выберем в качестве основной системы последнюю раму. Она получена удалением опоры С, налагающей одну связь, и введением шарнира В, который допускает взаимный поворот сечений вертикальной балки АС и рамы BDE, примыкающих к узлу В. То есть удалены одна внешняя связь и одна внутренняя.

На рис.60 изображена эквивалентная система, к которой кроме заданной нагрузки приложена сила X₁, равная реакции опоры С и момент X₂ (обобщенная сила), равный изгибающему моменту в сечении В рамы BDE.

Рис. 60

Для вычисления коэффициентов δ_ik уравнений (2) построены эпюры изгибающих моментов и от единичных нагрузок (рис. 61).

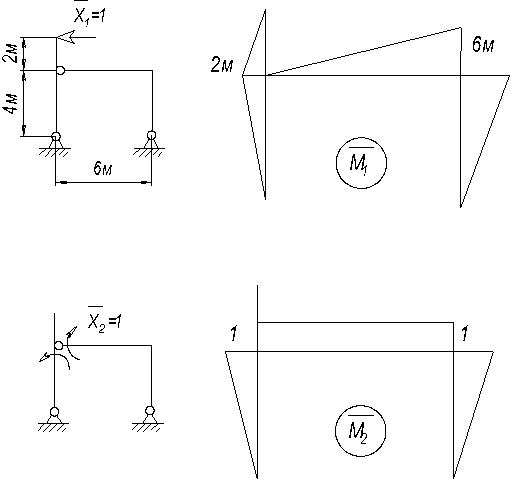
Рис. 61

Для вычисления перемещений ∆_ip построена грузовая эпюра (рис. 62)

Рис. 62

При вычислении перемещения δ₁₁ (или δ₂₂) единичная эпюра (или ) выступает в роли грузовой и в роли вспомогательной. Так что следует представить, что есть две эпюры (или ) и одна из них умножается на другую, такую же.

Канонические уравнения (2) принимают вид

После упрощения получаем

192X₁ + 43X₂ = -324;

43X₁ + 13X₂ = -108.

Решение уравнений:

X₁ = 0,668 кН; X₂ = -10,52 кН.

На рис. 63 изображена эквивалентная система при найденных значениях X₁ и X₂. Для определения реакций опор эквивалентной системы и построения эпюр внутренних силовых факторов рассмотрим равновесие балки АВС и рамы BDE в отдельности (рис. 64).

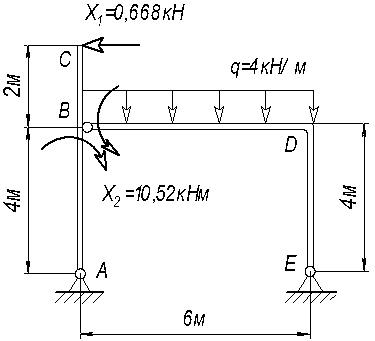
Рис. 63

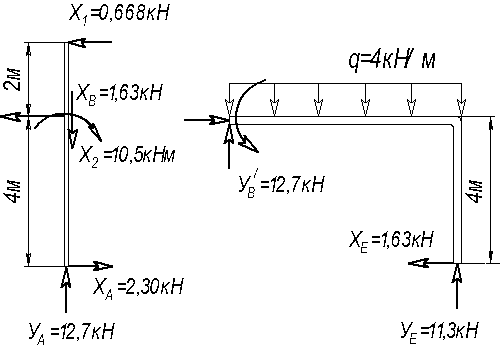
Рис. 64

По уравнению моментов относительно оси шарнира А найдем силу X_B.

0,668∙6 – 10,52 + X_B∙4 =0. X_B = 1,63 кН.

По уравнению моментов относительно шарнира В найдем силу X_A.

X_A∙4 + 0,668∙2 – 10,52 = 0. X_A = 2,30 кН.

X_B - это сила, с которой рама BDE действует на балку АВС. Значит

По уравнению моментов для рамы относительно шарнира Е найдем .

10,52 – 1,63∙4 +4∙6∙3 - ∙6 = 0. =12,67 кН.

По уравнению проекций сил на ось Х

X_E = X_B = 1,63 кН.

По уравнению проекций сил на ось y

12,67 - 4∙6 + Y_E = 0. Y_E = 11,33 кН.

Эпюры поперечной силы Q_y, изгибающего момента M_x и продольной силы N_z можно построить, не определяя сил взаимодействия балки АВС и рамы ВDЕ. Но реакции опор А и Е найти нужно.

На рис. 65 изображена неразделенная система сил.

Сила X_A находится по уравнению моментов сил, приложенных к балке АВС, относительно шарнира В.

X_A∙4 + 0,668∙2 – 10,52 = 0. X_A=2,30 кН.

По уравнениям моментов сил, приложенных ко всей раме, относительно шарниров А и Е находятся силы Y_E и Y_A.

Σm_A = 0. Y_E∙6 + 0,668∙6 - 4∙6∙3 = 0. Y_E = 11,3 кН.

Σm_E = 0. -Y_A∙6 + 0,668∙6 + 4∙6∙3 = 0. Y_A = 12,7 кН.

По уравнению проекций сил на ось x находится сила X_E

2,30 – 0,668 – X_E = 0. X_E = 1,63 кН.

На рисунках 66, 67, 68 изображены эпюры поперечной силы, изгибающего момента и продольной силы.

По построенной эпюре изгибающего момента можно определить перемещения сечений заданной рамы. Для этого необходимо иметь единичную эпюру. Но для построения единичной эпюры для заданной статически неопределимой рамы нужно опять, используя метод сил, удалить "лишние" связи, построить эквивалентную систему и повторить все последующие операции.

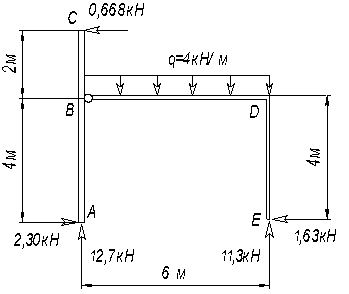
Рис. 65

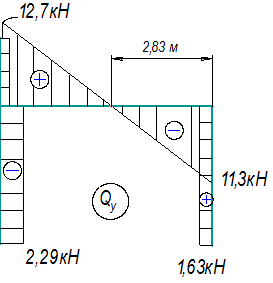
Рис. 66

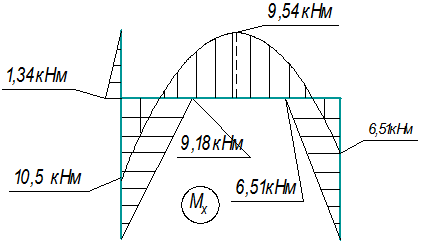
Рис. 67

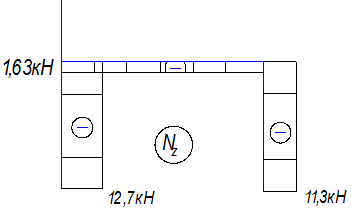
Рис. 68

Но можно обойти эти процедуры, если заметить, что построенная эпюра M_x является эпюрой изгибающего момента, как для эквивалентной системы, так и для заданной статически неопределимой, и что эти системы имеют одинаковые деформации и перемещения. Значит, определение перемещений заданной статически неопределимой рамы можно заменить определением перемещений эквивалентной ей статически определимой рамы, причем любой эквивалентной рамы, построенной на основании заданной. То есть единичная эпюра может быть построена для любой основной системы.

Например, найдем горизонтальное перемещение сечения В, используя ту же основную систему.

На рис. 69 изображена рама, нагруженная горизонтальной единичной силой и соответствующая ей эпюра изгибающего момента. По грузовой эпюре (рис. 70) и единичной эпюре (рис. 69) найдем горизонтальное перемещение сечения В.

Рис. 69

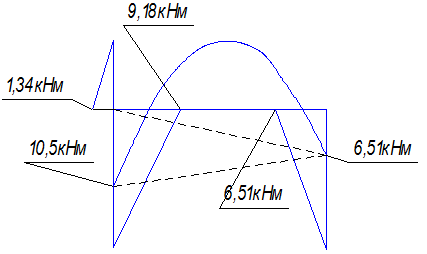
Рис. 70

Если в качестве вспомогательной выбрать раму, изображенную на рисунке 71, то единичная эпюра и перемножение эпюр окажется более простым.

Рис. 71

Результат тот же.

Рама, изображенная на рисунке 71, может быть использована для деформационной проверки эпюры, изображенной на рисунке 70. Для этого найдем, например, вертикальное перемещение сечения Е.

На рисунке 72 изображена соответствующая нагрузка и эпюра изгибающего момента .

Рис. 72

Перемножение эпюр (рис. 70) и (рис. 71):

Полученное значение мало по сравнению со значением EIu_B и может быть принято равным нулю.

Пример 8.

Для рамы (рис. 73) требуется:

1) построить эпюры внутренних усилий, используя метод сил;

2) выполнить деформационную проверку.

Жесткости горизонтальных стержней - 2EI, вертикальных - 3EI.

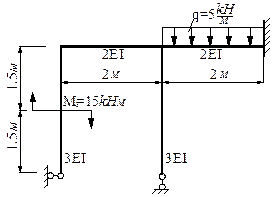
Рис. 73

Решение.

Определим степень статической неопределимости. Рама имеет пять связей, в то время как три связи обеспечивают равновесие плоской системы. Значит, рама дважды статически неопределима.

Образуем основную систему (рис. 74, а). Основная система статически определима и геометрически неизменяема. Приложив к ней внешнюю нагрузку и неизвестные усилия в «лишних» связях Х₁, Х₂ получим эквивалентную систему (рис.74, б).

Запишем канонические уравнения метода сил для дважды статически неопределимой системы:

Построим эпюру изгибающих моментов от внешних сил

Эпюра M_F дана на (рис.74, г)

Построим эпюры изгибающих моментов ( и ) от единичных сил по направлению усилий X₁, X₂ (рис. 74, д, е).

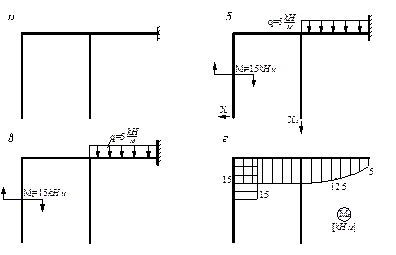
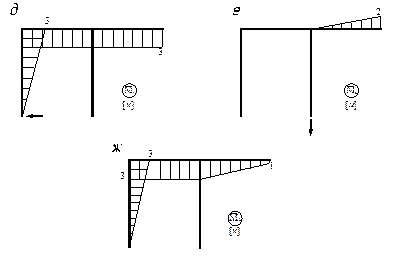
Рис. 74

Определим коэффициенты канонических уравнений по правилу Верещагина:

Для проверки единичных коэффициентов построим суммарную единичную эпюру M_S (рис. 74, ж) путем сложения ординат эпюр и и «перемножим» ее саму на себя:

Полученный результат должен быть равен сумме «единичных» коэффициентов

Для проверки «грузовых» коэффициентов перемножим грузовую M_F и суммарную единичную M_S эпюры:

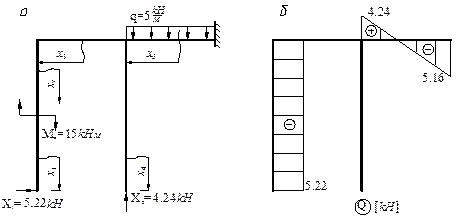
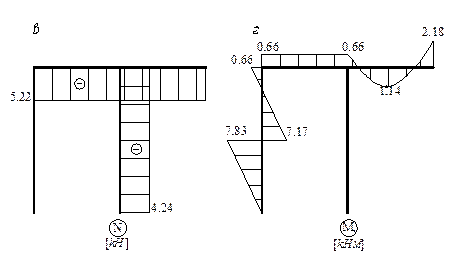
Рис. 75

Сумма грузовых коэффициентов равна той же величине:

Совпадение результатов говорит о правильности расчетов.

Подставим значения коэффициентов в канонические уравнения и сократим на общий множитель

Решив систему уравнений, получим: X₁=-5,25 кН; X₂=-4,34 кН.

Знаки «минус», свидетельствуют о том, что принятые направления Х₁ и Х₂ следует изменить на противоположные.

Строим эпюры внутренних усилий N, Q, M (рис.75, б, в, г) с учетом найденных значений Х₁ и Х₂, используя метод сечений. Так, для наиболее сложного пятого участка имеем:

0≤x₅≤2 м.

N_V= -X₁ = -5,25 кН;

Q_V=X₂ - qx₅

при x₅ = 0: Q_V= 4,24 кН.

при x₅ = 2 м: Q_V= -5,76 кН.

M_V = -X₁∙3 + M_e + X₂∙x₅ – qx₅2/2

при x₅ = 0: M_V= -0,66 кНм.

при x₅ = 2 м: Q_V= -2,18 кНм.

Определим экстремум

Q_V=X₂ - qx₅ =0 → x₅=4,24/5 = 0,848 м.

M_V = -X₁∙3 + M_e + X₂∙0,848 – q∙0,8482/2 = 1,11 кНм.

Деформационная проверка правильности найденных значений неизвестных Х₁ и Х₂ состоит в том, что мы определяем перемещение в направлении какой либо связи (Х₂), «перемножив» эпюру M (рис. 75, г) и (рис. 74, е), заранее зная, что это перемещение должны быть равным нулю.

Пример 9.

Статически неопределимая рама (рис.76) с постоянной жесткостью вертикальных и горизонтальных элементов, имеющая размеры l=4 м и h=6 м нагружена в своей плоскости распределенной нагрузкой q=11 кН/м.

Требуется:

1) установить степень статической неопределимости;

2) выбрать основную систему;

3) составить канонические уравнения;

4) Построить эпюры М от единичных сил и от заданной нагрузки;

5) Вычислить коэффициенты и свободные члены канонических уравнений, проверить их, решить систему и найти величины лишних неизвестных;

6) Построить расчетные эпюры М, Q и N;

7) Выполнить статическую проверку узлов.

Рис.76

Решение.

1. Степень статической неопределимости системы определяется равенством s = n – 3, где 3 – число независимых уравнений статики, которые можно составить для плоской системы сил; n – число связей, наложенных на раму. В нашем случае 3 связи дает жесткая заделка и по 1 связи дают катки. Итого n=5. Значит степень неопределимости системы равна: s=n-3=5-3=2

2) Для составления канонических уравнений выберем основную и эквивалентную систему отбросив катки и заменим их реакциями X₁ и X₂ (рис.77).

Рис.77

3) Составляем систему канонических уравнений

4) Строим эпюры моментов от единичных сил X₁=1 и X₂=1 и заданной нагрузки (рис.78):

Рис.78

5) вычисляем коэффициенты и свободные члены канонических уравнений.

Решаем систему канонических уравнений:

Подставим значения:

Или:

Решим уравнения:

Домножим первое уравнение на 2.5.

Вычтем из второго уравнения первое:

Откуда:

Подставим полученное значение в первое уравнение

откуда

Найдем недостающие опорные реакции из эквивалентной системы (рис.79):

Рис.79

Откуда:

откуда

Строим эпюры N, Q, и M (рис.80).

Рис.80

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00